supriyag

Complementary Angles Supplementary Angles And Adjacent Angles

It is seen that the sum of ∠A and ∠E is 90° or one right angle. What can be termed such two angles?

If the sum of measurement of 2 angles is 90°, then they are called complementary angles to each other. Here the complementary angle of ∠A is ∠E and vice-versa. I got ∠E is the complementary angle ∠A ∠B [∠C /∠D]

“WBBSE Class 8 Maths Chapter 6 solutions, Complementary Angles Supplementary Angles and Adjacent Angles”

Which pair among ∠H, ∠I and ∠L form complementary angles?

∠H and ∠I are complementary, and ∠l and ∠L are complementary to each other.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

Now I write the measurement of the supplementary angle of ∠G and draw it with a protractor.

The supplementary angle of ∠G is = 180° – 118° – 62°

Read and Learn More WBBSE Solutions For Class 8 Maths

Complementary Angles Exercise

Question 1. Let’s find which pair of angles are complementary or supplementary among the following pairs of angles and then draw.

Solution:

10°, 170°; 38°, 52°; 35°, 65°; x90°, 90°; 25°, 165°; 45°, 45°

10°, 170° supplementary

90°, 90° supplementary

45°, 45° complementary

38°, 52° complementary

∠ABC and ∠CBD are supplementary angles.

∠MNO and ∠MNP supplementary.

“Class 8 WBBSE Maths Chapter 6 solutions, Complementary and Supplementary Angles explained”

∠WXY and ∠YXZ are supplementary angles.

∠PQR and ∠RQS are supplementary angles.

New we think whether are 1,2 are 4 ∠A and ∠B are adjacent angles.

In figures 2 and 3 one side of ∠A and ∠B aren’t complementary but in figure one side ∠A and ∠B is (ordinary) but on one side of there are two angles.

In figure, 3 the origin of both angles isn’t same.

In figure 4  both angles are adjacent angles because origin of both is same and on both sides, there are ∠A and ∠B.

Here we measure both [a] and \b\ are complementary angles. If ∠A = 65°, ∠B = 115°; then ∠A + ∠B = 180° degrees.

Now we see both adjacent angles ∠A and ∠B. are ∠A = 65 degrees. ∠B = 115 degrees and ∠A + ∠B = 180 degrees. My brother kept a pen in the pen-stand as is shown in the picture. We see that two adjacent angles adjacent ∠A and ∠B are formed. Measuring we get ∠A + ∠B = 180 degrees.

It is seen by measuring adjacent angles that ∠PQY= 45°, ∠PQX = 135° and ∠PQY + ∠PQX = 180° and ∠MND = 130°, ∠MNC = 50° and ∠MND + ∠MNC= 180°

It one ray is inclined on a straight line then two adjacent angles are formed. The sum of the measurement of them is equal to two right angles right angle or M 180 degrees.

Complementary Angles Exercise

Question 1. Let’s write the sum of measurements of which adjacent angles are two right angles in the figures below.

Solution:

Question 2. Let’s draw a straight line AB and consider a point P on the line AB. Let’s erect a ray from P on the straight line AB. As a result, two adjacent angles are formed. Now we measure the adjacent angles and examine whether the sum of the measurement of those angles is 180° or not.

Solution:

On the line AB from the point P we draw a straight line, so are formed two adjacent angles ∠QPA and ∠QPB.

∠QPA = 60°, ∠QPB – 120°

The sum of the angles is = 60° + 120° = 180° or two right angles.

“WBBSE Class 8 Maths Chapter 6, Complementary Angles and Adjacent Angles solved examples”

Now we will play a game with the help of three colourful sticks. We will form two angles whose sum total is 180° or 2 right angles joining one end of these colourful sticks. I formed

By stick ∠A and ∠B are termed.

∠A = 113°and ∠B = 67° ∠A + ∠B = 180 degree

The common side of two adjacent angles ∠A & ∠B is Green coloured stick. It is seen by drawing on the exercise book that two uncommon sides of two adjacent angles ∠A and ∠B, i.e., the red and the blue sticks lie on a straight line.

Zakir formed

Formed by sticks where ∠A = 70°, ∠B = 110°.

Here the common side of ∠A and ∠B is the green coloured stick.

It is seen by drawing on an exercise book that two uncommon sides of two adjacent angles ∠A ∠B, i.e., the red and the blue sticks lie on a straight line.

Julefa drew some angles in her exercise book and measured them with a protractor. She marked the angles.

Siraj will take two such angles from the angles drawn by Julefa, the sum of which is 180°or two right angles. Then he will see that the two exterior arms are in the same straight line.

“WBBSE Class 8 Complementary Angles Supplementary Angles solutions, Maths Chapter 6”

At first, I took ∠ABC = 80°. New I took the supplementary 100 degrees or angle of ∠XYZ. Now I placed side AB of ∠ABC or the side XY of ∠XYZ.

It is seen that segments YZ and BE lie on the same straight line BC. Similarly, I placed the supplementary angle of 155 degrees of 25° as the figure beside.

It is seen that two line segments KL and EF lie on the same straight line.

∠PQR. Let’s draw adjacent angles with the angles whose measurements are given below and examine whether the external sides of those adjacent angles lie on a same straight line or not.

∠PQR = 85°. Its supplementary angle is ∠PQS = 95°. It’s external arms QR and QS lie on the straight line.

I got if the sum of measurement of two adjacent angles is 180° or 2 right angles, their external sides lie on a same straight line.

“Class 8 WBBSE Maths Chapter 6, Complementary Angles easy explanation”

Let’s draw adjacent angles with the angles, whose measurements are given below and examine whether the external sides of those adjacent angles lie on a same straight line or not.

1. 37°, 113°
2. 41°, 139°
3. 94°, 86°
4. 90°, 90°

Question 1. Let’s think and write :

1. Whether two complementary angles are acute to each other or not.

Solution:

Two acute angles can be complementary two each other.

2. Whether two acute angles are supplementary to each other or not.

Solution:

Two acute angles cannot be supplementary to each other.

3. Let’s write whether one acute angle and one obtuse angle are complementary to each other. Also, examine whether two right angles are complementary to each other or not.

Solution:

One acute angle and one obtuse angle and two right angles cannot be complementary to each other.

4. Let’s write whether two obtuse angles are supplementary to each other or not.

Solution:

Two obtuse angles are not supplementary to each other.

5. Let’s write whether two right angles are supplementary to each other or not.

Solution:

Two right angles are not supplementary to each other.

6. Let’s write whether one acute angle and and obtuse angle are supplementary to each other or not.

Solution:

One acute angle and one obtuse angle can be supplementary to each other.

“WBBSE Class 8 Maths Chapter 6 solutions, Supplementary Angles and Adjacent Angles PDF”

7. Whether two adjacent angles are complementary to each other.

Solution:

Whether two adjacent angles can be complementary to each other.

8. Two adjacent angles are supplementary to each other.

Solution:

Two adjacent angles can be supplementary to each other.

Question 2. Let’s draw adjacent angles with angles whose measurements are given below and examine which pair of angles are complementary to each other:

Solution:

Given

45°,45°,120°,30°,110°;42°,48°,37°,43°,85°,95°;

45°,45° – Complementary angles

70°, 110° – Supplementary angles

48°, 42° – Complementary angles

95°, 85° – Supplementary anglers

Question 3. Let’s see the measurement of the angles given below and examine which pair of angles are complementary to each other: 31°,47°,64°,29°,43°,59°,17°,26°

Solution:

Given

31°,47°,64°,29°,43°,59°,17°,26°

47° and 43° – Complementary angles

64° and 26° – Complementary angles

31° and 59° – Complementary angles

“WBBSE Class 8 Maths Chapter 6, Complementary and Supplementary Angles important questions”

Question 4. Let’s see the measurement of the angles given below and examine which pair of angles are supplementary to each other:

Solution:

47°,58°,69°,75°,133°,105°,122°,125°

47° and 133° – Supplementary angles

58° and 122° – Supplementary angles

Question 5. Let’s define adjacent angles and write which pair of angles are adjacent from the following figures :

Solution:

When two angles have a common arm, origin and both angles are on either common arm, those angles are called adjacent angles. In first and third figures  ∠A and ∠B are adjacent angles.

Question 6. Let’s draw adjacent angles by protractor whose measurements are given below :

Solution:

35°,45°,18°,42°,32°,90°,73°,63°

∠ABC + ∠CBD = 35° + 45° = 80°

∠PQR + ∠RQS = 18° -4- 42° = 60°

∠XO Y + ∠YOZ = 32° + 90° =122°

∠MON + ∠NOR = 73° + 63° = 136°

Question 7. Sayantani drew a straight line AB. I erected a ray PQ from a point P on AB. As a result, two adjacent angles ∠PQB and ∠PQA are formed. Let’s write the measurement of ∠PQB and ∠PQA and ∠PQB + ∠PQA by using protractor.

Solution:

Given

Sayantani drew a straight line AB. I erected a ray PQ from a point P on AB. As a result, two adjacent angles ∠PQB and ∠PQA are formed.

Question 8. Shakil draws two adjacent angles ∠ABC and ∠ABD whose sum of measurements is 180°; I also drew ∠ABC and ∠ABD like Shakil and examined whether points D, B and C lie on a same straight line or not.

Solution:

Given

Shakil draws two adjacent angles ∠ABC and ∠ABD whose sum of measurements is 180°; I also drew ∠ABC and ∠ABD like Shakil

 

Question 9. ∠ABC and ∠ABD are formed whose sum is 180°. We see that D, B and C lie on a same straight line.

Solution:

Given

∠ABC and ∠ABD are formed whose sum is 180°.

Let’s find the value of X from the figure beside.

∠AOD + ∠DOC+ ∠COB=180C

or, 3x° + 80° + x° = 180°

or, 4x° = 180° – 80°

or, 4x° = 100°

= \(x^{\circ}=\frac{100^{\circ}}{4}=25^{\circ}\)

The value of  \(x^{\circ}=\frac{100^{\circ}}{4}=25^{\circ}\)

“Class 8 Maths Complementary and Supplementary Angles solutions, WBBSE syllabus”

Question 10. From the figure if ∠AOP, ∠BOP are greater than 140°, then find the value of ∠AOP and ∠BOP.

Solution:

Given

From the figure if ∠AOP, ∠BOP are greater than 140°,

Let ∠BOP = x°

∠AOP = x° + 140°

∵ ∠AOP + ∠BOP = 180°

∴ x° + 140° + x° = 180°

or, 2x° = 180° – 140°

or, 2x° = 40°

or, x° = \(\frac{40^{\circ}}{2}\)

or, x° = 20°

∴ ∠BOP – 20° ∠AOP = 20° + 140° = 160°

Question 11. Measurement of two adjacent angles are 35°-and 145°. Let’s write how the external! sides of those two angles are situated.

Solution:

Given

Measurement of two adjacent angles are 35°-and 145°.

= 35° + 145° = 180°

∴ Both external sides of the adjacent angles lie on a same straight line.

Question 12. From the figure OA and OE line segments are situated in which manner?

Solution:

 

∠AOB+ ∠BOC + ∠COD+ ∠DOE

= 20° + 55° + 81°+24°

= 180°

∠AOB+ ∠BOC + ∠COD+ ∠DOE = 180°

∴ OA and OE are situated on a sama straight line.

Cubes

Today Sundy and Firoz are making many colourful boxes.

Measuring we see that the length of the box is 1 cm, breadth is 1 cm and height is 1 cm, i.e., each of these boxes is cubical.

Length of each side of this cubical box is 1 cm.

But to make a cubical box of side 3 cm in length,27 small boxes are required.

What shall we call such numbers like 1, 8, 27,?

1,8, 27 are called perfect cube numbers because 1 = (1)3, 8

= (2)³, 27 = 3³, 8 = 2³, 64 = 4³, 125 = 5³, .

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

i.e., cubes of 1,2, 3, 4, 5, are respectively 1, 8, 27, 64, 125,…

I try to make a cube with 32 cubes of same size:

32 = 2×2×2×2×2

= (2 × 2) x (2 × 2) × 2

= 4×4×4, i.e., 32 ≠ (any integer)3

Read and Learn More WBBSE Solutions For Class 8 Maths

We see, it not possible to make a bic, cube with 32 small cubes. But it is possible to make a big cube with 32×2=64 small cubes. So, 64 is a perfect cube number, i.e., 32 is not a perfect cube number but we get a perfect cube number by multiplying 32 with the smallest positive integer 2 because 64 = 4³

Let’s see whether Tatai can make a big cube with 54 small cubes of the same size as above.

54 = 2×3×3×3

We see 54 is a not-perfect cube number (Perfect cube no. / not perfect cube number.)

∴  Is 54? If we divide by the smallest positive integer then we will get perfect cube number. So, 54÷2 = 27 a not perfect cube number Because 27 = 3³.

Cubes Exercise

Question 1. Let’s find perfect cube from the following numbers: 125, 500, 64, 73, 729, 968.

Solution:

Given

125, 500, 64, 73, 729, 968.

125 = 5³, 64 = 4⁴, 73, 729 = 9³

Let’s write perfect cubes in the chart below, making cube from 1 to 20.

See the term from the above chart 9 = 1³ + 2³, 280= 4³+ 6³, 1729 = 10³+ 10³(Let’s make another).

Firoz made many big cubes attaching these small cubes. Suhana and I are measuring the length of each side of cube.

There are 27 small cubes in this big cube.

See, the length of each side of big cube beside the picture is 3 cm. I got differently 27 = 3³

What can be termed 3 of 27?

Cubing 3, we get 27.

So the cube root of 27 is 3.

125= 5×5×5=5³

“WBBSE Class 8 Maths Chapter 5 solutions, Cubes”

∴ \(\sqrt[3]{125}\) = 5

729 = 3×3×3×3×3×3

= 3³+3³

∴ \(\sqrt[3]{729}\) = 3×3=9

Cubes Exercise

Question 1. Let’s form two cubes with sides of length 5 cm and 1 cm. Let us calculate the number of small cubes to form the big cube.

Solution:

Given

Sides of length 5 cm and 1 cm.

Number of small cubes required to make this big cube = (5)³ = 5 × 5 × 5 = 125

Question 2. Sumanta has made many cubes of 1 cm length. Manami is trying to make big cubes attaching these small cubes. Let’s see in which of the cube given below Manami will be able to make big cubes.

1. 100

Solution:

Given

100 = 2 × 2 × 5 × 5 = 2² × 5²

2. 1000

Solution:

Given

1000 = 10 × 10 × 10 = (10)³

∴ \(\sqrt[3]{1000}\) = 10

“Class 8 WBBSE Maths Chapter 5 solutions, Cubes study material”

3. 1331

Solution:

Given

1331 = 11×11×11= (11)³

∴ \(\sqrt[3]{1331}\)=11

4. 324

Solution:

Given

324 = 2×2×3×3×3×3 = (2)² × (3)² × (3)²

5. 3375.

Solution:

Given

3375 = 15×15×15 = (15)³

∴ \(\sqrt[3]{3375}\) = 15

6. 1372

Solution:

Given

1372 = 2×2×7×7×7 = 2^2×7³

Question 2. Manami can make a big cube by attaching the following number of small cubes :

Solution:

• 1000,
• 1331
• 3375

Question 3. Let us write number which is not a perfect cube in the numbers given below :

1. 216

Solution:

Given

216 = 2 x 2 x 2 x 3 x 3 x 3

= 2³ x 3³

= 6³

216 = 6³

2. 343

Solution:

Given

343 = 7 x 7 x 7

= 7³

343 = 7³

3. 1024

Solution:

Given

1024 =2×2×2×2×2×2×2×2×2×2

= 2³×2³×2³×2

= 8³×2

1024 = 8³×2

4. 324

Solution:

Given

324 = 2×2×3×3×3×3

= 2³ × 3³ × 3

324 = 2³ × 3³ × 3

“WBBSE Class 8 Maths Chapter 5, Cubes solved examples”

5. 1744

Solution:

Given

1744 = 2 × 2 × 2 × 2 × 109

= 2³×2 ×109

1744 = 2³×2 ×109

6. 1372

Solution:

Given

1372 = 2 × 2 × 7 × 7 × 7

= 2² × 7³

1372 = 2² × 7³

The following aren’t perfect cube numbers :

• 1024,
• 324,
• 1744 and
• 1372

Question 4. Dabnath has made a cuboid whose length, breadth, and height are respectively 4 cm, 3 cm, and 3 cm. Let’s see how many cuboids of this type will form a cube.

Solution:

Given

Dabnath has made a cuboid whose length, breadth, and height are respectively 4 cm, 3 cm, and 3 cm.

Length of the cuboid = 4 cm

Breadth = 3 cm.

Height = 3 cm

∴  Number of cuboids required to make the cube = 4×3×3 = 36

Question 5. Let us calculate with which positive smallest number should be multiplied by the numbers below so that the product will be a perfect cube.

1. 675

Solution:

Given

675 = 3 ×3 × 3 × 5 × 5 = 3³ × 5²

∴  675 is not a perfect cube number.

But, 3³ ×5² × 5 = 3³ × 5³ = (15)³

= 3375

Multiplying 675 by the smallest positive number 5, the product 3375 will be a perfect cube number.

2. 200

Solution:

Given

200 = 2×2×2×5×5 = 2³×5²

∴ 200 is not a perfect cube number.

But, 2³×5²×5 = 23×5³=(10)³ = 1000

Multiplying 200 by the smallest positive number 5, the product 1000, will be a perfect cube number.

3.108

Solution:

Given

108 = 3 × 3 × 3 × 2 × 2 = 3³ × 2²

∴ 108 is not a perfect cube number.

But, 3³ × 2²×2

= 3³ × 2³

= (6)³

= 216

∴  Multiplying 108 by the smallest positive number 2, the product 216 will be a perfect cube number.

“WBBSE Class 8 Cubes solutions, Maths Chapter 5”

4. 121.

Solution:

Given

121 = 11 ×11 = (11)²

∴ 121 is not a perfect cube number

But, (11)² × 11 = (11)³ = 1331

∴ Multiplying 121 by the smallest positive number 11, the product 1331 will be & perfect cube number.

5. 1225

Solution:

Given

1225 = 5×5×7×7 = 5²×7²

∴  1225 is not a perfect cube number

But, 5² × 7² × 5 × 7

= 5³ × 7³

= (35)³

= 42875

∴ Multiplying 1225 by the smallest positive number 35, the product 42875 will be a perfect cube number.

Question 6. Let us calculate with which positive smallest number should the number be divided so that the quotient will be a perfect cube.

1. 7000

Solution:

Given

7000 = 7 × 10 × 10 × 10 = 7 × (10)³

∴ Dividing 7000 by the smallest positive number 7, the quotient will be a perfect cube number.

∴ Required number = 7

2. 2662

Solution:

Given

2662 = 2×11 × 11 × 11 = 2 × (11)³

∴ Dividing 2662 by the smallest positive number 2, the quotient will be a perfect cube number.

∴ Required number = 2

3. 4394

Solution:

Given

4394 = 2 × 13 × 13 × 13 = 2 × (13)³

Dividing 4394 by the smallest positive number 2, the quotient will be a perfect cube number.

Required number = 2

4. 6750

Solution:

Given

6750 = 2 × 3 × 3 × 3 × 5 × 5 × 5 = 2 × 3³ × 5³

Dividing 6750 by the smallest positive number 2, the quotient will be a perfect cube number.

Required number = 2

“Class 8 WBBSE Maths Chapter 5, Cubes easy explanation”

5. 675

Solution:

Given

675 = 3×3×3×5×5 = 3³×5²

Dividing 675 by the smallest positive number 25, the quotient will be a perfect cube number.

Required number = 25

Question 7. Let us write the number below as product of prime factors and write the cube roots of the numbers.

1. 512

Solution:

Given

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2

The cube root of 512

= 2³ × 2³ × 2³ = 8³

∴ \(\sqrt[3]{512}\) = 8

The cube root of 512 = 8

2. 1728

Solution:

Given

1728 = 2×2×2×2×2×2×3×3×3

= 2³×2³×3³

=(12)³

∴ \(\sqrt[3]{1728}\)= 12

The cube root of 1728 = 12

3. 5832

Solution:

Given

5832 = 2×2×2×3×3×3×3×3×3

= 2³× 3³×3³=(18)³

∴ \(\sqrt[3]{5832}\)= 18

The cube root of 5832 = 18

4. 15625

Solution:

Given

15625 = 5×5×5×5×5×5

= 5³×5³ = (25)³

∴ \(\sqrt[3]{15625}\) = 25

The cube root of 15625 = 25

5. 10648

Solution:

Given

10648 = 2×2×2×11×11×11

= 2³× 11³= (22)³

∴ \(\sqrt[3]{10648}\) = 2

After measuring we see that the length of a side of this cubical box is 12 cm. ‘

∴ Volume = 12³ cc. = 1728 cc.

Question 8. If the length of a side of the cubical box was x cm, then the volume was = (x cm)³ = x³ cc. If the length of a side of the cubical box was (x + 2) cm, then the volume of the box was = (x + 2)³ cm.

Solution:

Given

If the length of a side of the cubical box was x cm, then the volume was = (x cm)³ = x³ cc. If the length of a side of the cubical box was (x + 2) cm, then the volume of the box was = (x + 2)³ cm

Let us see what we get after expanding (x + 2)³.

(x + 2)³ = (x + 2) x (x + 2)²

= (x + 2) {x² + 4x + 4} [with the help of identity (a + b)² = a² + 2ab + b²]

= (x + 2) x² + (x + 2) 4x + (x + 2) 4 [with the help of Distributive Law]

= x³+ 2x² + 4×2+ 8x + 4x + 8 [with the help of associative] law]

= x³+ 6x² + 12x + 8

Titli wrote the length of a side of this cube as (a + b) cm.

∴ The volume of this cube is (a + b)³ cc.

= (a + b)³ = (a + b) (a + b)²

= (a + b) × a² + 2ab + b2

= (a + b) x a² + (a + b) 2ab + (a + b) b² [Distributive Law]

= a³ + b²a + 2a²b + 2ab² + ab² + b³ [Distributive Law]

= a³ + ab² + 2a²b + 2ab² + ab² + b³ [b²a = ab², by commutative Law of Multiplication.]

= a³ + 3a²b + 3ab² + b3

We get (a + b)³ = a³ + 3a²b + 3ab² + b³

(a + b)³ = a³ + 3a²b + 3ab² + b³

= a³ + 3ab (a + b) + b³

We got with the help of commutative & distributive laws (a + b)³ = a³+ b³ + 3ab (a + b)

1. (2y + 3)³ (Let’s expand).

Solution:

Given (2y + 3)³

= (2y)³ + 3 (2y)³ 3 + 3.2y. (3)³ + (3)³ there a =2y b = 3

(2y + 3)³ = (2y)³ + 3 (2y)³ 3 + 3.2y. (3)³ + (3)³

2. (15)³

Solution:

Given (15)³

= (10+5)³

= 3375

(15)³ = 3375

3. (101)³

Solution:

Given (101)³

= (100+1)

= (100+1)

= 1030301

(101)³ = 1030301

“WBBSE Class 8 Maths Chapter 5 solutions, Cubes PDF”

4. (210)

Solution:

Given (210)

= (200+10)³

= 9261000

(210) = 9261000

5. If the length of one side of the cube is = (a – b) cm, we get,

Solution:

The volume of the cube = (a – b)³ cc

(a – b)³ Let’s see by expanding

(a – b)³ = {a + (- b)}³ = a³ + 3 (a²) (-b) + 3a (-b)² + (-b)³

(a – b)³ = a³ – 3a³b + 3ab² – b³

With the help of identity no.3, I expand

6. (99)³ and find the value of it.

Solution:

Given (99)³

= (100 – 1)³

= (100)³ – 3 (100)2 x 1 + 3 x 100 x (1 )2 – (1 )³

= 970299

(99)³ = 970299

Question 9. If x – \(\frac{1}{9 x}\)= 1 then find the value of 27×3 – \(\frac{1}{27 x^3}\)

Solution:

= \(x-\frac{1}{9 x}=1\)

or, \(3\left(x-\frac{1}{9 x}\right)\) = 1×3(Multiplying both sides by 3)

or,\(3 x-\frac{1}{3 x}\) = 3

or,\(\left(3 x-\frac{1}{3 x}\right)^3\) = 3 (Cubing both sides)

or,\(27 x^3-\frac{1}{27 x^3}-3 \times 3 x \times \frac{1}{3 x}\left(3 x-\frac{1}{3 x}\right)\) = 27

or,\(27 x^3-\frac{1}{27 y^3}-3 \times 3\) = 27

∴ \(27 x^3-\frac{1}{27 x^3}\) = 36

Question 10. Let us solve the questions below with the help of identities from I to IV.

1.  If x – y = 2 then find the value of x³ – y³ – 6xy.

Solution:

Given x – y = 2

x³ – y³ – 6xy = x³ – y³ – 3xy.2 = x³ – y³ – 3xy (x – y)

= (x – y)³.

= (2)³

= 8

The value of x³ – y³ – 6xy = 8

2. If a + b = – -then prove that a³+ b³ – ab = \((a+b)^3-3 a b(a+b)-a b\)

Solution:

Given a³+ b³ – ab = \((a+b)^3-3 a b(a+b)-a b\)

L.H.S. = a³ + b³ – ab .

= (a + b)³ – 3ab (a + b) – ab

a³+ b³ – ab = (a + b)³ – 3ab (a + b) – ab

= R.H.S. Proved

3. If x + y = 2 and \(\frac{1}{x}+\frac{1}{y}=2\) then find the value of x³ + y³.

Solution:

Given

x + y = 2 and \(\frac{1}{x}+\frac{1}{y}=2\)

= \(\frac{1}{x}+\frac{1}{y}=2\)

= \(\frac{y+x}{x y}\) =2

= \(\frac{x+y}{x y}\) = 2

or, \(\frac{2}{x y}\)= 2

or, xy = 1

= x³ + y³

= (x + y)³ – 3xy (x + y)

= (2)³ – 3×1 x 2

= 8-6

= 2

The value of x³ + y³ = 2

4. If \(\frac{x^2-1}{x}\) = 2 then find the value of \(\frac{x^6-1}{x^3}\)

Solution:

Given

\(\frac{x^2-1}{x}\) = 2

= \(\frac{x^2-1}{x}=2\)

or, \(\frac{x^2}{x}-\frac{1}{x}=2\)

or,\(x-\frac{1}{x}=2\)

∴ \(\frac{x^6-1}{x^3}\)

= \(\frac{x^6}{x^3}-\frac{1}{x^3}\)

= \(x^3-\frac{1}{x^3}\)

= \((x)^3-\left(\frac{1}{x}\right)^3\)

= \(\left(x-\frac{1}{x}\right)^3+3 \cdot x \cdot \frac{1}{x}\left(x+\frac{1}{x}\right)\)

= (2)³ + 3x²

= 8 + 6

= 14

The value of \(\frac{x^6-1}{x^3}\) = 14

“WBBSE Class 8 Maths Chapter 5, Cubes important questions”

5.  If x + \(\frac{1}{x}\) = 5 then find the value of x³ + \(\frac{1}{x^3}\)

Solution:

Given

x + \(\frac{1}{x}\) = 5

= \(x+\frac{1}{x}=5\)

= \(x^3+\frac{1}{x^3}\)

= \((x)^3+\left(\frac{1}{x}\right)^3\)

= \(\left(x+\frac{1}{x}\right)^3-3 \cdot x \cdot \frac{1}{x}\left(x-\frac{1}{x}\right)\)

= (5)³-3×5

= 125-15

=110

The value of x³ + \(\frac{1}{x^3}\) =110

6. If x = y + z then find the value of x³– y³– 3xyz.

Solution:

Given

x = y + z

= x – y = z

= (x – y)³ = (z)³ (Cubing both sides)

= x³– y³– 3xy (x – y) = z³

= x³– y³ – 3xy.z = z³ (∴x – y = z)

= x³– y³ – 3xy.z=0

The value of x³– y³– 3xyz =0

“Class 8 Maths Cubes solutions, WBBSE syllabus”

7. If xy ( x + y) = m then prove that x³+ y³+ 3m =\(\frac{m^3}{x^3 y^3}\)

Solution:

Given xy ( x + y) = m

xy ( x + y) = m

= x + y=\(\frac{m}{x y}[latex]

= [latex](x+y)^3=\left(\frac{m}{x y}\right)^3\)

= \(x^3+y^3+3 x y(x+y)=\frac{m^3}{x^3 y^3}\)

= \(x^3+y^3+3 x y \cdot \frac{m}{x y}=\frac{m^3}{x^3 y^3}\)

= \(x^3+y^3+3 m=\frac{m^3}{x^3 y^3}\)

Proved.

8. If 2x + \(\frac{1}{3 x}\) = 4 then prove that 27x³ + \(\frac{1}{8 x^3}\) = 189.

Solution:

Given

2x + \(\frac{1}{3 x}\) = 4

= \(2 x+\frac{1}{3 x}=4\)

= \(\frac{3}{2}\left(2 x+\frac{1}{3 x}\right)=\frac{3}{2} \times 4\)(Multiplying sides by \(\frac{3}{2}\)

= \(3 x+\frac{1}{2 x}=6\)

= \(\left(3 x+\frac{1}{2 x}\right)^3=(6)^3\)(Cubing both sides)

= \((3 x)^3+\left(\frac{1}{2 x}\right)^3+3.3 x \frac{1}{2 x}\left(3 x+\frac{1}{2 x}\right)=216\)

= \(27 x^3 \frac{1}{8 x^3}+\frac{9}{2} x 6=216\)

= \(27 x^3+\frac{1}{8 x^3}=216-27\)

= \(27 x^3+\frac{1}{8 x^3}=189\)

Proved.

9. If 2a-\(\frac{2}{a}\)+1=0 then find the value of \(a^3-\frac{1}{a^3}+2\)

Solution:

Given

2a-\(\frac{2}{a}\)+1=0

= \(2 a-\frac{2}{a}+1=0\)

or, \(2\left(a-\frac{1}{a}\right)=-1\)

or, \(a-\frac{1}{a}=-\frac{1}{2}\)

∴ \(a^3-\frac{1}{a^3}+2\)

= \((a)^3-\left(\frac{1}{a}\right)^3+2\)

= \(\left(a-\frac{1}{a}\right)^3+3 \cdot a \cdot \frac{1}{a}\left(a-\frac{1}{a}\right)+2\)

= \(\left(-\frac{1}{2}\right)^3+3\left(-\frac{1}{2}\right)+2\)

= \(\left(-\frac{1}{2}\right)^3+3\left(-\frac{1}{2}\right)+2\)

= \(-\frac{1}{8}-\frac{3}{2}+2\)

= \(\frac{-1-12+16}{8}\)

= \(\frac{3}{8}\)

The value of \(a^3-\frac{1}{a^3}+2\) = \(\frac{3}{8}\)

10. a³+b³+c³ = 3abc then find the value of (a+b+c). Given (a≠b≠c).

Solution:

Given a³+b³+c³ = 3abc

or, (a+b)³-3ab(a+b)+c³=3abc

or, (a+b)³+c³-3ab(a+b)-3abc=0

or, (a+b+c){(a+b)²-(a+b)c+(c)²}=0

or, (a+b+c) (a²+2ab+b²-ac-bc+c²-3ab)=0

or, (a+b+c) (a²+b²+c²-ab-ac-ac)=0

∵ The product of both expressions is zero.

∵ At least one of the expressions is zero.

∵ Here a≠b≠c

∵ a+b+c=0

The value of (a+b+c) =0

11. If m+n=5 and mn=6 then find the value of (m²+n²)(m³+n³).

Solution:

Given m+n=5 and mn= 6

(m²+n²) (m³+n³)

= {(m+n)-2mn}{(m+n)³-3mn(m+n)}

= {(5)²-2×6}{(5)³-3×6×5}

= (25-12) (125-90)

= 13×35

= 455

The value of (m²+n²)(m³+n³) = 455

Question 11. Let’s multiply with the help of identity no.5

1. (7 + 3x) (49 – 21 x + 9x²)

Solution:

Given (7 + 3x) (49 – 21 x + 9x²)

= (7 + 3x) (49 – 21 x + 9x²)

= (7 + 3x) {(7)² – 7 x 3x + (3x)²}

= (7)³ + (3x)³

= 343 + 27x³

(7 + 3x) (49 – 21 x + 9x²) = 343 + 27x³

2. (x² + y²) (x⁴ – x²y² + y⁴)

Solution:

Given (x² + y²) (x⁴ – x²y² + y⁴)

(x²+y²){(x²)²-x²y²+(y²)²}

= (x²)³+(y²)³

= x⁶+y⁶

(x² + y²) (x⁴ – x²y² + y⁴) = x⁶+y⁶

Question 12. Let’s try to factorize the following algebraic expression with the help of identity no. V

1. p³q³ + 1

Solution:

Given p³q³ + 1

= p³q³ + 1

= (pq)³ + (1)³

= pq+1×p²q²-pq+1

p³q³ + 1 = pq+1×p²q²-pq+1

Question 13. Let’s find the product of the following algebraic expression with the help of identity no. VI

1. (p – 2q) (p² + 2pq + 4q²)

Solution:

Given (p – 2q) (p² + 2pq + 4q²)

= (p – 2q) (p² + 2pq + 4q²)

= (P – 2q) {p²+ p x 2q + (2q)²}

= (p)³ – (2q)³ [ By identity no. V ]

= (p)³-8q³

(p – 2q) (p² + 2pq + 4q²) = (p)³-8q³

2. (x² – 1) (x⁴ + x² + 1)

Solution:

Given (x² – 1) (x⁴ + x² + 1)

= (x² – 1) {(x²)² + x² x 1 + 1²}

= ((x²)³-(1)³)

= x⁶-1

(x² – 1) (x⁴ + x² + 1) = x⁶-1

3. 2x {(4x – 3)2 + (4x – 3) (2x – 3) + (2x – 3)2}

Solution:

Given 2x {(4x – 3)2 + (4x – 3) (2x – 3) + (2x – 3)2}

= {(4x – 3) – (2x – 3)} {(4x – 3)² + (4x – 3) + (2x – 3)²}

[Since : (4x – 3) – (2x – 3)} = 4x – 3 – 2x + 3 = 2x]

Let 4x – 3 = a and 2x – 3 = b = (a – b) {a² + ab + b²}

= a³ – b³ [ With the help of identity no. VI]

= (4x – 3)³– (2x -3)³ [By replacing a = 4x – 3 and b = 2x – 3]

= {(4x)³ – 3.(4x)² x 3+3.4x.3³-(3)³}-{(2x)³-3(2x)² 3+3 x 2x x 32.3³}

= 64x³ – 144x² + 108x – 27 – {8x³ – 36x² + 54x – 27}

= 56x³ – 108x² + 54x

2x {(4x – 3)2 + (4x – 3) (2x – 3) + (2x – 3)2} = 56x³ – 108x² + 54x

“WBBSE Class 8 Chapter 5 Maths, Cubes step-by-step solutions”

Question 14. Let’s factorize the following algebraic expressions with the help of identity no. VI

1. 64 I³ – 34³

Solution:

Given 64 I³ – 34³

= (4l)³-(7)³

= (4l-7)×(16l2+28l+49)

64 I³ – 34³ = (4l-7)×(16l2+28l+49)

2. (x+2)³-(x-2)³

Solution:

Given (x+2)³-(x-2)³

= {(x + 2) – (x – 2)} {(x + 2)² + (x + 2) (x – 2) + (x – 2)²}

= (x + 2 – x + 2) {x² + 4x + 4 + x² – 4x + 4}

= 4x3x²+4

(x+2)³-(x-2)³ = 4x3x²+4

Question 15. Let’s factorize the following algebraic expressions with the help of identity no. 4

1. 8m³ + 12m²n + 6mn² + 2n³

Solution:

Given 8m³ + 12m²n + 6mn² + 2n³

= (2m)³ + 3(2m)² n+3.2mn² + n³ + n³

= (2m + n)³ + n³

= 2m + 2n x

8m³ + 12m²n + 6mn² + 2n³  = 2m + 2n x

2. a³ – 9b³ + (a + b)³

Solution:

Given a³ – 9b³ + (a + b)³

= a³ – b³ – 8b³ + (a + b)³

= a³ – b³+ x(a + b)³ – (2b)³

= (a – b) (a² + ab + b²)+(a + b – 2b)x{(a + b)² + 2b(a + b)+4b²}

= (a – b) (a² + ab + b² + a² + 2ab + b² – 2ab – 2b² + 4b²}

= (a – b)×(2a²+ab+4b²)

a³+b³=a+b×a²+ab+b²)

a³-b³=(a-b)×(a²-ab+b²)

a³ – 9b³ + (a + b)³ = (a – b)×(2a²+ab+4b²)

Let’s simplify using formula :

1. (a + b) (a – b) (a² + ab + b²) (a² – ab + b²)

Solution:

Given (a + b) (a – b) (a² + ab + b²) (a² – ab + b²)

= (a + b) (a² – ab + b²) (a – b) (a² + ab + b²)

= (a³+b³) (a³-b³)

= (a³)²-(b³)² = a6 – b6

(a + b) (a – b) (a² + ab + b²) (a² – ab + b²) = a⁶ – b⁶

2. (a – 2b) (a² + 2ab + 4b²) (a³ + 8b³)

Solution:

Given (a – 2b) (a² + 2ab + 4b²) (a³ + 8b³)

= (a – 2b) {(a)² + a. 2b + (2b)2} (a³ + 8b³)

= {(a)3 – (2b)³} (a³ + 8b³) = (a³-8b³) (a³ + 8b³)

= (a³)² – (8b³)²

= a6 – 64b6

(a – 2b) (a² + 2ab + 4b²) (a3 + 8b3) = a⁶ – 64b⁶

“WBBSE Maths Class 8 Cubes, Chapter 5 key concepts”

3. (4a² – 9) (4a² – 6a + 9) (4a² + 6a + 9)

Solution:

Given (4a² – 9) (4a² – 6a + 9) (4a² + 6a + 9)

= {(2a)² – (3)²} (4a² – 6a + 9) (4a² + 6a + 9)

= (2a + 3) (2a – 3) (4a² – 6a + 9) (4a² + 6a + 9)

= (2a + 3) {(2a)² – 2a.3 + (3)²} (2a – 3) {(2a)2 + 2a.3 + (3)²}

= {(2a)³ + (3)³} {(2a)³ – (3)³} .

= (8a³ + 27) (8a³ – 27)

= (8a³)² – (27)²

= 64a⁶-729

(4a² – 9) (4a² – 6a + 9) (4a² + 6a + 9) = 64a⁶-729

4. (x-y) (x²+xy+y²) + (y-z) (y²+yz+z²) + (z-x) (z²+zx+x²)

Solution:

Given (x-y) (x²+xy+y²) + (y-z) (y²+yz+z²) + (z-x) (z²+zx+x²)

= x³ – y³ + y³ – z³ + z³ – x³ = 0

(x-y) (x²+xy+y²) + (y-z) (y²+yz+z²) + (z-x) (z²+zx+x²) = 0

5.  (x+1) (x²-x+1) + (2x-1) (4x²+2x+1 )-(x-1) (x²+x+1)

Solution:

Given (x+1) (x²-x+1) + (2x-1) (4x²+2x+1 )-(x-1) (x²+x+1)

= (x)³ + (1 )³ + (2x)³ – (1 )³ (x)³ – (1 )³}

= x³ + 1 + 8x³ – 1- (x³ – 1)

= 9x³ – x³ + 1

= 8x³+ 1

(x+1) (x²-x+1) + (2x-1) (4x²+2x+1 )-(x-1) (x²+x+1) = 8x³+ 1

6. If x + \(\frac{1}{x}\)= -1 then find the value of (x³ – 1).

Solution:

Given x + \(\frac{1}{x}\)= -1

\(\left(x+\frac{1}{x}\right) x=-1(x)\)

x²+x+1=0[by transposition]

x³-1

or, (x-)x ×  x²+x+1

=(x-1)×0=0

The value of (x³ – 1)=0

7.  If a + \(\frac{9}{a}\)= 3 then find the value of (a3 + 27).

Solution:

Given a + \(\frac{9}{a}\)= 3

or, \(\frac{a^2+9}{a}\) = 3

or, a²+9=3a

or, a² – 3a + 9 = 0

= a³+ 27 = (a)³+ (3)³

= (a + 3) {(a)² – a.3 + (3)²}

= (a + 3) (a² – 3a + 9)

= (a + 3) x 0 = 0

The value of (a³ + 27) = 0

8. If \(\frac{a}{b}+\frac{b}{a}\)= 1 then find the value of (a3 + b3).

Solution:

Given \(\frac{a}{b}+\frac{b}{a}\)= 1

= \(\frac{a}{b}+\frac{b}{a}\)= 1

= \(\frac{a^2+b^2}{a b}=1\)

a² +b²=ab

or, a²-ab+b²= 0

∴ a³ + b³

= (a + b) (a² – ab + b²)

= (a + b) x 0 = 0

The value of (a³ + b³) = 0

9. Let’s factorize the following algebraic expressions :

1. 1000a³+ 27b6

Solution:

Given 1000a³+ 27b6

= (10a)³ + (3b2)³

= (10a + 3b²) {(10a)² – 10a.3b² + (3b2)²}

= (10a + 3b²) (100a² – 30ab² + 9b4)

1000a³+ 27b6 = (10a + 3b²) (100a² – 30ab² + 9b4)

2. 1-216z³.

Solution:

Given 1-216z³

=(1)3-(6z)³

= (1- 6z) {(1)² + 1.6z + (6z)²}

= (1-6z) (1 + 6z + 36z²)

1-216z³ = (1-6z) (1 + 6z + 36z²)

3. m⁴-m

Solution:

Given m⁴-m

= m (m³ – 1)

= m{(m)³-(1)³}

= m (m-1) (m² + m + 1)

m⁴-m = m (m-1) (m² + m + 1)

4. 192a³ + 3

Solution:

Given 192a³ + 3

= 3 (64a³ + 1)

= 3 {(4a)³ + (1)³}

= 3 (4a + 1) {(4a)² – 4a. 1 + (1)²}

= 3 (4a+ 1) (16a²-4a + 1)

192a³ + 3 = 3 (4a+ 1) (16a²-4a + 1)

“WBBSE Class 8 Maths Chapter 5, Cubes summary”

5. 16a4x3³ + 54ay³

Solution:

Given 16a4x3³ + 54ay³

= 2a (8a³x³ + 27y³)

= 2a {(2ax)³ + (3y)³}

= 2a (2ax + 3y) {(2ax)² – 2ax.3y + (3y)²}

= 2a (2ax + 3y) (4a²x² – 6axy + 9y²)

16a4x3³ + 54ay³ = 2a (2ax + 3y) (4a²x² – 6axy + 9y²)

6. 729a³b3c³ – 125

Solution:

Given 729a³b3c³ – 125

= (9abc)³ – (5)³

= (9abc – 5) {(9abc)² + 9abc.5 + (5)2}

= (9abc – 5) (81a²b2c² + 45abc + 25)

729a³b3c³ – 125 = (9abc – 5) (81a²b2c² + 45abc + 25)

7. \(\frac{27}{a^3}-\frac{1}{27 b^3}\)

Solution:

Given \(\frac{27}{a^3}-\frac{1}{27 b^3}\)

⇒ \(\left(\frac{3}{a}\right)^3-\left(\frac{1}{3 b}\right)^3 \)

⇒ \(\left(\frac{3}{a}-\frac{1}{3 b}\right)\left\{\left(\frac{3}{a}\right)^2+\frac{3}{a} \cdot \frac{1}{3 b}+\left(\frac{1}{3 b}\right)^2\right\} \)

⇒ \(\left(\frac{3}{a}-\frac{1}{3 b}\right)\left(\frac{9}{a^2}+\frac{1}{a b}+\frac{1}{9 b^2}\right)\)

\(\frac{27}{a^3}-\frac{1}{27 b^3}\)= \(\left(\frac{3}{a}-\frac{1}{3 b}\right)\left(\frac{9}{a^2}+\frac{1}{a b}+\frac{1}{9 b^2}\right)\)

8. \(\frac{x^3}{64}-\frac{64}{x^3}\)

Solution:

Given \(\frac{x^3}{64}-\frac{64}{x^3}\)

⇒ \(\left(\frac{x}{4}\right)^3-\left(\frac{4}{x}\right)^3\)

⇒ \( \left(\frac{x}{4}-\frac{4}{x}\right)\left\{\left(\frac{x}{4}\right)^2+\frac{x}{4} \cdot \frac{4}{x}+\left(\frac{4}{x}\right)^2\right\} \)

⇒\( \left(\frac{x}{4}-\frac{4}{x}\right)\left\{\left(\frac{x}{4}\right)^2+2 \cdot \frac{x}{4} \cdot \frac{4}{x}+\left(\frac{4}{x}\right)^2-\frac{x}{4} \cdot \frac{4}{x}\right\} \)

⇒ \(\left(\frac{x}{4}-\frac{4}{x}\right)\left\{\left(\frac{x}{4}+\frac{4}{x}\right)^2-1\right\} \)

⇒ \( \left(\frac{x}{4}-\frac{4}{x}\right)\left\{\left(\frac{x}{4}+\frac{4}{x}\right)^2-(1)^2\right\} \)

⇒ \(\left(\frac{x}{4}-\frac{4}{x}\right)\left(\frac{x}{4}+\frac{4}{x}+1\right)\left(\frac{x}{4}+\frac{4}{x}-1\right)\)

\(\frac{x^3}{64}-\frac{64}{x^3}\)=  \(\left(\frac{x}{4}-\frac{4}{x}\right)\left(\frac{x}{4}+\frac{4}{x}+1\right)\left(\frac{x}{4}+\frac{4}{x}-1\right)\)

9. x³ + 3x²y + 3xy² + 2y³

Solution:

Given x³ + 3x²y + 3xy² + 2y³

= x³ + 3x²y + 3xy² + y³ + y³

= (x + y)³ + y³

= (x + y + y) {(x + y)² – (x + y) y + (y)²}

= (x + 2y) (x² + 2xy + y²– xy – y² + y²)

= (x + 2y) (x² + xy + y²)

x³ + 3x²y + 3xy² + 2y³ = (x + 2y) (x² + xy + y²)

10. 1 + 9x + 27x² + 28x³

Solution:

Given 1 + 9x + 27x² + 28x³

= 1 + 9x + 27x² + 27x³ + x³ .

= (1)³ + 3.(1 )² .3x + 3.1. (3x)² + (3x)³ + x³

= (1 + 3x)³ + (x)³

= (1 + 3x + x) {(1 + 3x)² – (1 + 3x) x + (x)²}

= (1 + 4x) (1 + 6x + 9x² – x – 3x² + x²)

= (1 + 4x) (1 + 5x + 7x²)

1 + 9x + 27x² + 28x³  = (1 + 4x) (1 + 5x + 7x²)

11.  x³ – 9y³ – 3xy (x – y)

Solution:

Given x³ – 9y³ – 3xy (x – y)

= x³ – 9y³ – 3x²y + 3xy²

= x2 – 3x²y + 3xy² – y³ – 8y³

= (x – y)³– (2y)³

= (x – y – 2y) {(x-y)² + (x-y) 2y + (2y)²}

= (x-3y) (x² – 2xy + y² + 2xy – 2y² + 4y²)

= (x – 3y) (x² + 3y²)

x³ – 9y³ – 3xy (x – y) = (x – 3y) (x² + 3y²)

12. 8-a³ + 3a²b – 3ab² + b³

Solution:

Given 8-a³ + 3a²b – 3ab² + b³

= 8- (a³ – 3a²b + 3ab² – b³)

= (2)³ – (a – b)³

= {2 – (a -b)}{(2)² + 2(a – b) + (a-b)²}

= (2 – a + b) (4 + 2a – 2b + a² – 2ab + b²)

8-a³ + 3a²b – 3ab² + b³ = (2 – a + b) (4 + 2a – 2b + a² – 2ab + b²)

13. x⁶ + 3x⁴b² + 3x²b⁴ + b⁶ + a³b³

Solution:

Given x⁶ + 3x⁴b² + 3x²b⁴ + b⁶ + a³b³

= (x²)³+ 3.(x²)².b² + 3.x².(b²)² + (b²)³ + a³b³

= (x² + b²)³ + (ab)³

= (x² + b² + ab) {(x² + b²)² – (x² + b²) ab + (ab)²}

= (x² + b² + ab) (x⁴ + 2x²b² + b⁴ – x²ab – ab³ + a²b²)

= (x² + ab + b²) (x⁴ + 2x²b² – abx² + a²b² – ab³ + b⁴)

x⁶ + 3x⁴b² + 3x²b⁴ + b⁶ + a³b³ = (x² + ab + b²) (x⁴ + 2x²b² – abx² + a²b² – ab³ + b⁴)

14.  x⁶+27

Solution:

Given x⁶+27

= (x²)³ + (3)³

= (x² + 3) {(x²)² – x².3 + (3)²}

= (x² + 3) (x⁴ – 3x² +9)

x⁶+27 = (x² + 3) (x⁴ – 3x² +9)

15.  x⁶ – y⁶

Solution:

Given x⁶ – y⁶

= (x³)² – (y³)² = (x³ + y³) (x³ – y³)

= (x + y) (x² – xy + y²) (x – y) (x² + xy + y²)

= (x + y) (x – y) (x² – xy + y²) (x² + xy + y²)

x⁶ – y⁶ = (x + y) (x – y) (x² – xy + y²) (x² + xy + y²)

16.  x¹²– y

Solution:

Given x¹²– y

= (x⁶)² – (y⁶)²

= (x⁶ + y⁶) (x⁶ – y⁶)

= {(x²)³+(y²)³} {(x³)² – (y³)²}

= (x² + y²) {(x²)²– x².y² + (y²)²} (x³ + y³) (x³ – y³)

= (x²+ y²) (x⁴– x²y² + y⁴) (x + y).(x²– xy + y²) (x-y) (x² + xy + y²)

= (x + y) (x – y) (x² + y²) (x² – xy + y²) (x² + xy + y²) (x⁴ – x²y² + y⁴)

x¹²– y = (x + y) (x – y) (x² + y²) (x² – xy + y²) (x² + xy + y²) (x⁴ – x²y² + y⁴)

“WBBSE Class 8 Maths Chapter 5 Cubes, definitions and examples”

17. m³ – n³ – m (m² – n²) + n(m – n)

Solution:

Given m³ – n³ – m (m² – n²) + n(m – n)

= (m-n) (m²+mn+n²) -m(m+n) (m-n) +n(m-n)(m-n)

= (m-n) (ref + rpfi + rf – ryf – rprfi + mn -rf) –

= (m-n) mn = mn (m-n)

m³ – n³ – m (m² – n²) + n(m – n) = mn (m-n)

Rational Numbers

The bus left at 8 o’clock in the morning. We fifteen friends have taken seats in the bus. But after some time the bus becomes crowded. Tamal shall try to write the room of the equation on a card.

Question 1. Let’s assume x more passengers other than us have boarded the bus.

Solution:

Given

Let’s assume x more passengers other than us have boarded the bus.

If now there are 32 passengers, then we get, x + 15 = 32 ………..(1)

or, x = 32 – 15

∴  x=17

∴ 17 more passengers have boarded the bus.

Tamal wrote on a piece of paper: The root of equation no. (1) is a natural number.

If there were 15 more passengers,

i.e., X + 15 = 15 ………….(2) then we get X = 0

Read and Learn More WBBSE Solutions For Class 8 Maths

∴  In that case the root of equation (2) is Natural Number (Natural Number / Whole number)

But Ayesha wrote by mistake X + 35 = 32.

X + 35 = 32……….(3) Let’s see what root w*e get solving the equation

X + 35 = 32

x = -3 The root of the equation (3) is – 3.

Tamal wrote the root of the equation (3) is [integer] [Integer / whole number)

Nasir also writes by mistake 2x + 15 = 32

Question 2. Let’s solve the equation 3x + 40 = 32 and find out the root.

Solution:

Given

3x + 40 = 32

or, 3x = 32 – 40

or, 3x = -8

∴ x = \(\frac{-8}{3}\)

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

It is seen the root of this equation is  \(\frac{-8}{3}\)

\(\frac{-8}{3}\) is a Rational number.

“WBBSE Class 8 Maths Chapter 3 solutions, Rational Numbers”

Let’s solve the equations below :

(1) 5x = 30

Solution:

Given

5x = 30

or, x = \(\frac{30}{5}\)

or, x= 6

2. 2x + \(\frac{x-1}{2}\) = 5

Solution:

Given

2x + \(\frac{x-1}{2}\) = 5

or, \(\frac{4 x+x-1}{2}\) = 5

or, 5x-1 = 10

or, 5x = 10+1=11

or, x= \(\frac{11}{5}=2 \frac{1}{5}\)

3. \(\frac{x}{5}+\frac{2}{7}=\frac{x}{10}\)

Solution:

Given

\(\frac{x}{5}+\frac{2}{7}=\frac{x}{10}\)

= \(\frac{x}{5}-\frac{x}{10}=-\frac{2}{7}\)

= \(\frac{2 x-x}{10}=-\frac{2}{7}\)

= \(\frac{x}{10}=\frac{2}{7}\)

= \(x=-\frac{2}{7} \times 10\)

= \(x=-\frac{20}{7}=-2 \frac{6}{7}\)

4. \(\frac{x}{4}+\frac{1}{2}=\frac{1}{2}\)

Solution:

Given

\(\frac{x}{4}+\frac{1}{2}=\frac{1}{2}\)

or, \(\frac{x}{4}=\frac{1}{2}-\frac{1}{2}\)

or, \(\frac{x}{4}=0\)

or, x = 0

We see the root of each equation is a Rational Number.

Question 3. But let’s see which number I get if I subtract two rational numbers.

Solution:

It is seen by subtracting two rational numbers I got a Rational number.

⇒ \(\left(-\frac{2}{3}\right)-\left(\frac{3}{8}\right)=-\frac{2}{3}-\frac{3}{8}=\frac{-16-9}{24}=-\frac{25}{24}\)

Question 4. Let’s see which number I get by multiplying two rational numbers.

Solution:

⇒ \(\left(-\frac{2}{3}\right) \times\left(\frac{3}{8}\right)=-\frac{1}{4}\)

It is seen by multiplying two rational numbers I got a Rational number.

“Class 8 WBBSE Maths Chapter 3 solutions, Rational Numbers study material”

Question 5. Let’s see which number I get by dividing two rational numbers.

Solution:

⇒ \(\left(-\frac{2}{3}\right) \div\left(\frac{3}{8}\right)=-\frac{2}{3} \times \frac{8}{3}=-\frac{16}{9}\)

It is seen by dividing these two rational numbers I got a number I got a Rational number. But let’s see what I get from \(\left(-\frac{2}{3}\right) \div 0\)

If a and b are two rational numbers then (a+b) is a rational number, (a – b) or (b – a) are Rational numbers, (a x b)= Rational number. But a ÷ b is always a rational number if b ≠ 0.

Let’s see what I get by adding O with any rational numbers.

= \(0+\frac{3}{7}=\frac{3}{7}\) and \(\frac{3}{7}+0=\frac{3}{7}\).

Let’s see what I shall get by multiplying and rational number by 1,

= \(1 \times \frac{3}{7}=\frac{3}{7}\) and \(\frac{3}{7} \times 1=\frac{3}{7}\)

Sima got by adding with zero two rational numbers and multiplying two rational numbers by,

0+ any rational = + 0 = Thai rational number That rational number

1x any rational number = That rational number x 1 = That rational number i.e., 0 + a = a + 0 = a and 1 x a = a 1 = a [ There a is any rational number]

1multiply any rational numbers with 0 and see what I shall find.

“WBBSE Class 8 Maths Chapter 3, Rational Numbers solved examples”

= \(0 \times \frac{14}{19}=0, \quad \frac{14}{19} \times 0=0\)

∴ Dipu multiplied any two rational numbers with 0.

0 x any rational number = any rational number 0 = 0

[ Take any rational number and do myself ]

0 x a = a x 0 = 0 (Here a is any rational number).

Write understanding below the chart and see where commutative law observes.

Question 6. I take any three rational numbers and add:

Solution:

= \(-\frac{1}{5}+\left(\frac{2}{5}+\frac{5}{7}\right)=\frac{32}{35}\)

and \(\left(-\frac{1}{5}+\frac{2}{5}\right)+\frac{5}{7}=\frac{32}{35}\)

∴ \(-\frac{1}{5}+\left(\frac{2}{5}+\frac{5}{7}\right) \left(-\frac{1}{5}+\frac{2}{5}\right)+\frac{5}{7}\)

∴ \(-\frac{1}{5}, \frac{2}{5}\) and \(\frac{5}{7}\)

Question 7. Subtract with any three rational numbers and see what we get.

Solution:

⇒ \(\frac{3}{5}-\left(\frac{2}{7}-\frac{1}{4}\right)=\frac{79}{140}\)

⇒ \(\left(\frac{3}{5}-\frac{2}{7}\right)-\frac{1}{4}=\frac{9}{140}\)

∴ \(\frac{3}{5}-\left(\frac{2}{7}-\frac{1}{4}\right)\) ≠ \(\left(\frac{3}{5}-\frac{2}{7}\right)-\frac{1}{4}\)

∴The substance of the rational numbers does not obey associative law.

Generally a-(b-c) ≠ (a-b)-c [where a,b,c are three rational numbers]

Question 8. I multiply with any three rational numbers and see of the multiplication of the rational numbers obeys Associative law.

Solution:

⇒ \(\frac{5}{8} \times\left(\frac{3}{5} \times \frac{7}{9}\right)=\frac{7}{24}\) and \(\left(\frac{5}{8} \times \frac{3}{5}\right) \times \frac{7}{9}=\frac{7}{24}\)

⇒ \(\frac{5}{8} \times\left(\frac{3}{5} \times \frac{7}{9}\right)\) ≠ \(\) [=/≠write]

⇒ \(\frac{5}{8}, \frac{3}{5}, \frac{7}{9}\) obeys associative law.

Question 9. Taking any three rational numbers Shuvam examined where the multiplication of the rational numbers obeys associative law.

Solution:

We get, a×(b×c) = (a×b)×c [Where a,b,c are rational numbers ]

⇒  \(\frac{1}{2}, \frac{2}{3}\) and \(\frac{5}{6}\) are three rational numbers.

⇒ \(\frac{1}{2} \times\left(\frac{2}{3} \times \frac{5}{6}\right)=\frac{1}{2} \times \frac{5}{9}=\frac{5}{18}\)

Again, \(\left(\frac{1}{2} \times \frac{2}{3}\right) \times \frac{5}{6}=\frac{1}{3} \times \frac{5}{6}=\frac{5}{18}\)

We see that multiplication of three rational numbers obeys associative law.

“WBBSE Class 8 Rational Numbers solutions, Maths Chapter 3”

Question 10. I decide any three rational numbers and see whether the division of the rational numbers obeys the commutative law of addition.

Solution:

⇒ \(\frac{11}{13} \div\left(\frac{5}{6} \div \frac{3}{8}\right)=\frac{11}{13} \div\left(\frac{5}{6} \times \frac{8}{3}\right)=\frac{11}{13} \div \frac{20}{9}=\frac{11}{13} \times \frac{9}{20}=\frac{99}{260}\)

But \(\left(\frac{11}{13} \div \frac{5}{6}\right) \div \frac{3}{8}=\left(\frac{11}{13} \times \frac{6}{5}\right) \div \frac{3}{8}=\frac{66}{65} \times \frac{8}{3}=\frac{176}{65}\)

∴ \(\frac{11}{13} \div\left(\frac{5}{6} \div \frac{3}{8}\right) \neq\left(\frac{11}{13} \div \frac{5}{6}\right) \div \frac{3}{8}\)

Division of rational numbers does not obey associative law.

Let’s see which number will be added to the rational number to make it zero.

⇒ \(\frac{3}{7}+\frac{-3}{7}=0 \text { and } \frac{3}{7}=0 \frac{-3}{7}\)

Joseph drew another card \(-\frac{2}{9}\)

⇒ \(\frac{-2}{9}+\left\{-\left(\frac{-2}{9}\right)\right\}=0\)

Adding ⇒ \(\frac{-2}{9}\) with \(-\left(\frac{-2}{9}\right)\) we get 0

⇒ \(\frac{2}{9}+\left(\frac{-2}{9}\right)=0\)

Question 12. \(\frac{9}{13}\)

Solution:

Given

\(\frac{9}{13}\)

⇒ \(\frac{9}{13} \times \frac{13}{9}=1 \text { or } \frac{13}{9} \times \frac{9}{13}=1\)

i.e., if \(\frac{9}{13}\) is multiplied by the reciprocal of \(\frac{9}{13}\) or \(\frac{13}{9}\), we get 1

Appu drew 1 \(-\frac{11}{7}\) , \(\left(-\frac{11}{7}\right)\) lets write by which rational numbers

\(\left(-\frac{11}{7}\right) \times-\frac{7}{11}\) = 1 and \(-\frac{7}{11}\) × \(-\frac{11}{7}\)= 1

∴ \(a \times \frac{1}{a}\) = 1  \(\frac{1}{a} \times a\)[where a is a rational number and a≠0]

But Rana picked up → 5/7 , 7/8 , or 11/12

He wrote \(\frac{5}{2} \times\left(\frac{7}{8}+\frac{11}{12}\right)=\frac{5}{2} \times\left(\frac{21+22}{24}\right)\)

⇒ \(\frac{5}{2} \times \frac{43}{24}=\frac{215}{48}\)

But \(\frac{5}{2} \times \frac{7}{8}+\frac{5}{2} \times \frac{11}{12}=\frac{35}{16}+\frac{55}{24}=\frac{215}{48}\)

It is seen \(\frac{5}{2} \times\left(\frac{7}{8}+\frac{11}{12}\right)\) = \(\frac{5}{2} \times \frac{7}{8}+\frac{5}{2} \times \frac{11}{12}\) [write =/≠]

Rational Numbers Exercise

1. Adding \(\frac{2}{9}\) with \(-\frac{2}{9}\) we shall get

2. Adding \(-\frac{9}{8}\) with \(\frac{9}{8}\) we shall get

3. Adding \(-\left(-\frac{5}{2}\right)\) with \(-\frac{5}{2}\) we shall get zero

4. Adding \(\frac{5}{8}\) with \(\frac{8}{5}\) we shall get

5. Adding \(-\frac{3}{9}\) with \(-\frac{9}{3}\) we shall get

6. Let’s multiply \(\frac{7}{9} \times\left(-\frac{11}{25}\right) \times\left(-\frac{89}{41}\right) \times\left(\frac{5}{121}\right)\) using commutative law and associative law.

Solution:

Given

\(\frac{7}{9} \times\left(-\frac{11}{25}\right) \times\left(-\frac{89}{41}\right) \times\left(\frac{5}{121}\right)\)

Using commutative law,

⇒ \(\left(-\frac{89}{41}\right) \times\left(\frac{5}{121}\right) \times \frac{7}{9} \times\left(-\frac{11}{25}\right)\)

⇒ \(\frac{-89}{41} \times \frac{5}{121} \times \frac{7}{9} \times \frac{-11}{25}\)

⇒ \(\frac{89}{41} \times \frac{5}{121} \times \frac{7}{9} \times \frac{11}{25}\)

⇒ \(\frac{623}{20295}\)

Using associative law,

⇒ \(\frac{7}{9}\left\{\left(\frac{-11}{25}\right) \times\left(\frac{-89}{41}\right) \times\left(\frac{5}{121}\right)\right\}\)

⇒ \(\frac{7}{9}\left(\frac{11}{25} \times \frac{89}{41} \times \frac{5}{121}\right)\)

⇒ \(\frac{7}{9} \times \frac{89}{2255}=\frac{623}{20295}\)

Now by dividing the distance between 0 to 1 into 5 equal parts, let put \(\frac{1}{5}\) and \(\frac{2}{5}\) at the right extremities of the first part and the second part respectively.

Dividing the distance between 0 to 1 into 5 equal parts, if I make same distance, I shall get → \(0, \frac{1}{5}, \frac{2}{5} \frac{3}{5}, \frac{4}{5} \frac{5}{5}=1\)

Again dividing the distance between 1 to 2 into 5 equal parts, I shall get → \(\frac{6}{5}, \frac{7}{5}, \frac{8}{5}, \frac{9}{5}, \frac{10}{5}=2\)

Dividing the distance between 1 into 5 equal parts, we get \(0,-\frac{1}{5},-\frac{2}{5},-\frac{3}{5},-\frac{4}{5},-\frac{5}{5}=-1\)

∴ Again dividing the distance between -2 to -1 into 5 equal parts, we get \(\frac{6}{5},-\frac{7}{5},-\frac{8}{5},-\frac{9}{5}, \frac{10}{5}=-2\)

Between and \(\frac{2}{5}\) and \(\frac{4}{5}\) let’s examine is there a rational number?

\(\frac{3}{5} \frac{2}{5}=\frac{4}{10}\) and \(\frac{4}{5}=\frac{8}{10}\)

It is seen that in between \(\frac{4}{10}\) and \(\frac{8}{10}\) we can write the rational number \(\frac{5}{10}, \frac{6}{10}, \frac{7}{10}\)

Again, \(\frac{2}{5}=\frac{4}{10}=\frac{40}{100}\) and \(\frac{4}{5}=\frac{8}{10}=\frac{80}{100}\)

∴ In between \(\frac{40}{100}\) and \(\frac{80}{100}\) we can write the rational number \(\frac{41}{100}, \frac{42}{100}, \ldots \ldots, \frac{79}{100}\)

∴ There are infinite rational numbers in between \(\frac{2}{5}\) and \(\frac{4}{5}\).

We get infinite (finite/infinite/rational numbers in between any two rational numbers.)

Rational Numbers Exercise

Question 1. Let’s solve the following equations and express the root in the form (where q≠0 and p,q are two integers)

1. 7x=14

Solution:

Given

7x=14

⇒ \(7 x=\frac{14}{7}\)

⇒ \(x=\frac{2}{1}\)

(Here p=2,q=1)

x=2

2. 4p+32=0

Solution:

Given

4p+32=0

⇒ 4p=-32

p=\(\frac{-32}{4}\)

p=\(\frac{-8}{1}\)

(Here p=-8,q=1)

p=-8

3. 11x=0

Solution:

Given

11x=0

x= \(\frac{0}{11}\)

(Here p=0,q=11)

x=0

4. 5m-3=0

Solution:

Given

5m-3=0

⇒ 5m=3

⇒ m= \(\frac{3}{5}\)

(Here p=3,q=5)

m= \(\frac{3}{5}\)

5. 9y+18=0

Solution:

Given

9y+18=0

⇒ 9y=-18

y= \(\frac{-18}{9}\)

y= \(\frac{-2}{1}\)

(Here p=-2,q=1)

y=-2

6. t=8-12t

Solution:

Given

t=8-12t

⇒ t+12t=8

⇒ 13t=8

⇒ t= \(\frac{8}{13}\)

(Here p=8,q=13)

t= \(\frac{8}{13}\)

7. 6y=5+y

Solution:

Given

6y=5+y

⇒ 6y-y=5

⇒ 5y=5

⇒ y= \(\frac{5}{5}\)

⇒ y= \(\frac{1}{1}\)

(Here p=1,q=1)

y=1

8. 2x+4=12

Solution:

Given

2x+4=12

2x+4=12

⇒ 2x=12-4

⇒ 2x=8

⇒ x= \(\frac{8}{2}\)

⇒ x= \(\frac{4}{1}\)

(Here p=4,q=1)

x=4

“WBBSE Class 8 Chapter 3 Maths, Rational Numbers step-by-step solutions”

Question 2. let’s verify if y=\(\frac{-5}{4}\) then \(\frac{-5}{4}\) = y.

Solution:

y= \(y=\frac{-5}{4}\)

L.H.S. = -(-y)

= \(-\left\{-\left(\frac{-5}{4}\right)\right\}\) = \(-\left\{\frac{5}{4}\right\}=-\frac{5}{4}\) = Y = R.H.S.(proved).

1. 2x+5

Solution:

Given 2x + 5

= \(2\left(-\frac{3}{8}\right)+5\)

= \(-\frac{3}{4}+\frac{5}{1}\)

= \(\frac{-3+20}{4}=\frac{17}{4}\)

2x + 5 = \(\frac{-3+20}{4}=\frac{17}{4}\)

2. x+ \(x+\frac{3}{8}\)

Solution:

Given x+ \(x+\frac{3}{8}\)

⇒ \( x+\frac{3}{8}\)

= \(-\frac{3}{8}+\frac{3}{8}\)

= 0

x+ \(x+\frac{3}{8}\) = 0

“Class 8 Maths Rational Numbers solutions, WBBSE syllabus”

3. 5-(-x)

Solution:

Given 5 – (-x)

⇒ \(5-\left\{-\left(-\frac{3}{8}\right)\right\}\)

⇒ \(5-\left\{\frac{3}{8}\right\}\)

⇒ \(5-\frac{3}{8}\)

⇒ \(\frac{40-3}{8}\)

⇒ \(\frac{37}{8}\)

⇒ \(4 \frac{5}{8}\)

5 – (-x) = \(4 \frac{5}{8}\)

4. 6-(-x)

Solution:

Given 6 – (-x)

= \(6-\left\{-\left(-\frac{3}{8}\right)\right\}\)

= \(6-\left\{\frac{3}{8}\right\}\)

= \(6-\frac{3}{8}\)

= \(\frac{48-3}{8}\)

= \(\frac{45}{8}\)

= \(5 \frac{5}{8}\)

6 – (-x) = \(5 \frac{5}{8}\)

“WBBSE Class 8 Maths Chapter 3, Rational Numbers important questions”

Question 4. Let’s write the appropriate number in the following boxes:

Solution:

1. \(\frac{9}{11}+-\frac{9}{11}=0 \)

2. \( \frac{21}{29}+\left(-\frac{21}{29}\right)=0\)

3. \(\frac{7}{19} \times \frac{19}{7}=1\),

4. \(-5 \times-\frac{1}{5}=1\)

5. \(\frac{-15}{23} \times-\frac{23}{15}=1\)

6. (\(\left(-\frac{8}{3}\right) \times\left(-\frac{21}{20}\right)=\frac{14}{15}\)

Question 5. Multiplying \(\frac{7}{18}\) with the reciprocal of \(\left(-\frac{5}{6}\right)\), lets write the product.

Solution:

Reciprocal of \(-\frac{5}{6}\) is = \(-\frac{6}{5}\)

∴ \(\frac{7}{18} \times\left(-\frac{6}{5}\right)\)

= \(-\frac{7}{18} \times \frac{6}{5}\)

= \(-\frac{7}{15}\)

Question 6. Find the value of the following with the help of commutative law and associative law.

Solution:

1. \(\frac{5}{8}+\left(-\frac{7}{15}\right)+\left(\frac{3}{32}\right)+\left(\frac{11}{75}\right)\)

Solution:

Given \(\frac{5}{8}+\left(-\frac{7}{15}\right)+\left(\frac{3}{32}\right)+\left(\frac{11}{75}\right)\)

⇒ \(\left(\frac{5}{8}+\frac{3}{32}\right)+\left(\frac{11}{75}-\frac{7}{15}\right)\)

⇒ \(\left(\frac{20+3}{32}\right)+\left(\frac{11-35}{75}\right)\)

⇒ \(\frac{23}{32}+\left(-\frac{24}{75}\right)\)

⇒ \(\frac{23}{32}-\frac{8}{25}\)

⇒ \( \frac{575-256}{800}\)

⇒ \(\frac{319}{800}\)

2. \(\frac{8}{121} \times \frac{35}{169} \times \frac{55}{36} \times \frac{78}{49}\)

Solution:

Given \(\frac{8}{121} \times \frac{35}{169} \times \frac{55}{36} \times \frac{78}{49}\)

⇒ \(\left(-\frac{8}{121} \times \frac{55}{36}\right)\) × \(\left(\frac{35}{169} \times \frac{78}{49}\right)\)

⇒ \(\frac{10}{99} \times \frac{30}{93}\)

⇒ \(\frac{100}{3003}\)

Question 7. Let’s put the rational numbers in the number line: \(\frac{1}{4},-\frac{3}{4},-\frac{2}{3}, \frac{6}{5},-\frac{8}{3}\) 

Solution:

Question 8. 4 rational numbers which age greater than rational numbers.

Solution:

⇒ \(\frac{1}{2}, 1 \frac{1}{3}, 1 \frac{1}{4}, 1 \frac{1}{5}\)

Question 9. Let’s find 4 rational numbers between and \(\frac{3}{5}\) \(4 \frac{1}{2}\). \(-\frac{3}{5}=-\frac{6}{10}, \frac{1}{2}=\frac{5}{10}\)

Solution:

⇒ \(-\frac{3}{5}=-\frac{6}{10}, \frac{1}{2}=\frac{5}{10}\)

Between \(\frac{-6}{10}\) and \(\frac{5}{10}\) rational numbers are

⇒ \(\frac{-5}{10},-\frac{4}{10},-\frac{3}{10},-\frac{2}{10},-\frac{1}{10}, 0, \frac{1}{10}, \frac{2} {10}, \frac{3}{10}, \frac{4}{10}\)

Or, \(-\frac{1}{2},-\frac{2}{5}\) \(-\frac{3}{10}, \frac{1}{5},-\frac{1}{10}, 0, \frac{1}{10}, \frac{1}{5}, \frac{3}{10}, \frac{2}{5}\)

“Class 8 WBBSE Maths Chapter 3, Rational Numbers easy explanation”

Question 10. We write five rational numbers between the two rational numbers given below.

Solution:

1. \(\frac{1}{3}\) and \(\frac{3}{5}\)

Solution:

Given \(\frac{1}{3}\) and \(\frac{3}{5}\)

\(\frac{1}{3}=\frac{5}{15}=\frac{10}{30}, \frac{3}{5}=\frac{9}{15}=\frac{18}{30}\)]

= 10

2. Between \(\frac{1}{3}\) and \(\frac{3}{5}\) we five rational numbers:

Solution:

Given \(\frac{1}{3}\) and \(\frac{3}{5}\)

⇒ \(\frac{11}{30}, \frac{12}{30}, \frac{13}{30}, \frac{14}{30}, \frac{15}{30} \text { or, } \frac{11}{30}, \frac{2}{5}, \frac{13}{30}, \frac{7}{15}, \frac{1}{2}\)

3. \(\frac{1}{4}\) and \(\frac{1}{2}\)

Solution:

Given \(\frac{1}{4}\) and \(\frac{1}{2}\)

⇒ \(\frac{1}{4}=\frac{6}{24}\) and \(\frac{1}{2}=\frac{12}{24}\)

Between \(\frac{1}{4}\) and \(\frac{1}{2}\) we five rational numbers are

⇒ \(\frac{7}{24}, \frac{8}{24}, \frac{9}{24}, \frac{10}{24}, \frac{11}{24} \text { or } \frac{7}{24}, \frac{1}{3}, \frac{3}{8}, \frac{5}{12}, \frac{11}{24}\) and \(\)

“WBBSE Class 8 Maths Chapter 3 solutions, Rational Numbers PDF”

4. \(\frac{4}{3}\) and \(\frac{3}{7}\)

Solution:

Given \(\frac{4}{3}\) and \(\frac{3}{7}\)

⇒ \(\frac{4}{3}=\frac{4 \times 7}{3 \times 7}=\frac{28}{21}\)

⇒ \(\frac{3}{7}=\frac{3 \times 3}{7 \times 3}=\frac{9}{21}\)

Between \(\frac{3}{7}\) and \(\frac{4}{3}\) we five rational numbers are

⇒ \(\frac{10}{21}, \frac{11}{21}, \frac{12}{21}, \frac{13}{21}, \frac{14}{21}\)

⇒ \(\frac{10}{21}, \frac{11}{21}, \frac{4}{7}, \frac{13}{21}, \frac{14}{21}\)

Multipilcation And Division Of Polynomials

Today we have decided to make some funny things and hang them in our classroom with the half of colourful charts. So we have made paper cuttings of various colours and sizes. My friends have written various numbers and expressions on some coloured papers and stuck them on the charts.

Let’s draw the pictures in the given blank spaces from the pictutres above.

Let’s draw cards showing constants.

Let’s draw cards showing monomial algebraic expressions.

Let’s find out the sum the monomials and write it in the blank space.

-6y+4y+3x²+7x²=-2y+10x²

Read and Learn More WBBSE Solutions For Class 8 Maths

Let’s write the binomial algebraic expressions and draw those cards in the blank space.

Let’s write the binomial algebraic expressions and draw those cards in the blank space.

5x+2y+(-7y-3x)

= 5x+2y-7y-3x

= 2x-5y

5x+2y+(-7y-3x) = 2x-5y

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

“WBBSE Class 8 Maths Chapter 4 solutions, Multiplication and Division of Polynomials”

(a + b – c) of 3. It is a trinomial expression, but (2x⁴+5y³-10y²-8) is an algebraic expression having 4 terms. It is a tetranomial expression.

What do we say if there are many terms in such an algebraic expression?

The algebraic expression having one or more terms is called a Polynomial expression.

Put Rupa made different types of funny things. She separated all the rectangular cards. She attached these to a big cardboard. Sakil wrote the area, length or breadth of these rectangular coloured cards. See the pictures and try to write the length, breadth or area of these rectangular cards of different colours.

1.4 Area of the yellow coloured rectangular card

= (7x – 18 – 3x² + x3) x (5 – x²) Sq. m.

= x³ – 3x² + 7x – 18 x – x² + 5 Sq. m.

= {(x³ – 3x² + 7x – 18) x (-x²) + (x3- 3x² + 7x – 18) x 5} Sq. m.

⇒ -x⁵ + 3x⁴ – 7x³ + 18x² + 5x³ – 15×2 + 35x – 90 Sq. m.

⇒ -x⁵ + 3x⁴ – 2x³ + 3x² + 35x – 90 Sq. m.

Multiplication And Division Of Polynomials Exercise

Question 1. Let’s find the product by successive multiplication

1. (x⁵+ 1) X (3 -x⁴), (4 + x³ +x⁶)

Solution:

Given

(x⁵ + 1), (3-x⁴), (4 + x³+x⁶)

= {x⁵(3-x⁴)+1(3-x⁴)}(4+x³+x⁶)

=(3x⁵ – x⁹ + 3 – x⁴) (4 + x³ + x⁶) .

= 3x⁵(4 + x³ +x⁶) – x⁹(4 + x³,+ x⁶) +3(4 + x³ + x⁶) – x⁴(4 + x³ + x⁶)

= 12x⁵ + 3x⁸ + 3x¹¹ -4x⁹-x¹²-x15 + 12 + 3x³ + 3x⁶ – 4x⁴ – x⁷– x¹⁰

= -x¹⁵– x¹²+ 3x¹¹– x¹⁰ – 4x⁹+ 3x⁸– x⁷ + 3x⁶ + 12×5- 4x⁴ + 3x³ + 12

(x⁵ + 1), (3-x⁴), (4 + x³+x⁶) = -x¹⁵– x¹²+ 3x¹¹– x¹⁰ – 4x⁹+ 3x⁸– x⁷ + 3x⁶ + 12×5- 4x⁴ + 3x³ + 12

“Class 8 WBBSE Maths Chapter 4 solutions, Polynomials study material”

2. (2a³ – 3b⁵), (2a³ + 3b⁵), (2a⁴ – 3a²b² + b⁴)

Solution:

Given

(2a³ – 3b⁵) x (2a³ + 3b⁵) (2a⁴ – 3a²b² + b⁴)

= {2a³(2a³ + 3b⁵) – 3b⁵ (2a³ + 3b⁵)} (2a⁴ – 3a²b² + b⁴)

= (4a⁶ + 6a³b⁵ – 6a³b⁵ – 9b¹⁰) (2a⁴ – 3a²b² + b⁴)

= (4a⁶ – 9b¹⁰) (2a⁴ – 3a²b² + b⁴)

= 4a⁶ (2a⁴ – 3a²b² + b⁴) – 9b¹⁰ (2a⁴ – 3a²b² + b⁴)

= 8a¹⁰ – 12a⁸ b² + 4a⁶b⁴ – 18 a⁴b¹⁰ + 27a²b12 – 9b¹⁴

(2a³ – 3b⁵) x (2a³ + 3b⁵) (2a⁴ – 3a²b² + b⁴) = 8a¹⁰ – 12a⁸ b² + 4a⁶b⁴ – 18 a⁴b¹⁰ + 27a²b12 – 9b¹⁴

3. (ax + by), (ax – by), (a⁴x⁴ + a²b²x²y² + b⁴y⁴)

Solution:

Given

(ax + by), (ax – by), (a⁴x⁴ + a²b²x²y² + b⁴y⁴)

= (ax + by) x (ax – by) (a⁴x⁴ + a²b²x²y² + b⁴y⁴)

= {ax (ax – by) + by (ax – by) (a⁴x⁴ + a²b²x²y² + b⁴y⁴)

= (a²x² – abxy + abxy – b²y²) (a⁴x⁴ + a²b²x²y² + b⁴y⁴)

= (a²x² – b²y²) (a⁴x⁴ + a²b²x²y²+ b⁴y⁴)

= a²x² (a⁴x⁴ + a²b²x²y² + b⁴y⁴) – b²y² (a⁴x⁴ + a²b²x²y² + b⁴y⁴)

= a⁶x⁶ + a⁴b²x⁴y² + a²b⁴x²y⁴ – a⁴b²x⁴y² – a²b⁴x²y⁴– b⁶y⁶

= a⁶x⁶ – b⁶y⁶

(ax + by), (ax – by), (a⁴x⁴ + a²b²x²y² + b⁴y⁴)= a⁶x⁶ – b⁶y⁶

4. (a + b + c), (a – b + c), (a + b – c)

Solution:

Given

(a + b + c), (a – b + c), (a + b – c)

(a + b + c) x (a – b + c), (a + b – c)

= {a (a – b + c) + b (a – b + c) + c (a – b + c)} (a + b – c)

= (a²– ab + ac + ab – b² + bc + ac – ba + c²) (a + b – c)

= (a² + 2ac – b² + c²) (a + b – c)

= a (a² + 2ac – b² + c²) + b (a² + 2ac – b²+c²) – c (a² + 2ac – b² + c²)

= a³ + 2a²c -ab²+ ac² + a²b + 2abc – b³ + bc² – a²c – 2ac²+ b²c – c3

= a³+ a²c – ab²– ac² + a²b + 2abc + be² + b²c – b³ – c³

= a³ – b³ – c³+ 2abc-+ a²b + a²c – ab² – ac² + b²c + bc²

(a + b + c), (a – b + c), (a + b – c)= a³ – b³ – c³+ 2abc-+ a²b + a²c – ab² – ac² + b²c + bc²

“WBBSE Class 8 Maths Chapter 4, Multiplication and Division of Polynomials solved examples”

5. \(\left(\frac{2 p^2}{q^2}+\frac{5 q^2}{p^2}\right)\left(\frac{2 p^2}{q^2}-\frac{5 q^2}{p^2}\right)\)

Solution:

Given

⇒ \(\left(\frac{2 p^2}{q^2}+\frac{5 q^2}{p^2}\right) \times\left(\frac{2 p^2}{q^2}-\frac{5 q^2}{p^2}\right)\)

⇒ \(\frac{2 p^2}{q^2}\left(\frac{2 p^2}{q^2}-\frac{5 q^2}{p^2}\right)+\frac{5 q^2}{p^2}\left(\frac{2 p^2}{q^2}-\frac{5 q^2}{p^2}\right)\)

⇒ \(\frac{4 p^4}{q^4}-\frac{10 p^2 q^2}{p^2 q^2}+\frac{10 p^2 q^2}{p^2 q^2}-\frac{25 q^4}{p^4}\)

⇒ \(\frac{4 p^4}{q^4}-\frac{25 q^4}{p^4}\)

6. \(\left(\frac{x^2}{y^2}+\frac{y^2}{z^2}\right),\left(\frac{y^2}{z^2}+\frac{z^2}{x^2}\right),\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)\)

Solution.

⇒ \(\left(\frac{x^2}{y^2}+\frac{y^2}{z^2}\right) \times\left(\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)\)

⇒ \(\left\{\frac{x^2}{y^2}\left(\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)+\frac{y^2}{z^2}\left(\frac{y^2}{z^2}+\frac{z^2}{x^2}\right)\right\}\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)\)

⇒ \(\left(\frac{x^2 y^2}{y^2 z^2}+\frac{x^2 z^2}{x^2 y^2}+\frac{y^4}{z^4}+\frac{y^2 z^2}{x^2 z^2}\right)\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)\)

⇒ \(\left(\frac{x^2}{z^2}+\frac{z^2}{y^2}+\frac{y^4}{z^4}+\frac{y^2}{x^2}\right) \cdot\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)\)

⇒ \(\frac{x^2}{z^2}\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)+\frac{z^2}{y^2}\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)+\frac{y^4}{z^4}\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)+\frac{y^2}{x^2}\left(\frac{z^2}{x^2}+\frac{x^2}{y^2}\right)\)

“WBBSE Class 8 Polynomials solutions, Maths Chapter 4”

⇒ \(\frac{x^2 z^2}{x^2 z^2}+\frac{x^4}{y^2 z^2}+\frac{z^4}{x^2 y^2}+\frac{x^2 z^2}{y^4}+\frac{y^4 z^2}{x^2 z^4}+\frac{x^2 y^4}{y^2 z^4}+\frac{y^2 z^2}{x^4}+\frac{x^2 y^2}{x^2 y^2}\)

⇒ \(1+\frac{x^4}{x^2 z^2}+\frac{z^4}{x^2 y^2}+\frac{x^2 z^2}{y^4}+\frac{y^4}{x^2 z^2}+\frac{x^2 y^2}{z^4}+\frac{y^2 z^2}{x^4}+1\)

⇒ \(2+\frac{x^4}{y^2 z^2}+\frac{y^4}{x^2 z^2}+\frac{z^4}{x^2 y^2}+\frac{y^2 z^2}{x^4}+\frac{x^2 z^2}{y^4}+\frac{x^2 y^2}{z^4}\)

Question 2. Simplify :

1. (x + y) (x² – xy + y²) + (x – y) (x² + xy + y²)

Solution:

Given

(x + y) (x² – xy + y²) + (x – y) (x² + xy + y²)

= x (x² – xy + y²) + y (x² – xy + y²) + x (x² + xy + y²) – y (x² + xy + y²)

= x³ – x²y + xy² + x²y – xy² + y³ + x³ + x2y + xy² – x²y – xy² – y³

= x³ + y³ + x³ – y³

= 2x³

(x + y) (x² – xy + y²) + (x – y) (x² + xy + y²)= 2x³

2. a² (b² – c²) + b² (c² – a²) + c² (a² – b²)

Solution:

Given

a² (b² – c²) + b² (c² – a²) + c² (a² – b²)

= a²b² – a²c² + b²c² – a²b² + a²c² – b²c²

= 0

a² (b² – c²) + b² (c² – a²) + c² (a² – b²) = 0

Question 3. 

1. If a = x² + xy + y², b= y²+ yz + z², c = z² + xz + x² then find the value of (x – y)a + (y – z)b + (z – x) c.

Solution:

Given

a = x² + xy + y², b= y²+ yz + z², c = z² + xz + x²

= (x – y)a + (y – z)b + (z – x) c

= (x – y) (x² + xy + y²) + (y – z) (y² + yz + z²) + (z – x) (z² + xz + x²)

= x³ – y³ + y³ – z³ + z³ – x³

= 0 . . .

The value of (x – y)a + (y – z)b + (z – x) c = 0 . . .

“Class 8 WBBSE Maths Chapter 4, Multiplication and Division of Polynomials easy explanation”

2. If a = lx + my + n, b = mx + ny + I, c = nx + ly + m, then find the value of a (m + n) + b(n +1) + c (I + m).

Solution:

Given

a = lx + my + n, b = mx + ny + I, c = nx + ly + m,

= a (m + n) + b(n + I) + c (I + m)

= (lx + my + n) (m + n) + (mn + ny +1) (n + I) + (nx + ly + m) (I + m)

= Imx + Inx + m²y + mny + mn + n² + mnx + Imx + n²y + Iny + In + I² + Inx + mnx + l²y + Imy + Im + m²

= l²+ m² + n² + 2lmx + 2lnx + 2mnx + l²y + m²y + n²y + Imy + Iny + mny + Im + In + mn

Mrinal and Sraboni have made very colourful cards. There are many algebraic expressions on these cards.

Multiplying the algebraic expressions of their cards, I have written the product on another card. My friend Niladri is trying to find the multiplicant or multiplier from the product written on cards.

Product of two numbers -s- One of them = The other one

The value of a (m + n) + b(n +1) + c (I + m) = l²+ m² + n² + 2lmx + 2lnx + 2mnx + l²y + m²y + n²y + Imy + Iny + mny + Im + In + mn

Question 4. Let’s multiply and then verify the quotient dividing the product by the multiplier or the muliplicant.

Solution:

(1 + 5x) x (4 – 3x) = (4 + 17x – 15x²)

= (4 + 17x – 15x²) ÷ (1 + 5x) = 4-3x

1. (a²-3a -2) x (2a- 1) = 2a³-7a²-a+2

Solution:

Given

(a²-3a -2) x (2a- 1) = 2a³-7a²-a+2

(2a³-7a²-a+2) ÷ ?(a²-3a+2) = 2a-1

2a-1

Quotient = 2a-1 and Remainder = 0

2. 27p³+9p²+3p+1×3p-1=81p⁴-1

Solution:

Given

27p³+9p²+3p+1×3p-1=81p⁴-1

Quotient =27p³+9p²+3p+1 and Remainder = 0

“WBBSE Class 8 Maths Chapter 4 solutions, Polynomials PDF”

Multiplication And Division Of Polynomials Exercise

Question 1. Let’s divide by arranging in decreasing powers of variables.

1. (x²– 13x + 22) by (x – 11)

Solution: 

Given

(x²– 13x + 22) and (x – 11)

Divided by arranging in decreasing powers of variables (x²– 13x + 22) by (x – 11) we get

Quotient = (x-2) and Remainder = 0

2. (a²-5a+6) by (a-2)

Solution: 

Given

(a²-5a+6) and (a-2)

Divided by arranging in decreasing powers of variables (a²-5a+6) by (a-2) we get

Quotient = (a-3) and Remainder = 0

3. (2a³-7a²-a+2) by (a²-3a-2)

Solution:

Given

(2a³-7a²-a+2) and (a²-3a-2)

Quotient = (2a-1) and Remainder = 0

4. (4a²-9b²) by (2a+3b)

Solution:

Given

(4a²-9b²) and (2a+3b)

Quotient = (2a-3b) and Remainder = 0

Question 2. Let’s find divisor and remainder of the expression in the red card.

Solution:

Divisor =6x³y- x²y² – 7xy³ + 12y⁴

Quotient = 2x + 3y

Dividend = (3x2y – 2x- 4)and Remainder= 3x-4

“WBBSE Class 8 Maths Chapter 4, Multiplication and Division of Polynomials important questions”

Question 3. Let’s find divisor and remainder of the expression in the blue card.

Solution:

The dividend = 12x⁴+5x³-33x²-3x+16 and divisor = 4x²-x-5

Dividend = 3x²+2x-4 and remainder = 3x-4

Question 4. Let’s find divisor and remainder of the expression in the green cards.

Solution:

Dividend = x and Remainders = = x

Multiplication And Division Of Polynomials Exercise 4.2

Question 1. The product of 2 numbers is 3x² + 8x + 4 and one number is 3x +2. Let’s find the other number.

Solution:

Given

The product of 2 numbers is 3x² + 8x + 4 and one number is 3x +2.

∴ Other number = (3x² + 8x + 4) – (3x + 2)

∴ Other number = (x+2)

Question 2. The area of a rectangle is (24x² – 65xy + 21 y²) sq. cm and length is (8x – 3y). Let’s find the breadth of it.

Solution:

Given

The area of a rectangle is (24x² – 65xy + 21 y²) sq. cm and length is (8x – 3y).

The area of a rectangle is (24x² – 65xy + 21 y²) sq. cm.

Length (8x – 3y) cm.

Breadth = (24x² – 65xy + 21 y²) -(8x – 3y)

∴ Breadth of the rectangle = (3x-7y)cm.

Question 3. If in a division problem, the dividend is x⁴+x³y+xy³-y⁴ and division is x²+xy-y². Then find the quotient and remainder.

Solution:

Given

If in a division problem, the dividend is x⁴+x³y+xy³-y⁴ and division is x²+xy-y².

Dividend x⁴+x³y+xy³-y⁴

Divisor x²+xy-y²

∴ Quotient = x²+y² and Remainder = 0

Question 4. Divide

1. (m² + 4m – 21) by (m – 3)

Solution:

Given

(m² + 4m – 21) and (m – 3)

Quotient = (m-7) and Remainder = 0

2. (6c²-7c+2) by Bold (3c-2)

Solution:

Given

(6c²-7c+2) and Bold (3c-2)

Quotient = (2c-2) and Remainder = 0

3. (2a⁴-a³-2a²+5a-1) by (2a²+a-3)

Solution:

Given

(2a⁴-a³-2a²+5a-1) and (2a²+a-3)

Quotient = (a²-a+1) and Remainder = (a+2)

4. (m⁴ – 2m³ – 7m² + 8m + 12) by (m² – m – 6)

Solution:

Given

(m⁴ – 2m³ – 7m² + 8m + 12) and (m² – m – 6)

Quotient = m²-m-2 and Remainder = 0

“WBBSE Class 8 Maths Chapter 4, Polynomials summary”

Question 5. 1 (6x²a³ – 4x³a² + 8x⁴a²) ÷ 2a²x²

Solution:

Given

(6x²a³ – 4x³a² + 8x⁴a²) and 2a²x²

⇒ \(\frac{6 x^2 a^3-4 x^3 a^2+8 x^4 a^2}{2 a^2 x^2}\)

⇒ \(\frac{6 x^2 a^3}{2 a^2 a^2}-\frac{4 x^3 a^2}{2 a^2 x^2}+\frac{8 x^4 a^2}{2 a^2 x^2}\)

= 3a-2x+4x²

2. \(\frac{2 y^9 x^5}{5 x^2} \times \frac{125 x y^5}{16 x^4 y^{10}}\)

Solution.

Given \(\frac{2 y^9 x^5}{5 x^2} \times \frac{125 x y^5}{16 x^4 y^{10}}\)

⇒ \(\frac{7 a^4 y^2}{9 a^2} \times \frac{729 a^6}{42 y^6}\)

⇒ \(\frac{27 a^{10} y^2}{2 a^2 y^6}=\frac{27 a^8}{2 y^4}\)

3. (p²q²r5 – p3q5r² + p5q3r²) – p²q²r²

“Class 8 Maths Polynomials solutions, WBBSE syllabus”

⇒ \(\frac{p^2 q^2 r^5-p^3 q^5 r^2+p^5 q^3 r^2}{p^2 q^2 r^2}\)

⇒ \(\frac{p^2 q^2 r^5}{p^2 q^2 r^2}-\frac{p^3 q^5 r^2}{p^2 q^2 r^2}+\frac{p^5 q^3 r^2}{p^2 q^2 r^2}\)

= r³-pq³+p³q

Question 6. In a division problem the Divisor is (x – 4), Quotient is (x² + 4x + 4) and Remainder is 3. Let’s find the Dividend = Divisor × + Remainder ]

Solution:

Given

In a division problem the Divisor is (x – 4), Quotient is (x2 + 4x + 4) and Remainder is 3.

Divisor (x – 4), Quotient (x2 + 4x + 4)

Remainder = 3

∴ Dividend = Divisor x Quotient + Remainder

= (x – 4) x (x² + 4x + 4) + 3 .

= x (x² + 4x + 4) -4 (x² + 4x + 4) + 3

= x³ + 4x² + 4x – 4x² – 16x – 16 + 3

= x³ – 12x – 13

Question 7. In a division problem, the divisor is (a² + 2a – 1), Quotient is 5a -14 and the remainder is 35a-17. Let’s find out and write the dividend.

Solution:

Given

In a division problem, the divisor is (a² + 2a – 1), Quotient is 5a -14 and the remainder is 35a-17.

Divisor is (a² + 2a – 1), Quotient is (5a – 14)

Remainder = 35a – 17

Divisor x Quotient + Remainder

= (a² + 2a – 1) (5a – 14) + (35a- 17)

= 5a (a² + 2a – 1) -14 (a² + 2a – 1) + 35a – 17

= 5a³ + 10a² – 5a – 14a² – 28a + 14 + 35a – 17

= 5a³– 4a²+ 2a – 3

“WBBSE Class 8 Chapter 4 Maths, Polynomials step-by-step solutions”

Question 8. Let’s write the quotient and the remainder.

1. (x² + 11x + 27) ÷ (x+6)

Solution:

Given

(x² + 11x + 27) and (x+6)

Quotient = (x+5), Remainder = -3

2. (81 x⁴+ 2) + (3x – 1)

Solution:

Given

(81 x⁴+ 2) and (3x – 1)

Quotient = (27×3+9x²+3x+1), Remainder = 3

3. (63x² – 19x – 20) + (9x² +5)

Solution:

Given

(63x² – 19x – 20) and (9x² +5)

Quotient = 7, Remainder = -19x-55

“WBBSE Maths Class 8 Multiplication and Division of Polynomials, Chapter 4 key concepts”

4. (x³-x²-8x-13) ÷ (x²+3x+3)

Solution:

Given

(x³-x²-8x-13) and (x²+3x+3)

Quotient = (x-4),Remainder = (x-1)

Pie Chart

This is the pictograph of how many clay dolls are made by Shahnaj’s father Niamat chacha (uncle) for the first 4 days of this week.

Let’s find answers to the questions from the pictograph.

1. Let’s write which day of the week Niamat chacha made the most number of clay dolls.

Solution: Wednesday

2. Let’s write how many clay dolls Niamat chacha made on Tuesday.

Solution: 90

“WBBSE Class 8 Maths Chapter 2 solutions, Pie Chart”

3. Let’s write which day of the week he made the least number of clay dolls.

Solution: Thursday

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

4. Let’s write how many clay dolls he made on Monday.

Solution: 80

Read and Learn More WBBSE Solutions For Class 8 Maths

To explain the data collected by me, my friend Amia made a bar diagram.

Number of clay dolls →

Let’s find the answers from the bardiagram of Amia.

1. Let’s write how many clay dolls Niamat chacha made on Monday.

Solution: 80

2. Let’s write when he made clay dolls least.

Solution: Thursday

3. Let’s write how many more clay dolls he made on Monday. than on Thursday.

Solution: 20

Let’s see in the bar diagram how many clay dolls Pritambabu and Amina Bibi made in first four days in the week.

Let’s see double columned bar diagram and find the answers to the questions below 

1. Let’s write between Pritambabu and Amina Bibi who made clay dolls most on Monday and how many clay dolls they made most.

Solution: On Monday Pritambabu made more clay dolls. Number of
more clay dolls made on Monday = (130 – 110) = 20

“Class 8 WBBSE Maths Chapter 2 solutions, Pie Chart study material”

2. Let’s write on which days of the week Amina Bibi more clay dolls from Pritambabu and how many more clay dolls did she make.

Solution: On Wednesday and Thursday Amina Bibi made more clay dolls than Pritambabu. Number of more clay dolls on Wednesday = (125-85) = 40

Number of more clay dolls on Thursday = (95 – 90) = 5

Pie Chart Exercise

In this year we have arranged to explain the making of various types of science models in the science exhibition of our school. Every day students of many schools and the guardians are coming to see in huge number. Let’s list those who have come in the exhibition today from 10 am to 12 noon on Sunday.

Let, Women – W

Men – M

Boy- B

Girl – G

[B, G, B, M, G, G, M, B, W, B, W, G, W, G, G, M, M, W, B, B, B, W, W, G, G, W, B, M, M, B, G, G,.B, W, M, M, W, M, M, G, G, W, M]

Let’s make a frequency table by the raw data using tally marks and make a bar diagram.

Solution: Frequency table

Bar diagram:

Ayan made a list of the hobbies of 30 students in our class:

Meher made a bar diagram of the data above.

The data is expressed through the circular regional picture beside. We see the sectors of reading and drawing are the largest and same in size.

Again, the sector of reading story book and playing are the smallest and similar in size.

So one sector indicates one part of the data and the area of one sector along with the quantity of a part of the data is proportional.

During recess the part of the total students singing = \(\frac{7 \text { people }}{30 \text { people }}=\frac{7}{30}\)

During recess the part of total students drawing picture = \(\frac{7}{30}\)

But during recess the part of the total students reading story books = \(\frac{5}{30}=\frac{1}{6}\)

But during recess the part of the total students playing drama = \(\frac{1}{6}\)

And during recess the part of the students dancing = \(\frac{1}{5}\)

So, one sector of singing and drawing pictures fill up the \(\frac{14}{30}\) part of the total circular region.

“WBBSE Class 8 Maths Chapter 2, Pie Chart solved examples”

During recess, the sector of dancing fills up the \(\frac{1}{5}\) part of the total circular region.

What is the writing system of data through this circular picture called?

It is called pie chart or circular regional chart.

Let’s try to make the sectors proportional to different parts of the data.

Let’s see the chart below and understand the data.

The pie chart of running conveyance on road today from 11 am to 12 noon.

We see – 1 Most running Bus

2. Least running Cycle.

3. Let’s write 2 cars running equally in numbers.

Answer: Lorry and Taxi

4. Let’s write how many parts the sector of a running taxi is of the circular region?

Solution:

\(\frac{14}{100}=\frac{7}{50}\)

It has been raining heavily since this morning. So most of the students can not come to school. Tathagatha makes a pie chart of the numbers of students who are present and absent in his class.

We see most of the students of Tathagata’s class are j Present] [ Present / Absent ]

What part of the circular region is denoted by the sector absent?

Solution:

\(\frac{40}{100}=\frac{2}{5}\)

Let’s make a pie chart of the data given in the list. Let us convert the percentage into fraction.

Now when I divide a circular region into some sectors, whose central angles are 144°, 72°, 18°, 90°, 36°.

∠AOB = 90°, ∠BOC = 18°, ∠COD = 72°

∠DOE = 144°, ∠AOE = 36°

Question 1. Last year in the month of April, 23 days were denoted to academics in Rohit’s school. Rohit has wtitten the number of students present in those 23 days in his school.

 

Now I make the frequency chart with tally mark and make bar diagram with the help of this, chart

“WBBSE Class 8 Pie Chart solutions, Maths Chapter 2”

Solution:

Given

Last year in the month of April, 23 days were denoted to academics in Rohit’s school. Rohit has wtitten the number of students present in those 23 days in his school.

Frequency chart

Bar diagram:

Question 2. Now I also make a bar diagram showing how many students out of a total of 40 students help in their household work (in house) during holidays. Let’s see the bar diagram and try to find out the answers of various questions.

Solution:

1. Let’s write how many students of our class do domestic work every holiday from the bar diagram and for how long.

Solution :

1. 6 students do household work for 5 hours.
2. 14 students do the work for 4 hours.
3. 12 students do the work for 3 hours.
4. 8 students do the work for 2 hours.

“Class 8 WBBSE Maths Chapter 2, Pie Chart easy explanation”

2. Let’s write how many students help in their domestic work for maximum time.

Solution: 14 students

3. Let’s write how many students help in their domestic work for two hours on every holiday.

Solution: 8 students

Question 3. Let’s see the pie chart below and find the answers to the following questions.

1. Let’s write how many parts of the total circular region is the sector of the auidence of Folk song.

Solution:

\(20 \%=\frac{20}{100}=\frac{1}{5}\) part

2. Let’s write from the pie chart which type of songs has the most number of listeners.

Solution: Audience of modern songs is the most in number.

3. Let’s write which type of songs has the least number of listeners.

Solution: Audience of classical music is the least.

“WBBSE Class 8 Maths Chapter 2 solutions, Pie Chart PDF”

2. The pie-chart of what kind of programmers the audience likes :

1. Let’s write how many part of the total circular region is the sector of the audience who watch news in the pie chart.

Solution:

\(\frac{20^{\circ}}{100^{\circ}}=\frac{1}{5}\) part

2. Let’s write what kind of programme gets the most audience.

Solution: Entertainment based

3. Let’s write what kind of programme gets the least audience.

Solution: Information based

4. Let’s write how many parts of the total audience watch the programmes of sports. 90°

Solution: \(\frac{90^{\circ}}{360^{\circ}}=\frac{1}{4}\) part

Question 4. I write the percentage of marks which Shuvam has secured in the final examination of class V below

Solution:

Let’s make a pie chart of this information and write the central angle of each sector

Hindi = \(\frac{15}{100}=15 \%=\frac{15}{100} \times 360^{\circ}\) = 54°

English = \(\frac{20}{100}=20 \%=\frac{20}{100} \times 360^{\circ}\) = 72°

Maths = \(\frac{30}{100}=30 \%=\frac{30}{100} \times 360^{\circ}\) = 108°

Environment = \(\frac{15}{100}=15 \%=\frac{15}{100} \times 360^{\circ}\) = 54°

Physical Education = \(\frac{20}{100}=20 \%=\frac{20}{100} \times 360^{\circ}\) = 72°

∠AOB = 54°, ∠BOC = 72°, ∠COD = 108°, ∠DOE = 54°, ∠AOE = 72°

Question 5. There is a shop of Madhubabu in our locality. I made a list of various types of things that were being sold in his shop for a particular day.

Solution:

Given

There is a shop of Madhubabu in our locality. I made a list of various types of things which were being sold in his shop for a particular day.

Now I try to make a pie-chart based on the above information.

Hints: First convert into fractions.

Total number of things sold that day = Rs. (320 +100+160+140)= Rs. 720

∴ Common bread sold = \(\frac{320}{720}\) = \(\frac{4}{9}\)

In the circular region of my pie chart, the central angle of the sector selling Common bread = 360° x \(\frac{4}{9}\) = 4 x 40° = 160°.

“WBBSE Class 8 Maths Chapter 2, Pie Chart important questions”

In the same way, the central angle of selling Slice bread is = 50°

The central angle of the sector of selling Cake is = 80°

The central angle of the sector of selling Biscuits is = 70°

Let’s draw a pie chart myself.

Question 6. I have made a list of things of what the students of class VIII of both the sections like to do during their leisure. (One student can like only one subject).

Solution:

Let’s work out from this data what parts of the total students like which subjects.

Let’s find the central angle of each sector and make pie chart accordingly.

Answer: Total number of the students = 20 + 25 + 27 + 28 + 20 = 120

Song = \(\frac{20}{120}=\frac{1}{6}=\frac{1}{6} \times 360^{\circ}\) = 60

Poem = \(\frac{25}{120}=\frac{5}{24}=\frac{5}{24} \times 360^{\circ}\) = 75

Dancing = \(\frac{27}{120}=\frac{9}{40}=\frac{9}{40} \times 360^{\circ}\) = 81

Drama = \(\frac{28}{120}=\frac{7}{30}=\frac{7}{30} \times 360^{\circ}\) = 84

Drawing = \(\frac{20}{120}=\frac{1}{6}=\frac{1}{6} \times 360^{\circ}\) = 60

Question 7. I have made a model. I made a chart of expenditure of buying materials.

Solution:

Let’s make a pie chart with this information and write the central angle of the sectors.

Total expenditure = (9 + 12 + 25 + 6 + 8) = 60

Art paper = \(\frac{9}{60} \times 360^{\circ}\) = 54°

Sketch pen = \(\frac{12}{60} \times 360^{\circ}\) = 72°

Scissor = \(\frac{25}{60} \times 360^{\circ}\) = 150°

Colour ribbon =  \(\frac{6}{60} \times 360^{\circ}\) = 36°

Pitch board = \(\frac{8}{60} \times 360^{\circ}\) = 48°

Question 8. I made a list of the painters based on the likings of 450 spectators coming to an art exhibition one day.

Solution:

Let’s make a pie chart with this information and write the central angle of the sectors.

Jaminy Roy = \(\frac{150}{450} \times 360^{\circ}\) = 120°

Nandalal Basu = \(\frac{120}{450} \times 360^{\circ}\) = 96°

Chintamoni Kar = \(\frac{80}{450} \times 360^{\circ}\) = 64°

Ganesh Pain = \(\frac{100}{450} \times 360^{\circ}\) = 80°

Nandalal Bose Pie Chart:

Question 9. A chart was made by asking the name of the favourite season to a group of 180 boys.

Solution:

Let’s find the answers to the questions from the pie chart below.

1. Let’s write which season is liked by most of the students and how none liked it.

Solution: Most students like winter.

No of students = 72

2. Let’s write which sensor is liked by the least number of students..

Solution: The least number of students like Rainy season.

3. Let’s write how many students like summer.

Solution: 36 students like summer.

“Class 8 Maths Pie Chart solutions, WBBSE syllabus”

4. Let’s write which season is described by the smallest sector.

Solution: The smallest sector denotes rainy season.

5. Let’s see the pie chart and make two more new questions. Try to find answers to them.

1. How many people like rainy season ?

Solution: 18 persons like rainy season.

2. How many people like spring ?

Solution: 54 people like spring.

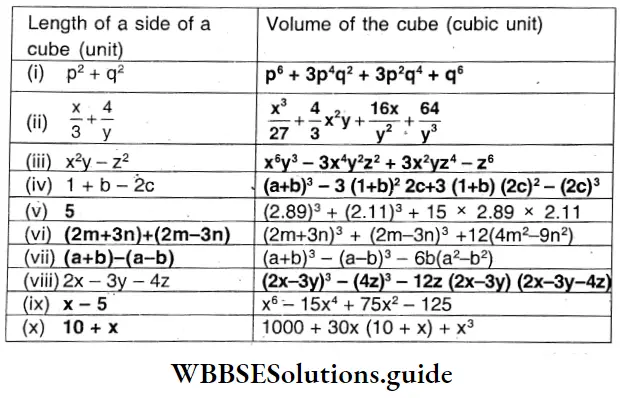
Algebraic Expression

In our village Asadpur, the school building will be repaired. This year the ex-students have decided to take over this duty. There are two rooms of different shapes in this school building. Tathagatha and I calculated the expenditure of repairing the room of class-l.

Question 1. After taking measurements of the room of class-l, it has been found that its length, breadth and height are 5 m, 4 m and 3 m respectively. Let us calculate how much money will be required to cement the floor at the rate of Rs. 55 per square metre.

Solution:

Given

After taking measurements of the room of class-l, it has been found that its length, breadth and height are 5 m, 4 m and 3 m respectively.

The area of the floor of that room (5 x 4) square metres = 20 square metres.

∴ The total cost for cementing the floor of that room will be

Rs. (20 x 55)

= Rs 1100

Rs 1100 will be required to cement the floor at the rate of Rs. 55 per square metre

Read and Learn More WBBSE Solutions For Class 8 Maths

Question 2. There is a door of dimension of 2 m x 1.4 m and there are 2 windows of the dimension of 1.3 m x 1.2 m in that room. Let’s find out how much it will cost to colour the 2 windows and 1 door at Rs. 42/ sq.m.

Solution:

Given

There is a door of dimension of 2 m x 1.4 m and there are 2 windows of the dimension of 1.3 m x 1.2 m in that room.

The area of the door = 2 m. x 1.4 m = 2.8 sq.m.

The area of a window the room = 1.3 m x 1.2m = 1.56

∴ The area of two windows = 2  1.56 sq.m = 3.12 sq.m.

∴ The total area of 1 door and 2 windows is = (2.8 + 3.12) sq.m.. = 5.92 sq.m.

“WBBSE Class 8 Maths Chapter 1 solutions, Algebraic Expression”

The total expenditure to colour the doors and windows at Rs. 42 sq.m, will be

= Rs. 5.92 × 42

= Rs.248.64

Rs.248.64 it will cost to colour the 2 windows and 1 door at Rs. 42/ sq.m

Question 3. Now let’s calculate the total expenditure if I whitewash four walls and the roof of this room at Rs. 6 sq.m.

Solution:

Including the door and windows, the area of 4 walls and roof is

= 2 x length x height + 2 x breadth x height + length x breadth

= (2x5x3 + 2x4x3 + 5 x 4) sq.m.

= (30 + 24 + 20) sq.m..

= 74 sq.m.

∴ The total area of 4 walls and roof without door and windows is

=  74  sq.m. 5.92 sq.m.

= 68.08 sq.m.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

The total expenditure to whitewash the four walls and the roof is

= Rs.  68.06 × 6 =Rs.  404.4

=Total expenditure = Rs. 404.48 +Rs. 248.64 + Rs.1000

= Rs. 1653.12

Total expenditure = Rs. 1653.12

Question 4. There is a rectangular shaped playground at the back of our school. The length of this playground is 40 meter and the breadth is 20 meter. A road having 3 meter width is there all around inside the playground. Let’s work out how much money will be required to construct the road at Rs. 95/sq.m.

Solution:

Given

There is a rectangular shaped playground at the back of our school. The length of this playground is 40 meter and the breadth is 20 meter. A road having 3 meter width is there all around inside the playground.

The area of the rectangular playground including the road is (40 x 20) sq.m. =  800 sq.m.

The length of the rectangular playground excluding the road is

= 40 metre -2 x 3 metre = (40 – 6) metre

= 34 metre

The breadth of the rectangular playground excluding the road is

= 20 metre -2 × 3 metre = (20 – 6) metre

= 14 meter

∴ The area of the rectangular playground excluding the road is

= 34 sq.m, x 14 sq.m.

= 476 sq.m.

∴ The area of the road is = 800 sq.m.-476 sq.m. = 324 sq.m.

∴ Total amount required to construct this road at rate of Rs. 95 per sq.m, is

= Rs.  324 × 95 = Rs. 30780

Rs. 30780 will be required to construct the road at Rs. 95/sq.m.

“Class 8 WBBSE Maths Chapter 1 solutions, Algebraic Expression study material”

Question 5. If there is road all around outside the ground of width 3 meter, then let us work out the expenditure of constructing the road at the same rate above (let’s do).

Solution:

Given

If there is road all around outside the ground of width 3 meter,

The area of the playground = 40 x 20 sq.m. = 800 sq.m.

Length of the playground including the road = (40 + 2 x 3) m.

= (40 + 6) m. = 46 m.

Breadth of the playground including the road = (20 + 2 x 3 ) m.

= (20 + 6) m. = 26 m.

Area of the playground including the road = 46 x 26 sq.m. = 1196 sq.m.

Area of the road =(1196 – 800) sq.m. = 396 sq.m..

The cost of constructing this road at the rate of Rs. 95 per sq.m.

= Rs. 396 x 95 = Rs. 37,620

The cost of constructing this road at the rate of Rs. 95 per sq.m. = Rs. 37,620

Funny game with coloured paper

Today some of us decided that we will cut rectangular and square shaped coloured papers and paste some black paper on that coloured paper to from roads of same width.

Question 6. Let’s see how much region of the coloured paper is black.

Solution:

Tirthanker draws:

Area of the paper with black road = 12 x 8 sq. cm.

= 96 sq. cm.

Area of the paper without the black road = 32 sq. cm.

∴ Area of the black road = 64 sq. cm.

We stick the two black roads in the middle of the green paper and so we get four green rectangular regions with same area.

Titli draws:

∴ Length of a green rectangular region = \(\frac{28-4}{2}\) cm. = 12  cm.

Breadth of a green rectangular region = \(\frac{18-4}{2}\)cm. = [7] cm

∴ Area of a green rectangular region = 12 × 7 sq. cm

=84 sq. cm

Area of 4 green rectangular regions with black road = 4 × 84 sq. cm

= 336 sq. cm

“WBBSE Class 8 Maths Chapter 1, Algebraic Expression solved examples”

= Area of big rectangular region with black road 28  x 18 sq. cm

= 504 sq. cm.

∴ Area of black road drawn by Titli = 504 – 336= 168 sq. cm.

Question 7. Area of black road drawn by Sophia 42 sq. cm.

Solution:

It is seen that the black coloured road divides the square region into four equal squares.

Question 8. Let’s see the pictures drawn by David, Farukh and Mitali and then let’s find the area of the black coloured roads and note it down.

Solution:

Area of the black coloured road drawn by David :

Area of the rectangular area= (13 + 5) × (16 + 5) sq. cm.

= 18 x 21 sq. cm. = 378 sq. cm.

Area of the land = 2 (13 x 8). sq. cm.

= 2 x 104 sq. cm.

= 208 sq. cm

Area of the road = (378 – 208) sq. cm = 170

Area of the black coloured road draw by Farukh :

Area of the region including the road 20 × 20 sq. cm. = 400 sq. cm.

Area of the region excluding the road = (20-12) × (20 – 12) sq. cm.

= 8 x 8 = 64 sq. cm.

Area of the road = (400 – 64) sq. cm. = 336 sq. cm.

Area of the black coloured road draw by Mitali

Area of the region including the road = 24 x 24 sq. cm. = 576 sq. cm.

Area of a pink sub-division = \(\left(\frac{24-4}{2}\right) \times\left(\frac{24-4}{2}\right)\) sq. cm.

= 10 x 10 sq. cm.

= 100 sq.cm.

Area of 4 pink regions = 4 x 100 sq. cm.

= 400 sq. cm.

∴ Area of the road = (576 – 400) sq. cm.

= 176 sq. cm.

Algebraic Expression Exercise

Question 1. Let’s see the pictures in the graph paper below and let’s find the area of the figures and note it down.

Solution:

Question 2. The length and breadth of the rectangular courtyard of the house of Amina are 6 m. and 4.2 m. respectively. We put a mattress of measure 3.5 m x 2.5 m in the middle of the courtyard. Let’s find the area of the courtyard except the mattress and note it down.

Solution:

Given

The length and breadth of the rectangular courtyard of the house of Amina are 6 m. and 4.2 m. respectively. We put a mattress of measure 3.5 m x 2.5 m in the middle of the courtyard.

Area of the courtyard = 6 × 4.2 sq. m. = 25.2 sq.m.

Area of the matress = 3.5 m. × 2.5 m. = 8.75 sq.m.

Area of the courtyard without the mattress = (25.2 – 8.75) sq.m. = 16.45 sq. m.

The area of the courtyard except the mattress = 16.45 sq. m.

Question 3. There is a path of 3 m width all around outside the square-shaped park of Ajanta Housing Complex. The perimeter of the park including the path is 484 m. Let’s calculate the area of the parth.

Solution:

Given

There is a path of 3 m width all around outside the square-shaped park of Ajanta Housing Complex. The perimeter of the park including the path is 484 m.

Perimeter of the square shaped park including the road = 484 m.

Length of one side of the square shaped park including the road = 484 ÷ 4 m. = 121 m.

Area of the park including the road = (121 )² sq.m = 14641 sq.m.

= (121-6) m. = 115 m.

Area of the park including the road = (115)² sq.m = 13225 sq.m.

∴ Area of the road = (14641 – 13225) sq.m = 1416 sq.m.

The area of the parth= 1416 sq.m.

Question 4. The length and breadth of Mihir’s rectangular garden are 50 meters and 30 meters respectively. There is a road in the middle of the garden of width 4 meter parallel to the length of the garden. This road divides the garden into two rectangular regions of equal area. Let’s draw a picture and find the area of the road and note it down.

Solution:

Given

The length and breadth of Mihir’s rectangular garden are 50 meters and 30 meters respectively. There is a road in the middle of the garden of width 4 meter parallel to the length of the garden. This road divides the garden into two rectangular regions of equal area.

1. If the road of width 4 m passing through the middle of the garden is parallel to the breadth and this road divides the garden into two equal parts, then let’s draw a picture and find the area of the road
   and note it down.
2.  If there are 2 roads of width 4 m parallel to the length and breadth of Mihir’s garden passing through the middle and divide the garden into 4 equal parts, then let draw a picture to find the area of the road and note it down.

Solution: Length of the rectangular garden including road = 50 m.

Breadth of the rectangular garden with road = 30 m.

Area of the rectangular garden with road = 50 × 30 sq.m =1500 sq.m

Breadth of the garden without the road = (30 – 4) m. = 26 m.

Area of the garden without the road = 50 × 26 sq.m= 1300 sq.m

Area of the road = (1500 – 1300)sq.m = 200 sq.m

Breadth of the garden without the road = (50 – 4) m. = 46 m.

Area of the garden without the road = 46 x 30 sq.m = 1380 sq.m

Area of the road = (1500 – 1380) sq.m = 120 sq.m

Area of the garden including the road = 50 x 30 sq.m = 1500 sq.m

Length of each part of the garden =  \(\frac{50-4}{2}\)m. = 23 m.

Breadth of each part of the garden = \(\frac{30-4}{2}\)m. = 13 m.

Area of each part of the garden = 23 x 13 sq.m – 299 m.

Area of all 4 parts of the garden without the road = 4 x 299 sq.m = 1196 sq.m

Area of the road = (1500 – 1196) sq.m = 304 sq.m

“WBBSE Class 8 Algebraic Expression solutions, Maths Chapter 1”

Question 5. There is a rectangular field beside our house owned by Papia’s family. The length and breadth of this land are 48 meter and 26 meter respectively. Papia’s family has built their house on that land leaving a 4 meter width gap on all sides. Let’s find the area of the region in which they have built their house.

Solution : 

Given

There is a rectangular field beside our house owned by Papia’s family. The length and breadth of this land are 48 meter and 26 meter respectively. Papia’s family has built their house on that land leaving a 4 meter width gap on all sides.

Area of the rectangular field = 48 x 26 sq.m = 1248 sq. m.

Length of the house = (48 – 2 x 4) m. = 40 m.

Breadth of the house = (26 – 2 x 4) m. = 18 m.

Area of the house = 40 x 18 sq.m = 720 sq.m

Papia will make her home at a field of measure 720 sq. m.

Arrange the colour sticks in different forms:

I am sticking match sticks along with Amita, Satyaki and Ayan on a white paper in different order. We shall hand up this in our classroom. Satyaki has decided to write the number of sticks after counting from each arrangement.

I arrange

Sattaki write –

Sattaki write –

Amita arranged

Sattaki write –

Algebraic Expression Exercise

Question 1. Let’s find the total number of matchsticks required in the n-th position of the previous types of arrangements.

Solution:

Activity

Let’s make some square and rectangular cards where one side of them is blue and the other side is red.

Like the above picture,

blue (4 cm x 4 cm) square card → x²

blue (4 cm × 1 cm) rectangular card → x

blue (1 cm × 1 cm) square card →1

and red (4 cm x 4 cm) square card → x²

red (4 cm x 1 cm ) rectangular card → x

red (1 cm x 1 cm) square card → 1

Let us express the algebraic expression with blue and red cards :

2x²+ 4x – 3

– 2x² + 2x – 1

2x² – 3x + 5

-x² -8x + 6

4x² – 2x – 3

– 4x² + 7x – 4

(x² + 2x + 5) + (2x² + 2x + 1)

(3x² – 5x + 6) + (2x² + 8x – 4)

(8x² – 2x – 4) – (3x² + 4x + 2)

(- 2x² + 5x + 3) – (-4x² + 2x -2)

Hints: 2x² + 4x – 3

New Game With Fun Cards:

Uma Samir, Sudir and I have decided that we will make some square and rectangular cards and will write length and breadth. We will pick up cards one by one and will write area or length or breadth of the cards.

Let’s see the length and breadth of my card which I picked up.

Area of the card = (2x + 4)m x(x – 5)m

= (2x + 4)(x – 5) sq.m.

= (2x²+ 4x – 10x – 20)sq.m = (2x²– 6x – 20) sq.m

Let’s see the length and breadth of Lima’s card-

Area of Uma’s card =5x – 7m × \(\frac{x}{5}+2\) m

= \(x^2+10 x-\frac{7 x}{5} 14\) sq.m

However, area of Samir’s card is (7a2b – 35ab2 + 14abc) sq.m and breadth is 7ab m.

∴ Length of Samir’s card

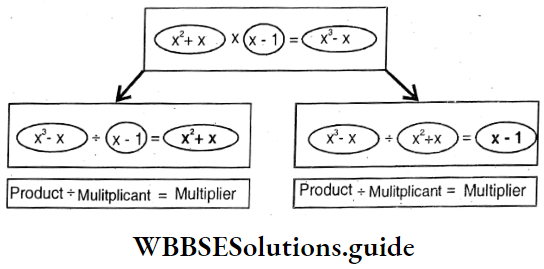
= (7a²b – 35ab² + 14abc) sq. m. ÷ 7ab m.

= \(\left(\frac{{ }^a 7 a^2 b}{7 a b}-\frac{{ }^{5 b} 35 a b^2}{7 a b}+\frac{{ }^{2 c} 14 a b c}{7 a b}\right) m .\)

= (a – 5b + 2c) m.

Area of Subir’s card is (6x⁴y⁴ — 12x²y² + 30x²y⁴) sq. m. and length is 6x²y² metre.

Breadth of the card = 6x⁴y⁴ – 12x²y² + 30x²y⁴ sq. m. ÷ 6x²y²m.

= \(\frac{6 x^4 y^2-12 x^2 y^2+30 x^2 y^4}{6 x^2 y^2}\)

= \(\frac{6 x^4 y^2}{6 x^2 y^2}-\frac{12 x^2 y^2}{6 x^2 y^2}+\frac{30 x^2 y^4}{6 x^2 y^2}\)

= (x² – 2 + 5y²) m.

“Class 8 WBBSE Maths Chapter 1, Algebraic Expression easy explanation”

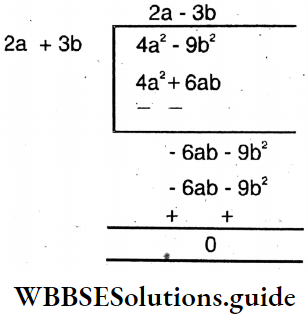
Let’s find the length of the card where the area of the card is (9p²-4q²) sq.m and breadth of the card is (3p-2q) m.

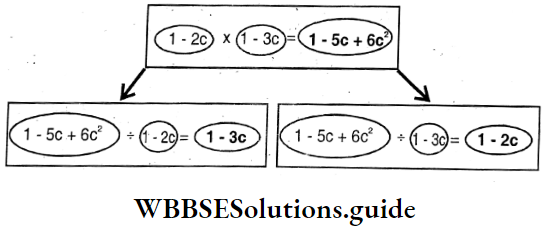
Solution : Length = Area ÷ Breadth = \(\frac{9 p^2-4 q^2}{3 p-2 q}\)

Let’s express 9p2 – 4q2 into product of two expressions, i.e., factorise it. ,

9p² – 4q² = (3p)² – (2q)²

= (3p + 2q)(3q – 2q)

∴ Length = \(\frac{9 p^2-4 q^2}{3 p-2 q}\) metre

= \(\frac{(3 p+2 q)(3 p-2 q)}{(3 p-2 q)}\)

= (3p + 2q) metre

Algebraic Expression Exercise

Length of the rectangular card And Breadth of the rectangular card:

Algebraic Expression Exercise

Question 1. Let’s write the number of matchsticks in the n-th position (n is a positive integer) in the arrangement :

Solution:

1. Figure …………5n + 1
2. Figure …………..5n + 2
3. Figure …………….4n + 1

Question 2. Let’s write the perimeter of an equilateral triangle if length of each side is (4y + 2) cm.

Solution:

Perimeter of an equilateral triangle = 3 x side cm.

= 3(4y + 2) cm.

= 12y + 6 cm.

Perimeter of an equilateral triangle = 12y + 6 cm.

Question 3. Let’s write the area of the rectangular region whose length is (8x + 3y) cm and breadth is (8x – 3y) cm.

Solution:

Area of the rectangular region = (8x + 3y)cm × (8x – 3y) cm.

= (8x + 3y) (8x – 3y) sq. cm.

= (8x)² – (3y)² sq. cm.

= (64x² – 9y²) sq.cm.

Area of the rectangular region = (64x² – 9y²) sq.cm.

Question 4. Let’s write the area of the square region in terms of m where length is (3m – 4) metre. Let’s calculate the value of m when the perimeter of the square is 8 metre.

Solution:

Area of the square = (3m – 4) m. × (3m – 4) m.

= (3m – 4)² sq. m.

= (3m)² – 2.3m.4 + (4)² sq m.

= (9m²– 12m + 16) sq. m.

The perimeter of the square =4 x (3m – 4) m.

= 12m – 16 metre.

According to the problem,

12m -16 = 8

or, 12m = 8+16

or, 12m = 24

or, m= \(\frac{24}{2}\) = 2

If m is 2, perimeter will be 8 m

The value of m is 2 when the perimeter of the square is 8 metre

“WBBSE Class 8 Maths Chapter 1 solutions, Algebraic Expression PDF”

Question 5. Let’s fill up the table below:

Solution :

1. Algebraic expression

x²+2y²……………… (1)

(-8y²+ 6x²+z²)……………… (2)

Let’s add:

(1 + 2) equations adding:

x²+2y² + (-8y²+6x²+z²)

= x²+2y²-8y²+6x²+z²

= 7x²-6y²+z²

Let’s Subtract: 

(1- 2) Equations substract:

x²+2y²-(-8y²+6x²+z²)

= x²+2y²+8y²-6x²-z²

= 10y²-5x²-z²

2. Algebraic expression

6a²+2 …………..(1)

-3a²+3a……….(2)

-2a+3…………….(3)

(1+2+3) equations adding:

= (6a²+2) + (-3a²+3a) + (-2a+3)

= 6a²+2 – 3a² + 3a -2a+3

= 3a² + a +5

(2-1) Equations subtract:

= (-3a²+3a) – (6a²+2)

= -3a²+3a – 6a² – 2

= – 9a² + 3a – 2

(3-1) Equations subtract:

= (-2a+3) – (6a²+2)

= -2a + 3 – 6a² – 2

= -6a² – 2a + 1

3. Algebraic expression.

9m²-2mn+n²………..(1)

m²+n²…………..(2)

m²-3mn-2n²…………..(3)

(1+2+3) equations adding:

= (9m²-2mn+n²) + (m²+n²) + (m²-3mn-2n²)

= 9m²-2mn+n² + m²+n² + m² – 3mn – 2n²

= 11m² – 5mn

(1-2) equations subtract:

= (9m²-2mn+n²) – (m²+n²)

= 9m²-2mn + n² – m² -n²

= 8m² – 2mn

“WBBSE Class 8 Maths Chapter 1, Algebraic Expression important questions”

(2-3) equations subtract:

= (m²+n²) – (m²-3mn-2n²)

= m²+n² – m² + 3mn + 2n²

= 3n² + 3mn

Question 6. Let’s fill up the table below

Solution :

1. Algebraic expression

9a³b²-15a²b³………….(1)

3ab………………….(2)

(1 × 2) equations multiply:

(9a³b²-15a²b³)x3ab

= 27a³⁺¹b2+1-45a²⁺¹b³⁺¹

= 27a⁴b³-45a³b⁴

(1÷2) equation divided:

= \(\frac{9 a^3 b^2-15 a^2 b^3}{3 a b}\)

= \(\frac{9 a^3 b^2}{3 a b}-\frac{15 a^2 b^3}{3 a b}\)

\(=3 a^{3-1} b^{2-1}-5 a^{2-1} b^{3-1}\)

= \(3 a^2 b-5 a b^2\)

2. Algebraic expression

x⁴-4x³+6x²………….(1)

x²………………………(2)

(1 × 2) equations multiply:

(x⁴-4x³+6x²) x x²

= x⁴⁺²– 4x³⁺²+ 6x²⁺¹

= x⁶ – 4x⁵+ 6x⁴

(1÷2) equation divided:

= \(\frac{x^4-4 x^3+6 x^2}{x^2}\)

= \(\frac{x^4}{x^2}-\frac{4 x^3}{x^2}-\frac{6 x^2}{x^2}\)

= \(x^{4-2}-4 x^{3-2}+6 x^{2-2}\)

= x² – 4x + 6

3. Algebraic expression

3m²n³+40m³n⁴-5m⁴n5……………(1)

10m²n²……………..(2)

(1 × 2) equations multiply:

(3m²n³+40m³n⁴-5m⁴n⁵) x 10m²n²

= 30m⁴n⁵+40m⁵n⁶-50m⁶n7

(1÷2) equation divided:

(3m²n³+40m³n⁴-5m⁴n⁵) ÷ 10m²n²

= \(\frac{3 m^2 n^3+40 m^3 n^4-5 m^4 n^5}{10 m^2 n^2}\)

= \(\frac{3 m^2 n^3}{10 m^2 n^2}+\frac{40 m^3 n^4}{10 m^2 n^2}-\frac{5 m^4 n^5}{10 m^2 n^2}\)

= \(\frac{3}{10} n+4 m n^2-\frac{1}{2} m^2 n^3\)

4. Algebraic expression

(49l²-100m²) + 10m)……………….(1)

(7I + 10m)………………. (2)

(1 × 2) equations multiply:

(49l²-100m²) x (7l + 10m)

343l³-700m²l+490ml²-1000m³

(1÷2) equation divided:

(49l²-100m²) ÷ (7l+10)

= \(\frac{\left.49\right|^2-100 m^2}{7 I-10 m}\)

= \(\frac{(7 \mathrm{l})^2-(10 m)^2}{7 \mathrm{I}-10 \mathrm{~m}}\)

= \(\frac{(7 \mathrm{I}+10 \mathrm{~m})(7 \mathrm{I}-10 \mathrm{~m})}{(7 \mathrm{I}-10 \mathrm{~m})}\)

= (71 + 10m)

4. Algebraic expression

625a⁴-81b⁴………………..(1)

5a+3b……………….(2)

(1 × 2) equations multiply:

= (625a⁴-81 b⁴) x (5a+3b)

= 3125a⁵-40⁵ab⁴+1875a⁴b-243b⁵

“Class 8 Maths Algebraic Expression solutions, WBBSE syllabus”

(1÷2) equation divided:

(625a⁴-81b⁴) ÷ (5a+3b)

= \(\frac{625 a^4-81 b^4}{5 a+3 b}\)

= \(\frac{\left(25 a^2\right)^4-\left(9 b^2\right)^4}{(5 a+3 b)}\)

= \(\frac{\left(25 a^2+9 b^2\right)\left(25 a^2-9 b^2\right)}{(5 a+3 b)}\)

= (25a2 + 9b2)(5a – 3b)

= 125a3 – 75a2b + 45ab2 – 27b3

Question 7. Let’s simplify :

1. (a-b) + (b-c) + (c-a)

Solution : (a-b) + (b-c) + (c-a)

=a – b + b – c + c – a

= 0

(a-b) + (b-c) + (c-a) = 0

2. (a+b)(a-b) + (b+c)(b-c) + (c+a)(c-a)

Solution:

(a+b)(a-b) + (b+c)(b-c) + (c+a)(c-a)

= a² – b² + b² – c²+ c² – a²

= 0

(a+b)(a-b) + (b+c)(b-c) + (c+a)(c-a)= 0

3.  \(x^2 \times\left(\frac{x}{y}-\frac{y}{x}\right) \times\left(\frac{y}{x}+\frac{x}{y}\right) \times y^2\)

Solution:

= \(x^2 \times\left(\frac{x}{y}-\frac{y}{x}\right) \times\left(\frac{y}{x}+\frac{x}{y}\right) \times y^2\)

= \(x^2 \times\left(\frac{x^2-y^2}{x y}\right) \times\left(\frac{y^2+x^2}{x y}\right) \times y^2\)

= \(\frac{x^2 \times\left(x^2-y^2\right) \times\left(x^2+y^2\right) \times y^2}{x^2 y^2}\)

= \(\left(x^2\right)^2-\left(y^2\right)^2\)

X⁴– Y⁴

4. a(b-c) + b(c-a) + c(a-b)

Solution :

a(b-c) + b(c-a) + c(a-b)

= ab – ac + be – ab + ac – be

= 0

a(b-c) + b(c-a) + c(a-b) = 0

5. x²(y²-z²) + y²(z²-x²) + z²(x²-y²)

Solution :

= x²(y²-z²) + y²(z²-x²) + z²(x²-y²)

= x²y² – x²z² + y²z² – x²y² + x²z² – y²z²

= 0

x²(y²-z²) + y²(z²-x²) + z²(x²-y²)= 0

“WBBSE Class 8 Chapter 1 Maths, Algebraic Expression step-by-step solutions”

6. (x³+y³)(x³-y³) + (y³+z³)(y³-z³) + (z³+x³)(z³-x³)

Solution :

= (x³+y³)(x³-y³) + (y³+z³)(y³-z³) + (z³+x³)(z³-x³)

= (x³)² – (y³)² + (y³)² – (z³)² + (z³)²– (x³)²

= x⁶-y⁶ +y⁶-z⁶+z⁶-x⁶

= 0

(x³+y³)(x³-y³) + (y³+z³)(y³-z³) + (z³+x³)(z³-x³)

(a+b) ²= a² + 2ab + b² and (a-b)² = a² – 2ab + b²

Question 8. Let’s form a whole square of the expressions given below usingthe above given identities –

1. 5x-2y
2. 7+2m
3. x+y+z
4. a+b-c-d

1. 5x-2y

Solution:

= (5x-2y)²

= (5x)²– 2.5x.2y + (2y)²

= 25x² – 20xy + 4y²

(5x-2y)²= 25x² – 20xy + 4y²

2. 7+2m

Solution:

= (7+2m)²

= (7)² + 2.7.2m + (2m)²

= 49 + 28m + 4m2

(7+2m)²  = 49 + 28m + 4m2

3. x+y+z

Solution:

= (x+y+z)²

= {(x+y)+z}²

= (x+y)²+2(x+y).z+(z)²

= x²+2xy+y²+2xz+2yz+z² .

= x²+y²+z²+2xy+2xz+2yz

x+y+z)² = x²+y²+z²+2xy+2xz+2yz

4. a+b-c-d

Solution:

= (a+b-c-d)²

= {(a+b) – (c+d)}²

= (a+b)²-2(a+b)(c+d)+(c+d)²

= a²+2ab+b²-2a(c+d)-2b(c+d)+c²+2cd+d²

= a²+2ab+b²-2ac-2ad-2bc-2bd+c²+2cd+d²

= a²+b²+c²+d²+2ab-2ac-2ad-2bc-2bd

(a+b)² = a² + 2ab + b² and (a-b)² = a²– 2ab + b²

(a+b-c-d)² = a²+b²+c²+d²+2ab-2ac-2ad-2bc-2bd

Question 9. Let’s form whole squares of the expressions given below using the above identities.

1.  \(9 x^2+\frac{9}{25 y^2}-\frac{18 x}{5 y}\)
2. 25m²-70mn+49n²
3. (2a-b)2+(4a-2b)(a+b)+(a+b)2
4. \(\frac{p^2}{q^2}+\frac{q^2}{p^2}-2\)

1. \(9 x^2+\frac{9}{25 y^2}-\frac{18 x}{5 y}\)

Solution:

= \((3 x)^2+\left(\frac{3}{5 y}\right)^2-2.3 x \cdot \frac{3}{5 y}\)

= \(\left(3 x-\frac{3}{5 y}\right)^2\)

2. 25m²-70mn+49n²

Solution:

Given 25m²-70mn+49n²

= (5m)²-2.5m.7n+(7n)²

= (5m-7n)²

25m²-70mn+49n² = (5m-7n)²

3. \(\frac{p^2}{q^2}+\frac{q^2}{p^2}-2\)

Solution:

Given \(\frac{p^2}{q^2}+\frac{q^2}{p^2}-2\)

= \(\left(\frac{p}{q}\right)^2+\left(\frac{q}{p}\right)^2-2 \cdot \frac{p}{q} \cdot \frac{q}{p}\)

= \(\left(\frac{p}{q}-\frac{q}{p}\right)^2\)

Question 10. Let’s express the expression as a difference of two squares :

1. 391× 409

Solution:

Given 391 x 409

= (400-9)(400+9)

= (400)²-(9)²

2. (4x+3y)(2x-3y)

Solution:

Given (4x+3y)(2x-3y)

= 8x²-12xy+6xy-9y²

= 8x²-6xy-9y²

=9x²-x²-6xy-9y²

=9×2-(x²+6xy+9y²)

=(3x)²-(x+3y)²

3. X

Solution:

Given X

= X x 1

= \(\left(\frac{x+1}{2}\right)^2-\left(\frac{x-1}{2}\right)^2\)

“WBBSE Maths Class 8 Algebraic Expression, Chapter 1 key concepts”

Question 11. Let’s factorize :

1. 225m²-100n²

Solution:

Given 225m²-100n²

= 25 (9m² – 4n²)

= 25 {(3m)² – (2n)²}

= 25 (3m + 2n) (3m – 2n)

225m²-100n² = 25 (3m + 2n) (3m – 2n)

2. 25x² – \(\frac{1}{9}\) y²z²

Solution:

Given 25x² – \(\frac{1}{9}\) y²z²

= (5x)2 – \(\left(\frac{1}{3} y z\right)^2\)

= (5x + \(\frac{1}{3}\)yz)(5x- \(\frac{1}{3}\) yz)

3. 7ax² + 14ax + 7a

Solution:

Given 7ax² + 14ax + 7a

= 7a (x² + 2x + 1).

= 7a {(x)² + 2.x.1 + (1)²}

= 7a (x + 1 )²

7ax² + 14ax + 7a = 7a (x + 1 )²

4. 3x⁴ – 6x²a² + 3a⁴

Solution:

Given 3x⁴ – 6x²a² + 3a⁴

= 3 (x⁴ – 2x²a² + a⁴) .

= 3 {(x²)² – 2.x².a² + (a²)²}

= 3 (x² – a²)²

= 3 {(x + a) (x – a)}²

= 3 (x + a)² (x – a)²

3x⁴ – 6x²a² + 3a⁴ = 3 (x + a)² (x – a)²

“WBBSE Class 8 Maths Chapter 1, Algebraic Expression summary”

5. 4b²c² – (b² + c² – a²)²

Solution:

Given 4b²c² – (b² + c² – a²)²

= (2bc)² – (b² + c² – a²)² = (2bc + b² + c² – a²) (2bc – b² – c² + a²)

= (b² + 2bc + c² – a²) (a² – b² + 2bc – c²)

= {(b + c)² – (a)²} {a²– (b² – 2bc + c²)}

= {(b + c)² – (a)²} {(a)² – (b-c)²}

= (b + c + a) (b + c – a) (a + b – c) (a – b + c)

4b²c² – (b² + c² – a²)² = (b + c + a) (b + c – a) (a + b – c) (a – b + c)

“WBBSE Class 8 Maths Chapter 1 Algebraic Expression, definitions and formulas”

6. 64ax² – 49a (x – 2y)²

Solution:

Given 64ax² – 49a (x – 2y)²

= a {64x² – 49 (x – 2y)²}

= a [64x² – {7(x – 2y)}²]

= a {(8x)² – (7x – 14y)²}

= a (8x + 7x – 14y) (8x – 7x + 14y)

= a (15x – 14y) (x + 14y)

64ax² – 49a (x – 2y)² = a (15x – 14y) (x + 14y)

7. x² – 9 – 4xy + 4y²

Solution:

Given x² – 9 – 4xy + 4y²

= x² – 4xy + 4y² – 9

= (x)² – 2.x.2y + (2y)² – 9

= (x – 2y)² – (3)²

= (x – 2y + 3) (x – 2y – 3)

x² – 9 – 4xy + 4y² = (x – 2y + 3) (x – 2y – 3)

8. x² – 2x – y² + 2y

Solution:

Given x² – 2x – y² + 2y

= x² – y² – 2x + 2y

= (x + y) (x – y) – 2(x – y)

= (x – y) (x + y – 2)

x² – 2x – y² + 2y = (x – y) (x + y – 2)

9. 3 + 2a – a²

Solution:

Given 3 + 2a – a²

= 4-1 + 2a – a²

= 4 – (1 – 2a + a2)

= (2)² – {(1 )2 – 2.1 .a + (a)²}

= (2)2 – (1 – a)2

= (2 + 1 – a) (2 – 1 + a)

= (3 – a) (1 + a)

3 + 2a – a² = (3 – a) (1 + a)

10. X⁴– 1

Solution:

Given X⁴– 1

= (x2)²-(1)²

= (x²+ 1) (X²– 1)

= (X²+ 1) {(X)² – (1)²}

= (x²+1) (x+1) (x-1)

X⁴– 1 = (x²+1) (x+1) (x-1)

11. a² – b² – c² + 2bc

Solution:

Given a² – b² – c² + 2bc

= a² – (b² – 2bc + c²)

= (a)² – (b – c)²

= (a + b – c) (a – b + c)

a² – b² – c² + 2bc = (a + b – c) (a – b + c)

12. ac + be + a + b

Solution:

Given ac + be + a + b

= c (a + b) + 1 (a + b)

= (a + b) (c + 1)

ac + bc + a + b = (a + b) (c + 1)

“WBBSE Class 8 Maths Algebraic Expression, revision notes”

13. x⁴+ x²y² + y⁴

Solution:

Given x⁴+ x²y² + y⁴

= (x²)² + 2.x²y² + (y²)² – x²y²

= (x² + y²) – (xy)²

= (x² + y² + xy) (x² + y² – xy)

= (x² + xy + y²) (x² – xy + y²)

x⁴+ x²y² + y⁴ = (x² + xy + y²) (x² – xy + y²)

Question 12. Let’s find the product by formulae:

1. (xy + pq) (xy – pq)

Solution:

Given (xy + pq)(xy – pq)

= (xy)² – (pq)²

= x²y² – p²q²

(xy + pq) (xy – pq) = x²y² – p²q²

2. 49 x 51

Solution:

Given 49 x 51

= (50- 1) (50 + 1)

= (50)2 – (1)2

= 2500 – 1

= 2499

49 x 51 = 2499

3. (2x – y + 3z) (2x + y + 3z)

Solution:

Given

= (2x + 3z – y) (2x + 3z + y)

= (2x + 3z)² – (y)²

= (2x)² + 2.2x.3z + (3z)² – y²

= 4x² + 12xz + 9z² – y²

(2x – y + 3z) (2x + y + 3z) = 4x² + 12xz + 9z² – y²

4. 1511 x 1489

Solution:

Given 1511 x 1489

= (1500 + 11) (1500 – 11)

= (1500)² – (11)²

= 2250000 – 121

= 2249879

1511 x 1489 = 2249879

5. (a – 2) (a + 2) (a² + 4)

Solution:

Given (a – 2) (a + 2) (a² + 4)

= {(a)² – (2)²} (a² + 4)

= (a² – 4) (a² +4)

= (a²)² – (4)²

= a⁴– 16

(a – 2) (a + 2) (a² + 4) = a⁴– 16

Question 13. (1). If x+\(\frac{1}{x}\)=4 then let’s show that x²+\(\frac{1}{x^2}\) and X⁴+\(\frac{1}{x^4}\)=194.

Solution:

= \(x+\frac{1}{x}=4\)

=\(x^2+\frac{1}{x^2}\)

=\((x)^2+\left(\frac{1}{x}\right)^2\)

=\(\left(x+\frac{1}{x}\right)^2-2 \cdot x \cdot \frac{1}{x}\)

=(4)²-2

=16-2

=14

Again, \(x^4+\frac{1}{x^4}\)

=\(\left(x^2\right)^2+\left(\frac{1}{x^2}\right)^2\)

=\(\left(x^2+\frac{1}{x^2}\right)^2-2 \cdot x^2 \cdot \frac{1}{x^2}\)

=(14)²-2

=196-2

=194

2. If m+\(\frac{1}{m}\)=-5 then lets show that m²+\(\frac{1}{\mathrm{~m}^2}\)=23.

Solution: m+\(\frac{1}{m}\)=-5

= \(m^2+\frac{1}{m^2}\)

=\((m)^2+\left(\frac{1}{m}\right)^2\)

=\(\left(m+\frac{1}{m}\right)^2-2 \cdot m \cdot \frac{1}{m}\)

=(-5)²-2

=25-2

= 23

3. If p-\(\frac{1}{p}\)=m then let’s show that:

Solution:

1. p² +\(\frac{1}{p^2}\)= m² + 2; and,
2. \(\left(p+\frac{1}{p}\right)^2=m^2+4\)

p-\(\frac{1}{p}\) = m

1. \(p^2+\frac{1}{p^2}\)

Solution:

Given \(p^2+\frac{1}{p^2}\)

= \((p)^2+\left(\frac{1}{p}\right)^2\)

= \(\left(p+\frac{1}{p}\right)^2+2 \cdot p \cdot \frac{1}{p}\)

= (m)²+2

= m²+2

2. \(\left(p+\frac{1}{p}\right)^2\)

Solution:

Given \(\left(p+\frac{1}{p}\right)^2\)

= \(\left(p-\frac{1}{p}\right)^2+4 \cdot p \cdot \frac{1}{p}\)

= (m)2+4

= m2+4

3. If a + b = 5, a – b = 1 then let’s show that 8ab(a² + b²) = 624.

Solution :

= 8ab(a² + b²)

= 4ab. 2(a² + b²)

= {(a+b)²-(a-b)²}{(a+b)²+(a-b)²}

= {(5)²-(1)²}{(5)² + (1)²}

= (25-1) (25 + 1)

= (25)²-(1)²

= 625-1

= 624

8ab(a² + b²) = 624

4. If x – y = 3, xy = 28 then let’s find the value of (x² + y²).

Solution :

= x² + y²

= (x – y)² + 2xy

= (3)² + 2.28

= 9 + 56

= 65

(x² + y²) = 65

Question 14. Let’s express the expressions as the sum of two squares:

1. 2(a² + b²)
2. 50x²+18y²
3. a² + b² + c² + d²+ 2(ac -bd)

1. 2 (a² + b²)

Solution:

Given 2 (a² + b²)

= (a + b)² + (a – b)²

2. 50 x² + 18 y²

Solution:

Given 50 x² + 18 y²

= 2 (25x² + 9y²)

= 2 {(5x)² + (3y)²}

= (5x + 3y)² + (5x – 3y)²

3. a² + b² + c² + d² + (ac -bd)

Solution:

Given a² + b² + c² + d² + (ac -bd)

= a² + b² + c² + d² + 2ac – 2bd

= a² + 2ac + c² + b² – 2bd + d²

= (a + c)² + (b – d)²

Question 15.

Solution :

1. Let’s write for which value of t, x² – tx + \(\frac{1}{4}\) will be a whole square form.
2. Let’s write the expression which when added to a² + 4, gives a whole square.
3. If a and b are positive integers and a² – b² = 9 x 11, then let’s write the value of a & b.
4. Let’s write logically whether (x + y)² – (x – y)² = 4xy is an identity or an equation.
5. For each positive or negative value of x and y except zero, the value of (x² + y²) is always ( positive or negative ).

1.  x² – tx + \(\frac{1}{4}\)

= \((x)^2-t x+\left(\frac{1}{2}\right)^2\)

( ∴ 2ab = 2.x. \(\frac{1}{2}\) = x)

or, If =1 then x² – x + \(\frac{1}{4}=\left(x-\frac{1}{2}\right)^2\)

or, If = -1 then x² – (-1)x +\(\frac{1}{4}\)

= \(x^2+x+\frac{1}{4}\)

= \(\left(x+\frac{1}{2}\right)^2\)

The value of t being 1 or -1, x² – tx + \(\frac{1}{4}\) will be a whole square.

2. a² + 4

Solution :

Given a² + 4

= (a)² + (2)²

= (a + 2)² – 2.a.2.

= (a + 2)² – 4a

a² + 4 3 4a

3. a²– b2 = 9 x 11

Solution :

Given a²– b2 = 9 x 11

= (a + b) (a – b)

= (10 + 1) (10 -1)

or a = 10 and b = 1 then this equation will be established.

∴ a = 10, b= 1

4. (x + y)² – (x – y)² = 4xy

Solution :

Given (x + y)² – (x – y)² = 4xy

L.H.S = (x + y)²– (x -y)²

= x2 + 2xy + y² – (x² – 2xy + y²)

= x2 + 2xy + y² – (x² + 2xy + y²)

= 4xy

= R.H.S

∴ L.H.S = R.H.S.

∴ This is an identity.

5. Find for each positive or negative value x and y, except zero, the value of (x² + y²).

Question 16. Let’s solve :

1. 6x = 72

2. 9x + 2 = 20

3. 4x – 2x + 3 = 9 – 4x

4. \(\frac{x}{4}-\frac{x}{2}=3 \frac{1}{2}-\frac{x}{3}\)

5. 2x – 5 { 7 – (x – 6) + 3x } – 28 = 39

6. \(\frac{1}{3}\) (x-2) + \(\frac{1}{4}\) (x+3)= \(\frac{1}{5}\) (x+4) + 15

1. 6x = 72

Solution :

Given 6x = 72

or, x = \(\frac{72}{6}\)

or, x = 12

2. 9x + 2 = 20

Solution:

Given 9x + 2 = 20

or, 9x = 20 – 2

or, 9x = 18

or, x = \(\frac{18}{9}\)

or, x = 2

“Class 8 WBBSE Maths Chapter 1 Algebraic Expression, multiple-choice questions”

3. 4x – 2x + 3 = 9 – 4x

Solution:

Given 4x – 2x + 3 = 9 – 4x

or, 4x – 2x + 4x = 9 – 3

or, 8x – 2x = 6

or, 6x = 6

or, x = \(\frac{6}{6}\)

or, x = 1 Ans.

4. \(\frac{x}{4}-\frac{x}{2}=3 \frac{1}{2}-\frac{x}{3}\)

Solution :

Given \(\frac{x}{4}-\frac{x}{2}=3 \frac{1}{2}-\frac{x}{3}\)

or, \(\frac{x}{4}-\frac{x}{2}+\frac{x}{3}=\frac{7}{2}\)

or, \(\frac{3 x-6 x+4 x}{12}=\frac{7}{2}\)

or, \(\frac{7 x-6 x}{12}=\frac{7}{2}\)

or, \(\frac{x}{12}=\frac{7}{2}\)

or, \(x=\frac{7}{2} \times{ }^6 \not 2\)

or, x = 42 Ans.

5. 2x – 5 { 7 – (x – 6) + 3x} – 28 = 39

Solution:

Given 2x – 5 { 7 – (x – 6) + 3x} – 28 = 39

or, 2x – 5 (7 – x + 6 + 3x) – 28 = 39

or, 2x – 5 (2x + 13) -28 = 39

or, 2x – 10x – 65 – 28 = 39

or, – 8x = 39 + 65 + 28

or, -8x = 132

or, x = \(\frac{132}{-8}\)

or, x = \(-\frac{33}{2}=-16 \frac{1}{2}\) Ans.

6. \(\frac{1}{3}(x-2)+\frac{1}{4}(x+3)=\frac{1}{5}(x+4)+15\)

Solution:

Given \(\frac{1}{3}(x-2)+\frac{1}{4}(x+3)=\frac{1}{5}(x+4)+15\)

or, \(\frac{(x-2)}{3}+\frac{(x+3)}{4}-\frac{(x+4)}{5}=15\)

or, \(\frac{20(x-2)+15(x+3)-12(x+4)}{60}=15\)

or, 20x – 40 + 15x + 45 – 12x – 48 = 900

or, 35x – 12x = 900 + 40-45 + 48

= 23x = 988 – 45

or, 23x = 943

or, x = \(\frac{943}{23}\)

or, x = 41 Ans.

Algebraic Expression Geometric figures

Today we will play a game. We friends collect two blackboards. One of our friends will write several conditions and others will try to draw different geometrical figures according to the given conditions.

Seouli wrote, let’s draw a quadrilateral where length of four sides are 5 cm, 8 cm, 5 cm, and 8 cm respectively, i.e., opposite sides are equal in length.

Let’s see what kind of quadrilaterals are possible using two sticks of length 5 cm and two sticks of length 8 cm.’

Using sticks we see on fixed quadrilateral is possible. So to draw fixed quadrilateral another one condition is required. Now Seouli wrote, let’s draw a fixed quadrilateral whose opposite sides are equal in length and measurement of one angle is 90°. Hence we draw a Rectangle (rectangle square) figure where length is 8 cm and breadth is 5 cm.

Question 11. On another blackboard, Anita drew a rectangle ABCD of which the length is 8 cm and the breadth is 5 cm.
Solution :

each angle of the rectangle ABCD 90° and sum of 4 angles is  360° Measuring by scale, we see

AC = \(\sqrt{89}\)cm and BD = \(\sqrt{89}\)cm, so AC = BD [put=/≠] and AO = OC [put=/≠] BO = QD [put=/≠]. Let’s measure with a protractor, ∠AOD = 90° [put=/≠]

∴ Both the diagonals of rectangular figure ABCD bisect each other but not at right angle.

Question 12. Seoli wrote, I draw a quadrilateral PQRS, of which PQ=5cm QR=8 cm RS=5 cm, PS = 8 cm and ∠PQR = 45°; So PQRS is a parallelogram (parallelogram / rectangular region).

Solution :

Tuhin drew a parallelogram PQRS on another blackboard where PQ = 5 cm, QR = 8 cm, RS = 5 cm, PS = 8 cm, and ZPQR = 45° ∠PQR = 45°, ∠QRS =135°, ∠RSP = 45°, ∠SPQ = 135°

∴ The sum of measurement of 4 angles = 360°. Now measuring by scale we

PR =3.5 cm QS =5.5cm PO = OR [put=/≠] QO = OS [put=/≠]

∴ So both the diagonals bisect each other [ I also draw the diagram in exercise book and verify it measuring by myself].

Question 13. Now Tithi drew a square region of which each side is 4 cm.

Solution :

Each side of square LAND [4] cm measure of each angle 90 and LN and AD diagonals are equal [equal/unequal] LO = I ON [put =/≠ Put], AO = OD [ put=/≠] Measuring with the help of protractor we see ∠LOD = 90°

Both the diagonals of a square region bisect each other.

Question 14. Asif Iqbar drew a Rhombus LION of length of each side 5 cm and ∠LIO = 60°. Let’s measure with protractor.

Solution :

∠LIO = 60°, ∠ON = 120°, ∠ONL = 60°, ∠NLI = 120°, and ∠LXN = 90° The sum of measurement of four angles of the rhombus = 360°

Let’s see by measuring with scale, LX = XO [=/≠] and IX = XN [=/≠].

∴ Both the diagonals of a rhombus bisect each other perpendicularly. Let’s see what I found –

(Parallelogram):

1. Length of opposite sides are equal
2. Measurements of opposite angles are equal
3. Generally length of diagonals are: unequal
4. Diagonals bisect each other

Quadrilateral whose both pairs of opposite sides are parallel with each other.

(Rhombus):

1. Length of all sides are equal
2. Measurements of opposite angles are equal
3. Generally length of diagonals are unequal
4. Diagonals bisect each other at right angles

(Rectangle):

1. Generally length of all sides are equal
2. Generally, measurement of all angles are l 90° I
3. Length of diagonals are equal
4. Diagonals bisect each other

Parallelogram whose one angle is right angle

(Square):

1. Length of all sides are equal
2. Measurement of each angle is 90°
3. Length of diagonals are equal
4. Diagonals bisect each other

Parallelogram whose one angle is a right angle and one pair of adjacent sides are equal in length.

1. With two 45° – 90° sets square, I shall find square [rectangle/ square]
2. With two 30° – 60° – 90° sets square, I shall find [ [rectangle/ square]
3. With two measurement set square, I shall find parallelogram.

Activity

Many of us drew squares of various sizes in our exercise books. After that, we coloured the square shaped paper and cut them.

Question 1. Folding my blue square shaped paper, I made 90°, 45° and 22 \(\frac{1}{2}\)° angles.

Solution :

At first took a square shaped paper

Finding along with diagonal BD and then unfolding it, I got →

Mingling the sides BD and BC with each other then folding and after that unfolding it, I got

Measuring with the protractor I find ∠ABC = 90

Folding my green square shaped paper I try to make 15°, 30° and 60° angles.

At first, I take my green square shaped paper.

“WBBSE Class 8 Algebraic Expression solutions, Chapter 1 worksheet”

Question 2. With the help of scale, pencil and compass, draw 90°, 45°, 22 \(\frac{1}{2}^{\circ}\), 60°, 30°, 120°, 75°, 105°, 135°, 150° angles.

Solution :

Question 3. In quadrilateral PLAN opposite sides are equal in length, i.e., PL = AN = 6 cm and PN = LA = 5 cm. Let’s draw three types of quadrilateral PLAN and let’s see when it will be a rectangle.

Solution:  6cm 4 cm.

∠PLA = ∠LAN = ∠ANP = ∠NPL = 90°

When all angles are 90° then PLAN becomes a rectangle.

Question 4. Let’s write what conditions are required to draw a fixed parallelogram.

Solution:

To draw a parallelogram, at least the length of one side is required.

Question 5. Let’s see what conditions are required to draw a fixed square.

Solution:

To draw a fixed square, at least length of two sides and measure of one angle are required.

Question 6. Let’s draw a square DEAR where DE = 5.6 cm.

Solution:

DEAR is a square where DE = EA = AR = RD = 5.6 cm and each angle is 90°.

Question 7. Let’s draw a rectangle BEST where BE = 6 cm and ES = 4.8 cm.

Solution :

BEST is a rectangle where BE = 6 cm. and ES = 4.8 cm.

Question 8. Let’s draw a rhombus HOME where Z HOM = 60° and HO = 6 cm.

Solution :

HOME is a rhombus whose HO = 6 cm, ∠HOM = 60°,

Question 9. Let’s draw a parallelogram ROAD where RA = 8 cm and OD = 6 cm, 8cm 6 cm

Solution :

ROAD is a rhombus where RA = 8 cm and OD = 6 cm.

Question 10. Let’s draw a parallelogram GOLD where GO = 7 cm, OL = 5.8 cm and GL = 5.8 cm.

Solution:

ROAD is a rhombus where RA = 8 cm and OD = 6 cm.

Solution: 7cm 5.8cm

GOLD is a rhombus where GO = 7 cm, OL = 5.8 cm and GL = 5.8 cm.

Question 11.

1. ABCD is a rectangle. If AC = 5 cm, let’s write the length of BD.

Solution:

The diagonals of a rectangle are equal in length.

∴ ABCD is a rectangle whose length of one diagonal is AC = 5 cm.

∴ BD = 5 cm.

2. PQRS is a square two diagonals PR and QS intersect at O. PR = 5 cm Let’s write the length of QO.

Solution:

The diagonals of a square bisect each other at right angles. Length of one diagonal PR is 5 cm.

∴ Half of one diagonal OQ = \(\frac{5}{2}\) cm. = 2.5 cm.

3. Let’s write the measurement of ∠ABC in parallelogram ABCD where ∠ADC = 60°.

Solution:

Opposite angles of a parallelogram are equal.

∠ABC = ∠ADC = 60°

4. The diagonals AC and BD of rhombus ABCD intersect at O. Let’s write the measurement of ∠AOB.

Solution:

The diagonals of a rhombus bisect each other at right angles.

∴ ∠AOB = 90°

5. A square is always a rhombus but a rhombus is not always a square

6. A square is always a rectangle but a rectangle is not always a square