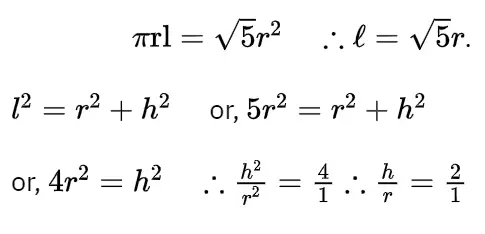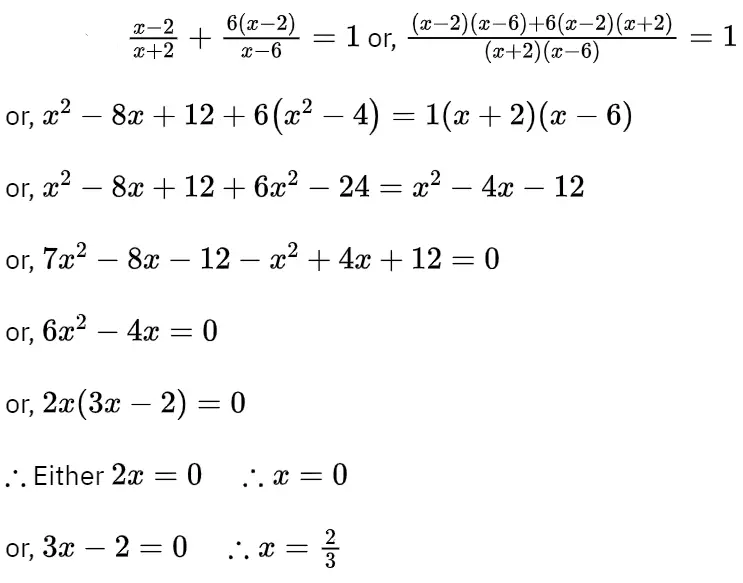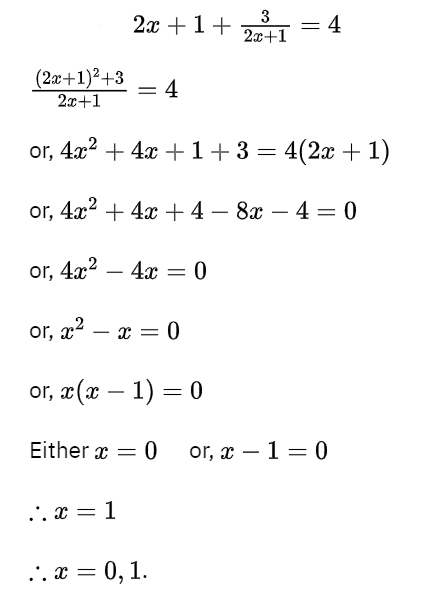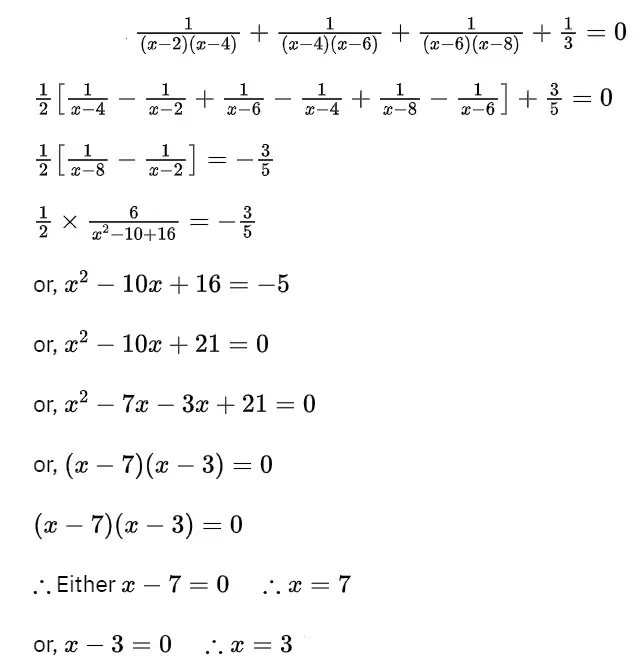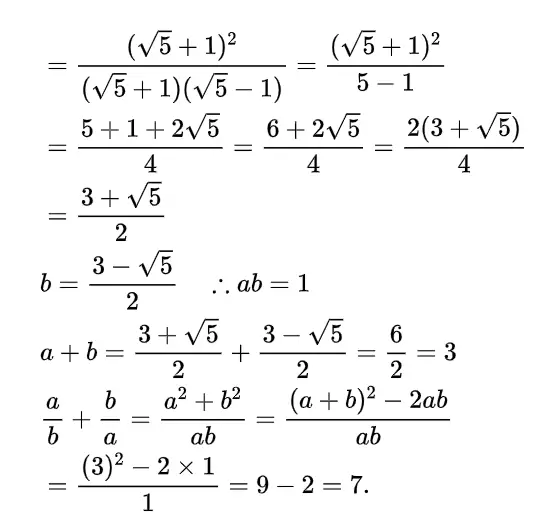Class 10 Maths

Model Question Paper 2023 Mathematics set 3

 

Model Question Paper 2023 Mathematics set 3 MCQs

 

Question 1. Interest on principal amount Rs. b at the rate of simple interest a% per annum for C months is

1. Rs. abc/1200
2. Rs. abc/100
3. Rs. abc/200
4. Rs. abc/120

Solution: l = prh/100

= Rs. abc/12 / 100

= Rs. abc/1200

Answer. 1. Rs. abc/1200

Question 2. The ratio of the capital amounts in a joint business invested by Tirtha, Bulu, and Rabeya is 10:12: 15 if the profit at the end of the year is Rs. 7,400. Rabeya will get a share of the profit of

1. Rs. 2,000
2. Rs. 2,400
3. Rs. 3,000
4. Rs. 2,800

Solution: 

The ratio of the capital amounts in a joint business invested by Tirtha, Bulu, and Rabeya is 10:12: 15 if the profit at the end of the year is Rs. 7,400.

Share of profit of Rabeya = 15/10+12+15

= 15/37 x Rs. 7,400

= 15/37 x Rs. 7,400 

= Rs. 3,000

Answer. 3. Rs. 3,000

Question 3. If x ∝ y, then

1. x² ∝ y²
2. x³∝ y²
3. x∝ y3
4. x²∝ y²

Answer. 4. x² ∝ y²

Question 4. If the roots of quadratic equation kx²-5x+ k = 0 are real and equal, the value of k is

1. ± 5
2. ± 5/2
3. ± 2/5
4. ± 2

Solution: When roots are equal, discriminant = 0

i.e., (-5)²-4 K       K = 0

∴ K²= 25/4

∴ K = ± 5/2

The value of k is ± 5/2

Answer: 2. ± 5/2

Question 5. If a/3 = b/4 = c/7 = 2a-3b+c / x

1. 1
2. 2
3. 3
4. 4

Solution: x = 2 x 3 – 3 x 4 +7

= 6-12+7

= 1

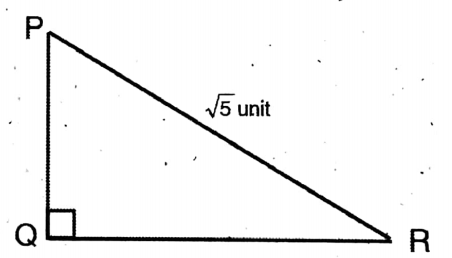
Question 6. If x = √7 + √6, the value of x + 1/x is 

1. 2√6
2. √6
3. 2√7
4. √7

Solution: x = √7+√6

∴ 1/x = 1/√7+√6

= √7-√6

=2√7

Answer: 3. 2√7

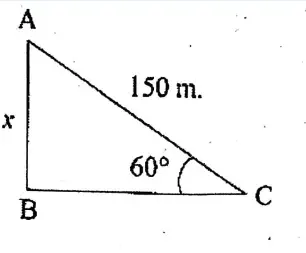
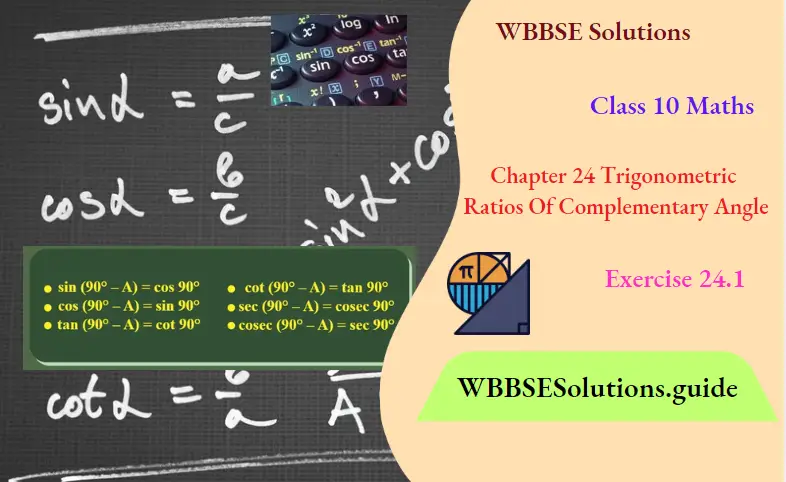
Question 7. If α = 90°, B = 30°, the value of sin(α-B) is

1. 1
2. 1/2
3. √3/2
4. 1/√2

Solution: sin(α-B)=sin(90° – 30°) = sin60° = √3/2

Ans. 3. √3/2

Question 8. The angle measured 1 radian will be

1. acute angle
2. right angle
3. obtuse angle
4. straight angle

Answer. 1. acute angle

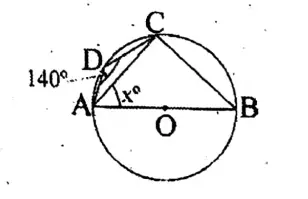
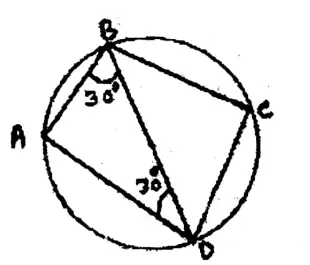
Question 9. In a cyclic quadrilateral ABCD if AB = AD and ∠ABD = 30°, the value of ∠BCD is

1. 90°
2. 30°.
3. 45°
4. 60°

Solution: ∠ADB = ∠ABD = 30°

∴ ∠BAD = 180° -2 (30°)

= 120°

∴ ∠BCD = 180° – 120° 

= 60°

Answer. 4. 60°

 

 

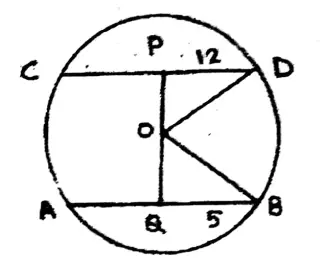
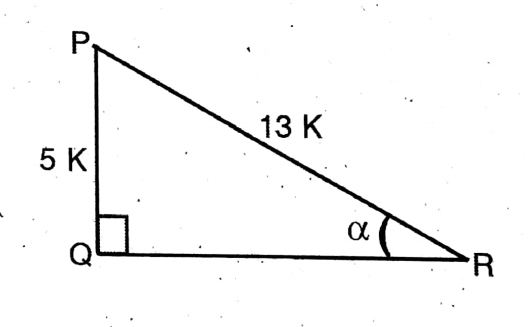
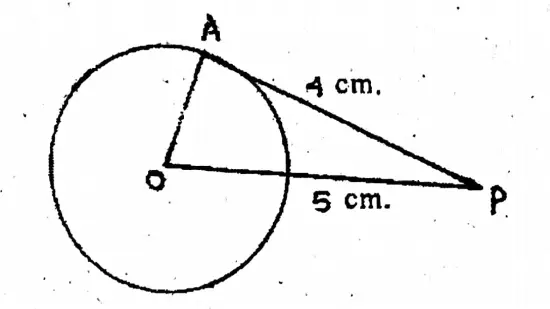
Question 10. The tangent PA is drawn to a circle with center O from the external point P. If PA = 4 cm OP = 5 cm. the radius of the circle is

1. 5 cm.
2. 4 cm.
3. 6 cm.
4. 8 cm.

Solution: OP² = OA² + AP²

The tangent PA is drawn to a circle with center O from the external point P. If PA = 4 cm OP = 5 cm

OA² = OP² – AP²

= 5²-4²=9

∴ OA = √9 = 3

∴ Diameter = 23cm = 6cm.

Answer. 3. 6 cm.

 

 

Question 11 If = AB/DE = BC/FD = AC/EF of ΔABC and ΔDEF,

1. ∠B = ∠E
2. ∠A = <D
3. ∠B = <D
4. ∠A = <F

Answer. 3. <B = <D

Question 12. If the ratio of volumes of two cubes is 8: 125, the ratio of total surface areas of the two cubes will be

1. 2:5
2. 4:25
3. 4:5
4. 2:25

Solution: Ratio of volumes of two cubes = 8: 125

∴ Ratio of sides =3√8/125

= 2/5

Ratio of surface areas = (2/5)²

= 4:25

Answer. 2. 4: 25

Question 13. If the length of the radius of the base of a right circular cone remains the same, the height becomes half of the previous one, then the volume of the cone will be decreased by

1. 25%
2. 50%
3. 75%
4. 100%

Answer. 2. 50%

Question 14. The mode of 1, 3, 2, 8, 10, 8, 3, 2, 8, 8 is

1. 2
2. 3
3. 8
4. 10

Solution: By arranging 1, 2, 2, 3, 3, 8, 8, 8, 8, 10

Answer. 3. 8

Question 15 The median of 8, 15, 10, 11, 7, 9, 11, 13, and 16 is

1. 15
2. 10
3. 11.5
4. 11

Solution: By arranging: 7, 8, 9, 10, 11, 11, 13, 15, 16

n = 9, Median = 9+1/2

= 5th term = 11

Answer. 4. 11

Question 2.

1. If a sum of money at 5% compound interest per annum for 2 years becomes Rs. 615, find the principal amount.

Solution:

If a sum of money at 5% compound interest per annum for 2 years becomes Rs. 615

A = P (1+r/100)ⁿ

∴ C.I = A-P = P (1+r/100)ⁿ – P

= P x 2.05 x 0.05

= 615

P = 615/2.05 x 0.05

= 6000

2. x and y are two variables. Corresponding values related to them are: x=7, y = 9; x = 4, y = 6; x = 12, y = 18; x = 3.6, y = 5.4. Determine the relationship of variation between x and y with reasons.

Solution:

x and y are two variables. Corresponding values related to them are: x=7, y = 9; x = 4, y = 6; x = 12, y = 18; x = 3.6, y = 5.4.

1st case x/y = 112/18 = 2/3

= x/y constant

∴ x α y

3. If the two roots of the quadratic equation x² + 8x + 2 = 0 are α and ẞ, find the value of (1/α + 1/β)

Solution: Here, α+β=-8 & α ẞ=2

1/α 1/β = α+β/αβ

= -8/2

= -4

4. A cylinder and a sphere are of equal radii, and their volumes are also equal. Find out the ratio of the diameter and height of the cylinder.

Solution: Volume of cylinder = 4r³h

Volume of sphere = 4/3 лr³

∴ 3h 4r or, 3h = 2 x 2r.

∴ 2r/h = 3/2

∴ Ratio of diameters: height = 3:2.

5. If the volume of a solid hemisphere is 144л, what is its diameter?

Solution : 2/3лr³ = 144π

r³ = 144 x 3 / 2

= 216

∴ r = 3√216 = 6.

Diameter = 2 x 6 cm = 12 cm.

True Or False

1. Only one circle can be drawn through three non-collinear points.

Answer: True

2. A concyclic parallelogram is a rectangular figure.

Answer: False

Fill In The Blanks

1. The angle in the segment of a circle that is greater than a semi-circle is A cute angle.

2. Perpendicular bisector of any chord passes through the Centre of the circle.

8. If tan2θ = 1, find the value of cos2θ.

tanθ = 1/tan2θ = cot2θ tan(90-2θ)

∴ θ=90-2θ      or, 3θ = 90°        ∴ θ = 30°

∴ cos2θ = cos60° = 1/2

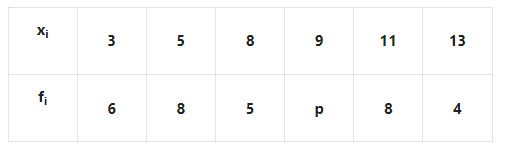
9. The length of the radius of a circle is 14 cm. Find the circular measures of the angle at the center by an arc of this circle 66 cm in length.

Solution: Radian = arc/radian

= 66/15 radius

= 4.71 radians.

 

10.

 

Solution:

 

 

 

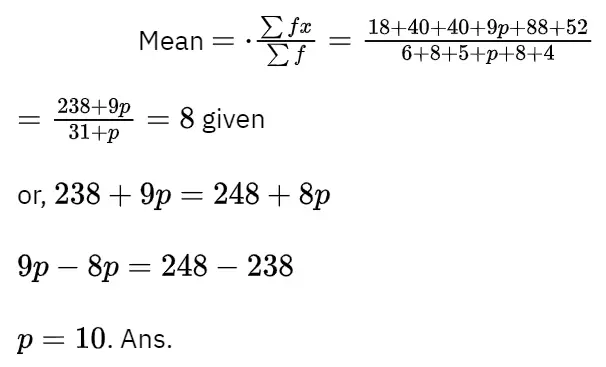
Question 3. At what rate of interest will Rs. 60,000 amount to Rs. 69,984 for 2 years?

Solution: 

 

 

Or, At the start of the year, Arun and Ajoy started a business jointly with a capital of Rs. 24,000 and Rs. 30,000 respectively. After some months Arup Invested Rs. 12,000 more in that business. If the profit after the end of the year was Rs. 14030 and Arun got a profit share of Rs. 7130, determine after how many months Arun Invested the amount.

Solution:

At the start of the year, Arun and Ajoy started a business jointly with a capital of Rs. 24,000 and Rs. 30,000 respectively. After some months Arup Invested Rs. 12,000 more in that business. If the profit after the end of the year was Rs. 14030 and Arun got a profit share of Rs. 7130

Let Arun invest Rs. 12,000 more after x months.

Arun’s Capital throughout the year

= Rs. [24000 × 12+12000 x (12-x)]

= Rs. (288000 + 144000 12000x) 

= Rs. (432000 – 12000x) 

ajoy’s Capital throughout the year

= Rs. 30000 x 12 = Rs. 360000

The ratio of Arun’s Capital & ajoy’s Capital

= (432000-12000x): 360000

= 1000(432-12x): 360000

= (432 – 12x): 360 12(36-x): 360 (36 – x): 30

Total profit= Rs. 14030.

∴Arun’s share of profit = 36-x / (36-x)+30 x Rs. 14030.

= 36-x /66-x x Rs. 14030.

∴According to the given problem,

= 14030 x 36-x/66-x = 7130

or, 36-x/66-x  = 7130/14030

= 713/1403

or, 713(66 – x)= 1403(36 – x)

or, 47058 – 713x= 50508 – 1403x

or, 1403x-713x= 50508-47058 

or, 690x = 3450

∴x = 3450/690

= 5

∴ After 5 months Arun invested Rs. 12,000 more.

 

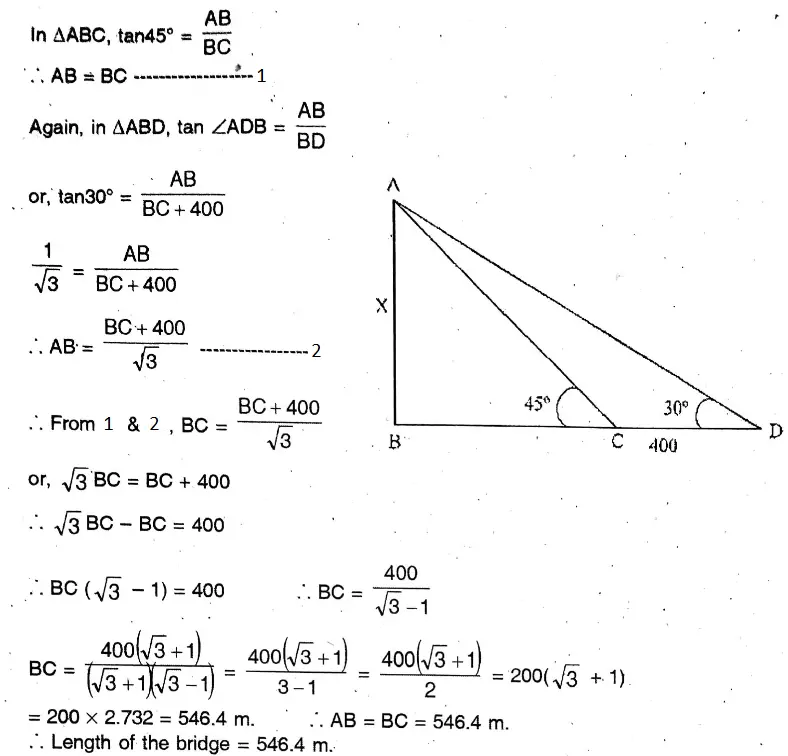
Question 4. Solve : 1/a+b+x = 1/a + 1/b + 1/x , [x = 0, – (a + b)]

Solution:

 

 

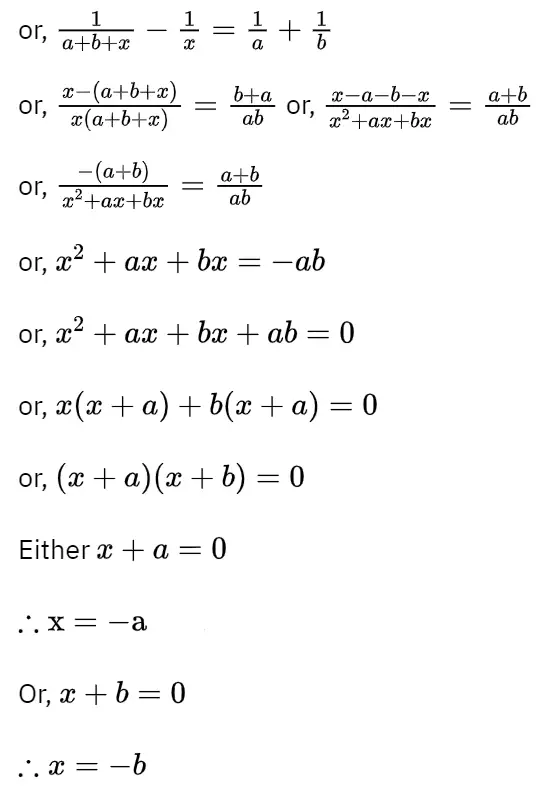
Or, The velocity of a boat is 8 km/h in the still water. The boat takes 5 hours to cover 15 km downstream and 6 km upstream. Find the velocity of the current. 

Solution: Let the speed of current = x km/hr.

As the speed of the boat = is 8 km/hr.

∴ Speed of the boat with the current = (8 + x) km/hr. 

& Speed of the boat against the current = (8x) km/hr. 

∴ According to the problem,

15/8+x + 22/8-x

or, 15(8-x)+22 (8+x)/(8+x) (8-x) = 5

or, 120-15x+176 + 22x=5 (64 – x²)

or, 296 +7x=320-5x²

or, 5x²+7x-24=0

or, 5x² + 15x- 8x-24 = 0

or, 5x (x+3)-8 (x+3)=0 or, (x+3) (5x-8)= 0 

Either x+3=0                           ∴ x = – 3 (Not possible)

Or, 5x-8=0                              ∴ 5x = 8

∴ X = 8/5

= 1 3/5 km/hr. 

Question 5. √5/√3+√2 – 3√3/√2+√5 + 2√2/√3+√5

Solution:  Given =  √5/√3+√2 – 3√3/√2+√5 + 2√2/√3+√5 ———–(1)

 

 

 

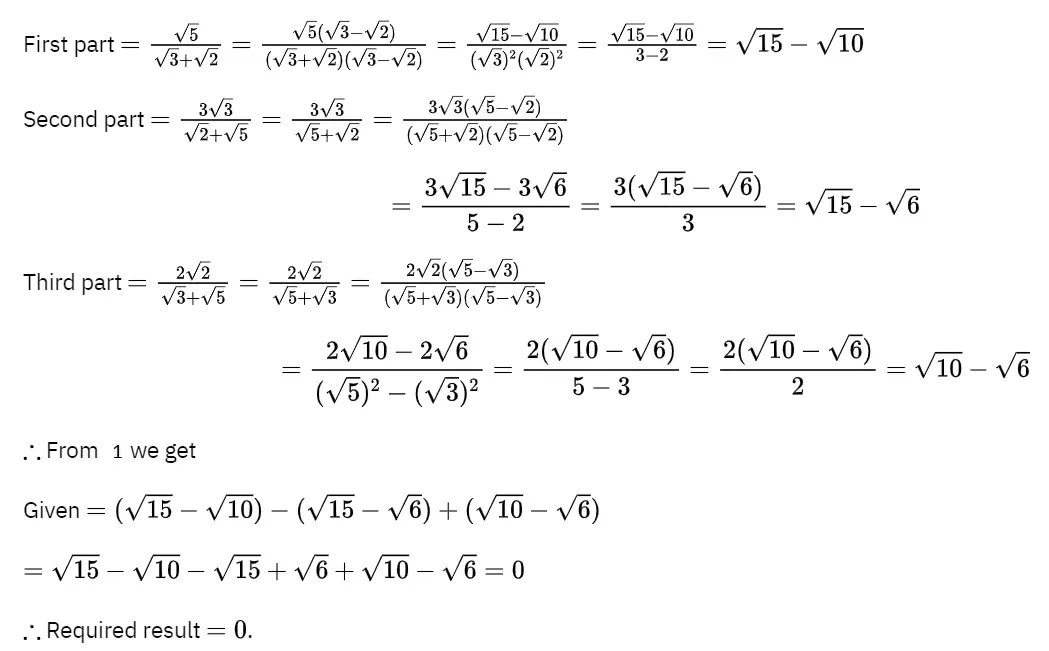
Or, If 5 men can harvest jute cultivated in 10 bighas of land in 12 days, how many farmers can harvest jute cultivated in 18 bighas in 9 days? Determine this by applying the variation theorem.

Solution: Let the number of farmers be A,

number of days be B and area of land be C

The number of farmers is in direct variation with the area, of land, when the number of days remains constant.

∴ A ∝ C, when B is constant.

Again, if the area of land remains constant, then the number of farmers is in inverse variation

with the number of days, i.e., Aα 1/B

when C is constant.

∴  According to the theorem on joint variation, A α C/B, when B and C both vary.

i.e., A = K C/B [where, K is non zero constant] ———–(1)

Given A= 5, B = 12 and C = 10

From (1) we get 5 K = 10/12

or, K = 5×12/10          ∴ K = 6

Now, putting the value of K in equation (1) we get A = 6 C/B ——–(2)

If B = 9 and C = 18 then, we get from (2), A =  6 x 18/9

= 12

∴ Required number of farmers = 12.

Question 6. If ay – bx / c = cx – az / b = bz – cy/a, proved that x/a = y/b = z/c.

Solution: ay – bx / c = cx – az / b = bz – cy/a

∴ c(ay – bx) + b(cx – az) + a(bz – cy) / c²+b²+a²

= cay -cbx + bcx – baz +abz – acy / c²+b²+a²

= 0    [using addendo we get]

so, ay – by / c = 0     or, ay – bx = 0

or, ay = by        ∴ y/b = x/a

Again, cx – az / b = 0        or, cx = az            ∴ x/a = z/c

∴ x/a = y/b = z/c [proved]

 

Or, If a,b, and c are in continued proportion, prove that a²b²c²(1/a³ + 1/b³ + 1/c³) = a³+b³+c³

Solution: To prove, a²b²c²(1/a³ + 1/b³ + 1/c³) = a³+b³+c³

 

 

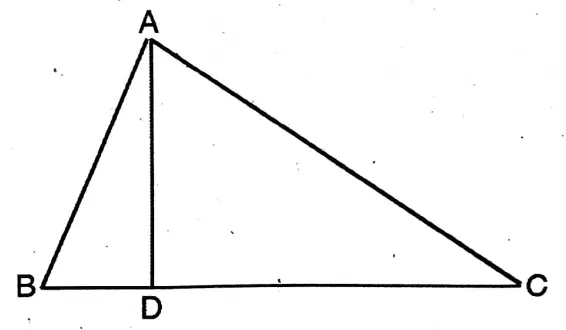
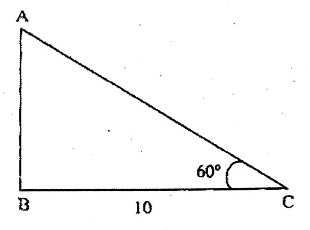
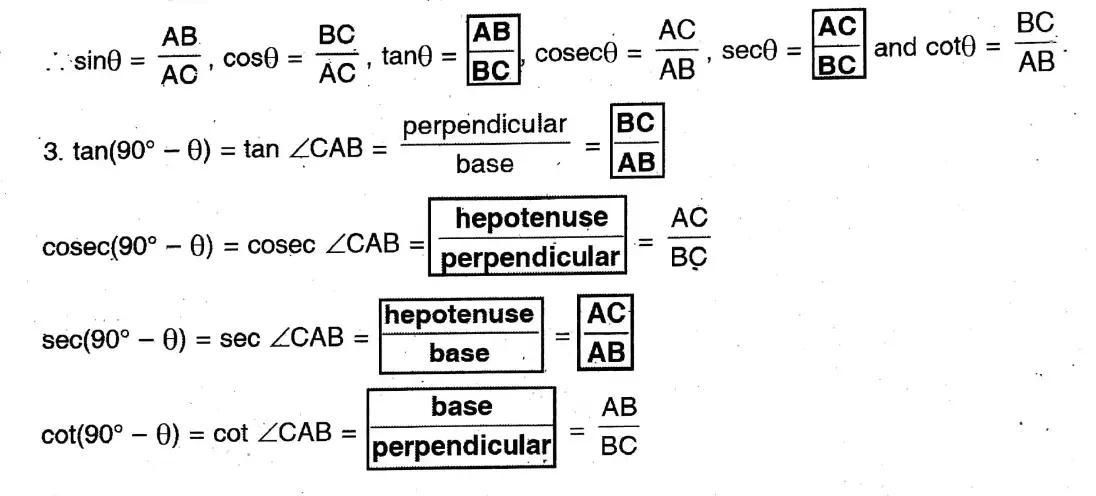
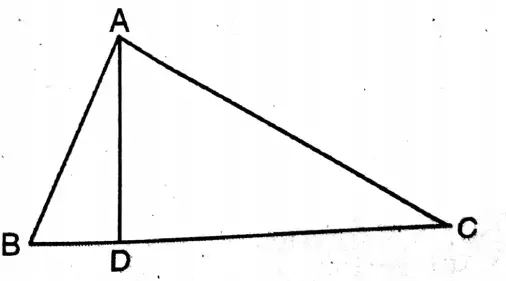
Question 7. State and prove Pythagoras’ theorem.

Solution:

Given: ABC is a right-angled triangle whose∠A is a right angle.

To prove: BC²= AB² + AC²

Construction: I draw a perpendicular AD on the

hypotenuse BC from the right angular point A which intersects the side BC at point D.

Proof: In right-angled triangle ABC, AD is perpendicular on the hypotenuse BC

∴ ΔABD and ΔCBA are similar.

Hence AB/BC = BD/AB,        ∴ AB² = BC.BD———-(1)

Again, ΔCAD and AGBA are similar.

Hence, AC/BC = DC/AC,       ∴ AC² = BC.DC

So, by adding (1) and (2), I get, AB²+ AC² = BC.BD + BC.DC

= BC(BD+ DC) = BC.BC= BC²

∴ BC² = AB²+ AC² Proved.

 

Or, Prove that the opposite angles of a cyclic quadrilateral are supplementary. 

Solution:

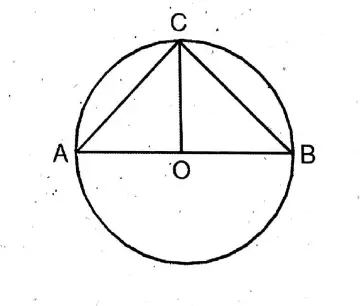
Given: ABCD is a cyclic quadrilateral of a circle with center O.

To prove that: ∠ABC + ∠ADC= 2 right angles and <BAD +∠BCD 2 right angles

Construction: A, O, and C, O are joined.

Proof: ∠AOC is the reflex angle at the center and ABC is the angle at the circle arc formed with the circular area ADC.

∴ Reflex∠AOC = 2∠ABC

∴ ∠ABC = 1/2 reflex ∠AOC———(1)

Again, ∠AOC is the angle at the center and ZADC is the angle at the circle formed with the circular area ABC.

∴ ∠AOC = 2∠ADC

∴ ∠ADC = 1/2 ∠AOC———(2)

∴ From (1) and (2), we get∠ABC + ∠ADC 

= 1/2(reflex ∠AOC+ ∠AOC)

= 1/2 x 4 right angles = 2 right angles

 

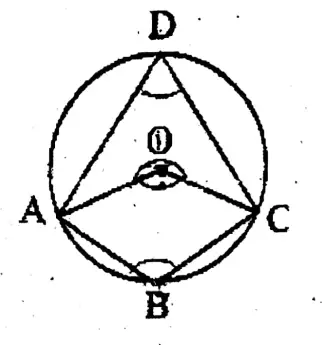
Similarly by joining B, O and D, O; it can be prove that /BAD + BCD = 2 right angles (Proved)

Alternative proof:

Given: ABCD is a cyclic quadrilateral.

To prove that: ∠ABC + ∠ADC= 2 right angles and ∠BAD + ∠BCD 2 right angles

Construction: Two diagonals AC and BD are drawn.

Proof: ∠ADB = ∠ACB [angle in the same segment of the circle] Again, BAC = BDC [angle in the same segment of the circle]

Again, ∠ADC = ∠ADB + ∠BDC=∠ACB + <BAC

∴ ∠ADC + ∠ABC = ∠ACB + ∠BAC + ∠ABC

∴ ∠ADC + ∠ABC= 2 right angles [sumof there angles of a triangle is 180°]

Similarly, we can prove that ∠BAD + ∠BCD = 2 right angles. Proved.

 

 

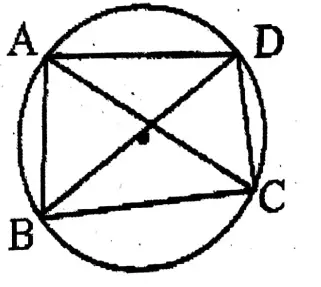
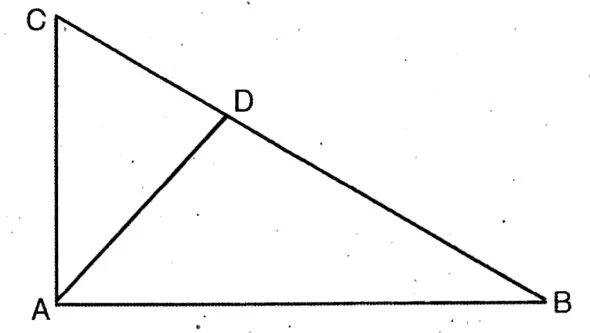
Question 8. ABCD is a trapezium of which AB || DC; a straight line parallel to AB intersects AD and BC at the points E and F respectively. Prove that AE: ED = BE: FC. 

Solution:

Given: AB | DC in the trapezium ABCD; the straight line parallel to AB has intersected AD and BC at the points E and F respectively.

To prove: AE: ED = BF: FC.

Construction: I joined A, C which has intersected EF at the point G.

Proof: In ΔADC, DC || EF

So, from Thales theorem, we get, AE/ED

= AG/GC ———(1)

Again, in ΔACB, AB || FG

∴ From Thales theorem, we get, AG/GC

= BF/FC ———(2)

So, from (1) and (2), we get AE/ED = BF/FC

∴ AE ED = BF: FC

 

 

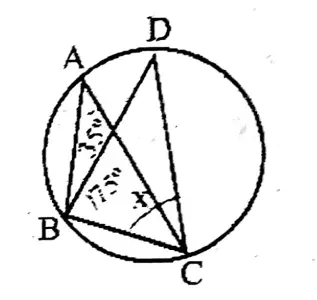
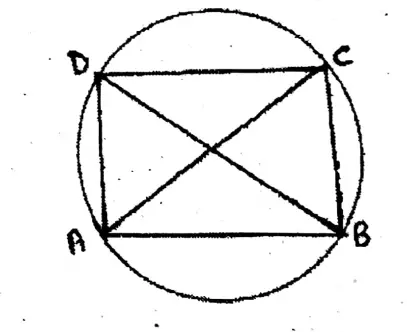
Or, In a cyclic quadrilateral ABCD if AB = DC, prove that AC = BD.

Solution: ABCD is a cyclic quadrilateral.

∴ AB = DC

To prove AC BD

In ΔABC & ABCD,

(1) AB = CD, BC is common

∠DBC = ∠BAC (angle on same arc)

∴ ΔABC ≅ ΔBCD

∴ AC = BD.

 

 

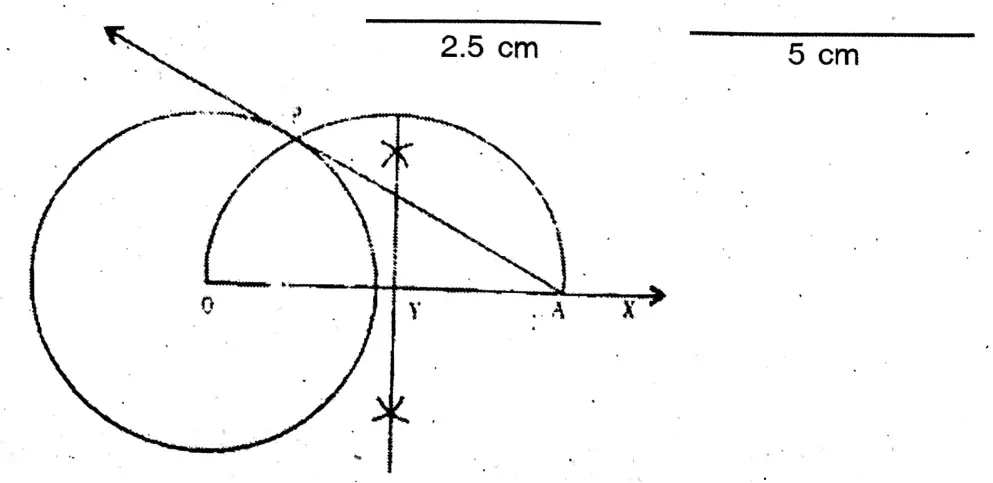
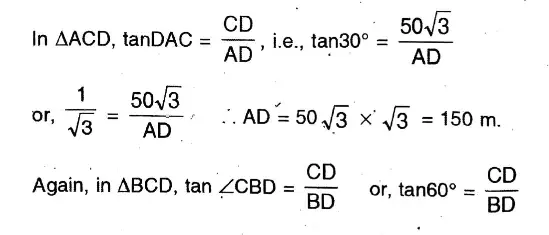
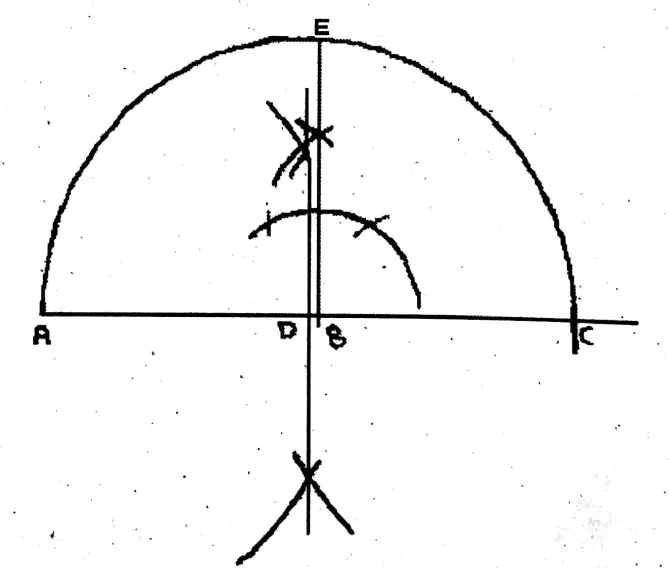
Question 9. Find the value of √22 geometrically. 

Solution: 22=5 x 4.4

From AX, cut AB = 5 cm & BC = 4.4 cm. 

O is the midpoint of AC.

Draw a semicircle with center O.

Now draw a perpendicular at B on AC, which cuts the semicircle at D.

Length of BD is the value of √22 = 4.7 (approx)

 

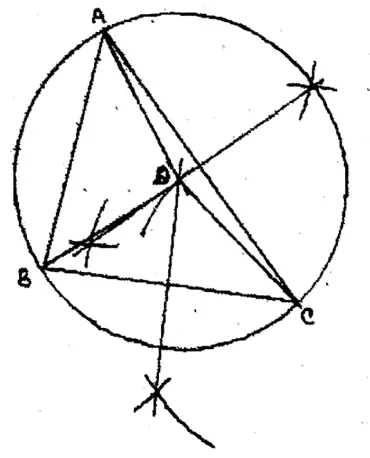
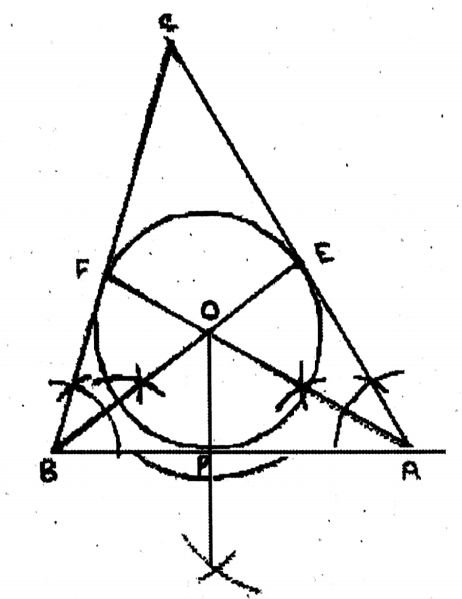
Or, Draw a triangle having a side of 6.5 cm in length and measures of two angles adjacent to the side are 50° and 75°. Draw the in-circle of that triangle.

Solution: ABC is an A whose

C = 75° & B = 50°, BC = 6.5 cm.

O is the center of the incircle.

 

 

Question 10. Answer any two questions :

1. Find the value of x from the equation (x + 1) cot² Π/6= 2cos²Π/3 +3/4 sec²Π/4 +4sin²Π/6

Solution: (x + 1) cot² Π/6= 2cos²Π/3 +3/4 sec²Π/4 +4sin²Π/6

 

 

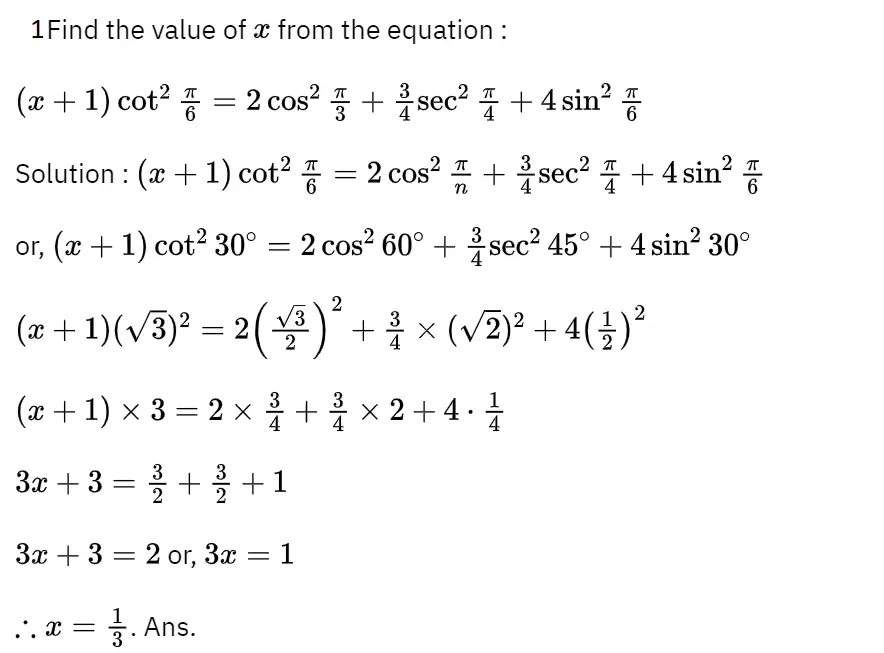
2. Show that cosec²22° cot 68° = sin² 22° + sin²68° + cot²68°. 

Solution: L.H.S. = cosec²22°. cot²68°

=cosec²(90° – 68°) cot²68°

= sec²68°. cot²68°

= 1/cos² 68° x cos² 68° / sin² 68°

= 1/sin² 68°

= cosec²68°

R.H.S= sin²22° + sin²68° + cot²68° 

= sin²(90° – 68°) + sin²68° + cot²68°

= cos²68° + sin²68° + cot²68°

= 1 + cot²68°

=cosec²68°

∴ L.H.S. =  R.H.S.

3. If cose = X/√x²+ y², show that x sine = y cose.

Solution: sinθ = √1-cos²0 =√1 – (x/√x²+y²)²

 

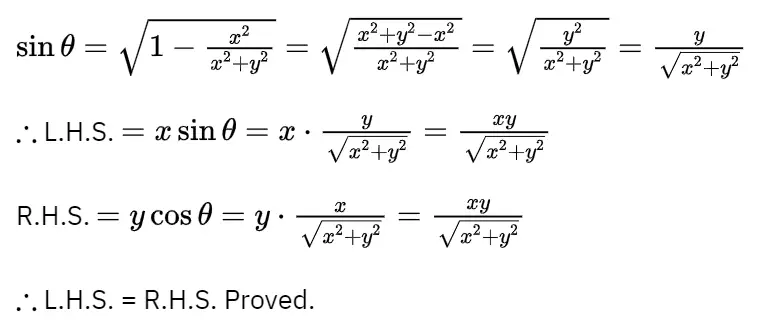
Question 11.

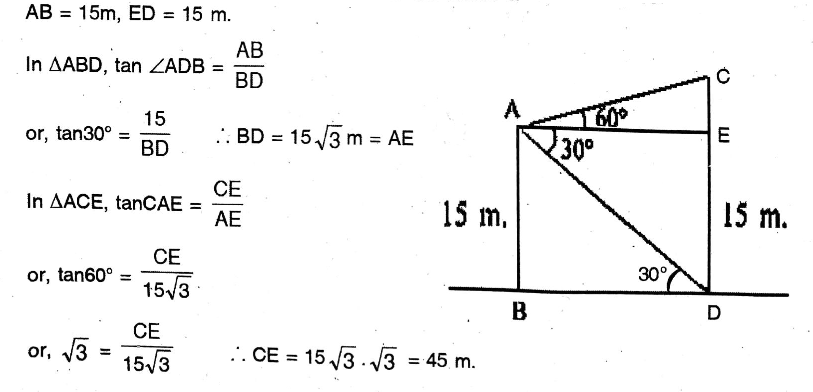
1. A hemisphere and a cone have an equal base and their heights are also equal, find the ratio of their volumes and the ratio of their curved surface areas.

Solution: Height of hemisphere = Radius of base = r

Height of cone Radius of base = r

 

 

 

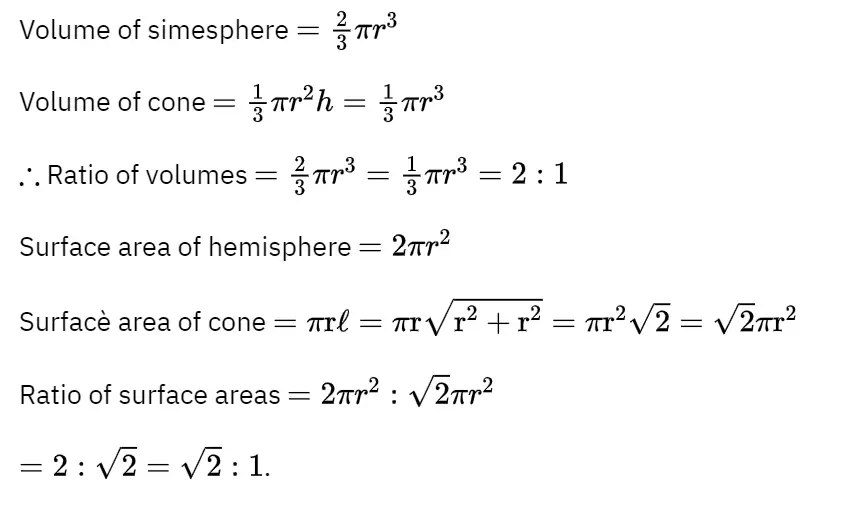
2. Find the volume of a right circular cone obtained from a wooden cube of 4.2 dcm edge by wasting minimum quantity of wood.

Solution: Here diameter of base of the cone one edge of cube.

Radius = 4.2 / 2

= 2.1 dcm 

= 21 cm

Height of cone one edge of cube = 42 cm..

Volume= 1/3г²h= X

= 1/3 x 22/7 x 21 x 21 x 42 cu cm.

= 22 x 21 x 42 cu cm 

= 19404 cu cm.

∴ Volume of cone = 19404 cu cm. Ans.

 

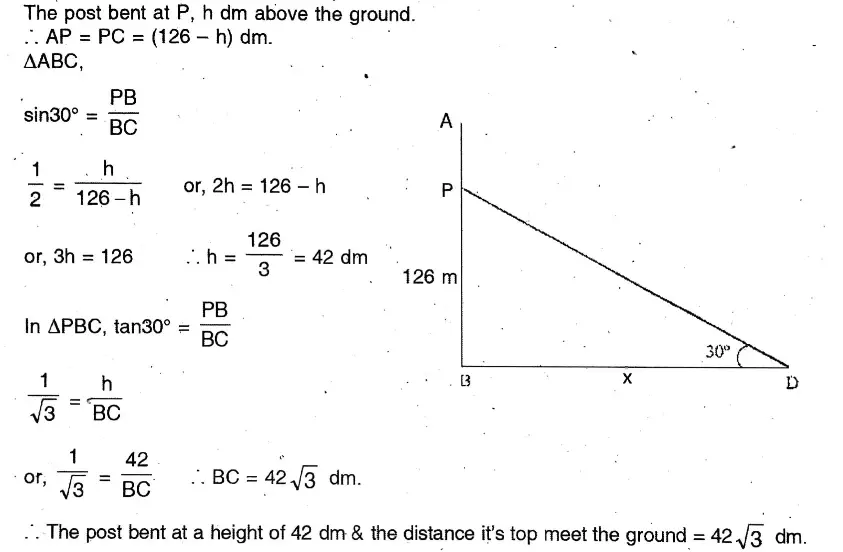
3. Height of a right circular cylinder is twice of its radius. If the height would be 6 times of its radius, then the volume of the cylinder would be greater by 539 cubic dm. Find the the height of the cylinder.

Solution:

Height of a right circular cylinder is twice of its radius. If the height would be 6 times of its radius, then the volume of the cylinder would be greater by 539 cubic dm.

Let the height of the cylinder = h dcm & radius = r dcm.

∴ h = 2r

Volume of the cylinder = r² x 2r= 2πr³

If height h = 6r, volume = r² x 6r = 6πr³

According to the problem, 6r³-2r³ = 539

4πr³ = 539

or, 4 x 22/7 r3 = 539

∴ r³ = 539 x 7 / 88

= (7/2)³

∴ r= 7/2

∴ 2r= 7.

∴ Height = 2r = 7dcm.

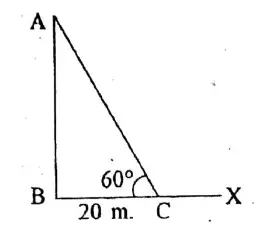
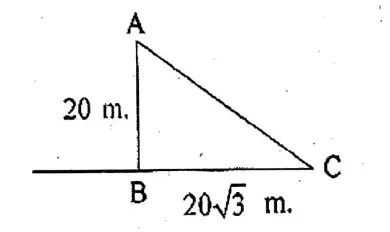
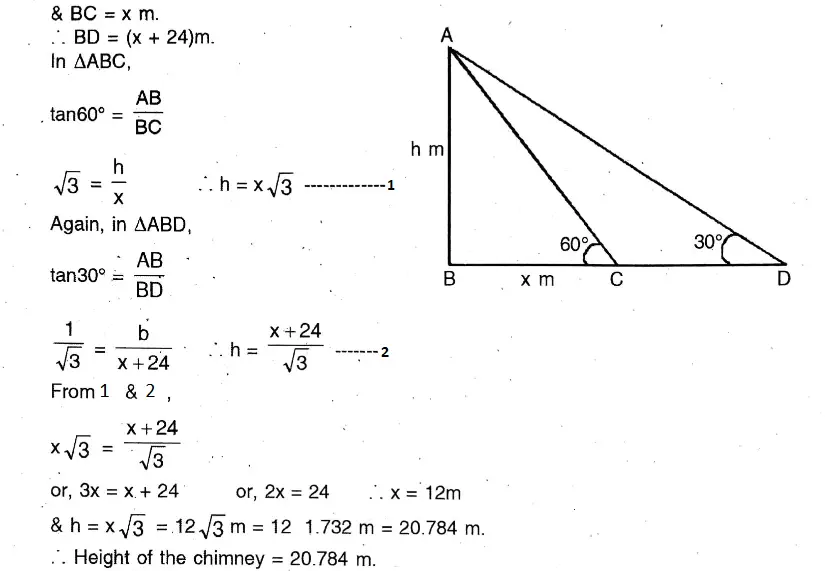
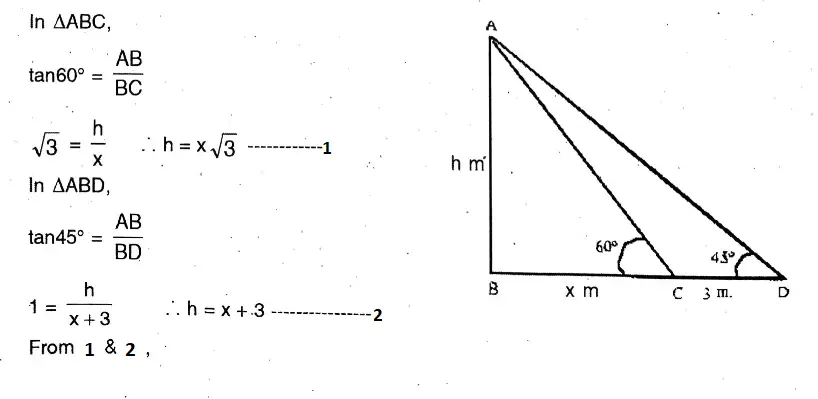
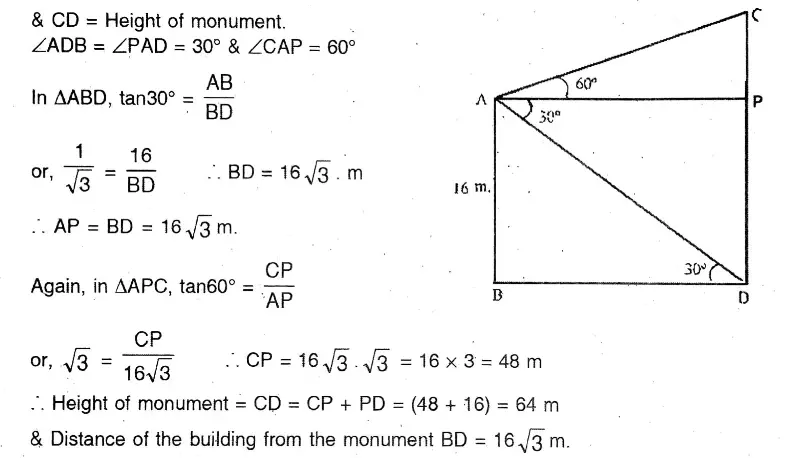
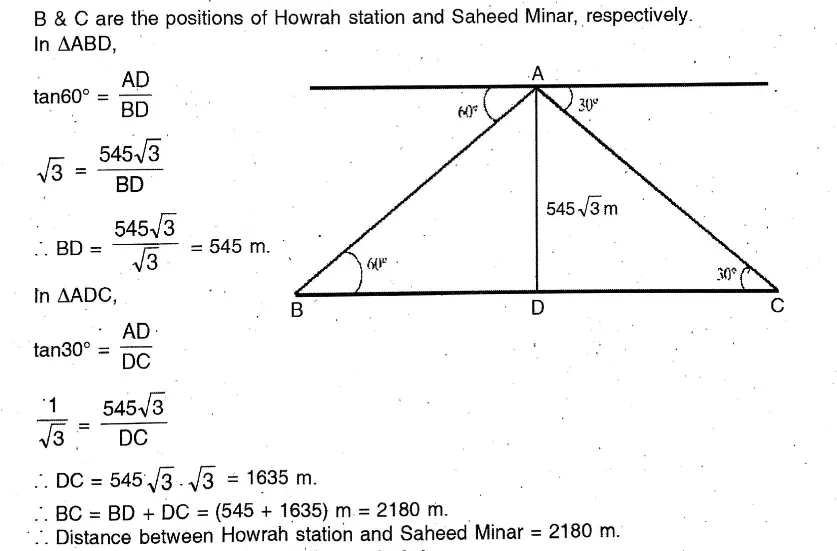
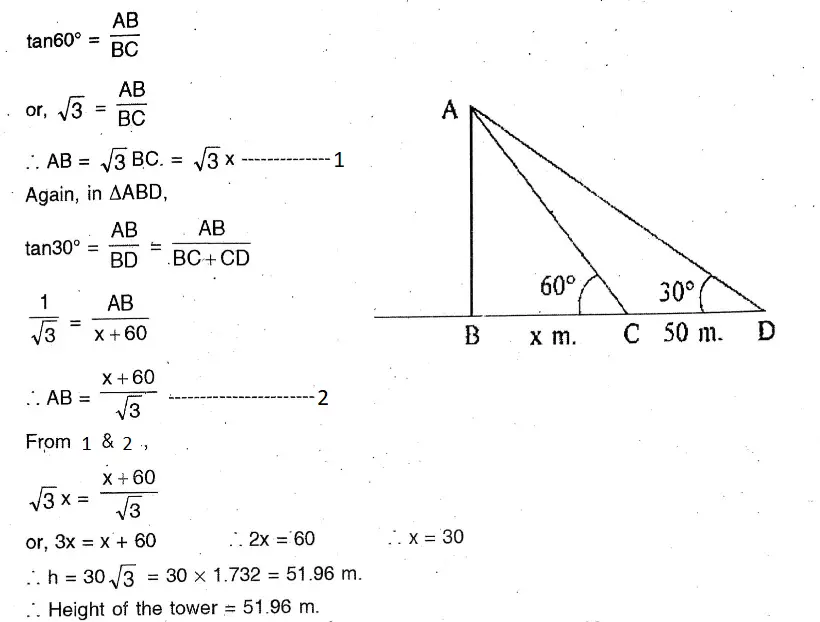
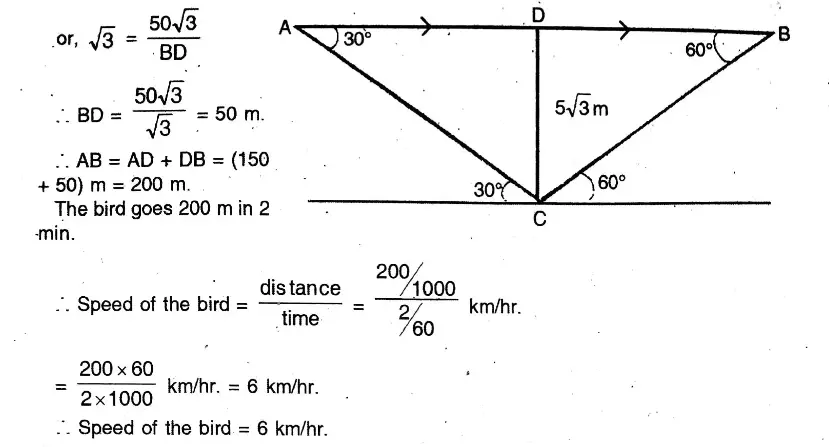
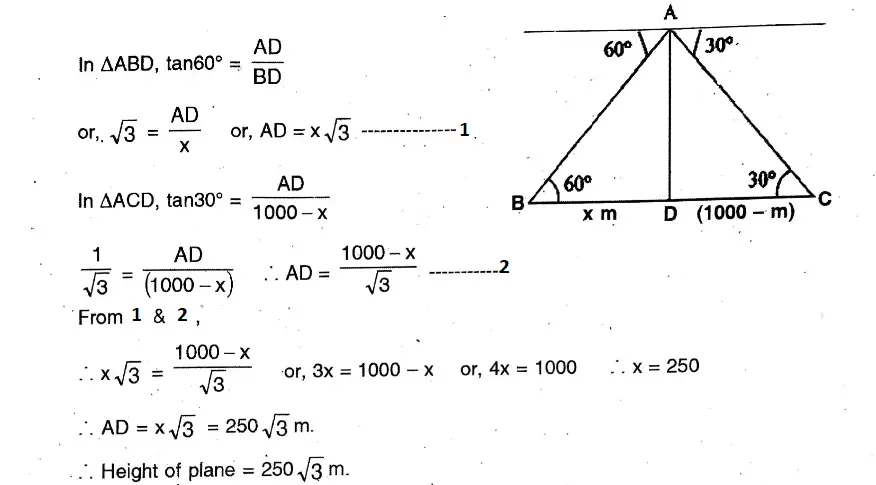
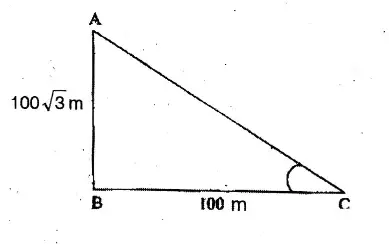
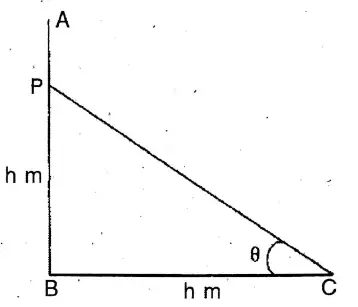
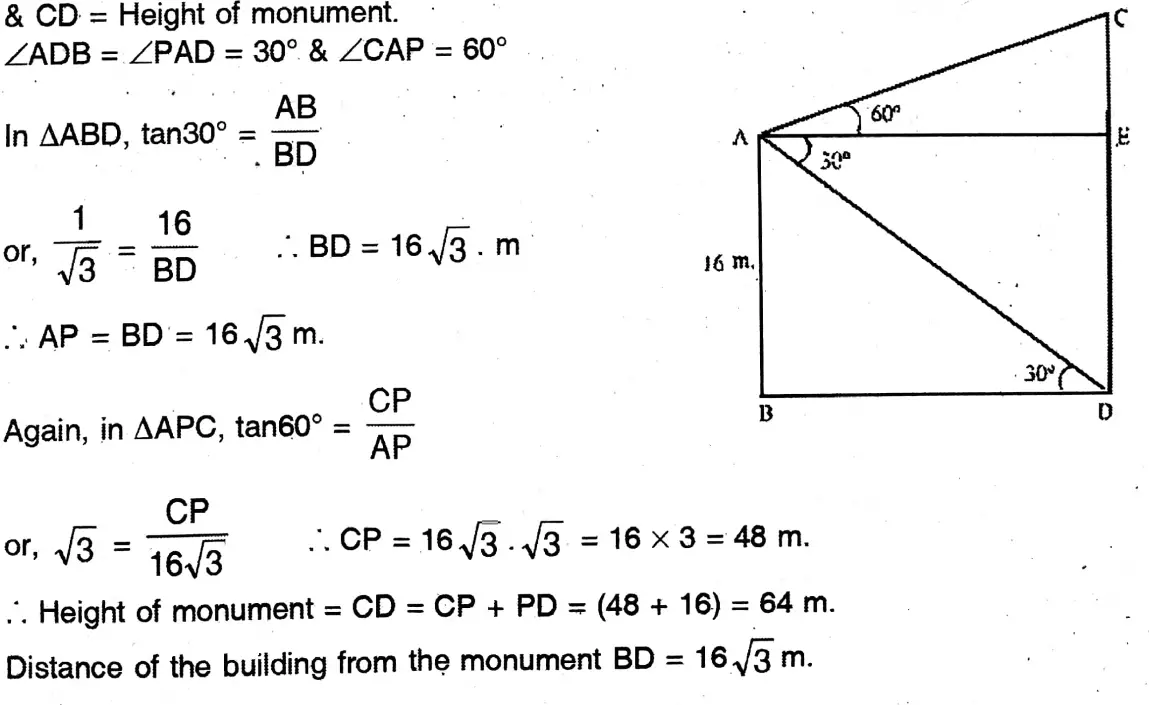
Question 12. The angle of elevation and the angles of depression of the top and foot of the monument, when observed from a point on the roof of a five-storied building of Mihir, are 60° and 30° respectively. If the height of the building is 16 metre, what will be the height of the monument ?

Solution:

The angle of elevation and the angles of depression of the top and foot of the monument, when observed from a point on the roof of a five-storied building of Mihir, are 60° and 30° respectively.

Let AB 16 m Height of the building

 

 

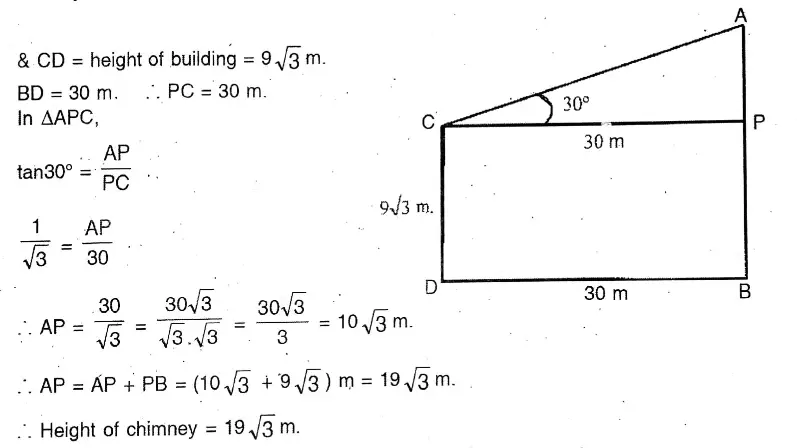
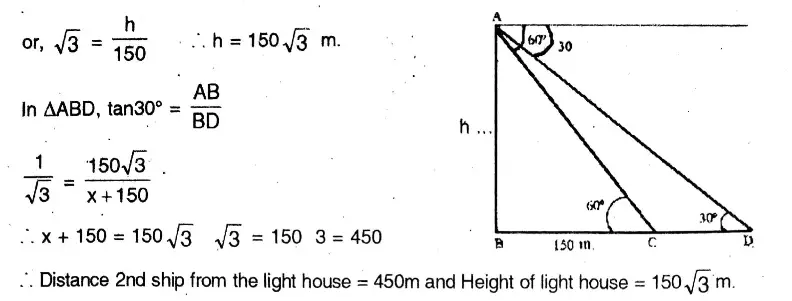
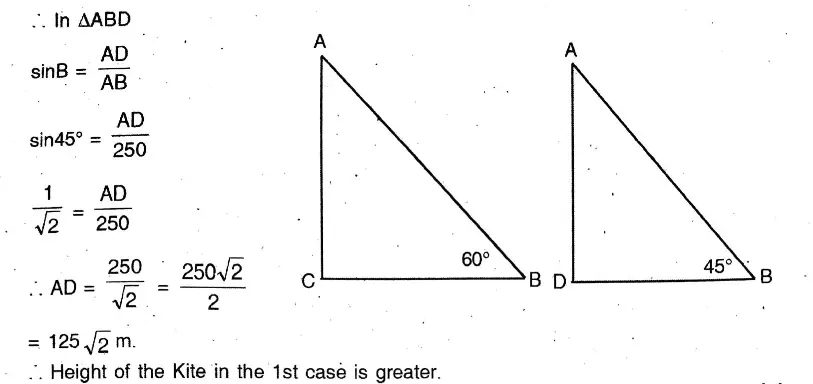
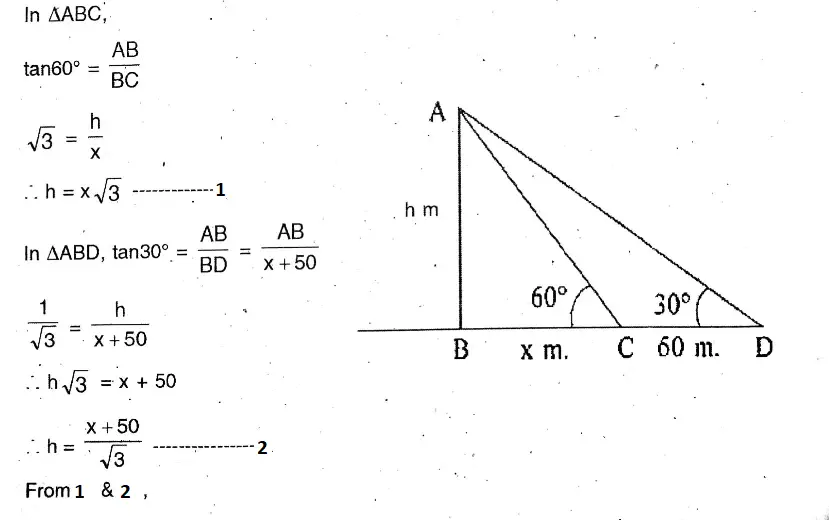
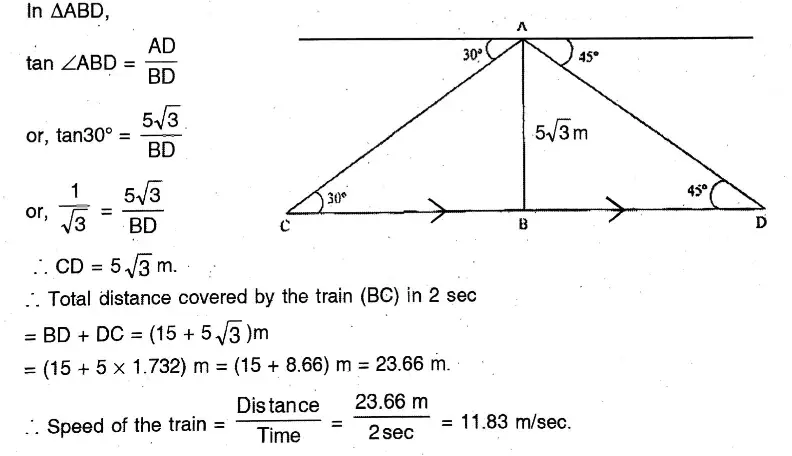
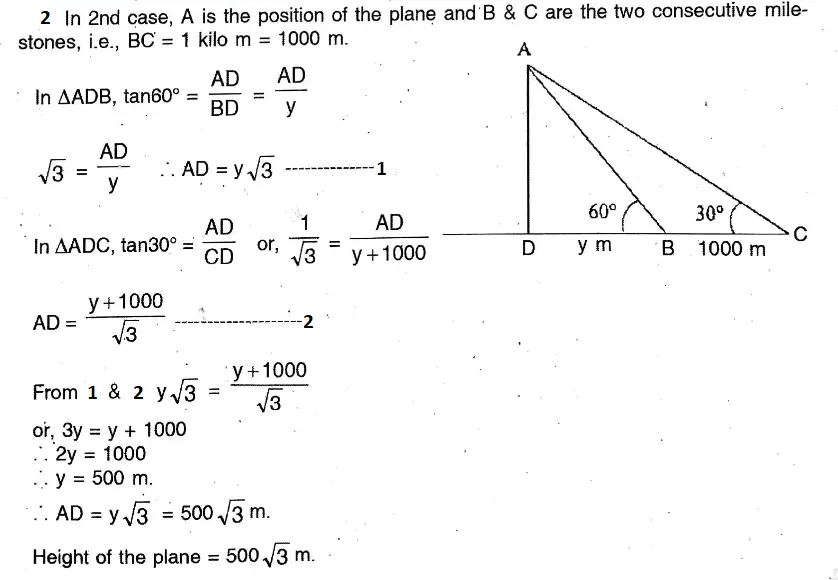
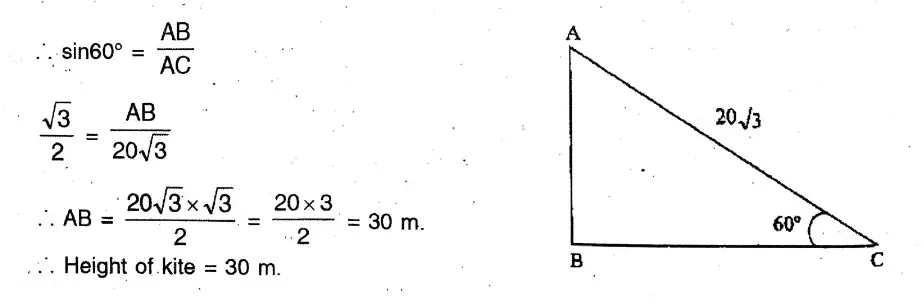
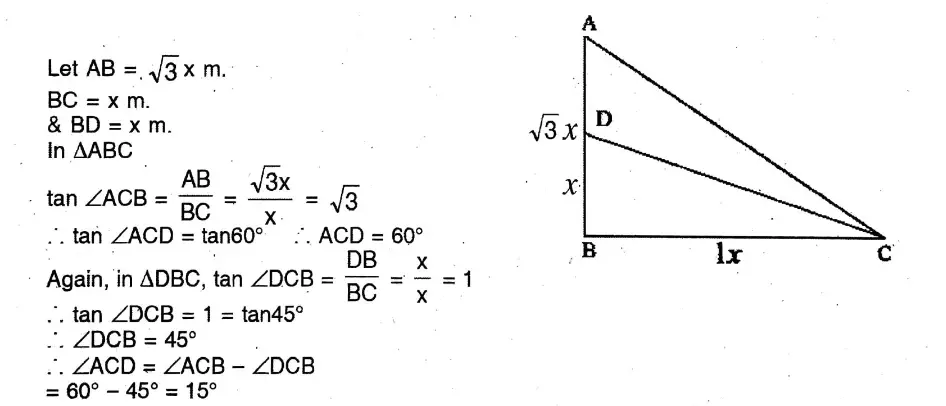
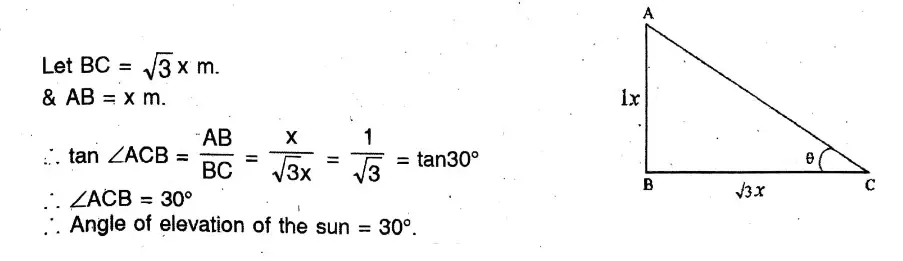
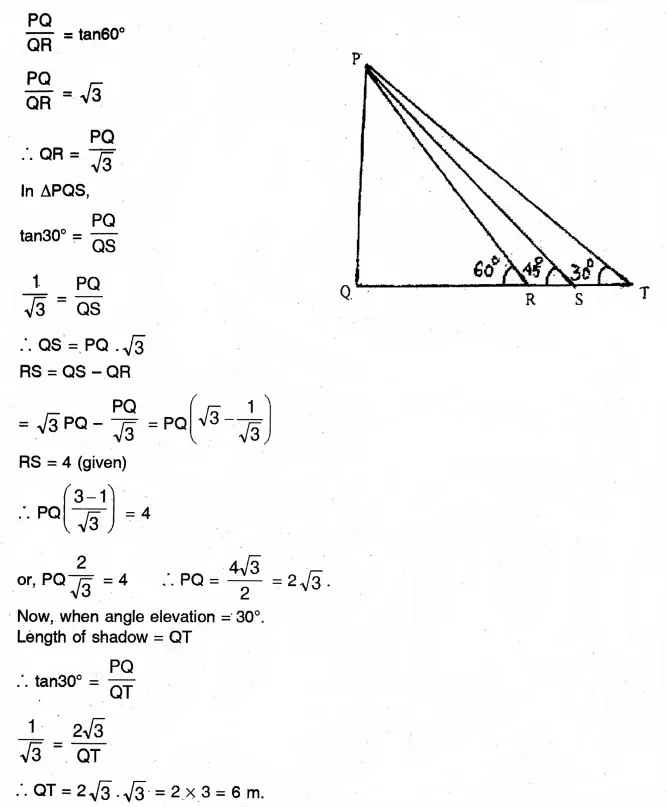
Or, When the angle of elevation of the sun changes from 45° to 60°, the length of shadow of a telegraph post changes to 4 metres. When the angle of elevation of the sun is 30°, then find the length of shadow of the telegraph post.

Solution: In APQR

 

Question 13. Answer any two questions:

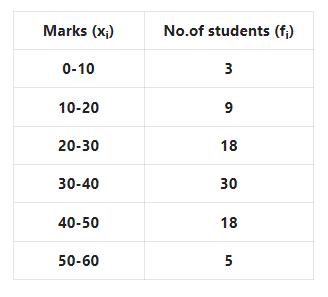
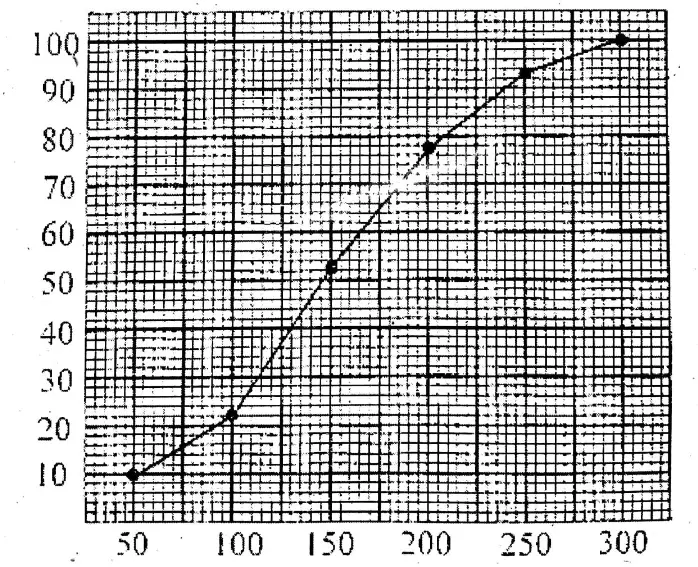
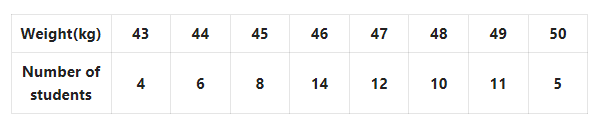
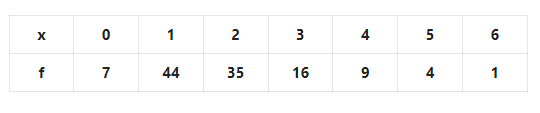
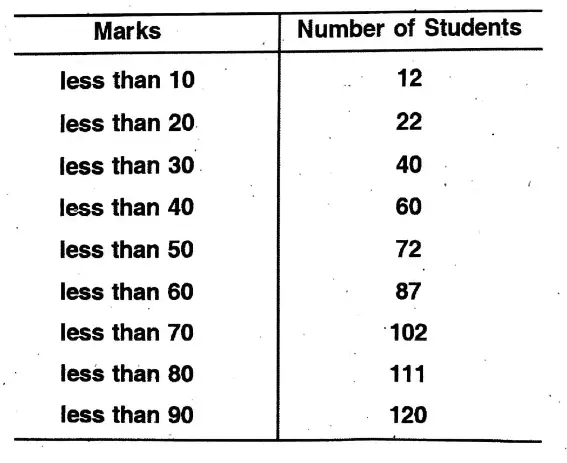
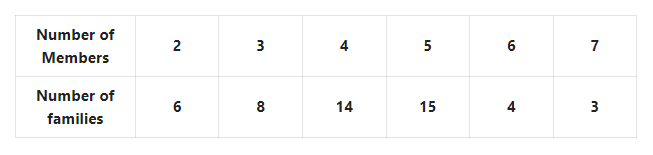
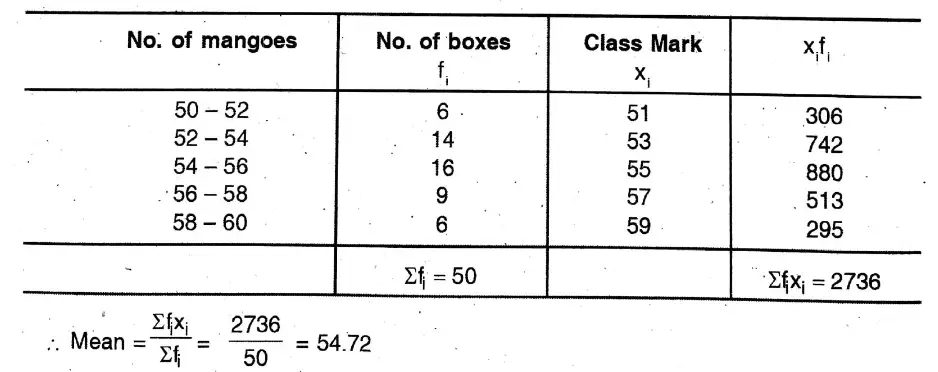
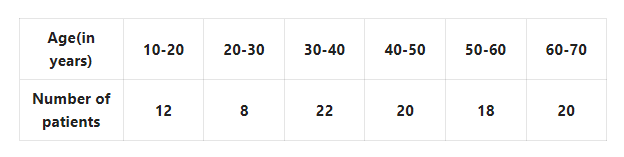
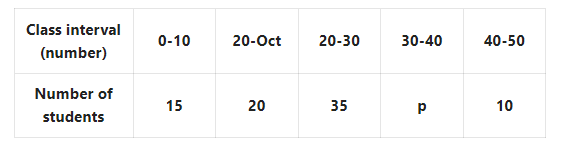
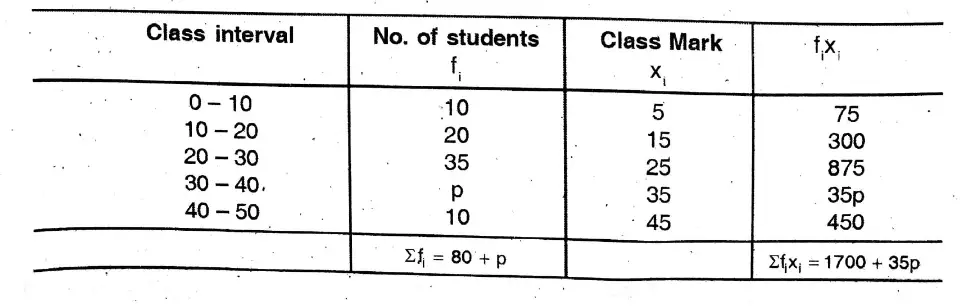
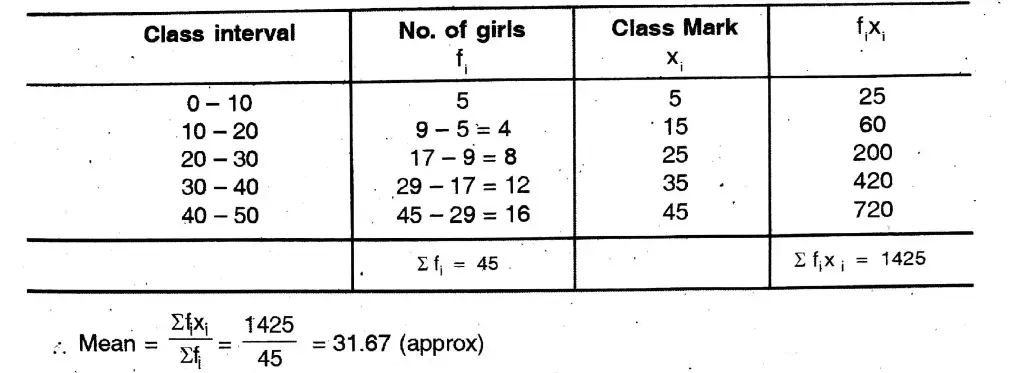
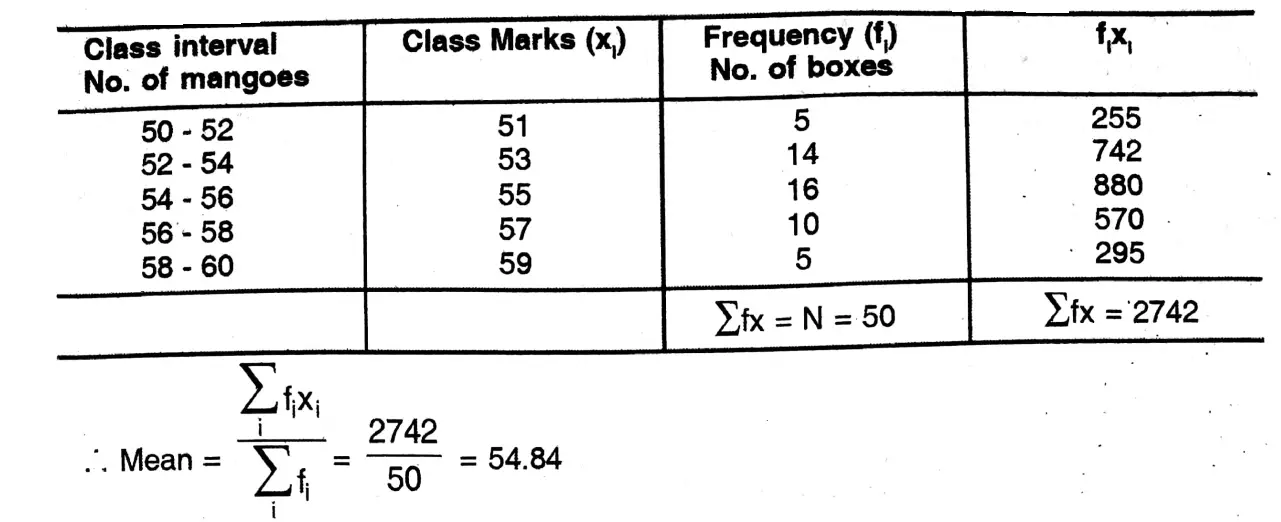
1. Shakil babu would bring mangoes kept in 50 packing boxes in the retail market. These boxes contained varying number of mangoes. The following is the distribution of mangoes according to the number of boxes.

 

 

Find the mean number of mangoes kept in 50 packing boxes.

Solution:

 

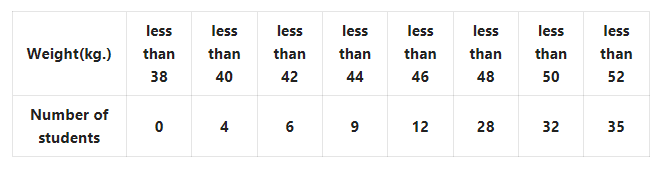
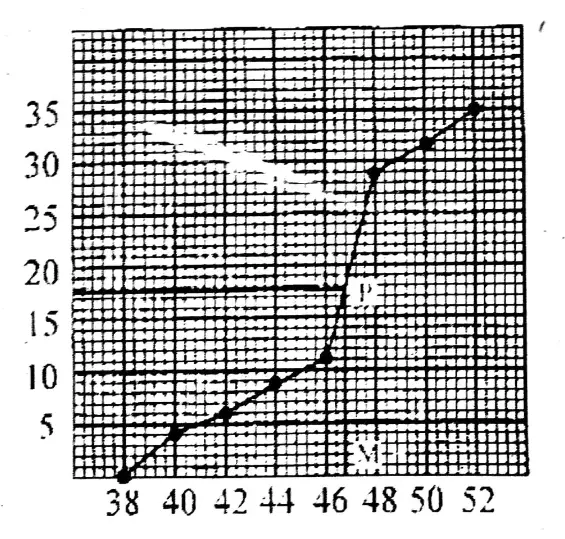
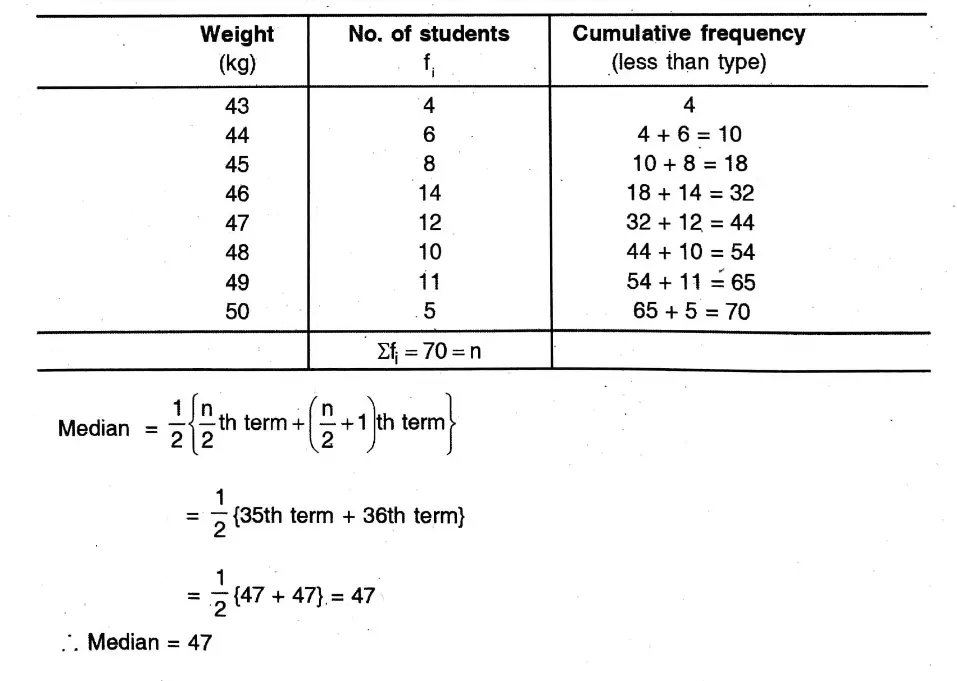
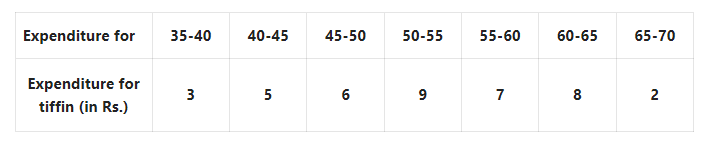
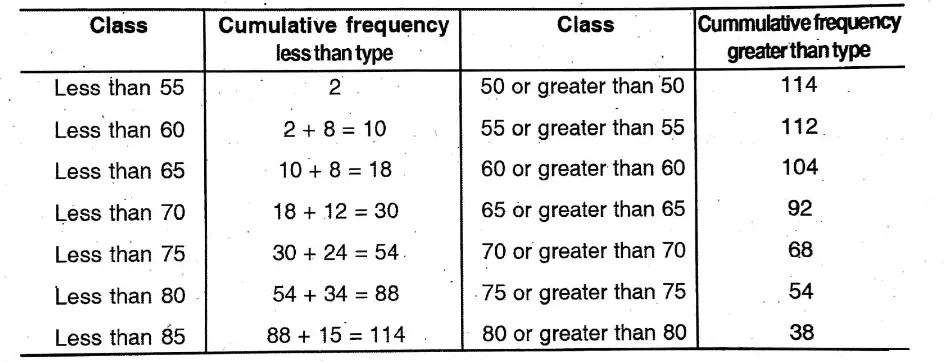
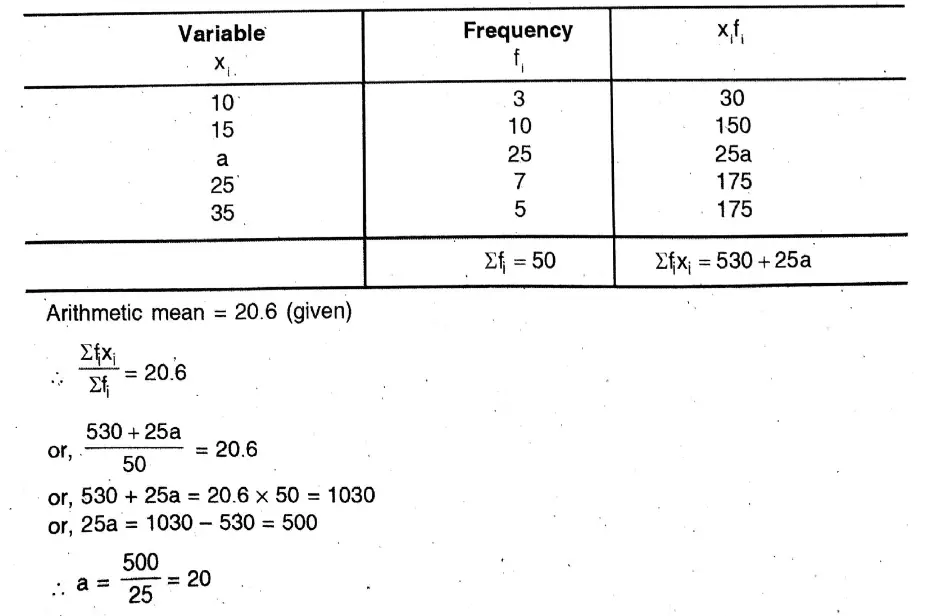
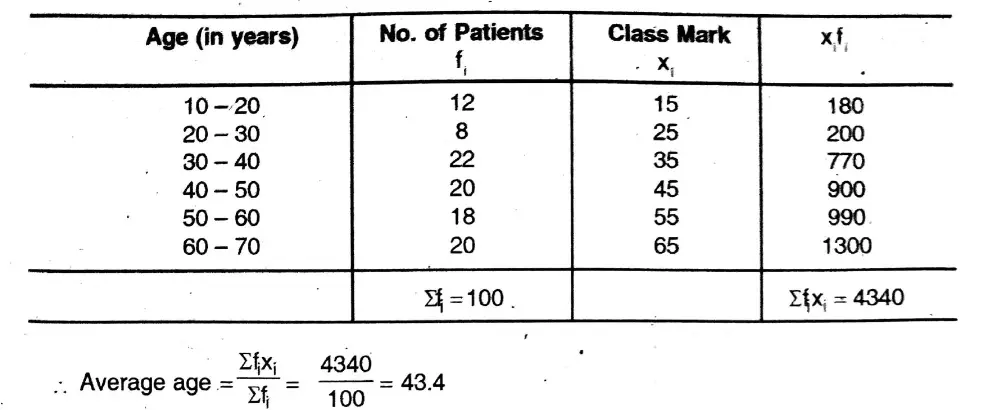
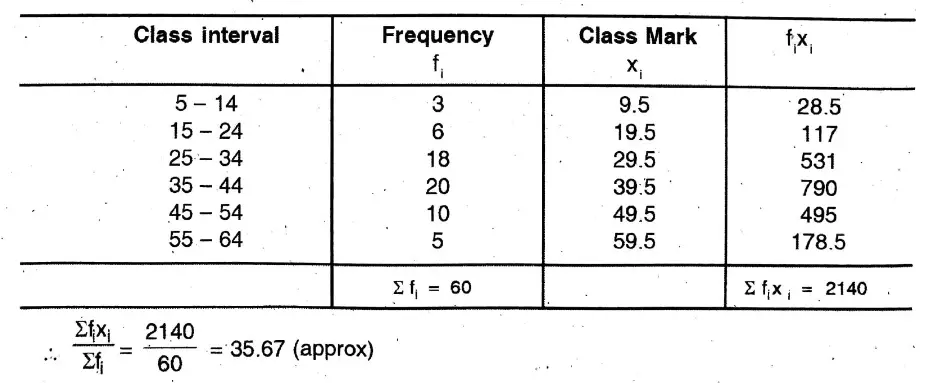
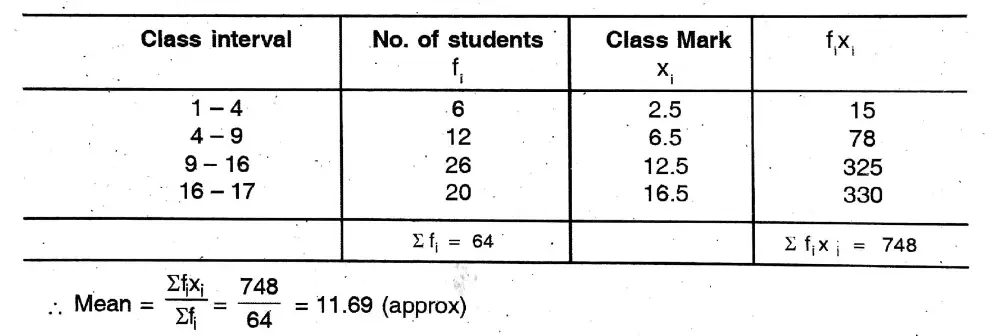
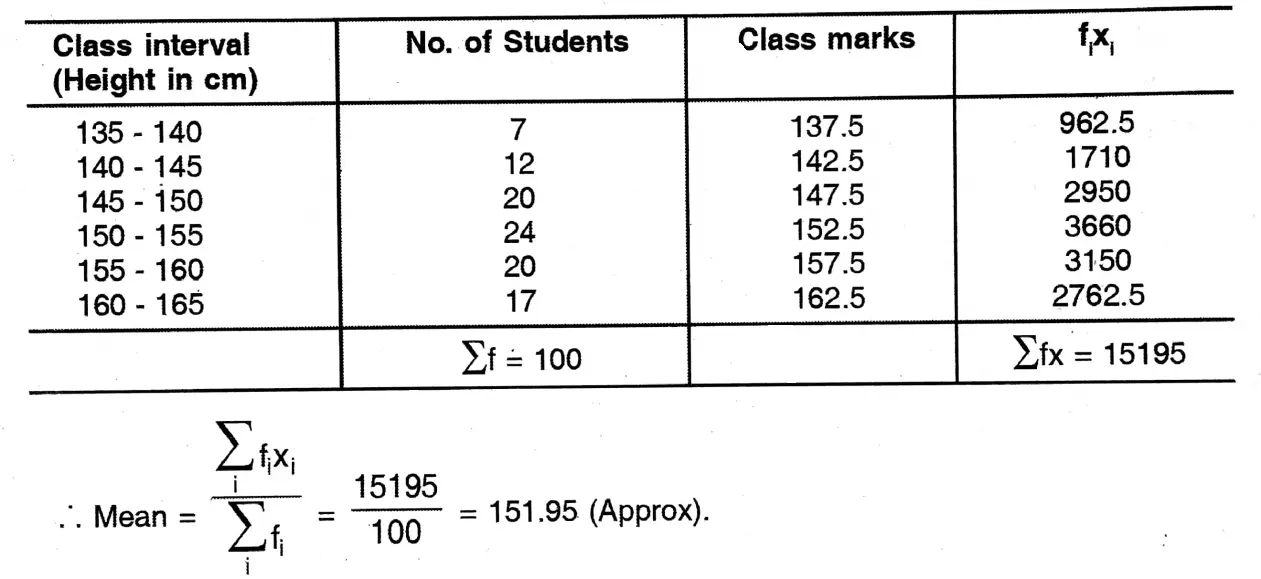
2. Find the mean of heights of students from the following distribution table

 

 

Solution:

 

 

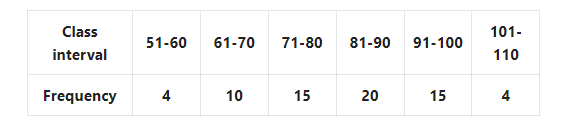
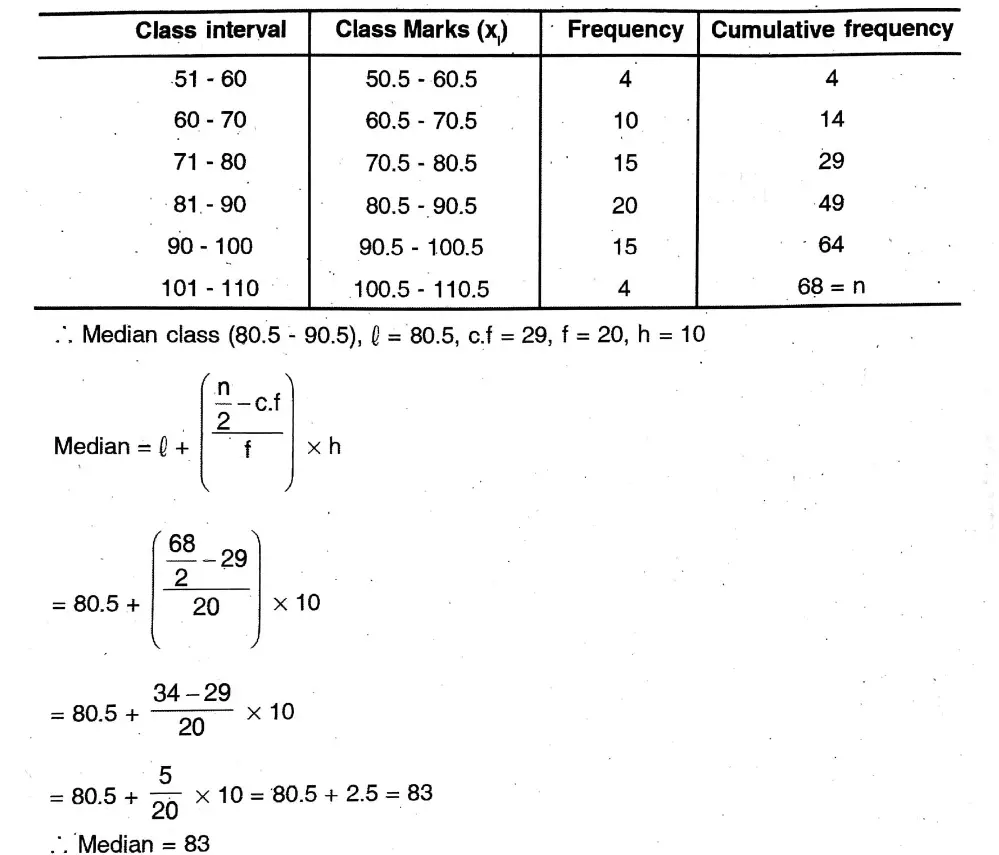
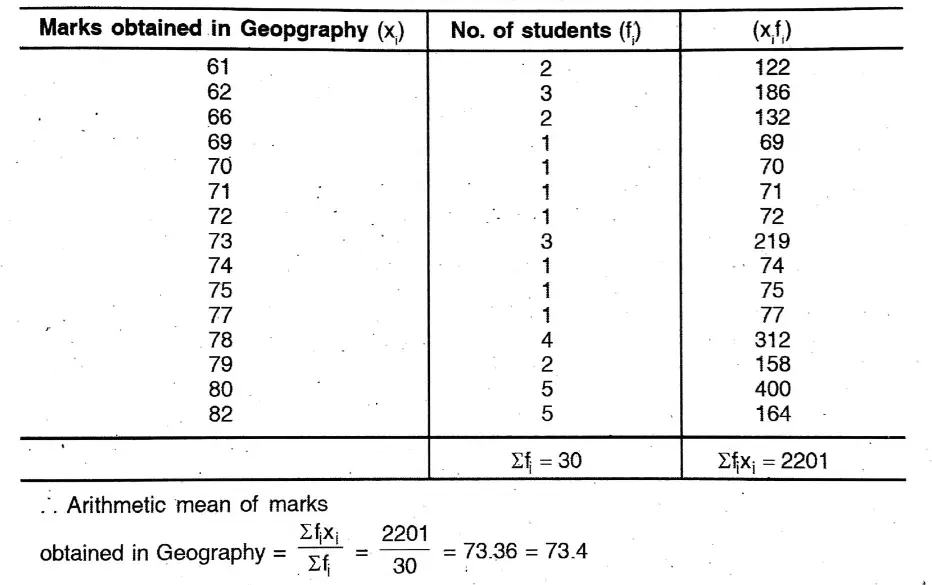
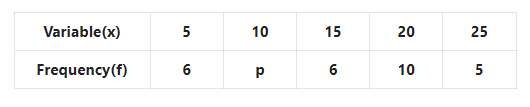
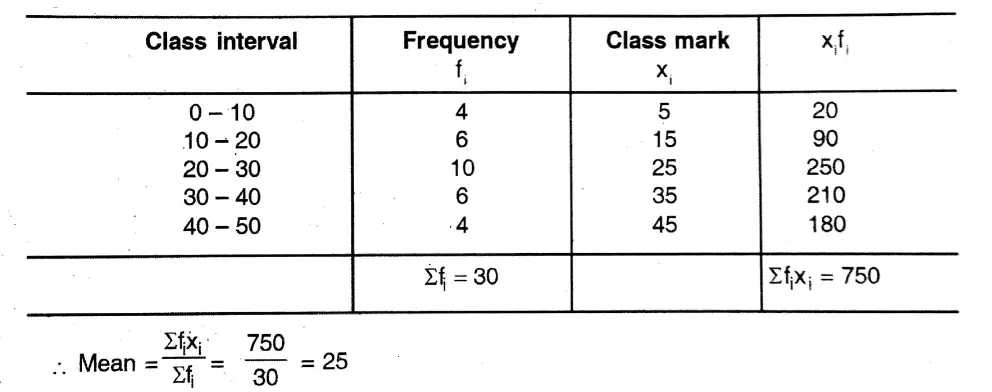
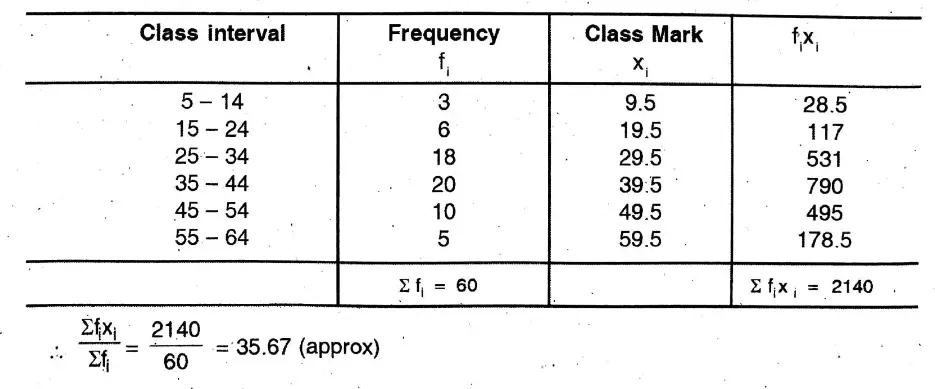
3. Find the mode of the following frequency distribution table

 

 

Solution:

 

 

 

 

 

 

Model Question Paper 2023 Mathematics set 2

 

Model Question Paper 2023 Mathematics set 2 MCQs

 

Question 1. Sum of the two roots of equation 5x² – 2x + 1 = 0 is

1. 2
2. 1
3. 1/2
4. 2/5

Solution:

Given

5x² – 2x + 1 = 0

Sum of the two roots of equation = -b/a

= -(-2/5)

= 2/5

Answer. 4. 2/5

Question 2. Samir invests Rs. 4,000 for 3 months and Amita invests Rs. 3,000 for 5 months in a business. Profit will be distributed in the ratio

1. 4:3
2. 3:4
3. 4:5
4. 5:4

Solution:

Given

Samir invests Rs. 4,000 for 3 months and Amita invests Rs. 3,000 for 5 months in a business.

Ratio of profit = 4000 x 3: 3000 x 5 = 12:15=4:5

Answer. 3. 4:5

Question3. x x 1/y and y = 2/5 when x = 5; x = 1/6 the value of y is

1. 1/3
2. 6
3. 12
4. 18

Solution : x = k/t or,5 = k 5/2

.. k = 2

Y = k/x = 2/½

= 12

The value of y is = 12

Answer. 3. 12

Question 4. In the adjoining figure, AB is the diameter of a circle with center O. If ZADC = 140° and /CAB = x°, the value of x is

1. 80°
2. 40°
3. 50°
4. 30°

Solution: CAB = x.x + 40° +90° = 180°

∴ x = 50°

Answer. 3. 50°

 

Question 5. If the length of the tower and the length of the shadow of a stick having a length of 20 meters are 50 meters and 10 meters respectively, the length of the tower is

1. 120 m.
2. 250 m.
3. 25 m.
4. 100 m.

Answer. 4. 100 m.

Given

If the length of the tower and the length of the shadow of a stick having a length of 20 meters are 50 meters and 10 meters respectively,

The length of the tower is 100 m.

Question 6. If the height of a solid right circular cone is 15 cm and the length of the diameter of the base is 16 cm, then the area of the lateral surface is

1. 120 sq cm.
2. 240π sq cm.
3. 136π sq cm.
4. 130π sq cm.

Solution: лгl= л x 8 x 17 sq cm

If the height of a solid right circular cone is 15 cm and the length of the diameter of the base is 16 cm

= 136л sq cm.

The area of the lateral surface is  130 sq cm.

Answer. 4. 130 sq cm.

Question 7. If the total surface area of a solid hemisphere is 1477, the length of the radius of the base of the hemisphere is

1. 14 cm.
2. 7 cm.
3. 21 cm.
4. 7.5 cm.

Solution: 3r2 = 147

If the total surface area of a solid hemisphere is 1477

∴ r=7

Answer. 2. 7 cm.

The length of the radius of the base of the hemisphere is 2. 7 cm.

 

Question 2. Answer the following questions :

1. If Α α 1/C and C α 1/B, find the variation relation between A and B.

Solution: A α 1/C       .. A= K₁ /C

C α 1/B    .. C = K₂/B     (K₁ & K₂ are constant)

A = K₁/K₂B     ∴ Aα B.

2. Fill in the blanks

1. If a straight line intersects the circle at the two points, this straight line is called the Intercept of the circle.

2. The length of the radii of the two circles are 4 cm and 5 cm. If two circles touch each other externally, the distance between the two centers is  9 cm.

3. If the surface area of a sphere is S and the volume is V, write the value of S³/V².

Solution:  S³/V²= 64л³r⁶/ 64/27л²r⁶

= 27π

Answer: 27π.

 

4. The lateral surface area of ae is √5 times its base area. Find the ratio between the height of the cone and the length ctius of its base.

Solution: 

Answer: 2/1

Question 3. Shova, Masud, and Rabeya started a business with a capital of Rs. 3,000, Rs. 3500, and Rs. 2500 respectively. They have decided to divide part 1/3 of the total profit equally and the remaining profit in the ratio of their capital invested. What will be the share of profit of each of them if the amount of profit at the end of the year is Rs. 810? 

Solution:

Shova, Masud, and Rabeya started a business with a capital of Rs. 3,000, Rs. 3500, and Rs. 2500 respectively. They have decided to divide part 1/3 of the total profit equally and the remaining profit in the ratio of their capital invested.

The ratio of capitals of Shova, Masud & Rabeya are

3000 :3500 :2500 = 30: 35: 25=6:7:5

Total Profit = Rs. 810

profit = Rs. 810 x 1/3

= Rs. 270.

Of Rs. 270, each will get = Rs. 270 ÷ 3 = Rs. 90. 

The rest of the profit= is Rs. (810270) = Rs. 540.

Out of Rs. 540,

Shova will get = 6/6+7+5 x Rs. 540 

= 6/18 × 540 

= Rs. 180

Masud will get= 7/18 x Rs. 540 

= Rs. 210

& Rabeya will get = 5/18 x Rs. 540 

= Rs. 150

∴ Shova will get = Rs. (90+ 180) 

= Rs. 270

Masud will get in total = Rs. (90+210) 

= Rs. 300

& Rabeya will get in total = Rs. (90+150) 

= Rs. 240

 

Or, Shakil and Mohuya jointly started a business with a capital of Rs. 30,000 and Rs. 50,000 respectively. After 6 months Shakil invested Rs. 40,000 more in the business, but Mohuya withdrew Rs. 10,000 for personal needs. If the profit amount is Rs. 19,000 at the end of the year, how many shares of profit each of them should get?

Solution:

Given

Shakil and Mohuya jointly started a business with a capital of Rs. 30,000 and Rs. 50,000 respectively. After 6 months Shakil invested Rs. 40,000 more in the business, but Mohuya withdrew Rs. 10,000 for personal needs. If the profit amount is Rs. 19,000 at the end of the year

Ratio of Capitals of Shakil & Mohuya throughout the year

= Rs. (30,000 12+ 40000 6): Rs. (50,000 6+ 40,000 6)

= Rs. (3,60,000+ 2,40,000): Rs. (3,00,000+ 2,40,000)

= 6,00,000 5,40,000 

= 60 :54 = 10:9

Total profit= Rs. 19,000

Shakil will get = 10/10+9 Rs. 19,000 

= Rs. 10/19 19,000 

= Rs. 10,000. Ans.

Mahna will get = 9/10+9 Rs. 19,000 

= Rs. 9/19 19,000 

= Rs. 9,000. Ans.

Question 4. If a c b and b c c, show that a³b³+ b³c³+ c³a³ α abc(a³ + b³+ c³).

Solution: aα b or, a =K₁b

Or, Solve: x-2 / x+2 +6 (x-2 / x+6) = 1 ,(x ≠ -2,6)

Solution : x-2 / x+2 +6 (x-2 / x+6) = 1

 

 

Question 5. Prove that if two circles touch each other externally, then the point of contact will lie on the line joining the two centers.

Solution: 

Given: Two circles with centers A and B touch each other at a point P. To prove A, P, and B are collinear.

Construction: A, P, and B, P are joined

Proof: Two circles with centers A and B touch each other at a point P.

∴ There exists a common tangent at point P.

Let ST is the common tangent, which touches both circles at point P.

∴ ST is the tangent of a circle with center A and AP is the radius through the point of contact

∴ AP ⊥ ST

Again, ST is tangent to the circle with center B and BP is the radius through the point of contact.

∴ BP ⊥ ST

∴ AP and BP are both perpendicular to ST at some point P.

∴ AP and BP lie on the same straight line, i.e., A, P, and B are collinear.

 

 

Or, Prove that if a perpendicular is drawn from the vertex containing the right angle of a right-angled triangle on the hypotenuse, the triangles on each side of the perpendicular are similar to the whole triangle and are similar to each other. 

Solution: ABC is a right-angled triangle whose∠A is a right angle and from right angular point A, AD is perpendicular on the hypotenuse BC.

To prove:

1. ΔDBA and ΔABC are similar to each other.

2. ΔDAC and ΔABC are similar to each other.

3. ΔDBA and ΔDAC are similar to each other.

Proof: In ΔDBA and ΔABC,

∠BDA = <BAC = 90° and ∠ABD = ∠CBA. So remaining

∠BAD = ∠BCA

∴ ΔDBA and ΔABC are similar to each other.

[1 is proved]

Again, in ΔDAC and ΔABC,

∠ADC= <BAC = 90°

∠ACD = ∠BCA. So remaining ∠CAD =∠CBA

∴ ΔDAC and ΔABC are similar to each other.

[2 is proved]

ΔDBA and ΔABC are similar to each other.

Again, ΔDAC and ΔABC are similar to each other.

So, ΔDBA and ΔDAC are similar to each other.

[3 is proved]

 

Question 6. BAC=1 right angle of a right-angled triangle ABC. AD is perpendicular to ΔABC BC² hypotenuse BC. Prove that ΔΑΒC/ΔACD = BC²/AC².

Solution: In right-angled AABC, A = 90°, & AD is perpendicular on hypotenuse BC.

To prove: ΔΑΒC/ΔACD = BC²/AC².

Proof: ACD & ABC are equiangular.

 

Question 7. Draw a triangle of which the length of one side is 6.8 cm and measures of two angles adjacent to this side are 60° and 75° and draw the circumcircle of this triangle.

Solution: The constructed triangle is ABC whose AB = 6.8 cm,

BAC = 60° and ABC = 75°

The center of the circumcircle.

 

 

Or, Draw a circle with center O having a radius of 2.5 cm in length. Take a point P outside the circle at a distance of 5 cm. from ‘O’. Draw two tangents to the circle from point P.

Solution: In AP is a tangent to the circle with center O, from an external point A.

 

 

Question 8. Three spheres made of copper with radii of 3 cm, 4 cm, and 5 cm are melted and a large sphere is made. What is the length of the radius of the large sphere?

Solution:

Given

Three spheres made of copper with radii of 3 cm, 4 cm, and 5 cm are melted and a large sphere is made.

Volume of 1st sphere with radius 3 cm = π (3)³ cu cm.

The volume of the 2nd sphere with a radius of 4 cm = 4/3 π (4)³ cu cm.

& Volume of 3rd sphere with radius 5 cm = 4/3 π (5) cu cm.

Total volume of 3 small spheres = 4/3  π (3)³+ 4/3  π (4)³ + 4/3  π (5)³

= π(33 +43 +53) cu cm.

= π(27 +64 +125) cu.cm.

= 4/3 π x 216 cu cm.

Now, let the radius of the new big sphere = R cm.

Its volume = 4/3 πR³

According to the problem,

4/3πr³ = 4/3 π x 216

∴ R3 = 216

∴ R = 3√216

= 6 cm.

The length of the radius of the large sphere = 6 cm.

 

Or, If the length of the radius of the base is 12 meters and the height is 5 meters, what will be the cost to make a tent in the shape of the right circular cone at the rate of Rs. 3.50 per sq meter?

Solution:

Given

If the length of the radius of the base is 12 meters and the height is 5 meters

Here radius (r) = 12 m & height (h) = 5 m.

∴ Slant height (l) = √r²+h²

= √12² +5²

= √144+25

= √169

= 13 m.

Curved Surface area of cone

πrl= 22/7 x 12 x 13 sqm

= 3432/7 sqm.

∴ The total cost of making the tent at the rate of Rs. 3.5/sqm.

= Rs. 3.5 x 3432/7

= Rs. 1716. Ans.

 

 

 

 

Model Question Paper 2023 Mathematics set 1

 

Model Question Paper 2023 Mathematics set 1 MCQs

 

Question 1. Compound interest and simple interest are equal at the same rate of interest per annum in

1. 1 year
2. 2 years
3. 3 years
4. 4 years

Answer. 1. 1 year

Question 2. If the ratio of principal and simple interest is 10: 3, for 5 years, the rate of interest per annum will be 

1. 3
2. 30
3. 6
4. 12

Answer. 3. 6

Question 3. Which one is not a quadratic equation given below?

1. 2x-3×2 = 3×2 + 5
2. (2x+3)2=2(x2 – 5)
3. (√3 + 2)2 = 3×2-7
4. (x-2)2=5×2 + 2x – 3

Answer. 3. (√3 + 2)2= 3×2-7

Question 4. If the roots are equal to the quadratic equation 4×2 + 6kx+9= 0, the value of k

1. 2 or 0
2. -2 or 0
3. 2 or -2
4. only 0

Answer. 3. 2 or -2

Question 5. In the adjoining figure, ZOAB = 50° of a circle with center O and if C is any point on the circle, the value of ZACB is

1. 50°
2. 40°
3. 80°
4. 100°

Answer. 2. 40°

 

 

Question 6. AB and CD are two equal chords of a circle with center O. If ZAOB = 70°, the value of COD is

1. 110°
2. 70°
3. 35°
4. 80°

Answer. 2. 70°

Question 2. Answer the following questions:

1. In how many years the interest will be 3/4th of the principal at the rate of interest 10° simple interest per annum?

Solution : I = prh/100

3x/5 = x x 10 x h / 100

∴ t=6.

2. If p: q=5:7 and p-q=-4, what is the value of (3p – 2q)?

Solution: Let p = 5k, q = 7k

∴ 5k – 7k = -4

∴ k = 2

∴3p – 2q 

= 3 x 10-2 x 14

= 30-28 

= 2.

The value of (3p – 2q) = 2.

3. Two parallel chords of a circle with center O lie opposite to the center. If AB = 10 cm, CD = 24 cm, and if the distance between the two chords AB and CD is 17 cm, find the radius of that circle.

Solution:

Given

Two parallel chords of a circle with center O lie opposite to the center. If AB = 10 cm, CD = 24 cm, and if the distance between the two chords AB and CD is 17 cm

OD² = OP² + PD²

OB = OQ² + QB²

OD = OB      ∴ OP²+ PD² = OQ² + QB²

Let OP = x, OQ = 17 – x

x² + 12² = (17-x)² + x²

x² – 34x + 289 + x² = x² + 144

x²-34x+145 = 0

(x+29) (x-5)= 0

∴ x = 5

∴The radius of that circle = 5

 

4. In the adjoining figure find the value of x.

Solution: BDC = BAC = 35

In ∠BCD, ∠BDC + 75° + x = 180°

or, 35° + 75 + x = 180°

∴ x = 180-110 = 70.

5. If the volume of a cube is 512 cubic cm, find the total surface area of that cube. 

Solution: a³ = 512    Where a = one side

a = √5128 cm.

Total Surface area = 6a² = 6 (8)² = 384 square.

 

Question 3. In how many years will Rs. 1,00,000 amounts to Rs. 1,33,100 at 10% compound interest per annum.

Solution:

Or, The length of a tree increases by 20% every year; if the present length of the tree is 28.8 meters, let us find what was the length three years before.

Solution:

 

Question 4.

1. (2x+1) + 3/2x+1 = 4, (x ≠ – 1/2)

Solution:

 

2. 1/(x-2)(x-4) + 1/(x-4)(x-6) + 1/(x-6)(x-8) + 1/3 = 0, (x≠2,4,6,8)

Solution:

Given

 

Question 5. Sujata drew a right-angled triangle having a hypotenuse of 13 cm in length, and the difference between the other two sides is 7 cm. Find the length of the other two sides of a right-angled triangle drawn by Sujata.

Solution:

Given

Sujata drew a right-angled triangle having a hypotenuse of 13 cm in length, and the difference between the other two sides is 7 cm.

Let AB = x cm & BC = x – 7

∴ AB2+ BC2 = AC2

x2+(7-x)2 = 132

or, x2 +49 + x2 – 14x = 169

or, 2×2- 14x-120 = 0 or, x2-7x-60 = 0

(x-12) (x+5)=0

∴ x-12=0

x = 12

One side = 12 cm another side = 12-75 cm.

Or, If a two-digit positive number is multiplied by its unit digit, the value of the product is 189 and the tens digit is twice its unit digit, find the unit digit of the number. Solution: Let two-digit number = 10y + x

Given

If a two-digit positive number is multiplied by its unit digit, the value of the product is 189 and the tens digit is twice its unit digit

∴ According to the given conditions,

(10y+x) x = 189

x²+10xy = 189         & y = 2x

10x. 2x + x² = 189

20x²+ x² = 189

21x² = 189

189/21 = 9

∴ x = √9

= 3

y = 6

Required number = 10y+ x = 63.

Question 6. If a, b, c, d are in continued proportion, prove that (a² + b² + c²) (b² + c² + d²) = (ab + bc + cd)²

Solution: Let = a/b = b/c = c/d = k

∴  a = bk, b = ck, c = dk

 L.H.S. = (b²k²+ c²k² + d²k²) (c²k² + d²k² + d²)

= (c²K⁴+ c²k² + d²k²) (d²K⁴+ d²k² + d²k² + d²)

= (d²k + d²K⁴+ d²k²) (d²K⁴+ d²K⁴+ d²k² + d²k² + d²) d²k²(K⁴+k² + 1) d²(k + k² + 1)

= d⁴k²(k + k² + 1)²

R.H.S. = (ab + bc + cd)²

= (bkb + ck.c + dk.d)²

= (b²k + c²k + d²k)²

= (d²k⁶+ d²k³ + d²k)²

= {d²k(K⁴+ k²+ 1)}²

=d⁴k²(K⁴+k² + 1)2 

∴ L.H.S. = R.H.S.

 

Or, if a = √5+1/√5-1 and ab= 1, find the value of(a/b +b/a)

Solution: a = √5+1/√5-1

Question 7. Prove that the angle at which an arc of a circle subtends at the center is double any angle subtended by it on the circle.

Solution:

Given: ∠AOB is the angle at the center of the circle with center O and ∠ACB is the angle at any point on the circle formed by circular arc ZAPB.

To Prove: ∠AOB = 2∠ACB

According to the length of the circular arc APB, these may be of three types. In 1 and APB are minor arcs. In 2 APB is a semi-circular arc, and in 3 APB is a major arc.

Construction: C and O are joined and CO is extended up to point D.

Proof: In ΔAOC, OA = OC in each case [radii of the same circle]

∴ ∠OCA = ∠OAC

Again, in each case, the side CO of ΔAOC is extended up to point D. Exterior ∠AOD = ∠OAC + ∠OCA

=2∠OCA——(1)                [ ∠OAC = ∠OCA]

In ΔBOC, OB OC in each case [radii of the same circle] Again, since side CO of ABOC is extended up to point D.

∴ Exterior BOD = ∠OCB +∠OBC

= 2∠OCB——-(2)              [ ∠OBC = ∠OCB]

In 1 and 2 ∠AOD + ∠BOD = 2∠OCA + 2∠OCB [we get from 1 & 2]

∴ ∠AOB = 2(∠OCA + ∠OCB) = 2∠ACB (3)

∴ ∠AOB = 2∠ACB

In 4 BOD ∠AOD = 2∠OCB-2∠OCA

Or, ∠AOB = 2∠OCB-2∠OCA

Or, ∠AOB = 2(∠OCB – ∠OCA)

∴ ∠AOB = 2∠ACB. Proved.

 

Or, Prove that the line drawn through the center of a circle bisects a chord, which is not a diameter, is perpendicular to the chord.

Solution :

Given AB is a chord of the circle with its center at O, which is

not a diameter, and OD, is perpendicular to the chord AB.

To prove: CD, bisects the chord AB, i.e., AD = DB. Construction: O, A, and O, B are joined.

Proof: OD is perpendicular to the chord AB.

∴ ΔODA and ΔODB are right-angled triangles.

∴ In right-angled ΔODA and ΔODB, ΔODA =ΔODB (Each is a right angle)

Hypotenuse OA = Hypotenuse OB [radii of the same circle] and OD is a common side.

∴ ΔODA

ΔODB [By R.H.S. axiom of congruency]

∴ AD = DB [Corresponding sides of the congruent triangles] Proved.

Question 8. A reservoir of 21 dcm in length, 11 dcm in breadth, and 6 dcm in depth are filled half with water. How much dem will the water level be raised if 100 iron balls each of which has a 21 cm diameter be completely immersed in it?

Solution:

Given

A reservoir of 21 dcm in length, 11 dcm in breadth, and 6 dcm in depth are filled half with water.

Radius of cylinder (r) = 21/2 cm. 

The volume of one cylinder π(21/2)² x 20 cu cm.

The volume of 100 cylinders = 100 x π x (21/2)² x 20 cu cm.

Let the level of water increase by x dcm. 

The volume of 100 cylinder = Volume of increased water

or, 100 x л x (21/2)² x 20

= 210 x 110 x 10x

x = 100 x 22/7 x 21/2 x 21/2 x 20  /  210 x 110 x 10

= 30 cm 

= 3 dcm.

 

Or, The ratio of the height of a right circular solid cylinder and the length of the radius of the base is 3:1. If the volume of the cylinder is 1029 π cubic cm, what will be the total surface area of the cylinder?

Solution:

Given

The ratio of the height of a right circular solid cylinder and the length of the radius of the base is 3:1. If the volume of the cylinder is 1029 π cubic cm,

Let height = 3x, and radius = x

∴ Volume = x². 3x = 1029

∴ 3x² = 1029

x³= 343 

∴ x = 7

∴ radius = 7 cm, height = 3 x 7 = 21 cm.

Total surface area

= 2 Area of base + Surface area

= 2 πг² + 2πгh

= 2лr(г + h)

= 2 x 22/7 x 7(7+21)

= 44 x 28 sq cm. 

= 1232 sq cm.

Total surface area of the cylinder = 1232 sq cm.

 

 

West Bengal Board Class 10 Math Book Solution In English

Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4

Question 1. Paid amounts a day of our 16 friends for going to school and other expenditures are:

15, 16, 17, 18, 19, 17, 15, 15, 10, 17, 16, 15, 16, 18, 11

Let us find the mode of paid amounts of a day of our friends. 

Solution: Arranging the given data in ascending order, we get 10, 11, 15, 15, 15, 15, 16, 16, 16, 17, 17, 17, 17, 18, 19. We see 15 & 17 occur a maximum number of times.

∴ Mode = Rs. 15 & Rs. 17.

Read and Learn More WBBSE Solutions For Class 10 Maths

Question 2. The heights (cm) of some students in our class are given below. 131, 130, 130, 132, 131, 133, 131, 134, 131, 132, 132, 131, 133, 130, 132, 133, 135, 131, 135, 131, 130, 132, 135, 134, 133. Let us find the mode of the heights of students.

Solution: Arranging the given data in ascending order, we get

130, 130, 130, 130, 131, 131, 131, 131, 131, 131, 131, 132, 132, 132, 132, 132, 133, 133, 133, 134, 134, 135, 135, 135, 135.

Here 131 occurs a maximum number of times.

∴ Mode = 131 cm.

West Bengal Board Class 10 Math Book Solution In English

Question 3. Let us find the mode of data given below :

1. 8, 5, 4, 6, 7, 4, 4, 3, 5, 4, 5, 4, 4, 5, 5, 4, 3,3, 5, 4, 6, 5, 4, 5, 4, 2, 3, 4.

Solution: Arranging the given data in ascending order we get

2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 7, 8. 

Here 4 occurs a maximum number of times.

∴ Mode = 4

2. 15, 11, 10, 8, 15, 18, 17, 15, 10, 19, 10, 11,10, 8, 19, 15, 10, 18, 15, 3, 16, 14, 17, 2

Solution: Arranging the given data in ascending order we get,

2, 3, 8, 8, 10, 10, 10, 10, 10, 11, 11, 14, 15, 15, 15, 15, 15, 16, 17, 17, 18, 19, 19. 

Here 10 and 15 occur a maximum number of times.

∴ Mode = 10 and 15

Question 4. The frequency distribution table shows the selling prices of shoes from a special shoe shop company in our village.

Solution:

Here are 5 persons for size 4 & 5 persons for size 6.

∴ Mode = 4 & 6.

Question 5. Let us find the mode from the following frequency distribution table of the ages of examinees of an entrance examination.

Solution:

Here Modal class = (18 – 20)

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)     Here l = 18

= \(18+\left(\frac{75-45}{150-45-38}\right) \times h\)             f₁ = 75 

= \(18+\frac{30}{67} \times 2\)            f₂ = 38

Mode = 18 + 0.9 = 18.9 (approx)        h = 2

Question 6. Let us see the frequency distribution table of obtaining marks in a periodical examination of 80 students in a class and let us find the mode.

Solution:

Here, Modal class = (20 – 25)

l = 20, f₁ = 22, f₀ = 16, f₂ = 1, h = 5

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h=20+\frac{22-16}{44-11-11} \times 5\)

= \(20+\frac{6}{17} \times 5\)

= 20 + 1.76

Mode = 21.76 (approx)

 

Question 7. Let us find the mode of the frequency distribution table given below

Solution:

∴ Modal class = 15 – 20,

∴ l = 15, h = 5

f₁ = 28, f₀ = 18, f₂ = 17, h = 5

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)

= \(15+\frac{28-18}{56-18-15} 5\)

= \(15+\frac{10 \times 5}{21}\)

= 15 + 2.38

Mode = 17.38

 

Question 8. Let us find the mode of the frequency distribution table given below

Solution:

∴ Modal class = 75 – 84,

∴ l = 75, h = 9

f₁ = 32, f₀ = 19, f₂ = 12

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)

= \(75+\frac{32-19}{64-19-12} \times 9\)

= \(75+\frac{13 \times 9}{33}\)

= 75 + 3.54

Mode = 78.54 (approx)

WBBSE Solutions Guide Class 10 Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4 Multiple Choice Questions

Question 1. The median of a given frequency distribution is found graphically with the help of 

1. Frequency curve
2. Frequency polygon
3. Histogram
4. Ogive

Answer. 4. Ogive

Question 2. If the mean of numbers 6, 7, x, 8, and y, is 9, then

1. x + y = 21
2. x + y = 19
3. x – y = 21
4. x – y = 19

Answer. 2. x + y = 19

Question 3. If 35 is removed from the data 30, 34, 35, 36, 37, 38, 39, 40 then the median increases by

1. 2
2. 1.5
3. 1
4. 0.5

Answer. 4. 0.5

Question 4. If the mode of data 16, 15, 17, 16, 15, x, 19, 17, 14 is 15, then the value of x is 

1. 15
2. 16
3. 17
4. 19

Answer. 1. 15

WBBSE Solutions Guide Class 10 Question 5. If the median of arranging the ascending order of data 8, 9, 12, 17, x + 2, x + 4, 30, 31, 34, 39, is 15, then the value of x is

1. 22
2. 21
3. 20
4. 24

Answer. 2. 21

WBBSE Solutions Guide Class 10 Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4 Fill In The Blanks

1. Mean, median, and mode are the measures of  Central tendency

2. x_1,x_2,x_3…….. x_{n is} x‾ _{, mean of} ax_1, ax_2, ax_{3…………} ax_{n is} ax¯

3. At the time of finding the arithmetic mean, the lengths of all classes are Equal.

WBBSE Solutions Guide Class 10 Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4 Short Answers

Question 1

Let us find the difference between the upper-class limit in the median class and the lower-class limit of the modal class of the above frequency distribution table.

Solution: n = 77, n/2 = 38.5

Median class= 125-145

The upper limit of Median class = 145

Model class= 125-145

Lower class limit of Modal class = 125

∴ Required Difference 145 125 = 20.

Question 2. The following frequency distribution shows the time taken to complete a 100-meter hurdle race of 150 athletics :

Let us find the difference between the upper-class limit of the modal class and the lower-class limit of the modal class.

Solution:

Question 3. The mean of a frequency distribution is 8.1, if Σf₁x₁= 132 + 5k and Σf₁ = 20, let us find the value of k.

Solution:

Given

The mean of a frequency distribution is 8.1, if Σf₁x₁= 132 + 5k and Σf₁ = 20

\(\frac{\sum f_i n_i}{\sum f_i}=8.1\) \(\frac{132+5 k}{20}=8.1\)

or, 132 + 5k = 162

∴ 5k = 30

∴ k = \(\frac{30}{5}\) = 6

 

Question 4. If u_i =x_i-25 / 10 Σf_iu_i = 20 and Σf_i = 100, let us find the value of x.

Solution:

If u_i =x_i-25 / 10 Σf_iu_i = 20 and Σf_i = 100

a = 25, h = 10

∴ \(\mathrm{n}=\mathrm{a}+\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{n}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\)

= \(25+10 \times \frac{20}{100}=25+2=27\)

Question 5.

Let us write the modal class from the above frequency distribution table.

Solution:

∴ Model Class = (30-40)

Maths WBBSE Class 10 Solutions Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.3

Question 1. The following distribution table shows the daily profit (in Rs.) of 100 shops in our village.

Making a cumulative frequency table (less than type) of the given frequency table, let us draw Ogive on graph paper.

Solution:

Read and Learn More WBBSE Solutions For Class 10 Maths

Assuming on graph paper along the x-axis 1 small division= 1 unit & along the y-axis 1 small division = 1 unit, & plot the points (50, 10), (100, 26), (150, 54), (200, 76), (250, 94) & (300, 100); by joining the points, we get the Ogive less than type.

Question 2. The following data shows the weight of 35 students in the class of Nivedita.

Making cumulative frequency (less than type) distribution table, let us draw Ogive on graph paper and hence let us find the median from the graph. Let us find the median by using a formula and verify it.

Solution:

Here, n = 35

∴ \(\frac{n}{2}\) = \(\frac{35}{2}\) = 17.5

At the y-axis, find the point (0, 17.5)

Now plotting the points we draw the graph.

Perpendicular from the point (0, 17.5) cuts the graph at P.

Draw the perpendicular from P on the x-axis (P.M)

∴ M is the median.

The median class is (46-48).

∴ Median = \(\ell+\left[\frac{\frac{n}{2}-\mathrm{c} . f}{f}\right] \times h=46+\left(\frac{17.5-12}{16}\right) \times 2=46+\frac{5.5}{8}=46+0.69\)

Median = 46.69

Question 3.

Making cumulative frequency (greater than type) distribution table of given data, let us draw Ogive on graph paper.

Solution:

Plot the points (0, 45), (5, 41), (10, 31), (15, 16), (20, 8) & (25, 5), by joining then we got the Ogive.

Question 4.

Drawing less than Ogive and greater than type Ogive of given data along the same axes, on the graph paper, let us find the median from the graph.

Solution:

For less than type Ogive, plot the points (120, 12), (140, 26), (160, 34), (180, 40) & (200, 50), by joining them we get the Ogive (less than type).

For greater than type Ogive, plot the points (100, 50), (120, 38), (140, 24), (160, 16) & (180, 10), by joining them we get Ogive (greater than type)

The median from the graph = 139 (Approx.)

Application 1. Let us find the mode of the data given below.

1. 2, 3, 5, 6, 2, 4, 2, 8, 9, 4, 5, 4, 7, 4, 4

2. 11, 27, 18, 26, 13, 12, 9, 15, 4, 9

3. 102, 104, 117, 102, 118, 104, 120, 104, 122, 102

4. 5, 9, 18, 27, 15, 5, 8, 10, 16, 5, 7, 5

Solution:  Let us write the number of given data in ascending order of magnitude

1. 2, 3, 5, 6, 2, 4, 2, 8, 9, 4, 5, 4, 7, 4, 4

We see 4 occur a maximum number of times

The mode = 4

2. Let us write the number of given data in ascending order of magnitude. 4, 9, 9, 11, 12, 13, 15, 18, 26, 27

We see 9 occurs a maximum number of times.

∴The mode = 9

3. Write the number of given data in ascending order 102, 102, 102, 104, 104, 104, 117, 118, 120, 122.

Here 102 & 104 occur a maximum number of times.

∴The mode = 102 & 104

4. Write the number of given data in ascending order.

5, 5, 5, 5, 7, 8, 9, 10, 15, 16, 18, 27

Here 5 occurs a maximum number of times.

∴ The mode = 5

Application 2. The mode of frequency distribution table is given below.

Solution:

Maximum frequency 24

∴ Modal class = 12 – 15

Here l = 12, f₁ = 24, f₀ = 12, f₂ = 21, h = 15 – 12 = 3

∴ Mode = \(\ell+\left[\frac{f_1-f_0}{2 f_1-f_0-f_2}\right] \times h\)

= \(12+\left[\frac{24-12}{2 \times 24-12-21}\right] \times 3\)

= \(12+\frac{12}{48-33} \times 3\)

= \(12+\frac{12}{15} \times 3\)

Mode= 12 + 2.4 = 14.4

Ganit Prakash Class 10 Solutions Pdf In English

Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.2

Question 1. Per day selling prices (in Rs.) of Madhu’s uncle’s shop for the last week were 107, 201, 92, 52, 113, 75, and 195; let us find the median of the selling prices.

Solution: Selling prices (in Rs.) per day are 107, 207, 92, 52, 113, 75, and 195. To find the median of the selling prices first arrange them in ascending order, we get 52, 75, 92,107, 113, 195, and 210.

Here n = 7 (odd).

∴ Median = (7+1/2) th term 

= 4th term 

= 107

∴ Median Rs. 107

Read and Learn More WBBSE Solutions For Class 10 Maths

Question 2. If the ages (in years) of some animals are 6, 10, 5, 4, 9, 11, 20, or 18; let us find the median of ages.

Solution: Ages (in years) of some animals are 6, 10, 5, 4, 9, 11, 20, 18.

Arranging in ascending order, 

we get 4, 5, 6, 9, 10, 11, 18, 20

Hére n = 8 (even).

Median = 1/2 {n/2 th term + (n/2 + 1) term}

= 1/2 (4th term + 5th term)

= 1/2(9+10) 

= 19/2

= 9.5 years

Question 3. The marks obtained by 14 students are 42, 51, 56, 45, 62, 59, 50, 52, 55, 64, 45, 54, 58, and 60; let us find the median of the marks obtained.

Solution: The marks obtained by 14 students are 42, 51, 56, 45, 62, 59, 50, 52, 55, 64, 45, 54, 58, and 60. 

Arranging in ascending order, we get 42, 45, 45, 50, 51, 52, 54, 55, 56, 56, 58, 59, 60, 62.

Here, n = 14 (even).

Median = 1/2 {n/2 th term + (n/2 + 1) term}

= 1/2 {7th term + 8th term}

= 1/2(54+55)

= 1/2 x 109

= 54.5

∴ Median = 54.5

Question 4. Today the scores of the cricket match in our locality are Let us find the median of scores in our cricket match. 

Solution: By arranging the scores of the match

6 6 6 77777 88888 99999 10 10 11 11

Here n = 22 i.e., even.

∴ Median = 1/2 {n/2 th term + (n/2 + 1) term}

= 1/2 (11th term + 12th term}

= 1/2 (8+8)

= 1/2 x16

= 8

∴ Median = 8

Question 5. Let us find the median weight from the following frequency distribution table of 70 students.

Solution:

Question 6. Let us find the median of the length of diameter from the following frequency distribution table of the length of the diameter of the pipe.

Solution:

Question 7. Let us find the median.

Solution:

Question 8. The frequency distribution table of expenditures of tiffin allowances of 40 students is given below.

Let us find the median of tiffin allowance.

Solution:

Question 9. Let us find the median heights of students from the table below.

Solution:

Here, l – 150, c.f. = 35, f = 22, h = 5.

∴ median = \(\dot{\ell}+\left[\frac{\frac{n}{2}-c . f}{f}\right] \times h\)

= \(150+\left[\frac{50-35}{22}\right] \times 5\)

= \(150+\frac{15}{22} \times 5\)

= 150 + 3.4

median  = 153.4 (approx)

 

Question 10. Let us find the median of data from the following frequency distribution table.

Solution:

Question 11. Let us find the median of the given data.

Solution:

Question 12. Let us find the median of the given data.

Solution:

Question 13. Let us find the median of the given data.

Solution:

Question 14. Let us find the median of the given data.

Solution:

Question 15. If the median of the following data is 32, let us determine the values of x and y when the sum of the frequencies is 100.

Solution:

32 = \(\ell+\left(\frac{\frac{n}{2}-c . f}{f}\right) \times h\)

32 = \(30+\frac{50-(35+x)}{30} \times 10\)

32 – 30 = \(\frac{50-35-x}{3}\)

or, 6 = 15 – x  ∴ x = 15 – 6 = 9

x + y = 25 ∴ y = 25 – 9 = 16

Application 1. Let us draw less than type Ogive and greater than type Ogive and let us find the median of the following frequency distribution table.

solution:

Assuming on graph paper along x-axis 1 small division 1 unit, & along y-axis 1 small division=1 unit, we draw greater than type Ogive & less than type Ogive. For greater than type Ogive plotting the points (50, 114), (55, 112), (60, 104), (65, 92), (70, 68), (75, 54), (80, 38).

And for less than type Ogive plotting the points (55, 2), (60, 10), (65, 18), (70, 30) (75, 54), (80, 88) & (85, 144) on graph paper, we join them.

The greater than type Ogive & less than type Ogive intersect each other at point P. Draw perpendicular PM on the x-axis from P which intersects. the x-axis at point M. 

The co-ordinates of M = (75, 0)

∴ Median = 75.

West Bengal Board Class 10 Math Book Solution In English Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.1

Application 1. The marks obtained by 30 students of the class of the Bishakha in Geography are :

60, 78, 80, 69, 73, 61, 82, 78, 79, 72, 78, 62, 80

71, 82, 73, 62, 80, 74, 78, 62, 80, 66, 70, 79, 75

Let us find the arithmetic mean of marks obtained in Geography. 

Solution: To find the Arithmetic mean of marks obtained in Geography

Read and Learn More WBBSE Solutions For Class 10 Maths

1. I have written the ages of my 40 friends in the table given below

Solution:

∴ Average age = \(\frac{\Sigma f_{x_i}}{\Sigma f_i}=\frac{697}{40}=17.425\)

2. I have written the number of members in each of the 50 families of our village in the table given below

Solution:

3. If the arithmetic mean of the data given below is 20.6, let us find the value of ‘a’.

Solution:

4. If the arithmetic mean of the distribution given below is 15, let us find the value of p.

Solution:

5. Rahamatchacha will go to the retail market for selling mangoes kept in 50 packing boxes. Let us write the number of boxes contained for varying numbers of mangoes in the table given below.

Solution:

6. Mohidul has written the ages of 100 patients of a village hospital. Let us write by calculating the average age of 100 patients.

Solution:

7. Let us find the mean of the following data by the direct method.

Solution:

Question 8. Let us find the mean of the following data by the assumed mean method.

1.

Solution:

2.

Solution:

Question 9. Let us find the mean of the following data by step deviation method.

1.

Solution: Let assumed mean a = 75

μ_i = x_i-a/h, h

= 30-0= 60-30

= 90-60

μ_i =30

2.

Solution: Let assumed mean a = 35

μ_i = x_i-a/h , h

= 14-0

= 28-14

= 42-28

μ_i = 14

Question 10. If the mean of the following frequency distribution table is 24, let us find the value of p.

Solution:

Here, mean = 24 (given)

∴ \(\frac{\Sigma \mathrm{f}_{\mathrm{i}_{\mathrm{i}}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\overline{\mathrm{x}}\)

⇒ \(\frac{1700+35 p}{80+p}=24\)

or, 1700 + 35p = 1920 + 24p

or, 35p – 24p = 1920 – 1700

or, 11p = 220

or, p = \(\frac{220}{11}\)

∴ p = 20

Question 11. Let us see the ages of the persons present in a meeting and determine their average age from the following table

Solution:

Question 12. Let us find the mean of the following data

Solution:

Question 13. Let us find the mean of marks obtained by girl students if their cumulative frequencies are as follows

Solution:

Question 14. Let us find the mean of the marks obtained from 60 students from the table given below.

Solution:

Application 1. The points obtained by two kabaddi teams in different matches are

given below. Let us determine their median.

1. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

2. 6, 7, 8, 8, 9, 10, 15, 15, 16, 17, 19, 25

Solution:

1. Find the median

5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

Here no. of terms(n) = 11 (i.e., odd)

∴ Median = (11+1/2)^th value = 6th value = 10

2. Find the median 

6, 7, 8, 8, 9, 10, 15, 15, 16, 17, 19, 25 

Here no. of terms (n) = 12 (i.e., even)

∴ Required median = 1/2{(12/2)^th value + ((12/2 + 1)^th value}

= 1/2(6th value + 7th value)

= 1/2(10+15)

= 25/2

Required median  = 12.5

Application 2. Let us find the median from the following distribution table.

Solution:

Application 3. Let us see the following frequency distribution table and let us find the median.

Solution:

∴ x = \(\Sigma \boldsymbol{\Sigma}=80\)

∴ \(\frac{x}{2}\) = 40

The corresponding class of cumulative frequency just greater than 40 is (20 – 30)

∴ Required median class is (20 – 30)

∴ Required median = \(\ell+\left[\frac{\frac{n}{2}-c . f}{f}\right] \times h\)

= \(20+\left[\frac{40-18}{24}\right] \times 10\)          Here l = 20, c.f = 18

= \(20+\frac{22}{24} \times 10\)

=  \(\frac{n}{2}\) = 40

= 20 + 9.16 = 29.16   f = 24, h = 20

∴ Median = 29.17 (approx)

Application 4. If the median of the following data is 28.5, and the total frequency is 100, let us find the values of x and y.

Solution:

⇒ \(28.5=20+\frac{30-(5+x)}{20} \times 10\)

⇒ \(20+\frac{30-5-x}{2}\)

⇒ \(28.5=\frac{40+30-5-x}{2}\)

57 = 65 – x

∴ x = 65 – 57 = 8

From (1), x + y = 15

∴ y = 15 – x = 15 – 8 = 7

∴ x = 8  and y = 7

Maths WBBSE Class 10 Solutions Chapter 25 Application Of Trigonometric Ratios Heights & Distances Exercise 25.1

Application 1. If the angle of elevation at the top of the coconut tree is 60° with respect to a point which is 20 metres away in the horizontal plane from the foot of the coconut tree, let us write by calculating the height of the coconut tree. 

Solution:

Given

If the angle of elevation at the top of the coconut tree is 60° with respect to a point which is 20 metres away in the horizontal plane from the foot of the coconut tree,

tan60° = AB/BC

or, √3 = AB/20

∴AB = 20 √3 m.

Read and Learn More WBBSE Solutions For Class 10 Maths

Application 2. Let us find what will be the angle of elevation of the sun when the length of the shadow of a stick of 20 metres will be 12√3 metres. 

Solution: tanC = AB/BC

= 20/ 20√3

= 1/√3

= tan 30°

∴ ∠C = 30°

Application 3. From a point at the top of a building of 60 metres height, it is observed that the angles of depression of the top and foot of the tower are 30° and 60° respectively. Let us write by calculating the height of the tower.

Solution:

In ΔABC, from a point at the top of a building of 60 metres height, it is observed that the angles of depression of the top and foot of the tower are 30° and 60° respectively.rom a point at the top of a building of 60 metres height, it is observed that the angles of depression of the top and foot of the tower are 30° and 60° respectively.

tan60° = \(\frac{AB}{BC}\)

∴ \(\sqrt{3}=\frac{60}{B C}\)

∴ \(B C=\frac{60}{\sqrt{3}}=\frac{60 \sqrt{3}}{3}\)

= 20 √3 m.

∴ DE = 20 √3

In △ADE, tan30° = \(\frac{AD}{DE}\)

⇒ \(\frac{1}{\sqrt{3}}=\frac{A D}{20 \sqrt{3}}\)

∴ √3  AD = 20√3

∴BC= DB = AB – AD

=60-20 = 40 m.

∴ Height of the building = 40 m

Question 4. If the angle of elevation of the top of a coconut tree from a point on the ground is 60° and the point is 20 metres away from the foot of the tree, let us find the height of the tree.

Solution:

If the angle of elevation of the top of a coconut tree from a point on the ground is 60° and the point is 20 metres away from the foot of the tree

AB = coconut tree

In ΔABC,

tan C = \(\frac{AB}{BC}\)

or, tan60° = \(\frac{AB}{20 m}\)

or, √3 = \(\frac{AB}{20 m}\)

∴ AB = 20 √3 m

∴ Height of the tree = 20 √3 m

 

Question 5. The length of the shadow of a tower is 9 metres when the sun’s angle of elevation is 30°. Let us write by calculating the height of the tower.

Solution:

The length of the shadow of a tower is 9 metres when the sun’s angle of elevation is 30°.

AB = Tower

BC = Length of shadow = 9 m

In ΔABC,

tan C = \(\frac{AB}{BC}\)

or, tan30° = \(\frac{AB}{9m}\)

or, \(\frac{1}{\sqrt{3}}=\frac{A B}{9 m}\)

∴ \(A B=\frac{9}{\sqrt{3}}=\frac{9 \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}}=\frac{9 \sqrt{3}}{3}=3 \sqrt{3} \mathrm{~m}\)

∴ Height of the tower = 3√3 m.

 

Question 6. A kite is flying with a thread of 150 metres long from a field. If the thread of the kite makes an angle of 60° with the horizontal line, let us write by calculating the height of the kite from the ground.

Solution:

A kite is flying with a thread of 150 metres long from a field. If the thread of the kite makes an angle of 60° with the horizontal line,

Here, let the height of Kite = AB

length of the thread = AC = 150m.

In ABC

sinC = \(\frac{AB}{AC}\)

or, \(\sin 60^{\circ}=\frac{A B}{A C}\)

or, \(\frac{\sqrt{3}}{2}=\frac{A B}{150}\)

or, 2 x AB = 150√3

∴ \(A B=\frac{150 \sqrt{3}}{2}=75 \sqrt{3} \mathrm{~m}\)

∴ Height of the Kite = 75√3  m.

Question 7. A palm tree stands on the bank of a river. A post is fixed in the earth on the other bank just opposite the palm tree. On moving 7 √3 metres from the post along the bank, it is found that the tree makes an angle of 60° at that point with respect to this bank. Let us find the width of the river.

Solution:

A palm tree stands on the bank of a river. A post is fixed in the earth on the other bank just opposite the palm tree. On moving 7 √3 metres from the post along the bank, it is found that the tree makes an angle of 60° at that point with respect to this bank.

Here AB is the width of the river

In △ABC,

tan C = \frac{AB}{BC}

or, \tan 60^{\circ}=\frac{A B}{7 \sqrt{3}}

∴ √3 = \frac{A B}{7 \sqrt{3}}

∴ AB = 7√3.√3 = 7 x 3 = 21 m

∴ Width of the river = 21m.

Question 8. A telegraph post is bent at a point above the ground due to a storm. Its top just meets the ground at a distance of 8 √3 metres from its foot and makes an angle of 30°. Let us write by calculating at what height the post is bent and what is the height of the post.

Solution:

The telegraph post is bent at a point above the ground due to a storm. Its top just meets the ground at a distance of 8 √3 metres from its foot and makes an angle of 30°.

Here PB is the height of the post which is bent at A & its top just meets the ground at C, at a distance of 8√√3 m from the foot of the post.

∴ PA = AC, ∠c = 30°

In △ABC,

tan C = \(\frac{AB}{BC}\)

or, tan30° = \(\frac{A B}{8 \sqrt{3}}\)

or, \(\frac{1}{\sqrt{3}}=\frac{A B}{8 \sqrt{3}}\)

∴ \(A B=\frac{8 \sqrt{3}}{\sqrt{3}}=8 \mathrm{~m}\)

Now, sin30° = \(\frac{AB}{AC}\)

or, \(\frac{1}{2}\) = \(\frac{8}{AC}\)

∴ AC = 8 x 2 = 16 m

∴ PA = AC = 16 m

Total height of the post = 16 + 8 = 24 m and the post bent at a height of 8m from the ground.

Question 9. Two houses stand just on opposite sides of the road of our village. A ladder that stands against the wall of the first house is at a distance of 6 metres from the house and makes an angle of 30° with the horizontal line. But if the ladder stands against the wall of the second housekeeping its foot at the same point, it makes an angle of 60° with the horizontal line.

1. Let us find the length of the ladder.

2. Let us write by calculating, the distance of the foot of the ladder from the foot of the wall of the second house.

3. Let us find the width of the road.

4. Let us find the height where the top of the ladder is fixed against the wall of the second house.

Solution:

Given

Two houses stand just on opposite sides of the road of our village. A ladder that stands against the wall of the first house is at a distance of 6 metres from the house and makes an angle of 30° with the horizontal line. But if the ladder stands against the wall of the second housekeeping its foot at the same point, it makes an angle of 60° with the horizontal line.

Here AB abd CD are two houses, on the opposite side of the road BD.

P is a point on the road, which is at a distance of 6 m from the foot of the 1st house AP is the length of the ladder.

Question 10. If the angle of elevation of the top of a chimney from a point on the horizontal plane passing through the foot of the chimney is 60° and the angle of elevation from another point on the same plane at a distance of 24 metres from the first point is 30°, let us write by calculating the height of the chimney. [Let us find the approximate value correct up to three decimal places, assuming √3 = 1.732 (approx)].

Solution:

If the angle of elevation of the top of a chimney from a point on the horizontal plane passing through the foot of the chimney is 60° and the angle of elevation from another point on the same plane at a distance of 24 metres from the first point is 30°

Let AB is the height of the chimney = h m

Question 11. The length of the shadow of a post becomes 3 metres smaller when the angle of elevation of the sun increases from 45° to 60°. Let us find the height of the post. [Let us find the approximate value correct up to three decimal places, assuming √3 = 1.732 (approx)].

Solution:

The length of the shadow of a post becomes 3 metres smaller when the angle of elevation of the sun increases from 45° to 60°

Let AB = height of the post = h m.

x√3 = x + 3

or, x√3 –  x = 3  or x(√3 – 1) = 3

∴ x=\frac{3}{\sqrt{3}-1}=\frac{3(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}

∴ x=\frac{3(\sqrt{3}+1)}{3-1}=\frac{3(\sqrt{3}+1)}{2}

∴ h=x+3=\frac{3(\sqrt{3}+1)}{2}+3=\frac{3 \sqrt{3}+3+6}{2}=\frac{9+3 \sqrt{3}}{2}

= \frac{9+3 \times 1.732}{2}=\frac{9+5.196}{2}=\frac{14.196}{2}=7.098 \mathrm{~m}

∴ Height of the post = 7.098 m.

Question 12. When the top of a chimney of a factory is seen from a point on the roof of the three-storied building of 9 √3 metres in height, the angle of elevation is 30°. If the distance between the factory and the chimney is 30 metres, let us write by calculating the height of the chimney.

Solution:

When the top of a chimney of a factory is seen from a point on the roof of the three-storied building of 9 √3 metres in height, the angle of elevation is 30°. If the distance between the factory and the chimney is 30 metres

Let AB = height of the chimney

Question 13. The bottom of a lighthouse and the bottom of the mast of two ships are on the same straight line and the angles of depression from the lighthouse at the bottom of the mast of the two ships are 60° and 30° respectively. If the distance between the points at the bottom of the lighthouse and the bottom of the mast of the first ship is 150 metres, let us write by calculating, how far will the mast of the other ship from the lighthouse and what the height of the lighthouse will be.

Solution:

The bottom of a lighthouse and the bottom of the mast of two ships are on the same straight line and the angles of depression from the lighthouse at the bottom of the mast of the two ships are 60° and 30° respectively. If the distance between the points at the bottom of the lighthouse and the bottom of the mast of the first ship is 150 metres,

Let AB is the height of lighthouse = h m

& C & D are the position of two ships.

In ΔABC,

tan60° = AB/BC

Question 14. From a point on the roof of a storied building, the angle of elevation of the top of a monument and that of the angle of depression of the foot of the monument are 60° and 30° respectively. If the height of the building is 16 metres, let us write by calculating the height of the monument and the distance of the building from the monument.

Solution:

From a point on the roof of five five-story buildings, the angle of elevation of the top of a monument and that of the angle of depression of the foot of the monument are 60° and 30° respectively. If the height of the building is 16 metres,

Let AB 16 m Height of the building

Question 15. I am flying a kite having a length of thread of 250 metres; when the thread makes an angle of 60° with the horizontal line, and when the thread makes an angle of 45° with the horizontal line. Let us write by calculating in each case what is the height of the kite from me. Let us find in which of the two cases will the kite be at a greater height from the other.

Solution:

I am flying a kite having a length of thread of 250 metres; when the thread makes an angle of 60° with the horizontal line, and when the thread makes an angle of 45° with the horizontal line.

In both cases A is the position of a Kite of different heights

AB = length of thread = 250 m (Both cases)

In 1st case, angle of elevation = 60°, & the height of Kite = AC

∴ In △ABC,

Sin60° = \(\frac{AC}{AB}\)

\(\frac{\sqrt{3}}{2}=\frac{A C}{250}\)

∴ \(A C=\frac{250 \sqrt{3}}{2}=125 \sqrt{3} \mathrm{~m}\)

In 2nd case, angle of elevation = 45° & the height of Kite = AC

 

Question 16. A passenger of an aeroplane observes that Howarh station is on one side of the plane and Saheed Minar is just on the opposite side. The angles of depression of Howrah station and Saheed Minar from the passenger of the aeroplane are 60° and 30° respectively. If the aeroplane is at a height of 545 √3 metres at that time, let us find the distance between Howrah station and Saheed Minar.

Solution:

A passenger of an aeroplane observes that Howarh station is on one side of the plane and Saheed Minar is just on the opposite side. The angles of depression of Howrah station and Saheed Minar from the passenger of the aeroplane are 60° and 30° respectively. If the aeroplane is at a height of 545 √3 metres at that time

Let the height of the plane AD = 545 √3 m.

Question 17. The length of the flag on the roof of the three-storied building is 3.3 metres. From any point of the road, the angle of elevation of the top of the second tower is 60°, let us write by calculating what is the angle of elevation of the top of the second tower from the foot of the first.

Solution:

The length of the flag on the roof of the three-storied building is 3.3 metres. From any point of the road, the angle of elevation of the top of the second tower is 60°,

Let BC is the height of the building = x m.

& AB The length of flag = 3.3 m

∠ADC = 50°; ∠BDC = 45°

Question 18. The heights of the two towers are 180 metres and 60 metres respectively. If the angle of elevation of the top of the first tower from the foot of the second tower is 60°, let us write by calculating what is the angle of elevation of the top of the second tower from the foot of the first.

Solution:

The heights of the two towers are 180 metres and 60 metres respectively. If the angle of elevation of the top of the first tower from the foot of the second tower is 60°,

Let CD and AB be two towers of heights 180 m & 60 m respectively. In ABCD,

Question 19. The length of the shadow of a tower standing on the ground is found to be 60 metres more when the sun’s angle of elevation changes from 30° to 60°, let us find the height of the chimney.

Solution:

The length of the shadow of a tower standing on the ground is found to be 60 metres more when the sun’s angle of elevation changes from 30° to 60

Let AB = height of the tower – hm.

In ΔABC,

Question 20. From a point on the same plane along the horizontal line passes through the foot of a chimney, the angle of elevation of the top of the chimney is 30° and the angle of elevation of the top of the chimney is 60° at a point on the same straight line proceeding 50 metres nearer to the chimney. Let us write by calculating the height of the chimney.

Solution:

From a point on the same plane along the horizontal line passes through the foot of a chimney, the angle of elevation of the top of the chimney is 30° and the angle of elevation of the top of the chimney is 60° at a point on the same straight line proceeding 50 metres nearer to the chimney.

Let the height of the chimney = be AB = h m.

x√3 =x+50/√3

or, 3x = x + 50

or, 2x = 50

∴ x = 25 m.

h=x√3 = 25√3 m.

∴ Height of chimney = 25√3 m.

Question 21. A vertical post of 126 dm height was bent at some point above the ground and it just touched the ground making an angle of 30° with the ground. Let us write by calculating at what height was the post bent and at what distance it met the ground from the foot of the post.

Solution:

A vertical post of 126 dm height was bent at some point above the ground and it just touched the ground making an angle of 30° with the ground.

Let AB Height of the post = 126 dm.

Question 22. Mohit, standing in the midst of a field, observes a flying bird in his north at an angle of elevation of 30° and after 2 minutes he observes the bird in his south at an angle of elevation of 60°. If the bird flies in a straight line all along at a height of 50√3 metres, let us find its speed in kilometres per hour.

Solution:

Mohit, standing in the midst of a field, observes a flying bird in his north at an angle of elevation of 30° and after 2 minutes he observes the bird in his south at an angle of elevation of 60°. If the bird flies in a straight line all along at a height of 50√3 metres,

Mohit standing at ‘C’ on the ground observes a bird in flying along AB from North to South at a height CD = 50√3 m above the ground.

Question 23. Amitadidi standing on a railway overbridge of 5√3 metres height observed the engine of the train from one side of the bridge at an angle of depression of 30°. But just after 2 seconds, she observed the engine at an angle of depression of 45° from the other side of the bridge. Let us find the speed of the train in metres per second. 

Solution:

Amitadidi standing on a railway overbridge of 5√3 metres height observed the engine of the train from one side of the bridge at an angle of depression of 30°. But just after 2 seconds, she observed the engine at an angle of depression of 45° from the other side of the bridge.

Let Amita Didi stand at A on the over bridge, which is at a height of 5√3 m from the ground. A train is moving from B to C.

Question 24. A bridge is situated at a right angle to the bank of the river. If one moves away a certain distance from the birdge along this side of the river, the other end of the bridge is seen at an angle of 45° and if someone moves a further distance of 400 metres in the same direction, the other end is seen at an angle of 30°. Let us find the length of the bridge.

Solution: Let AB = length of the bridge.

Question 25. A house is situated at a right angle to the bank of the river. If one moves away a certain distance from the bridge along this side of the river, the other end of the bridge is seen at an angle of 45° and if someone moves a further distance of 400 metres in the same direction, the other end is seen at an angle of 30°. Let us find the length of the chimney and the distance between the brick kiln and the house. 

Solution:

A house is situated at a right angle to the bank of the river. If one moves away a certain distance from the bridge along this side of the river, the other end of the bridge is seen at an angle of 45° and if someone moves a further distance of 400 metres in the same direction, the other end is seen at an angle of 30°.

Let AB & CD be the heights of the house & the chimney respectively. AB 15m, ED 15 m.

:. CD = CE+ED 

= (45+ 15) m 

= 60 m.

∴ The height of the chimney = 60 m & the distance between the brick kiln and the house = BD = 15.√3 m. Ans.

Question 26. If the angle of depression of two consecutive milestones on a road from an aeroplane is 60° and 30° respectively, let us find the height of the aeroplane,

1. when the two milestones stand on opposite sides of the aeroplane,

2. when the two milestones stand on the same side of the aeroplane.

Solution:

1. In 1st case A is the position of the plane & B & C are two consecutive milestones on the opposite side of the plane.

Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 Multiple Choice Question

Question 1. If the angle of elevation of the top of the mobile tower from a distance of 10 metres from its foot is 60°, then the height of the tower is

1. 10 metres
2. 10√3 metres
3. metres √3
4. 100 metres

Solution: tan60° = AB/BC

or, √3 = AB/10     ∴AB = 10√3 m.

Answer. 2. 10√3 metres

Question 2. In the diagram beside, the value is

1. 30°
2. 45°
3. 60°
4. 75°

Solution: tanθ = AB/BC

= 5/5√3

= tan30°

∴ 0 = 30°

Answer. 1. 30°

West Bengal Board Class 10 Math Book Solution In English

Question 3. At what angle an observer observes a box lying on the ground from the roof of the three-storied building so that the height of the building is equal to the distance of the box from the building?

1. 15°
2. 30°
3. 45°
4. 60°

Solution: tanθ = AB/BC

= 1 

= tan45°

∴ 0 = 45°

Answer. 3. 45°

Question 4. The height of the tower is 100 √3 metres. The angle of elevation at the top of a tower from a point at a distance of 100 metres of the foot of the tower is

1. 30°
2. 45°
3. 60°
4. None of these

Solution: tanθ = AB/BC

100√3m/100=

= √3

tanθ = tan60°

Answer. 3. 60°

Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 True Or False

1. In AABC, ZB = 90°, if ZAB = BC, then C = 60°.

False

2. PQ is the height of a building OR is the base, and the angle of depression from a point P at point R is ZSPR. So, ZSPR = <PRQ.

True

Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 Fill In The Blanks

1. If the sun’s angle of elevation increases from 30° to 60°, the length of the shadow of a post Decreases (decreases/increases)

2. If the angle of elevation of the sun is 45°, then the length of shadow and length of post is Equal.

3. If the angle of elevation of the sun is Greater than 45°, the length of the shadow of the tower will be less than the height of the tower.

 

Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 Short Answers

Question 1. If the angle of elevation of a kite is 60° and the length of the thread is 20√3 metres, let us calculate the height of the kite above the ground.

Solution.

If the angle of elevation of a kite is 60° and the length of the thread is 20√3 metres,

Let the height of the kite = be AB & length of the thread = be 20√3 m.

Question 2. AC is the hypotenuse with a length of 100 metres of a right-angled triangle ABC and if AB = 50 √3 metres, let us find the value of ZC.

Solution.

AC is the hypotenuse with a length of 100 metres of a right-angled triangle ABC and if AB = 50 √3 metres

AC hypotenuse = 100 m.

Question 3. A tree breaks due to a storm and its top touches the ground in such a manner that the distance from the top of the tree to the base of the tree and present height are equal. Let us calculate how much angle is made by the top of the tree with the base.

Solution.

A tree breaks due to a storm and its top touches the ground in such a manner that the distance from the top of the tree to the base of the tree and present height are equal.

AB is the height of the tree.

∴ tanθ = PB/BC = h/h = 1

∴ tanθ = 1 = tan45°

∴ 0 = 45°

Question 4. In the right-angled triangle ABC, B = 90°, D is such a point on AB that AB: BC: BD = √3:1:1, let us find the value of ∠ACD.

Solution.

In the right-angled triangle ABC, B = 90°, D is such a point on AB that AB: BC: BD = √3:1:1

AB: BC BD = √3:1:1

Question 5. If the ratio between the length of the shadow of a tower and the height of the tower is √3:1, let us find the angle of elevation of the sun.

Solution.

If the ratio between the length of the shadow of a tower and the height of the tower is √3:1,

Let BC: AB = √3:1

Class 10 WBBSE Math Solution In English Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1

 

Application: 1. We understand that ZBCA and CAB are complementary [complementary/supplementary] to each other.

Read and Learn More WBBSE Solutions For Class 10 Maths

Application 2. Let us find the value of sec 90°/cosec41°

Solution: sec 49°/cosec41°

= sec 49°/cos ec(90° 49°) 

= sec 49°/sec 49°
= 1

Application 3. Let us show that sin43° cos47° + cos43° sin47° = 1

Solution: sin43° cos47° + cos43° sin47°

=sin(90° 47°) cos47° + cos(90° 47°) sin47°

= cos47° cos47° + sin47° sin47°

= cos247° + sin247° 

= 1

∴ L.H.S. = R.H.S. Proved.

Question 3. If tan50° = P/q let us find the value of cos40°.

Solution: tan50° = p/q

AC² = AB² + BC²

= p² + q²

∴ AC = √ p² + q²

cos 40º = cos BAC = AB/AC = P/√ p² + q²

 

Question 4. 

1. sin 38º/cos 52º

Solution: sin 38º/cos 52º

= sin38º/cos(30 – 38)º

= sin38º/sin38

= 1

2. cosec 79º/sec11º

Solution: cosec 79º/sec11º

= cosec 79º/sec(90º-79º)

= cosec 79º/cosec 79º

= 1

3. tan27º/cot63º

Solution: tan27º/cot63º

= tan(90º-63º)/cot63º

= cot63º/cot63º

= 1

Question 5.

1. sin66º – cos24º = 0

Solution: L.H.S = sin66º – cos24º

= sin(90º – 24º)

= cos 24º – cos 24º

= 0

= R.H.S

2. cos²57º + cos²33º = 1

Solution: cos²57º + cos²33º

= cos²(90º – 30º) + cos²33º

= sin²33º + cos²33º

= 1

= R.H.S

3. cos²75º-sin²12º = 0

Solution: L.H.S = cos²75º-sin²12º

= cos²(90º-15º) – sin²15º

= sin²15º – sin²15º

= 1

= R.H.S

4. cosec²48º – tan²42º = 1

Solution: L.H.S = cosec²48º – tan²42º

= cosec²48º – tan²(90º-48º)

= cosec²48º – cot²48º

= 1

= R.H.S

Class 10 WBBSE Math Solution In English

5. sec 70ºsin20º + cos20º cosec70º = 2

Solution: L.H.S = sec 70ºsin20º + cos20º cosec70º

= sec(90º – 20º) sin20º + cos20º. cosec(90º-20º)

= cosec20º . sin20º + cos20º x 1/cos20º

= 1+1

= 2

= R.H.S

Question 6. If two angles a and ẞ are complementary angles, let us show that:

1. sin’α + sin2ß = 1

Solution: L.H.S. = sin2α + sin2ß

= sin2(90-B) + sin2ß          [As α + B = 90°]

=cos2B+ sin2B

= 1

= R.H.S.

2. cotẞ + cosẞ= cosẞ/cosα(1 + sinẞ)

Solution: R.H.S = cosẞ/cosα(1 + sinẞ)

= \(\frac{\cos \beta}{\cos (90-\beta)}(1+\sin \beta)\)

= \(\frac{\cos \beta}{\sin \beta}(1+\sin \beta)\)

= \(\frac{\cos \beta}{\sin \beta} \times 1+\frac{\cos \beta}{\sin \beta} \times \sin \beta\)

= \(\cot \beta+\cos \beta=\text { L.H.S. }\)

3. secα/cosα – cot²β =1

Solution: L.H.S = secα/cosα – cot²β

= sec²α – cot²α(90º-α)

= sec²α – tan²α

= 1

= R.H.S

4. If sin 17° = x/y, let us show that sec17° – sin73° = x²/y√y²-x²

Solution: sin17º = x/y

∴ \(B C^2=A C^2-A B^2\)

= \(y^2-x^2\)

∴ \(B C=\sqrt{y^2-x^2}\)

L.H.S. = sec17º – sin73º

= \(\frac{A C}{B C}-\frac{B C}{A C}\)

= \(\frac{y}{\sqrt{y^2-x^2}}-\frac{\sqrt{y^2-x^2}}{y}\)

= \(\frac{y^2-\left(y^2-x^2\right)}{y\left(\sqrt{y^2-x^2}\right)}=\frac{x^2}{y \sqrt{y^2-x^2}}=\text { R.H.S. }\)

5. Let us show that sec²12° – 1/tan278°

Solution: L.H.S. = sec²12°

= \(\sec ^2 12^{\circ}-\frac{1}{\tan ^2\left(90^{\circ}-12^{\circ}\right)}=\sec ^2 12^{\circ}-\frac{1}{\cot ^2 12^{\circ}}\)

= \(\sec ^2 12^{\circ}-\tan ^2 12^{\circ}=1=\text { R.H.S }\)

6. ∠A + ∠B = 90°, let us know that 1+tanA/tanB = sec²A

Solution: ∠A + ∠B = 90°

∠B = 90° – ∠A

tan∠B = tan(90° – A)

= cot ∠A

L.H.S = \(1+\frac{\tan A}{\tan B}\)

= \(1+\frac{\tan A}{\cot A}=1+\tan A \times \tan A\)

= \(1+\tan ^2 A=\sec ^2 A=\text { R.H.S. }\)

7. Let us show that cosec²22°cot²68° = sin²22°+sin²68°+cot²68°

Solution: L.H.S = cosec²22°cot²68°

= \({cosec}^2\left(90^{\circ}-68^{\circ}\right) \cot ^2 68^{\circ}\)

= \(\sec ^2 68^{\circ} \cdot \cot ^2 68^{\circ}\)

= \(\frac{1}{\cos ^2 68^{\circ}} \times \frac{\cos ^2 68^{\circ}}{\sin ^2 68^{\circ}}\)

= \(\frac{1}{\sin ^2 68^{\circ}}={cosec} 268^{\circ}\)

R.H.S = \(\sin ^2 22^{\circ}+\sin ^2 68^{\circ}+\cot ^2 68^{\circ}\)

= \(\sin ^2\left(90^{\circ}-68^{\circ}\right)+\sin ^2 68^{\circ}+\cot ^2 68^{\circ}\)

= \(\cos ^2 68^{\circ}+\sin ^2 68^{\circ}+\cot ^2 68^{\circ}\)

= \(1+\cot ^2 68^{\circ}\)

= \({cosec}^2 68^{\circ}\)

∴ L.H.S = R.H.S

8. If ∠P + ∠Q = 90º, let us show that, √sinP/cosQ – sinPcosQ = cosP

Solution: L.H.S = √sinP/cosQ – sinPcosQ         P+Q = 90º , Q =90º-P

= \(\sqrt{\frac{\sin P}{\sin P}-\sin P \cdot \sin P}\)

= \(\sqrt{1-\sin ^2 P}\)

= \(\sqrt{\cos ^2 P}\)

= cosP = R.H.S

9. Let us prove that cot12ºcot38ºcot52ºcot78ºcot60º = 1/√3

Solution: L.H.S = cot12ºcot38ºcot52ºcot78ºcot60º

= \(\cot \left(90^{\circ}-78^{\circ}\right) \cot 38^{\circ} \cot \left(90^{\circ}-38^{\circ}\right) \cot 78^{\circ} \times \frac{1}{\sqrt{3}}\)

= \(\tan 78^{\circ} \cdot \cot 38^{\circ} \cdot \tan 38^{\circ} \cot 78^{\circ} \times \frac{1}{\sqrt{3}}\)

= \(\tan 78^{\circ} \cdot \cot 78^{\circ} \cdot \cot 38^{\circ} \cdot \tan 38^{\circ} \cdot \frac{1}{\sqrt{3}}\)

= \(1 \times 1 \times \frac{1}{\sqrt{3}}\)

= \(\frac{1}{\sqrt{3}}\) = R H S

Question 7. AOB is the diameter of a circle with center O and C is any point on the circle, joining A, C; B, C; O, C, let us show that ZACB = semicircle angle = 90°

1. tan ∠ABC = cot ∠ACO

Solution:

AOB is a diameter of a circle with center O and C is any point on the circle, joining A, C; B, C; O, C,

L.H.S. = tan ∠ABC

= tan(90° ∠ACO)

= cot∠ACO

= R.H.S       [As OB = OC]

2. sin² ∠BCO + sin² ∠ACO = 1

Solution: L.H.S= sin² ∠BCO + sin² ∠ACO

= sin²(90° -∠ACO) + sin² ∠ACO

= cos²∠ACO + sin² ∠ACO

= 1. R.H.S.

3. cosec2 CAB – 1 = tan2 ZABC 

Solution: L.H.S. cosec²∠CAB-1

= cosec²(90° – ∠ABC) – 1

= sec² ∠ABC – 1 

= tan² ∠ABC

= R.H.S.

Question 8. ABCD is a rectangular figure joining A, and C let us prove that:

1. tan ∠ACD = cot ∠ACB

Solution: tan ∠ACD tan(90° – ∠ACB)

= cot∠ACB= R.H.S

2. tan²∠CAD + 1 = 1/sin²∠BAC

Solution: tan²∠CAD + 11

= tan²(90° – <BAC) + 1

= cot²∠BAC +1

= cosec² ∠BAC

=1/sin²∠BAC

= R.H.S.

WBBSE Solutions Guide Class 10 Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 Multiple Choice Question

Question 1. The value of (sin43° cos47° + cos43° sin47°) is

1. 0
2. 1
3. sin4°
4. cos4°

Solution: sin43° cos47° + cos43° sin47°

= cos47°. cos47° + sin47°. sin47°

= cos247° + sin247°

= 1

Answer. 2. 1

Question 2. The value of  tan35°/cot55° +  cot78°/tan12°

1. 0
2. 1
3. 2
4. None of this

Solution : tan35°/cot55° +  cot78°/tan12°

= tan 35°/cot(90-35°) + cot 78°/ tan(90°-78°)

= tan 35° /tan 35° + cot 78°/cot 78°

=1+1

=2

Answer. 3. 2

Question 3. The value of {cos(40° +8) sin(50° – 0)} is

1. 2cosθ
2. 7sinθ
3. 0
4. 1

Solution: cos(40 + θ) – sin(50 – θ)

= cos(40+θ) cos(90 (50-θ)}

= cos(40+θ) cos(40 + θ)

= 0

Answer: 3. 0

Question 4. ABC is a triangle. sin(B+C/2)

1. sin A/2
2. Cos A/2
3. sin A
4. cosA

Solution: A/2 + B/2 + C/2 = 90º

∴ \(\frac{B}{2}+\frac{C}{2}=90^{\circ}-\frac{A}{2}\)

∴ \(\sin \left(\frac{B+C}{2}\right)=\sin \left(90^{\circ}-\frac{A}{2}\right)\)

= \(\cos \frac{A}{2}\)

Question 5. if A+B = 90º and tan A = 3/4, value of cot B is.

1. 3/4
2. 4/3
3. 3/5
4. 4/5

Solution: cot B = cot(90º – A) = tanA = 3/4

Answer: 1. 3/4

Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 True Or False

Question 1. The values cos54° and sin36° are equal.

True

Question 2. The simplified value of (sin12° – cos78°) is 1

False

WBBSE Class 10 Maths Solutions Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 Fill In The Blanks

1. The value of (tan15° x tan45° x tan60° x tan78°) is √3.

2. The value of (sin12° x cos18° x sec78° x cosec72°) is 1.

3. If A and B are complementary to each other, sin A = cos B.

WBBSE Class 10 Maths Solutions Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 Short Answer

Question 1. If sin 10θ cos8θand 100 is a positive acute angle, let us find the value of tan 9θ.

Solution.

If sin 10θ cos8θand 100 is a positive acute angle

sin10θ = cos8θ

or, sin10θ = sin(90° – 8θ)

or, 10θ = 90°-8θ

18θ = 90°      θ = 90/18 = 5°

= tan9θ

= tan(9 x 5°) 

= tan45° 

= 1

Question 2. If tan4θ x tan60 = 1 and 60 is a positive acute angle, let us find the value of θ. 

Solution.

If tan4θ x tan60 = 1 and 60 is a positive acute angle

tan4θ x tan6θ = 1

or, tan4θ = 1/tan 6θ

cot6θ = tan(9θ-6θ)

∴ 4θ = 90-6θ

or, 10θ = 90   

 ∴ 0 = 90/10

= 9°

Question 3. Let us find the value of 2sin²63°+1+2sin²27°/ 3cos²17° -2+3cos² 73°

Solution: 2sin²63°+1+2sin²27°/ 3cos²17° -2+3cos² 73°

= \(\frac{2 \sin ^2 63^{\circ}+1+2 \sin ^2 27^{\circ}}{3 \cos ^2 17^{\circ}-2+3 \cos ^2 73^{\circ}}\)

= \(\frac{1+2\left(\sin ^2 63^{\circ}+\sin ^2 27^{\circ}\right)}{3\left(\cos ^2 17^{\circ}+\cos ^2 73^{\circ}\right)-2}=\frac{1+2 \times 1}{3 \times 1-2}=\frac{3}{1}=3\)

Question 4. Let us find the value of (tan1° x tan2° x tan3°———-tan89°).

Solution: tan1º x tan89º x tan2º x tan88º

= 1 x 1 x 1

= 1

Question 5. If sec5A = cosec (A + 36°) and 5A is a positive acute angle, let us find the value of A.

Solution.

If sec5A = cosec (A + 36°) and 5A is a positive acute angle

sec5A = cosec(A + 36)

= cosec(90° 5A) = cosec(A + 36°)

or, 90° – 5A = A + 36°

or, 90° – 36° 5A + A

or, 6A = 54°

A = 9°.

WBBSE Class 10 Maths Solutions Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3

Question 1. If sinθ = then let us write the value of cosec/1+cotθ by determining it.

Solution : sinθ =4/5

∴ cosecθ =1/sinθ

=5/4

cot²θ = cosec²θ – 1 = (5/4)²-1

= 25/16-1

= 25-16 / 16

= 9/16

∴ cosθ= √9/16

= 3/4

Now, cosecθ / 1+cotθ = 5/4 / 1+3/4

= 5/4 x 4/7

= 5/7

Read and Learn More WBBSE Solutions For Class 10 Maths

Question 2. If tanθ = 3/4, then let us show that √(1-sinθ/1+sinθ) = 1/2

Solution: tanθ = 3/4

let AB =3K

& BC = 4K

∴ AC² = AB²+BC²

= (3K)²+(4K)² = 9K²+16K²

= 25K²

.. AC = √25K²

= 5K

∴ sinθ = AB/AC = 3K/5K = 3/5

Now L.H.S = \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sqrt{\frac{1-3 / 5}{1+3 / 5}}=\sqrt{\frac{\frac{5-3}{5}}{\frac{5+3}{5}}}=\sqrt{\frac{2}{8}}=\sqrt{\frac{1}{4}}\)

= 1/2 = R.H.S Proved

Question 3. If tanθ = 1, then let us determine the value of 8sinθ+5cosθ/sin³ θ-2cos³θ+7 cosθ

Solution: tanθ = 1

We know, \(\tan \theta=\frac{P}{B}=\frac{A B}{B C}\)

∴ \(\mathrm{AC}^2=\mathrm{AB}^2+\mathrm{BC}^2\)

= \((1 K)^2+(1 K)^2=K^2+K^2=2 K^2\)

∴ \(\mathrm{AC}^2=\mathrm{AB}^2+\mathrm{BC}^2\)

= \((1 K)^2+(1 K)^2=K^2+K^2=2 K^2\)

∴ \(A C=\sqrt{2 K^2}=K \sqrt{2}\)

∴ \(\sin \theta=\frac{P}{H}=\frac{A B}{A C}=\frac{1 K}{\sqrt{2} K}=\frac{1}{\sqrt{2}}\)

& \(\cos \theta=\frac{B}{H}=\frac{B C}{A C}=\frac{1 K}{\sqrt{2} K}=\frac{1}{\sqrt{2}}\)

Now, \(\frac{8 \sin \theta+5 \cos \theta}{\sin ^3 \theta-2 \cos ^3 \theta+7 \cos \theta}\)

= \(\frac{8 \times \frac{1}{\sqrt{2}}+5 \times \frac{1}{\sqrt{2}}}{\left(\frac{1}{\sqrt{2}}\right)^3-2\left(\frac{1}{\sqrt{2}}\right)^3+7 \cdot \frac{1}{\sqrt{2}}}=\frac{\frac{8}{\sqrt{2}}+\frac{5}{\sqrt{2}}}{\frac{1}{2 \sqrt{2}}-2 \frac{1}{2 \sqrt{2}}+\frac{7}{\sqrt{2}}}=\frac{\frac{13}{\sqrt{2}}}{\frac{1-2+14}{2 \sqrt{2}}}\)

= \(\frac{13 / \sqrt{2}}{13 / 2 \sqrt{2}}=\frac{13}{\sqrt{2}} \times \frac{2 \sqrt{2}}{13}=2\)

Question 2.

1. Let us express cosecθ and tanθ in terms of sine.

Solution: cosecθ= 1/sinθ

tanθ= sin/cos

= sinθ/√1-sin²θ

2. Let us write cosecθ and tanθ in terms of cosθ

Solution: cosecθ =1/sinθ = 1/√1-cos²θ

tanθ = sinθ/cosθ

= √1-cos²θ/cosθ

Question 3.

1. If secθ + tanθ = 2, then let us determine the value of (secθ– tanθ). 

Solution: We know, sec²θ tan²θ = 1

or, (secθ+tanθ) (secθ-tanθ) = 1

or, 2 x (secθ – tanθ) = 1

secθ – tanθ = 1/2

2. If cosecê – cote = √2-1, then let us write by calculating, the value of (cosecθ + cotθ).

Solution: We know, cosec²θ – cot²θ

or, (cosecθ+cotθ) (cosecθ- cotθ) = 1

or, (cosecθ+cotθ) (√2+1) = 1

∴ cosecθ+cotθ = 1/√2-1 

= (√2+1)/(√2-1)(√2+1) 

= (√2+1)/2-1 = √2+1 

3. If sinθ+cosθ = 1, then let us determine the value of sine x cosθ. 

Solution: sinθ + cosθ = 1

or, (sinθ+cosθ)² = 12

or, sin²θ+ cos²θ + 2sinθ x cosθ = 1

or, 1+2sinθ cosθ = 1          [as sin²θ + cos²θ = 1]

∴ 2sinθ cosθ = 0                => sinθ cosθ = 0.

West Bengal Board Class 10 Math Book Solution In English

4. If tanθ+cotθ = 1, then let us determine the value of (tanθ – cotθ). 

Solution: (tanθ-cotθ)²= (tanθ + cotθ) – 4. tanθ . cotθ

=(2)² – 4 x tanθ x 1/tan θ

=4-4=0.

∴tanθ – cotθ = 0

5. If sinθ – cosθ = 7/13 then let us determine the value of sinθ + cosθ.

Solution: (sinθ cosθ)² = (7/13)²

or, sin²θ+ cos²θ – 2sinθ cosθ = 49/169

or, 1 – 2sinθ cosθ = 49/169

or, 1-169 = 2sinθ cosθ

or, 169-49/169 = 2sinθ cosθ

or,  120/169 = 2sinθ cosθ

∴ (sine+cose)²= sin²θ+ cos²θ + 2sinθ cosθ

= 1 + 120/169

= 120+169/169

= 289/169

∴ sinθ+cosθ = √289/169

=17/13

6. If sinθcosθ = 1/2, then let us write by calculating, the value of (sinθ + cosθ).

Solution: (sinθ+cosθ)²= sin²θ+ cosθ²+2. sinθ. cosθ

= 1+2×1/2 =2.

∴ sinθ cosθ = √2.

7. If sin θ + cos θ/ sin θ-cos θ =7, then let us write by calculating, the value of tanθ.

Solution: sin θ + cos θ / sinθ-cos θ =7

or, \(\frac{\sin \theta+\cos \theta+\sin \theta-\cos \theta}{\sin \theta+\cos \theta-\sin \theta+\cos \theta}=\frac{7+1}{7-1}\)

or, \(\frac{2 \sin \theta}{2 \sin \theta}=\frac{8}{6}\)

or, \(\tan \theta=\frac{4}{3}\)

8.  If secθ+cosθ = 5/3 then let us write by calculating, the value of (secθ – cosθ).

Solution: (secθ – cosθ)²= (secθ+cosθ)² – 4. secθ. cosθ

= (5/3)²- 4 . sec x 1/secθ

= 25/9 – 4

= 25- 1 / 9

9. Let us determine the value of tan from the relation 5sin²0 + 4cos²0 = 9/2

Solution: 5sin²θ + 4cos²θ = 9/2

\(\text { 5. } \sin ^2 \theta+4\left(1-\sin ^2 \theta\right)=\frac{9}{2}\) \(5 \sin ^2 \theta-4 \sin ^2 \theta+4=\frac{9}{2}\) \(\sin ^2 \theta=\frac{9}{2}-4=\frac{9-8}{2}=\frac{1}{2}\)

∴ \(\cos ^2 \theta=1-\sin ^2 \theta=1-\frac{1}{2}=\frac{1}{2}\)

∴  \(\tan ^2 \theta=\frac{\sin ^2 \theta}{\cos ^2 \theta}=\frac{1 / 2}{1 / 2}=1\)

∴ \(\tan \theta=\sqrt{1}=1\)

10. If sec²θ + tan²θ =13/12 then let us write by calculating, the value of (sec10 – tan10).

Solution: sec⁴θ– tan⁴θ

= (secθ+tan²θ) (sec²θ – tan²θ)

= 13/12 x 1

= 13/12

Question 4.

1. In ΔPQR, ∠Q is a right angle. If PR = √5 units and PQ – RQ = 1 unit, then let us determine the value of cos P – cos R.

Solution:

Given

In ΔPQR, ∠Q is a right angle. If PR = √5 units and PQ – RQ = 1 unit

cos P – cos R (given PQ – QR = 1)

= PQ/PR –  QR/PR 

= PQ-QR / PR 

= 1√5 unit

2. In ΔXYZ, Y is a right angle. If XY = 2√3 units and XZ – YZ = 2 units then let us determine the value of (sec X – tan X).

Solution: Given

In ΔXYZ, Y is a right angle. If XY = 2√3 units and XZ – YZ = 2 units

XY = 2√3 unit

& XZ – YZ = 2 units.

sec x – tan x

= \(\frac{X Z}{X Y}-\frac{Y Z}{X Y}\)

= \(\frac{X Z-Y Z}{X Y}=\frac{2}{2 \sqrt{3}}\)

∴ \(\sec X-\tan X=\frac{1}{\sqrt{3}}\)

Question 5. Let us eliminate ‘θ’ from the relations’

1. x = 2 sinθ, y = 3 cosθ

Solution: x = 2sinθ & y = 3coseθ

∴ sinθ = x/2          ∴ cosθ = y/3

We know, sin²θ + cos²θ = 1

∴ x²/4 + y2/9 = 1

2. 5x=3secθ, y = 3tanθ

Solution : 5x = 3 secθ;    &y = 3tanθ

∴ \(\sec \theta=\frac{5 x}{3}\)

∴ \(\tan \theta=\frac{y}{3}\)

We know, \(\sec ^2 \theta-\tan ^2 \theta=1\)

or, \(\left(\frac{5 x}{3}\right)^2-\left(\frac{y}{3}\right)^2=1\)

or, \(\frac{25 x^2}{9}-\frac{y^2}{9}=1\)

or, \(25 x^2-y^2=9\)

Question 6.

1. If sinα = 5/13 then let us show that, tanα+ secα = 1.5.

Solution: sinα = 5/13

Let PQ = 5k

PR = 13k

∴ QR = \(\sqrt{P R^2-P Q^2}\)

= \(\sqrt{(13 K)^2-(5 K)^2}\)

= \(\sqrt{169 K^2-25 K^2}=\sqrt{144 K^2}\)

∴ QR = 12k

∴ \(\tan \alpha+\sec \alpha=\frac{P}{B}+\frac{H}{B}=\frac{5 K}{12 K}+\frac{13 K}{12 K}=\frac{18 K}{12 K}=\frac{3}{2}=1.5\) Proved.

2. If tanA = n/m then let us determine the values of both sinA and secA.

Solution: tanA = n/m

or, \(\frac{\sin A}{\cos A}=\frac{n}{m}\)

⇒ \(\frac{\sin A}{\sqrt{1-\sin ^2 A}}=\frac{n}{m}\)

or, \(\frac{\sin ^2 A}{1-\sin ^2 A}=\frac{n^2}{m^2}\)

or, \(\frac{1-\sin ^2 A}{\sin ^2 A}=\frac{m^2}{n^2}\)

or, \(\frac{1}{\sin ^2 A}-\frac{\sin ^2 A}{\sin ^2 A}=\frac{m^2}{n^2}\)

or, \(\frac{1}{\sin ^2 A}-1=\frac{m^2}{n^2}\)

or, \(\frac{1}{\sin ^2 A}=\frac{m^2}{n^2}+1\)

or, \(\frac{1}{\sin ^2 A}=\frac{m^2+n^2}{n^2}\)

or, \(\sin ^2 A=\frac{n^2}{m^2+n^2}\)

∴ \(\sin A=\frac{n}{\sqrt{m^2+n^2}}\)

Again, \(\sec ^2 A-\tan ^2 A=1\)

or, \(\sec ^2 \mathrm{~A}=1+\tan ^{26} \mathrm{~A}\)

= \(1+\frac{n^2}{m^2}\)

= \(\frac{m^2+n^2}{m^2}\)

∴ \(\sec A=\sqrt{\frac{m^2+n^2}{m^2}}\)

3. If sec = x/√x² + y² then let us show that, x sinθ = y cosθ.

Solution:

⇒ \(\sin \theta=\sqrt{1-\cos ^2 \theta}=\sqrt{1-\left(\frac{x}{\sqrt{x^2+y^2}}\right)^2}\)

⇒ \(\sin \theta=\sqrt{1-\frac{x^2}{x^2+y^2}}=\sqrt{\frac{x^2+y^2-x^2}{x^2+y^2}}=\sqrt{\frac{y^2}{x^2+y^2}}=\frac{y}{\sqrt{x^2+y^2}}\)

∴ L.H.S. = x sinθ = \(x \cdot \frac{y}{\sqrt{x^2+y^2}}=\frac{x y}{\sqrt{x^2+y^2}}\)

R.H.S. = y cosθ = \(y \cdot \frac{x}{\sqrt{x^2+y^2}}=\frac{x y}{\sqrt{x^2+y^2}}\)

∴ L.H.S. = R.H.S.  Proved.

4. If sinα = a²-b² / a²+b² then let us show that, cotα = 2ab/a²-b²

Solution: sinα = a²-b² / a²+b²

∴ \(\cos ^2 \alpha=1-\sin ^2 \alpha=1-\frac{\left(a^2-b^2\right)}{\left(a^2+b^2\right)}=\frac{\left(a^2+b^2\right)-\left(a^2-b^2\right)}{\left(a^2+b^2\right)^2}\)

= \(\frac{\left(a^4+b^4+2 a^2 b^2\right)-\left(a^4+b^4-2 a^2 b^2\right)}{\left(a^2+b^2\right)^2}=\frac{4 a^2 b^2}{\left(a^2+b^2\right)^2}\)

∴ \(\cos \alpha=\frac{2 a b}{a^2+b^2}\)

⇒ \(\cot =\frac{\cos \alpha}{\sin \alpha}=\frac{2 a b /\left(a^2+b^2\right)}{\left(a^2-b^2\right) /\left(a^2+b^2\right)}\)

= \(\frac{2 a b}{\left(a^2+b^2\right)} \times \frac{\left(a^2+b^2\right)}{\left(a^2-b^2\right)}\)

∴ \(\cos \alpha=\frac{2 a b}{a^2-b^2}\) Proved.

5. If sinθ / x = cosθ / y then let us show that sinθ = x-y/√x² + y²·

Solution: sinθ / x = cos θ/ y = K(let)

∴ sinθ = xK & cosθ = yK

We know, \(\sin ^2 \theta+\cos ^2 \theta=1\)

or, \(\mathrm{x}^2 \mathrm{~K}^2+\mathrm{y}^2 \mathrm{~K}^2=1\)

or, \(\mathrm{K}^2\left(\mathrm{x}^2+\mathrm{y}^2\right)=1\)

∴ \(K^2=\frac{1}{x^2+y^2}\)

∴ \(K=\frac{1}{\sqrt{x^2+y^2}}\)

Now, sinθ – cosθ = xK – yK

= \(x \frac{1}{\sqrt{x^2+y^2}}-y \cdot \frac{1}{\sqrt{x^2+y^2}}\)

∴ \(\sin \theta-\cos \theta=\frac{x-y}{\sqrt{x^2+y^2}}\)  Proved.

6. If (1 + 4x²) cosA = 4x, then let us show that cosecA + cotA = 1+2x/1-2x

Solution: (1+ 4x²)cosA = 4x

∴ \(\cos A=\frac{4 x}{1+4 x^2}\)

⇒ \(\sin ^2 A=1-\cos ^2 A=1-\left(\frac{4 x}{1+4 x^2}\right)^2=\frac{\left(1+4 x^2\right)^2-16 x^2}{\left(1+4 x^2\right)^2}\)

= \(\frac{1+16 x^4+8 x^2-16 x^2}{\left(1+4 x^2\right)^2}=\frac{1+16 x^4-8 x^2}{\left(1+4 x^2\right)^2}=\frac{\left(1-4 x^2\right)^2}{\left(1+4 x^2\right)^2}\)

∴ \(\sin A=\frac{1-4 x^2}{1+4 x^2}\)

∴ \({cosec} A=\frac{1+4 x^2}{1-4 x^2}\)

⇒ \(\cot A=\frac{\cos A}{\sin A}=\frac{4 x / 1+4 x^2}{\left(1-4 x^2\right) / 1+4 x^2}=\frac{4 x}{1-4 x^2}\)

⇒ \({cosec} A+\cot A=\frac{1+4 x^2}{1-4 x^2}+\frac{4 x}{1-4 x^2}\)

= \(\frac{1+4 x^2+4 x}{1-4 x^2}=\frac{(1+2 x)^2}{(1+2 x)(1-2 x)}\)

∴ \({cosec} A+\cot A=\frac{1+2 x}{1-2 x}\)

Proved.

7. If x = a sine and y = b tanθ, then let us prove that a²/x²- b²/y² = 1

Solution: x = a sine & y = b tane

or, \(\sin \theta=\frac{x}{a}\)      ∴ \(\tan \theta=\frac{\mathrm{y}}{\mathrm{b}}\)

or, \({cosec} \theta=\frac{a}{x}\)   ∴ \(\cot \theta=\frac{b}{y}\)

We know, \({cosec}^2 \theta-\cot ^2 \theta=1\)

or, \(\frac{a^2}{x^2}-\frac{b^2}{y^2}=1\) Proved.

8. If sinθ + sin² = 1, then let us prove that cos²θ+ cos²θ = 1. 

Solution: sinθ + sin²θ = 1

∴ sinθ = 1 – sin²θ = cos²θ

∴ sin²θ = cos1θ

∴ cos²θ+ cos θ sine + sin²θ = 1 Proved

West Bengal Board Class 10 Math Book Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 Multiple Choice Question

1. If 3x = cosecα and 3/x = cot α ,then the value of 3(x² – 1/x²) is

1. 1/27
2. 1/81
3. 1/3
4. 1/9

Solution:  cosecα = 3x  & cot = 3/x

⇒ \({cosec}^2 \alpha-\cot ^2 \alpha=1\)

⇒ \((3 x)^2-\left(\frac{3}{x}\right)^2=1\)

or, \(9 x^2-\frac{9}{x^2}=1\)

or, \(3\left(3 x^2-\frac{3}{x^2}\right)=1\)

∴ 3x² – 3/x²

= 1/3

Answer: 3. 1/3

2. If 2x = sec A and 2/x = tan A, then the value of 2(x² – 1/x²)is

1. 1/2
2. 1/4
3. 1/8
4. 1/16

Solution: sec²A – tan²A= 1

or, \((2 x)^2-\left(\frac{2}{x}\right)^2=1\)

or, \(4 x^2-\frac{4}{x^2}=1\)

or, \(4\left(x^2-\frac{1}{x^2}\right)^2=1\)

⇒ \(2\left(x^2-\frac{1}{x^2}\right)^2=\frac{1}{2}\)

Answer: 1. 1/2

3. If tan∝ + cot ∝ = 2, then the value of (tan¹³∝ + cot¹³∝) is

1. 1
2. 0
3. 2
4. None

Solution: tan∝ + cot∝ = 2

or, \(\tan \alpha+\frac{1}{\tan \alpha}=2\)

⇒ \(\frac{\tan ^2 \alpha+1}{\tan \alpha}=2\)

or, \(\tan ^2 \alpha+1=2 \tan \alpha\)

or, \(\tan ^2 \alpha-2 \tan \alpha+1=0\)

⇒ \((\tan \alpha-1)^2=0\)

∴ tanα = 1 & cotα = 1

∴ \(\tan ^{13} \alpha+\cot ^{13} \alpha\)

= \((\tan \alpha)^{13}+(\cot \alpha)^{13}\)

= 1 + 1 = 2

Answer: 3. 2

4. If sin 0 – cos 0 = 0 (0º ≤θ≤ 90º) and sec θ + cosec θ = x, then the value of x is

1. 1
2. 2
3. √2
4. 2√2

Solution: sinθ- cosθ = 0

sinθ = cosθ

= sinθ (90 – θ)

∴ θ = 90° – θ

∴ 2 = 90°

∴ θ = 45°

secθ- cosecθ = x

or, sec45° + cosec45° = x

or, √2 + √2 = x

∴ 2√2 = x

∴ x = 2√2

Answer: 4. 2√2

5. If 2cos³θ = 1, then the value of θ is

1. 10º
2. 15º
3. 20º
4. 30º

Solution: 2cos³θ = 1

∴ cos3θ = 1/2 = cos60º

∴ 3θ = 60º           .. θ= 60º /2 = 20º

Answer: 3. 20º

West Bengal Board Class 10 Math Book Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 True Or False

1. If 0°< a < 90°, then the least value of (sec²α + cos²α) is 2.

Answer: True

2. The value of (cos0° x cos1° x cos2° x cos3° x…………..cos90°) is 1.

Answer: False

Class 10 WBBSE Math Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 Fill In The Blanks

1. The value of (4/sec²θ+ 1/1+ cot²θ +3sin²θ) is————-

Solution: 4/sec² θ + 1/1+ cot²θ +3sin²θ

= 4cos²θ + sin²θ + 3sin²θ

= 4(cos²θ + sin²θ)

= 4 x 1

= 4

2. If sin (θ-30°) = 1/2 then the value of cos e is————

Solution: sin(θ – 30°) = 1/2 = sin30°

θ – 30° = 30°

θ = 30° + 30°              ∴ θ =- 60°

∴ cos θ= cos 60° = 1/2

3. If cos²θ – sin²θ = 1/2 , then the value of Cos⁴θ- sin⁴θ is ———

Solution: Cos⁴θ- sin⁴θ

(cos²θ)² – (sin²θ)²

= (cos²θ + sin²θ)(cos²θ – sin²θ)

= 1 x 1/2

= 1/2

Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 Short Answers

1. If r cosθ = 2√3, r sinθ = 2, and 0º <θ <90º, then let us determine the values of both r and θ

Solution:

If r cosθ = 2√3, r sinθ = 2, and 0º <θ <90º

r cosθ = 2√3, r sinθ = 2

⇒ \(\frac{r \sin \theta}{r \cos \theta}=\frac{2}{2 \sqrt{3}}  or, \tan \theta=\frac{1}{\sqrt{3}}=\tan 30^{\circ}\)

∴ θ = 30°

Again, \(r^2 \cos ^2 \theta+r^2 \sin ^2 \theta=(2 \sqrt{3})^2+2^2\)

Or, \(r^2\left(\cos ^2 \theta+\sin ^2 \theta\right)=12+4=16\)

Or, \(r^2 \times 1=16\)

Or, \(x=\sqrt{16} \pm 4\)

2. If sinA + sinB = 2 where 0° SA≤ 90° and 0° B≤ 90°, then let us find out the value of (cosA+ cosB).

Solution.

If sinA + sinB = 2 where 0° SA≤ 90° and 0° B≤ 90°,

sinA + sinB = 2 

Greatest value of sinA          ∴ sin A = sin90°      ∴ A= 90°

Greatest value of sinB         ∴  sin B = sin90°        ∴ B = 90°

cosA + cosB = cos90° + cos90° = 0 + 0 = 0

3. If 0°<θ< 90°, then let us calculate the least value of (9tan²θ + 4cot2θ).

Solution. 9tan²θ+4cot²θ = (3tanθ)² + (2cot²θ)²

= (3tanθ2-cotθ)²-2. 3tanθ. 2cotθ

= (3tanθ-2cotθ)²-12 tanθ x 1/tanθ

∴ Least value of (9tan²θ+ 4cot²θ) is 12.

4. Let us calculate the value of ( Sin⁶+cos⁶+ 3sin²α cos²α).

Solution:  Sin⁶∝+cos⁶∝+3sin²α cos²α.

= (sin²α)³ + (cos²α)³ + 3. sin²a. cos²α(sin²α + cos²α)

= (sin²α + cos²α)³ = (1)³

= 1.

5. If cosec2θ = 2cote and 0° <0< 90°, then let us determine the value of 0.

Solution.

If cosec2θ = 2cote and 0° <0< 90°

cosec²θ = 2cote

or, 1+ cot²θ – 2cotθ = 0

or, (1 – cote)² = 0

1-cotθ=0               ∴ cotθ1 = cot45°

∴ 0 = 45°