WBCHSE Class 11 Chemistry Notes On Rutherford Atomic Model
Ernest Rutherford, a physicist from New Zealand, decided to test the validity of Thomson’s model by bombarding a thin gold foil with a-particles. The idea was that the incident charged particles would be deflected by the charged particles in the gold atoms and that the amount of deflection would indicate how exactly the charged particles are distributed in the atom.
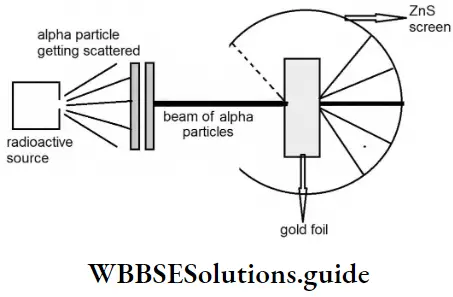
The thickness of the gold foil used by Rutherford was 4 x 10-5 cm. A circular screen coated with ZnS was placed around the foil to detect the deflected a-particles. The tiny flashes made by the a-particles on the screen coated with ZnS would make them detectable.
Rutherford made the following observations.
- Most of the α-particles passed right through the foil without being deflected.
- A small fraction of the a-particles were deflected by small angles.
- Just a few particles (about 1 in 20,000) were deflected by very large angles or reflected right back.
Read and Learn More WBCHSE For Class11 Basic Chemistry Notes
The last observation was something totally unexpected and paved the way for a new picture of the atom. Rutherford came to the following conclusions from his observations.
| Class 11 Biology | Class 11 Chemistry |
| Class 11 Chemistry | Class 11 Physics |
| Class 11 Biology MCQs | Class 11 Physics MCQs |
| Class 11 Biology | Class 11 Physics Notes |
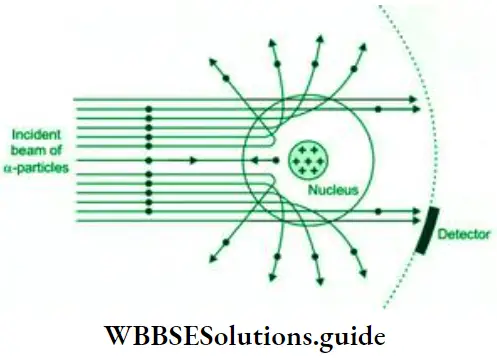
- Since most of the α-particles passed undeflected through the gold foil, the charge inside the gold atoms could not be evenly distributed. There had to be large empty spaces inside the atom. In fact, most of the space inside the atom must be empty.
- Thomson’s model of evenly distributed positive charge could not explain the violent deflection of the α-particles which were reflected right back. It would need a far more concentrated positive charge to produce such an impact. The fact that only 1 in 20,000 α-particles encountered such a repulsive force also pointed in the direction of a concentration of the positive charge in a small portion of the gold atom.

Rutherford’s Model Of The Atom
The conclusions drawn from the scattering experiment prompted Rutherford to put forward a nuclear model of the atom. The salient features of his model are as follows.
- Most of the mass and all the positive charge of an atom is concentrated in a very small region (radius of the order of 10-13cm). Rutherford called this region the nucleus of the atom. You can imagine the difference in size of the nucleus and the atom if the radius of the atom is of the order of 10-8 cm.
- The nucleus is surrounded by electrons with negligible mass which revolve around it at very high speeds, just as the planets revolve around the sun.
- The total negative charge on the electrons of an atom is equal to the total positive charge on the nucleus, making the atom as a whole electrically neutral. The positive charge of the nucleus is due to protons present in it.
- Most of the space inside the atom is empty.
Rutherford received the Nobel prize for his work in Chemistry in 1908.

Discovery Of The Neutron
Rutherford’s experiment provided a method of determining the positive charge on the nucleus of an atom. By counting the number of a-particles scattered in different directions, it was possible to count the positive charge on the nucleus.
“WBCHSE Class 11 Chemistry, Rutherford atomic model, and its limitations”
- It was observed that the charge on the nucleus of an atom is always an integral multiple of the charge on an electron. This integral value was called the atomic number (Z) of an atom and was supposed to be equal to the number of positive particles or protons in the nucleus. Obviously, for the atom to be electrically neutral, there had to be Z electrons revolving around the nucleus.
- The next difficulty was accounting for the mass of the atom. The number of protons and electrons determined by the a-particle-scattering experiment could not account for the mass of the atom. Sir James Chadwick, a British physicist, solved this problem by discovering the neutron in 1932.
- He found that highly penetrating rays consisting of electrically neutral particles were produced when a thin foil of beryllium was bombarded with fast-moving a-particles. These neutral particles turned out to have the same mass (1.675 x 10-24 g) as the proton and were called neutrons.
Atomic Number And Mass Number
Rutherford’s experiment had provided a means of determining the positive charge on the nucleus of an atom. A British physicist called H G J Moseley devised a finer method of determining the positive charge on the nucleus by determining the wavelength of the X-rays emitted by an element.
The number of positive charges on the nucleus of an atom was designated the atomic number, Z, as mentioned earlier.
- Chadwick’s discovery was actually a confirmation of what scientists had been hypothesising when they found that the number of protons and electrons in the atom could not account for its mass. In fact, electrons are so light that they hardly contribute anything to the atomic mass.
- Most of the mass of the atom is due to the protons and neutrons in the nucleus, which are together called nucleons. The total number of nucleons in an atom is called its mass number, A. Hence, the mass number of an element = number of protons + number of neutrons. The mass number and atomic number of an element X is indicated as \({ }_Z^A X\). In the case of carbon, it would be indicated as \({ }_6^12 C\).
Isotopes Atoms of the same element have the same number of protons (atomic number), but may not have the same number of neutrons. Atoms of such elements which have the same number of protons but different numbers of neutrons are called isotopes.
- Hydrogen, for instance, has three isotopes—\({ }_1^1 H\) (protium), \({ }_1^2 H\) (deuterium), and \({ }_1^3 H\) (tritium). In the case of hydrogen, the three isotopes have different names, but this is not the case with other elements. Some of the other examples are \({ }_17^35 Cl\) and \({ }_17^37 Cl\).
- It is important to mention here that the isotopes behave nearly the same chemically. This is because the chemical properties of an atom (or element) depend on the number of electrons that actually participate in bond formation. The number of electrons in an atom are determined by the number of protons and not neutrons.
“Rutherford atomic model, WBCHSE Class 11, chemistry notes, and key concepts”
Isobars Atoms of different elements sometimes have the same mass number. Obviously, they have different atomic numbers and different chemical properties, example, \({ }_{19}^{40} \mathrm{~K} \text { and }{ }_{20}^{40} \mathrm{Ca}\). Isotopes differ in the number of neutrons, whereas isobars differ both in the number of protons and neutrons.
Isotones When atoms of different elements have the same number of neutrons, they are called isolones. For instance, \({ }_7^{15} \mathrm{~N} \text { and }{ }_8^{16} \mathrm{O}\) are isotones. Another example is \({ }_11^{23} \mathrm{~Na} \text { and }{ }_12^{24} \mathrm{Mg}\).
Class 11 WBCHSE Chemistry Notes on Atomic Structure and Rutherford’s Model
Example 1. Calculate the number of electrons which will together weigh 3 g.
Solution:
Given
weigh 3 g
Mass of1 electron = 9.11 x10-31 kg
or, 9.11 x10-31 kg is mass of 1 electron.
∴ 3 g or 3 x10-3 kg is mass of \(\frac{1}{9.11 \times 10^{-31} \mathrm{~kg}} \times 3 \times 10^{-3} \mathrm{~kg}\) = 3.294 x1027electrons.
Example 2. Calculate the mass and charge of 2 moles of electrons.
Solution:
Given
1 mole contains 6.022 x 1023 electrons.
Mass of 1 electron = 9.11 x10-31 kg.
Mass of 2 moles of electrons = (9.11 x 1031) kg x 2 x 6.022 x1023 = 10.972 x10-7=1.0972 x10-6 kg.
Charge on one electron =1602 x10-19 coulombs.
∴ charge on 2 moles of electrons =1602 x10-19 coulomb x 2 x 6.022 x 1023 =1930 x 105 coulombs.
“WBCHSE Class 11, chemistry notes, on Rutherford’s model, structure, and limitations”
Example 3. Find the number and mass of neutrons in 32 mg of O2 at stp (mass of a neutron =1675 x 10-27 kg).
Solution:
Given
32 mg of O2 at stp (mass of a neutron =1675 x 10-27 kg)
1 mole of O2 =16 g = (6.022 x1023) x (8 + 8) neutrons = 9.6352 x1024 neutrons.
Now, 16 g of O2 =1 mole.
∴ 32 g of O2 = 2 moles
or, 32 mg of O2 = 0.002 moles
Number of neutrons in 32 mg of O2 = 9.6352 x 1024 x 2 x10-3 =19270 x 1022.
Mass of 1 neutron =1675 x 10-27 kg.
∴ mass of 19270 x 1022 neutrons =19270 x 1022 x1675 x 10-27 = 3.228 x 10-5 kg.
Electromagnetic Waves
The Rutherford model of the atom explained the results of the a-partide-scattering experiment very successfully, so it was accepted for a while. But when sdentists tried to find explanations for the arrangement of electrons in the atom, the stability of the atom, and in particular, atomic spectra (characteristic light emitted by an atom) in terms of the Rutherford model, they failed completely. The theory did not match experimental observations.
To understand how the Rutherford model failed, we must first know something about atomic spectra, or rather about the nature of electromagnetic waves. Light is just a kind of electromagnetic radiation, as you may already know.
Electromagnetic Wave theory: Newton and his contemporaries thought of light as a stream of particles/ called corpuscles of light. Newton’s corpuscular theory of light could explain certain phenomena, like reflection and refraction but not others, like interference and diffraction.
It was, therefore, discarded and the wave theory of light replaced it. According to the wave theory, light, or rather electromagnetic radiation, is propagated in the form of waves, and waves are characterized by wavelength (λ—Greek letter lambda) and frequency (ν—Greek letter nu). The speed of propagation is given by
∴ c = vX.
This speed is constant for all electromagnetic radiation (in vacuum) and is equal to 3.00 x 108 ms-1. You will learn more about the wave theory later. For the moment it will suffice to remember the following points.
- In 1856, James Clark Maxwell, a British physicist, first showed that light is a form of electromagnetic radiation. And, in addition to light (visible form of radiation), there are other forms of electromagnetic radiation like heat and ultraviolet radiation.
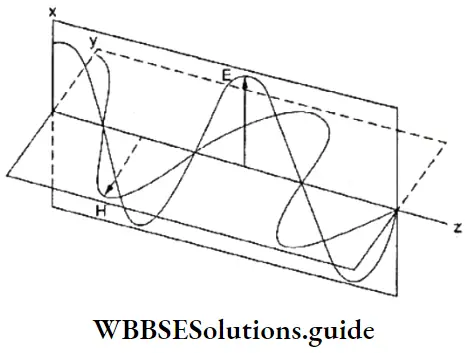
- Electromagnetic radiation comprises electric and magnetic fields oscillating at right angles to each other.
- In any electromagnetic radiation, the direction of propagation, direction of the electric field, and the direction of the magnetic field are at right angles to each other.
- Electromagnetic radiation does not need a material medium for propagation. The speed of propagation of electromagnetic radiation through vacuum is constant (c). Different forms of radiation differ only in their frequency and wavelength, since the speed of propagation (c), which is the product of the frequency and wavelength, is constant. wave are mutually perpendicular.
Electromagnetic Characteristics of a Wave: You have just read that any electromagnetic radiation travels with a particular speed in vacuum, and that what distinguishes one form of radiation from another is its characteristic wavelength and frequency. What exactly are the wavelength and frequency of a wave?
1. Wavelength Is the distance travelled by the wave in one cycle, or the distance between neighboring crests or troughs of the wave. It is generally measured in Angstrom units (A) or nanometres (nm). 1 A = 10-10 m; 1 nm = 10-9 m.
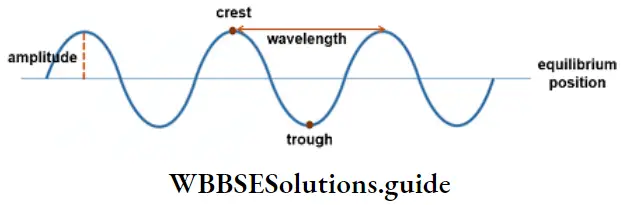
2. Frequency The frequency of n radiation can be defined as the number of waves which pass through a particular point In one second, It is measured in hertz (Hz) or cycles per second (cps).
∴ 1cps = 1 Hz
One cycle is said to be completed when a wave consisting of a crest and a trough passes through a point.
3. Wave number The wave number may be defined as the number of wavelengths per centimeter and is equal to the inverse of the wavelength expressed in centimetres. It is denoted by \(\bar{v}\)(nu bar) and its unit is cm-1 (centimeter inverse).
∴ \(\bar{v}=\frac{1}{\lambda} \mathrm{cm}^{-1}\)
4. Amplitude It is the height of the crest or the depth of the trough of a wave. It is generally denoted by a. The amplitude of the wave determines the intensity of radiation, which is the energy per unit volume of the wave.
“Rutherford atomic model, discovery, gold foil experiment, and drawbacks, WBCHSE syllabus”
Example 1. A radio station broadcasts on a frequency of 1.360 kHz. Calculate the wavelength of the radiation emitted by the transmitter of the station.
Solution:
Given
A radio station broadcasts on a frequency of 1.360 kHz.
Frequency (v) = 1360 kHz = 1.360 x 103 Hz.
Velocity (c) = 3 x 108 m s-1
∴ wavelength (λ) = \(\frac{c}{v}=\frac{3 \times 10^8}{1360 \times 10^3}=219.3 \mathrm{~m}\)= 219.3 m.
Example 2. The wavelength of the light emitted by a source in a laboratory is 700 nm. Calculate its frequency.
Solution:
Given
The wavelength of the light emitted by a source in a laboratory is 700 nm.
Wavelength (λ) = 700 nm = 7 x 10-7 m.
Velocity (c) = 3 x 108 m s-1
∴ frequency (v) = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{7 \times 10^{-7}}=4.28 \times 10^{14} \mathrm{~s}^{-1}\).
Electromagnetic Failure of Wave Theory: The wave theory of light could not provide the complete picture of the nature of light. Two major phenomena that the wave theory could not explain are photoelectric emission and black-body radiation.
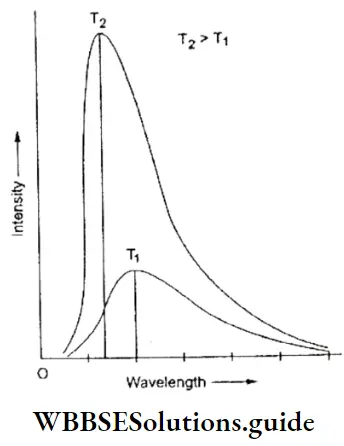
Electromagnetic Black-body radiation You may have noticed that objects change colour when they are heated. The element of a heater, for example, is red first, then orange, and then yellowish, which means that the kind of light (frequency of radiation) an object emits depends on its temperature.
Actually, a hot body emits a whole range of radiations, and what varies with its temperature is the intensity of these radiations. A particular radiation (say red) is most intense at a particular temperature.
- The intensities of the various radiations emitted by a hot body depend on its temperature. A body which emits and absorbs all radiations is called a black body. The intensities of radiations of different wavelengths emitted by a black body at different temperatures were obtained experimentally. These observations could not be explained by the wave theory of light.
- Photoelectric effect Another phenomenon which the wave theory could not explain is the photoelectric effect. When a beam of monochromatic light (light of a single wavelength) falls on a clear metallic surface in vacuum, the metal emits electrons.
- This is called the photoelectric effect and the electrons emitted by the metal are called photoelectrons. It was observed that the energy of the photoelectrons increases with the frequency of the light falling on the metal. Also if the frequency of the incident light falls below a certain critical value or threshold frequency, the emission of electrons stops.
- This threshold frequency is different for different metals. Light of frequency less than the threshold frequency cannot eject electrons no matter how long it falls on the surface or how high is its intensity.
- Also, the intensity of the incident radiation has no impact on the energy of the photoelectrons emitted although the number of electrons ejected does depend on the intensity of incident light.
- The wave theory of light could not explain why the energy of the photoelectrons should remain unaffected when the intensity of the incident radiation increases, nor why it should increase when the frequency of the radiation increases. According to the wave theory the energy carried by a radiation depends on its intensity (amplitude) and not on its frequency.
Electromagnetic Planck’s theory: Max Planck, a German physicist, proposed a theory that could explain black-body radiation. He showed that the radiation emitted by such a body and the way it changed with temperature (energy distribution as a function of temperature) could be explained if one assumed that radiant energy (energy of radiation) is emitted and absorbed in the form of packets. You will read about Planck’s theory in detail later. Just the salient features of this theory will suffice for the present discussion.
1. Radiant energy is not emitted or absorbed continuously but discontinuously, in the form of small packets called quanta. Each wave packet or quantum is associated with a definite amount of energy. The term photon is often used while referring to a packet of energy in the case of light.
2. The amount of energy associated with a quantum of radiation is proportional to the frequency of the radiation.
∴ E ∝ v
or E = hv or E = \(h \frac{c}{\lambda},\)
where h is the Planck constant and is equal to 6.626 x 10-34 J s.
3. A body can emit or absorb energy only in integral multiples of hv, i.e., hv, 2hv,3hv, etc. It cannot emit or absorb fractional values of hv.
Planck’s theory explained the distribution of intensity of radiation from a black body as a function of frequency at different temperatures. However, the theory could not explain why energies should be quantised in this manner.
Example 1. Calculate the energy of one photon of ultraviolet light of wavelength 100 nm.
Solution:
Wavelength, λ = 100 nm.
∴ frequency \(\mathrm{v}=\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{100 \times 10^{-9} \mathrm{~m}}=3 \times 10^{15} \mathrm{~s}^{-1}\)
Energy of photon, E = hv = 6.626×10-34 x 3 x 1015 = 1.987 x 10-18 J
“WBCHSE Class 11 Chemistry, Rutherford’s experiment, postulates, and limitations”
Example 2. How many photons of light of wavelength 4000 pm would provide 1 J of energy?
Solution:
Energy of photon (E) = hv = h c/λ
∴ E =\(\frac{6.626 \times 10^{-4} \mathrm{~J} \mathrm{~s} \times 3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{4000 \times 10^{-12} \mathrm{~m}}=4.9695 \times 10^{-17} \mathrm{~J}\)
∴ 4.9695 x 10-17 J is provided by 1 photon.
∴ 1 J will be provided by \(\frac{1 \mathrm{~J}}{4.9695 \times 10^{-17} \mathrm{~J}}=2.012 \times 10^{16}\) photons.
Einstein’s explanation for the photoelectric effect: In 1905, Albert Einstein showed that if one extended Planck’s theory (which talked only about absorption and emission) to the propagation of radiation, one could explain the phenomenon of photoelectricity quite easily.
According to the quantum theory (Planck’s theory) of radiation, the energy of a photon is proportional to its frequency. Obviously, then the energy of photoelectrons emitted by a metal surface increases with the frequency of the light falling upon it. How?
- To understand this clearly, let us take into account the threshold frequency once again. As stated earlier, each metal has its characteristic minimum frequency below which it does not show photoelectric effect.
- This minimum frequency or threshold frequency is represented as v0. If we take the example of potassium, the photoelectric effect is observed in the case of yellow light and not red light. This means that when yellow light falls on the surface of potassium, electrons are emitted. The threshold frequency (v0) for potassium is 5 x 1014 Hz. The frequencies of red light and yellow light are 4.4-4.6 x 1014 Hz and 5.1-5.2 x 1014 Hz respectively. If the striking photon has a frequency greater than the threshold frequency, photoelectric effect occurs.
- When a photon strikes a metal with frequency v and energy hv, some of its energy is used up to eject the electron from the metal atom. This energy is equal to the minimum energy required to eject the electron i.e., hv0 (also called work function W). The remaining energy of the striking photon is transformed into the kinetic energy of the photoelectron. The kinetic energy is equal to \(\frac{1}{2} m_{\mathrm{e}} v^2\) where me is the mass of the photoelectron and v is its velocity. Since the total energy is conserved, we can state that
hv – hv0 = kinetic energy of the electron = \(\frac{1}{2} m_{\mathrm{e}} v^2\)
or, \(h v=\frac{1}{2} m_{\mathrm{e}} v^2+W_0\)

If hv increases (frequency increases), so will \(m_{\mathrm{e}} v^2 / 2\), which is the energy of the photoelectron. Also, an increase in the intensity of the incident radiation means an increase in the number of photons striking the metallic surface. An increase in the number of photons would naturally lead to an increase in the number of photoelectrons produced.
- Planck and Einstein showed that light has a particle or corpuscular nature which explains the photoelectric effect satisfactorily. On the other hand, the phenomena of diffraction and interference definitely show that it has a wave nature.
- The complete picture of the nature of light, thus, includes both its wave and particle nature and it is said that light exhibits a dual character.
“Rutherford atomic model, WBCHSE Class 11, solved examples, and real-world applications”
Example 1. The threshold frequency v0 for a metal is 8.0 x 10-15 s-1. Calculate the kinetic energy of the electron which is ejected when radiation of frequency v = 2.0 x 1016 s-1 hits the metal.
Solution:
Given
The threshold frequency v0 for a metal is 8.0 x 10-15 s-1.
KE of an electron = \(\frac{1}{2}\)mv2 = hv – hv0 where hv0 = work function of the metal.
Now, KE = h(v – v0)
= \(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}\left(2.0 \times 10^{16} \mathrm{~s}^{-1}-8.0 \times 10^{15} \mathrm{~s}^{-1}\right)\)
= \(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times(20-8) 10^{15} \mathrm{~s}^{-1}\)
= \(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 12 \times 10^{15} \mathrm{~s}^{-1}\)
= \(79.512 \times 10^{-19} \mathrm{~J}=7.9 \times 10^{-18} \mathrm{~J}\).
Class 11 Chemistry Rutherford Model vs Bohr Model for WBCHSE Board
Example 2. A photon of wavelength 4x 107 m strikes a metal whose work function is 4.0 x 10-19 J. Calculate the velocity of the ejected electron (mass of electron =9 x 10-31 kg).
Solution:
Given
A photon of wavelength 4x 107 m strikes a metal whose work function is 4.0 x 10-19 J.
KE = hv – hv0
hv = energy of the photon and hv0 = work function.
Now v = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{4 \times 10^{-7}}=7.5 \times 10^{14} \mathrm{~s}^{-1}\).
∴ hv = 6.626 x 10-34 J s x 7.5 x 1014 s-1 = 494 x 10-19 J.
KE = (4.9 x 10-19 – 4.0 x 10-19 J)
= 0.9 x 10-19 or 9 x 10-20 J.
⇒ \(/frca{1}{2}\)mv2 =9 x 10-20 J.
∴ \(v^2=\frac{2 \times 9 \times 10^{-20}}{9 \times 10^{-31}}=2 \times 10^{11}=20 \times 10^{10}\)
∴ \(v=\sqrt{20 \times 10^{10}}=4.5 \times 10^5 \mathrm{~m} \mathrm{~s}^{-1}\)
“Rutherford atomic model, structure of atom, and failure to explain stability, WBCHSE notes”
Atomic Spectra
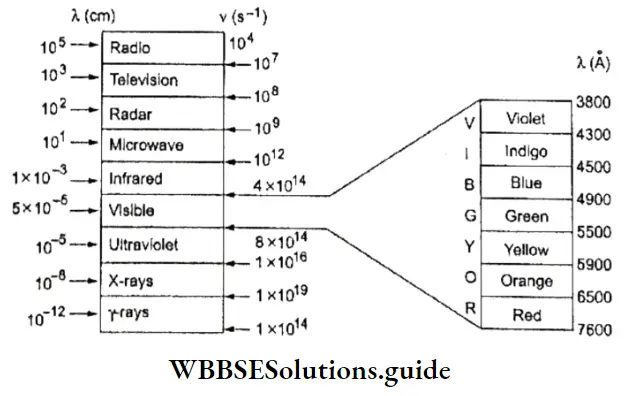
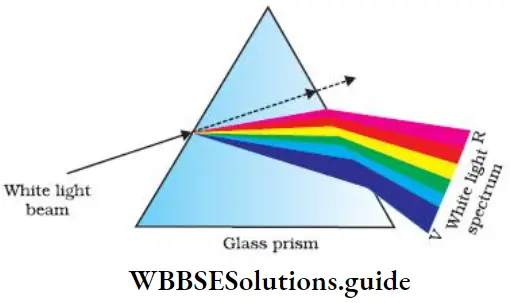
You have already studied that when a beam of ordinary white light is passed through a prism, it gets refracted and splits into a series of colored bands called spectrum (VIBGYOR), the seven constituent colours.
This kind of spectrum is called a continuous spectrum. In a continuous spectrum the different bands of colours merge into each other.
- The spectrum ranges from violet at 750 x 1014 Hz to red at 4 x 1014 Hz. What actually happens is that when the beam of light passes through the prism, it gets deviated and the angle of deviation is directly proportional to the frequency of radiation. Remember that visible light is just a small portion of the electomagnetic radiation.
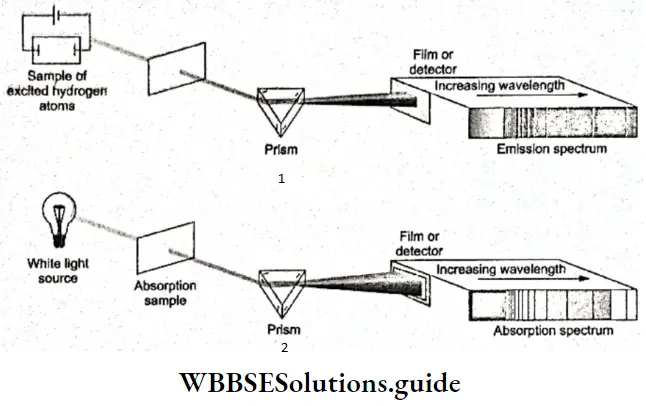
- When electromagnetic radiation interacts with matter, i.e., when energy is supplied to an element either by heating or by some other method like passing an electric discharge, its atoms get excited and emit electromagnetic radiations of definite frequencies on returning to their lower stable energy states.
- This set of radiations of particular frequencies is called the emission spectrum of the element. It is also called the atomic spectrum because the radiations are emitted as a result of energy changes in the atom. The characteristic radiations (of particular frequencies) absorbed by the excited atoms of an element constitute its absorption spectrum.
- Two German physicists, Gustav Robert Kirchhoff and Robert Wilhelm Bunsen, started studying the emission spectra of elements around 1860. Spectra are analyzed with the help of an instrument called a spectroscope. In its simplest form, a spectroscope is a hollow tube with a lens to produce a parallel beam of light that passes through a prism.
- The spectra produced by the excited atoms of elements, unlike the ones produced by white light when passed through a prism, are discontinuous. They generally consist of a few bright lines separated by dark bands. That is why atomic spectra are also called line specif a livery element has its characteristic line spectrum. Thus, atomic spectra are called fingerprints of atoms and are used to identify elements. The study of atomic spectra stalked in the context of chemical analysis, and elements like rubidium, cesium, thallium, indium, gallium, and scandium were discovered this way.
Spectrum of hydrogen: To study the emission spectrum of hydrogen, the gas is taken in a gas-discharge tube at low pressure, and an electric discharge is passed through it. The H2 molecules dissociate into energetically excited hydrogen atoms.
- The radiations emitted by the excited atoms of the gas are passed through a prism and the radiation coming out of the prism is brought to a focus on n photographic film, This is known as spectroscopy. The spectrum obtained this way consists of n large number of sharp lines separated by dark bands. Only the lines in the visible and ultraviolet regions can be obtained this way. The lines in the infrared region require other methods of detection.
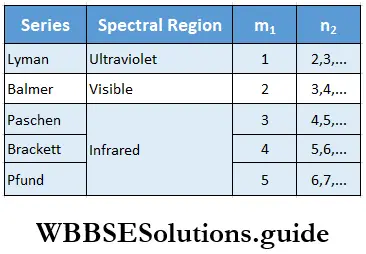
- The emission spectrum of hydrogen has several groups of lines which are divided into different series, named after their discoverers.
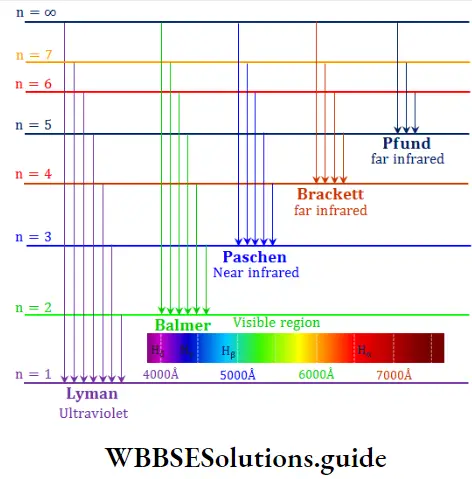
J J Balmer, a Swiss mathematician, studied the spectrum of hydrogen in the visible region and showed that the wave numbers of the spectral lines obey the following formula, known as the Balmer formula.
⇒ \(\bar{v}=\frac{1}{\lambda}=109,677\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \mathrm{cm}^{-1}\)
where n is an integer greater than 2.
Later, J R Rydberg, a Swedish physicist, came up with a more general formula that can be applied to all the series in the hydrogen spectrum.
⇒ \(\overline{\mathrm{v}}=109,677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\)
where n1 and n2 are integers, such that n2>n1
The value 109,677 cm-1 is called the Rydberg constant (R) for hydrogen.
“WBCHSE Class 11 Chemistry, limitations of Rutherford’s model, and need for Bohr’s theory”
Example 1. Calculate the wavelength of the light emitted by a hydrogen atom, given that n1 = 1 and n2 = 4.
Solution:
According to the Rydberg formula,
⇒ \(\frac{1}{\lambda}=\bar{v}\left(\mathrm{~cm}^{-1}\right)=109,677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\)
Given n1 = 1, n2 =4.
∴ \(\quad \bar{v}=109,677\left(\frac{1}{1^2}-\frac{1}{4^2}\right)\)
= \(109,677 \times \frac{15}{16}=102,822 \mathrm{~cm}^{-1}\)
∴ \(\quad \lambda=\frac{1}{\bar{v}}=\frac{1}{102,822}=9.7 \times 10^{-6} \mathrm{~cm}\).
Example 2. Calculate the frequency and the wavelength of the radiation emitted when an electron in the hydrogen atom jumps from the second to the first orbital.
Solution:
According to the Rydberg formula
⇒ \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)
But R = 109,677cm-1,n2 =2 and n1 =1
⇒ \(\bar{v}=109,677\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \mathrm{cm}^{-1}\)
= \(109,677 \times \frac{3}{4} \mathrm{~cm}^{-1}=82257.75 \mathrm{~cm}^{-1}\)
⇒ \(\lambda=\frac{1}{\bar{v}}=\frac{1}{82257.75} \mathrm{~cm}=121.56 \times 10^{-7} \mathrm{~cm}\) = 121 x 10-9 cm
“WBCHSE Class 11, chemistry notes, on Rutherford’s model, and comparison with Bohr’s model”
WBCHSE Chemistry Notes on Atomic Models: Rutherford’s Contributions
Rutherford’s nuclear model of the atom resembled the solar system, with a heavy, positively charged nucleus around which the much lighter electrons were supposed to revolve. Also, the coulomb force (F =q1q2/r2 )which is proportional to the product of the charges and inversely proportional to the square of the distance between them, is mathematically similar to the gravitational force (Gm1m2/r2) between a planet and the sun.
It was natural, therefore, for scientists to think that the motion of electrons around the nucleus should be similar to the motion of planets around the sun. Applying the Newtonian theory to the solar system, it had been shown earlier that planets move in definite orbits around the sun.
“Rutherford atomic model, nucleus discovery, electron orbit issues, and WBCHSE syllabus”
- However, a problem arose when this concept was applied to the atom. If electrons were to move around the nucleus in well-defined orbits, they would have to be in a constant state of acceleration (even a body moving with constant speed in an orbit is accelerating because it is changing direction continuously).
- This would lead to an impossible situation according to Maxwell’s electromagnetic theory, which says that when charged particles are accelerated they emit electromagnetic radiation.
- If an electron moving around the nucleus were to emit radiation constantly, it would slow down because the energy of the radiation emitted by the electron would come from the motion of the electron. Thus, the orbit of the electron would keep shrinking and the electron would follow a path resembling a spiral and ultimately fall into the nucleus.
This would lead to the collapse of the atom (such a thing does not happen in the case of planets because they are uncharged bodies). Rutherford’s model of the atom could not explain its stability in terms of Newtonian mechanics and Maxwell’s electromagnetic theory.
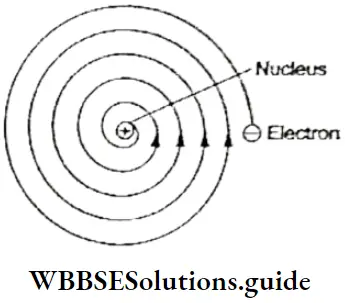
- Nor could it explain the line spectra associated with atoms. According to Maxwell’s theory, the frequency of radiation emitted by a charged body is equal to its frequency of revolution.
- So, the frequency of the radiation emitted by Rutherford’s electron, following Newtonian mechanics and Maxwell’s theory, would change continuously as its orbit and, consequently, its frequency of revolution would change. This would lead to atomic spectra being continuous, rather than discrete (line spectra), as observed experimentally.
- Thus, Rutherford’s model, with its concentration of positive charge in the nucleus, could explain the scattering experiment, but its planetary electrons could neither account for the stability of the atom nor the line spectra exhibited by excited atoms. It says nothing about how the electrons are distributed around the nucleus and what are the energies of these electrons.
