WBBSE Class 10 Model Question Paper 2023 Mathematics set 1

Model Question Paper 2023 Mathematics set 1

 

Model Question Paper 2023 Mathematics set 1 MCQs

 

Question 1. Compound interest and simple interest are equal at the same rate of interest per annum in

1. 1 year
2. 2 years
3. 3 years
4. 4 years

Answer. 1. 1 year

Question 2. If the ratio of principal and simple interest is 10: 3, for 5 years, the rate of interest per annum will be 

1. 3
2. 30
3. 6
4. 12

Answer. 3. 6

Question 3. Which one is not a quadratic equation given below?

1. 2x-3×2 = 3×2 + 5
2. (2x+3)2=2(x2 – 5)
3. (√3 + 2)2 = 3×2-7
4. (x-2)2=5×2 + 2x – 3

Answer. 3. (√3 + 2)2= 3×2-7

Question 4. If the roots are equal to the quadratic equation 4×2 + 6kx+9= 0, the value of k

1. 2 or 0
2. -2 or 0
3. 2 or -2
4. only 0

Answer. 3. 2 or -2

Question 5. In the adjoining figure, ZOAB = 50° of a circle with center O and if C is any point on the circle, the value of ZACB is

1. 50°
2. 40°
3. 80°
4. 100°

Answer. 2. 40°

 

 

Question 6. AB and CD are two equal chords of a circle with center O. If ZAOB = 70°, the value of COD is

1. 110°
2. 70°
3. 35°
4. 80°

Answer. 2. 70°

Question 2. Answer the following questions:

1. In how many years the interest will be 3/4th of the principal at the rate of interest 10° simple interest per annum?

Solution : I = prh/100

3x/5 = x x 10 x h / 100

∴ t=6.

2. If p: q=5:7 and p-q=-4, what is the value of (3p – 2q)?

Solution: Let p = 5k, q = 7k

∴ 5k – 7k = -4

∴ k = 2

∴3p – 2q 

= 3 x 10-2 x 14

= 30-28 

= 2.

The value of (3p – 2q) = 2.

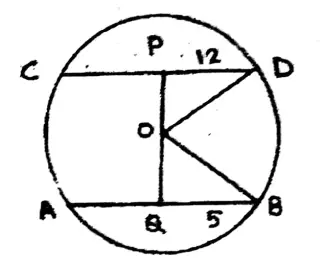
3. Two parallel chords of a circle with center O lie opposite to the center. If AB = 10 cm, CD = 24 cm, and if the distance between the two chords AB and CD is 17 cm, find the radius of that circle.

Solution:

Given

Two parallel chords of a circle with center O lie opposite to the center. If AB = 10 cm, CD = 24 cm, and if the distance between the two chords AB and CD is 17 cm

OD² = OP² + PD²

OB = OQ² + QB²

OD = OB      ∴ OP²+ PD² = OQ² + QB²

Let OP = x, OQ = 17 – x

x² + 12² = (17-x)² + x²

x² – 34x + 289 + x² = x² + 144

x²-34x+145 = 0

(x+29) (x-5)= 0

∴ x = 5

∴The radius of that circle = 5

 

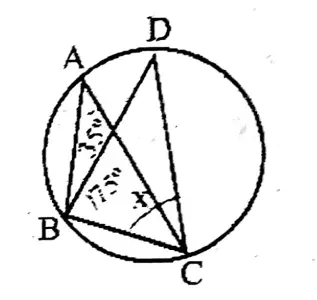
4. In the adjoining figure find the value of x.

Solution: BDC = BAC = 35

In ∠BCD, ∠BDC + 75° + x = 180°

or, 35° + 75 + x = 180°

∴ x = 180-110 = 70.

5. If the volume of a cube is 512 cubic cm, find the total surface area of that cube. 

Solution: a³ = 512    Where a = one side

a = √5128 cm.

Total Surface area = 6a² = 6 (8)² = 384 square.

 

Question 3. In how many years will Rs. 1,00,000 amounts to Rs. 1,33,100 at 10% compound interest per annum.

Solution:

Or, The length of a tree increases by 20% every year; if the present length of the tree is 28.8 meters, let us find what was the length three years before.

Solution:

 

Question 4.

1. (2x+1) + 3/2x+1 = 4, (x ≠ – 1/2)

Solution:

 

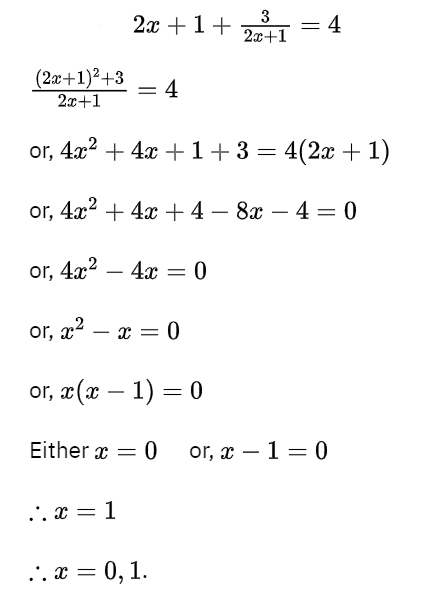
2. 1/(x-2)(x-4) + 1/(x-4)(x-6) + 1/(x-6)(x-8) + 1/3 = 0, (x≠2,4,6,8)

Solution:

Given

 

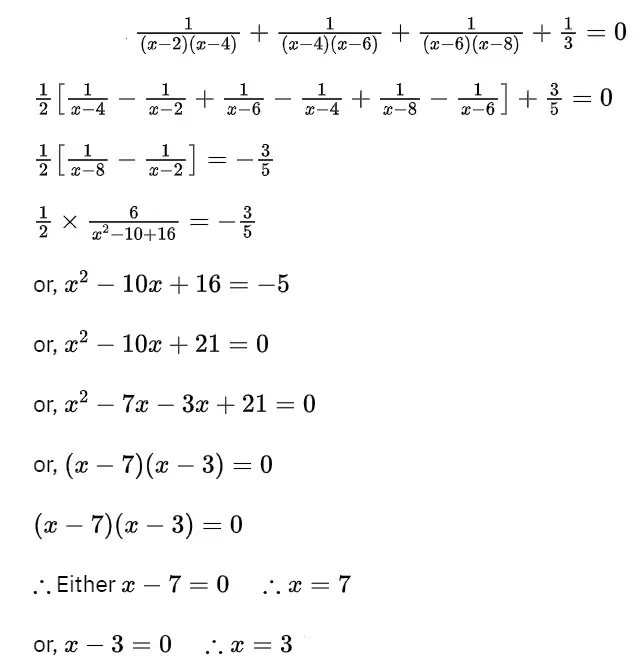
Question 5. Sujata drew a right-angled triangle having a hypotenuse of 13 cm in length, and the difference between the other two sides is 7 cm. Find the length of the other two sides of a right-angled triangle drawn by Sujata.

Solution:

Given

Sujata drew a right-angled triangle having a hypotenuse of 13 cm in length, and the difference between the other two sides is 7 cm.

Let AB = x cm & BC = x – 7

∴ AB2+ BC2 = AC2

x2+(7-x)2 = 132

or, x2 +49 + x2 – 14x = 169

or, 2×2- 14x-120 = 0 or, x2-7x-60 = 0

(x-12) (x+5)=0

∴ x-12=0

x = 12

One side = 12 cm another side = 12-75 cm.

Or, If a two-digit positive number is multiplied by its unit digit, the value of the product is 189 and the tens digit is twice its unit digit, find the unit digit of the number. Solution: Let two-digit number = 10y + x

Given

If a two-digit positive number is multiplied by its unit digit, the value of the product is 189 and the tens digit is twice its unit digit

∴ According to the given conditions,

(10y+x) x = 189

x²+10xy = 189         & y = 2x

10x. 2x + x² = 189

20x²+ x² = 189

21x² = 189

189/21 = 9

∴ x = √9

= 3

y = 6

Required number = 10y+ x = 63.

Question 6. If a, b, c, d are in continued proportion, prove that (a² + b² + c²) (b² + c² + d²) = (ab + bc + cd)²

Solution: Let = a/b = b/c = c/d = k

∴  a = bk, b = ck, c = dk

 L.H.S. = (b²k²+ c²k² + d²k²) (c²k² + d²k² + d²)

= (c²K⁴+ c²k² + d²k²) (d²K⁴+ d²k² + d²k² + d²)

= (d²k + d²K⁴+ d²k²) (d²K⁴+ d²K⁴+ d²k² + d²k² + d²) d²k²(K⁴+k² + 1) d²(k + k² + 1)

= d⁴k²(k + k² + 1)²

R.H.S. = (ab + bc + cd)²

= (bkb + ck.c + dk.d)²

= (b²k + c²k + d²k)²

= (d²k⁶+ d²k³ + d²k)²

= {d²k(K⁴+ k²+ 1)}²

=d⁴k²(K⁴+k² + 1)2 

∴ L.H.S. = R.H.S.

 

Or, if a = √5+1/√5-1 and ab= 1, find the value of(a/b +b/a)

Solution: a = √5+1/√5-1

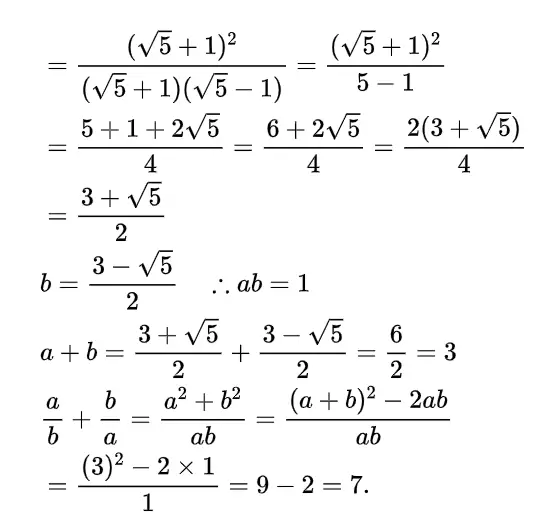
Question 7. Prove that the angle at which an arc of a circle subtends at the center is double any angle subtended by it on the circle.

Solution:

Given: ∠AOB is the angle at the center of the circle with center O and ∠ACB is the angle at any point on the circle formed by circular arc ZAPB.

To Prove: ∠AOB = 2∠ACB

According to the length of the circular arc APB, these may be of three types. In 1 and APB are minor arcs. In 2 APB is a semi-circular arc, and in 3 APB is a major arc.

Construction: C and O are joined and CO is extended up to point D.

Proof: In ΔAOC, OA = OC in each case [radii of the same circle]

∴ ∠OCA = ∠OAC

Again, in each case, the side CO of ΔAOC is extended up to point D. Exterior ∠AOD = ∠OAC + ∠OCA

=2∠OCA——(1)                [ ∠OAC = ∠OCA]

In ΔBOC, OB OC in each case [radii of the same circle] Again, since side CO of ABOC is extended up to point D.

∴ Exterior BOD = ∠OCB +∠OBC

= 2∠OCB——-(2)              [ ∠OBC = ∠OCB]

In 1 and 2 ∠AOD + ∠BOD = 2∠OCA + 2∠OCB [we get from 1 & 2]

∴ ∠AOB = 2(∠OCA + ∠OCB) = 2∠ACB (3)

∴ ∠AOB = 2∠ACB

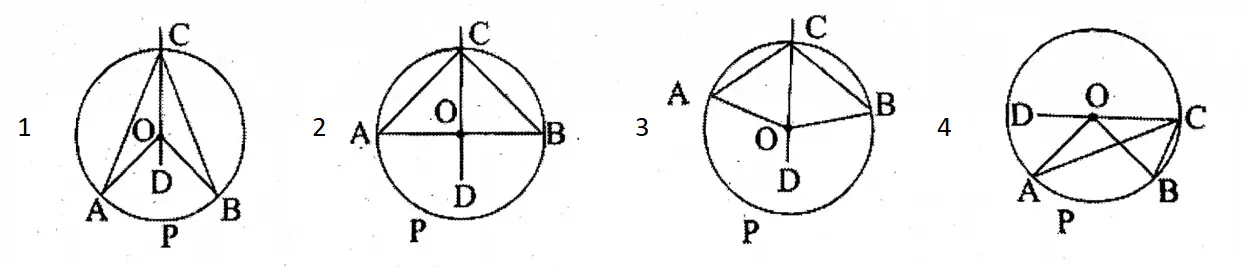
In 4 BOD ∠AOD = 2∠OCB-2∠OCA

Or, ∠AOB = 2∠OCB-2∠OCA

Or, ∠AOB = 2(∠OCB – ∠OCA)

∴ ∠AOB = 2∠ACB. Proved.

 

Or, Prove that the line drawn through the center of a circle bisects a chord, which is not a diameter, is perpendicular to the chord.

Solution :

Given AB is a chord of the circle with its center at O, which is

not a diameter, and OD, is perpendicular to the chord AB.

To prove: CD, bisects the chord AB, i.e., AD = DB. Construction: O, A, and O, B are joined.

Proof: OD is perpendicular to the chord AB.

∴ ΔODA and ΔODB are right-angled triangles.

∴ In right-angled ΔODA and ΔODB, ΔODA =ΔODB (Each is a right angle)

Hypotenuse OA = Hypotenuse OB [radii of the same circle] and OD is a common side.

∴ ΔODA

ΔODB [By R.H.S. axiom of congruency]

∴ AD = DB [Corresponding sides of the congruent triangles] Proved.

Question 8. A reservoir of 21 dcm in length, 11 dcm in breadth, and 6 dcm in depth are filled half with water. How much dem will the water level be raised if 100 iron balls each of which has a 21 cm diameter be completely immersed in it?

Solution:

Given

A reservoir of 21 dcm in length, 11 dcm in breadth, and 6 dcm in depth are filled half with water.

Radius of cylinder (r) = 21/2 cm. 

The volume of one cylinder π(21/2)² x 20 cu cm.

The volume of 100 cylinders = 100 x π x (21/2)² x 20 cu cm.

Let the level of water increase by x dcm. 

The volume of 100 cylinder = Volume of increased water

or, 100 x л x (21/2)² x 20

= 210 x 110 x 10x

x = 100 x 22/7 x 21/2 x 21/2 x 20  /  210 x 110 x 10

= 30 cm 

= 3 dcm.

 

Or, The ratio of the height of a right circular solid cylinder and the length of the radius of the base is 3:1. If the volume of the cylinder is 1029 π cubic cm, what will be the total surface area of the cylinder?

Solution:

Given

The ratio of the height of a right circular solid cylinder and the length of the radius of the base is 3:1. If the volume of the cylinder is 1029 π cubic cm,

Let height = 3x, and radius = x

∴ Volume = x². 3x = 1029

∴ 3x² = 1029

x³= 343 

∴ x = 7

∴ radius = 7 cm, height = 3 x 7 = 21 cm.

Total surface area

= 2 Area of base + Surface area

= 2 πг² + 2πгh

= 2лr(г + h)

= 2 x 22/7 x 7(7+21)

= 44 x 28 sq cm. 

= 1232 sq cm.

Total surface area of the cylinder = 1232 sq cm.