WBBSE Solutions For Class 10 Maths Chapter 10 Theorems Related To Cyclic Quadrilateral Exercise 10.1
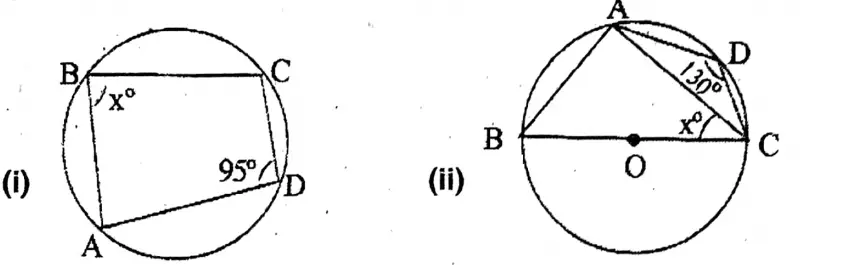
Question 1. Look at the picture of two circles with centre O given below and let us write by calculating the value of x° in each case.
Solution:
Read and Learn More WBBSE Solutions For Class 10 Maths
1. ABCD is a cyclic quadrilateral.
∴ ∠ABC + ∠ADC
180° – 130° = 50°
∴ x = 50.
2. ABCD is a cyclic quadrilateral.
∴ ∠ABC + ∠ADC = 180°
∴ ∠ABC = 50°
Again, ∠BAC = one right angle
∴ ∠BAC = 90°
∴ x° + ∠ABC + ∠BAC = 180°
∴ x° + 50° + 90° = 180°;
∴ x = 40°
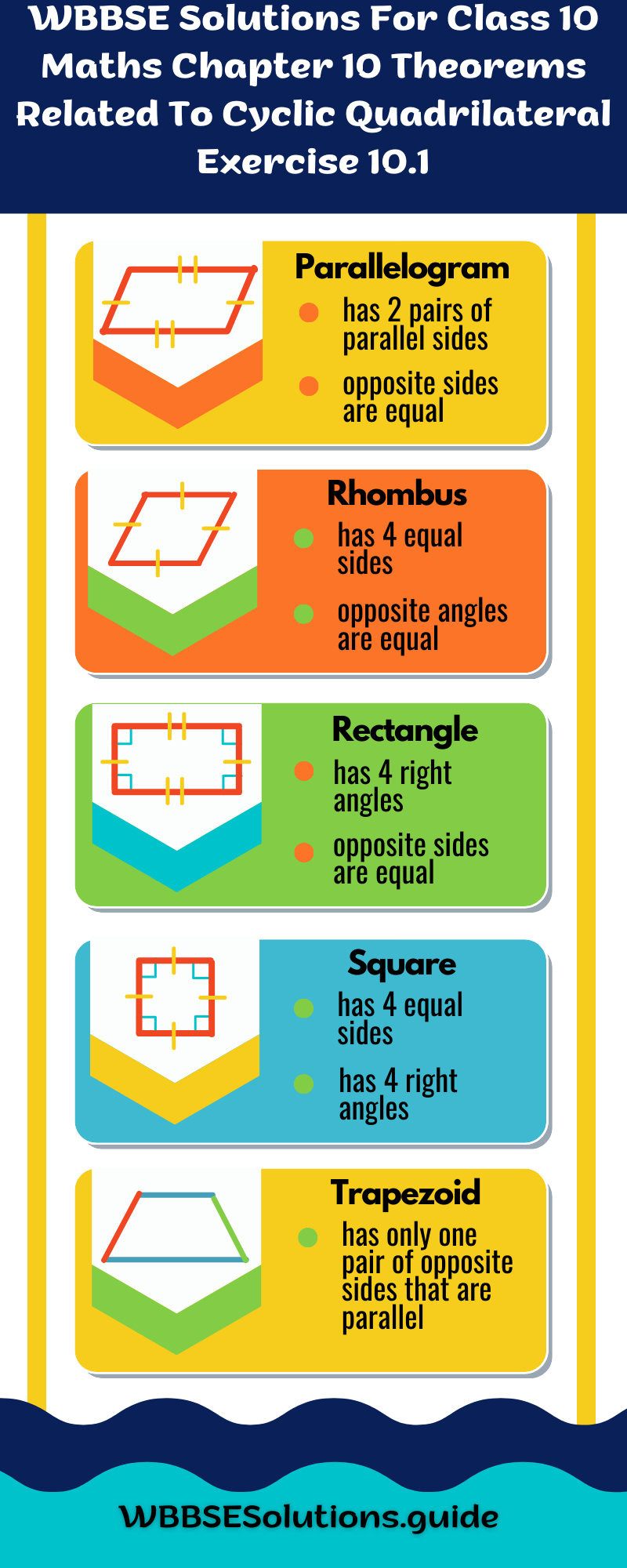
Question 2. ABCD is a cyclic quadrilateral and O is the centre of that circle. If <COD 120° and <BAC 30°, let us write by calculating the value of <BOC and <BCD.
Solution: ∠BOC is angle at the centre and ∠BAC is angle at the circle standing on the Same minor arcBC.
∴ ∠BOC = 2∠BAC = 60°
∠COD is the angle at the centre and ∠CAD is the angle at the circle standing on the same minor arcCD.
∴ \(\angle \mathrm{CAD}=\frac{1}{2} \angle \mathrm{COD}=\frac{1}{2} \times 120^{\circ}=60^{\circ}\)
∴ ∠BAC = 30° + 60° = 90°
∴ In concyclic quadrilateral ABCD, ∠BCD + ∠BAD = 1
∴ ∠BCD = 90°
Question 3. Sides AD and AB of a cyclic quadrilateral ABCD beside are produced to the points E and F respectively. If <CBF = 120°, let us write by calculating the value of CDE.
Solution:
Given
Sides AD and AB of a cyclic quadrilateral ABCD beside are produced to the points E and F respectively. If <CBF = 120°
In the figure, ∠BAD= ∠CBF=120º
∠CDE = 180º-120º
= 60º
The value of CDE = 60º
Question 4. ABCD is a cyclic quadrilateral. Sides AB and DC, when produced, meet at point Q. If ZADC = 85° and BPC = 40°, let us write by calculating the value of ZBAD and COD.
Solution:
Given
ABCD is a cyclic quadrilateral. Sides AB and DC, when produced, meet at point Q. If ZADC = 85° and BPC = 40°,
For cyclic quadrilateral ABCD,
exterior ∠PBC = ∠ADC = 85°
∴ In ΔBPC, ∠BCP = 180° – (85° + 40°) = 55°
Again, ∠BAD = exterior∠BCP = 55°
∴ In ΔCQD, ∠CQD + ∠DCQ = 85°
∴ ∠CQD = 85° – ∠DCQ
= 85° – ∠BCP
= 55°
∴ ∠BAD = 55°
and ∠CQD = 30°
Again, ∠BAD = exterior ∠BCP = 55°
∴ In ΔCQD, ∠CQD + ∠DCQ = 85°
∴ ∠CQD = 85° – ZDCQ
= 85° – ∠BCP
= 55°
∴ ∠BAD = 55°
and ∠CQD = 30°
Question 5. Let us prove that a cyclic parallelogram is a rectangular
Solution :
Given: ABCD is a cyclic parallelogram.
To prove: Quadrilateral ABCD is a rectangular picture.
Proof: ABCD is a parallelogram.
∴∠ABC =∠ADC
Again, ABCD is a cyclic quadrilateral.
∴ ∠ABC + ∠ADC = 180°
So, 2∠ABC= 180°.
∴ ∠ABC = 90°
One angle of the parallelogram is a right angle. So, ABCD is a rectangular picture.
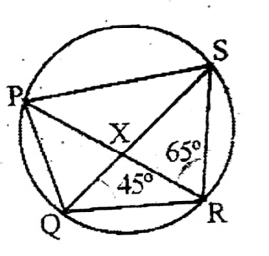
Question 6. In the picture beside two diagonals of quadrilateral PQRS in- intersect each other at point X in such a way that PRS = 65° and ZRQS = 45°. Let us write by calculating the value of SQP and ZRSP.
Solution:
Given
In the picture beside two diagonals of quadrilateral PQRS in- intersect each other at point X in such a way that PRS = 65° and ZRQS = 45°.
∠SQP = ∠PRS = 65° (on the same segment)
∠RPS = ∠RQS = 40° (on the same segment)
∠RSP = 180° – (65° +45°)
= 180° – 110°
= 70°
Question 7. Side AB of a cyclic quadrilateral ABCD is produced to the point X and by measuring we see that XBC= 82° and ∠ADB = 47°. Let us write by measuring the value of <BAC.
Solution:
Given
Side AB of a cyclic quadrilateral ABCD is produced to the point X and by measuring we see that XBC= 82° and ∠ADB = 47°.
Find ∠BAC.
As ABCD is a cyclic quadrilateral.
.. ∠ADC + ∠ABC = 2 rt. angles
Again, ∠ABC +∠XBC= 2 rt. angle
.. ∠ADC + ∠ABC = ∠ABC + <XBC
∠ADC = ∠XBC = 80° (given)
.. ∠BDC + ∠BDA = ∠ADC
∠BDC + 47° = 80° [∠BDA = 47° (given)]
.. ∠BDC = 82°-470°
= 35°
.. ∠BDC & ∠BAC are in the same segment.
.. <BAC = ∠BDC = 35°
.. <BAC 35°
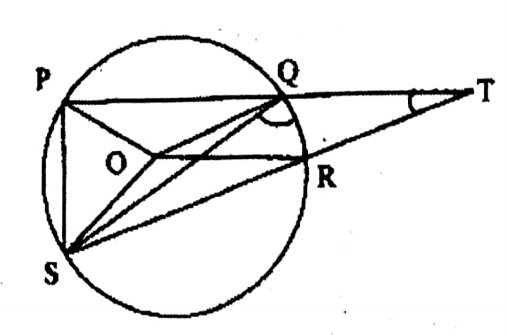
Question 8. Two sides PQ and SR of a cyclic quadrilateral PQRS are produced to meet at the point T. O is the centre of the circle. If ∠POQ = 110°,∠QOR = 60°, and ∠ROS = 80°, let us write by measuring ∠RQS and ∠OTR.
Solution:
Given
Two sides PQ and SR of a cyclic quadrilateral PQRS are produced to meet at the point T. O is the centre of the circle. If ∠POQ = 110°,∠QOR = 60°, and ∠ROS = 80°,
PQ & RS, the two sides of the cyclic quadrilateral, meet at T, when produced.
O is the centre of the circle.
∠POQ=110°,
∠QOR = 60°,
& ∠ROS = 80°
To find ∠RQS &∠QTR.
On the same segment SR, ∠RQS is the angle on the circumference &
∠ROS =1/2
∠ROS =1/2 x 80° = 40°
.. We know, ∠POQ + ∠QOR + ∠ROS + ∠SOP = 360°
..∠SOP= 360° – (∠POQ+ ∠QOR + ∠ROS)
= 360°-(110° +60° +80°)
= 360° – 250°
= 110°
or, ∠SOP = 110°,
∠PQR = ∠PQS + ∠SQR
= 55° + 40° = 95°
.. ∠PQR + ∠RQT = 180°
∠RQT 180° – ∠PQR 180° – 95° = 85°
In ΔQOR, OQ = OR (same radiii)
∴ ∠OQR = OR
Again, ∠OQR + ∠ORQ+∠QOR = 180°
or, 2∠OQR +60° = 180°
∠OQR = 1/2 (180° 60°) 60° = ∠ORQ
Again, In ΔORS, OR = OS (same radii)
∴ ∠ORS = ∠OSR
∠ORS + ∠OSR +∠SOR= 180°
2∠ORS+80° = 180°
∠ORS = ∠OSR =1/2(180° 80°)= 50°
∠SRQ = ∠ORS + ∠ORQ = 50° + 60° = 110°
∠QRT = 180°-∠SRQ
= 180°-110°-70°
In ΔQTR, ∠QTR + ∠QRT+ ∠RQT = 180°
∠QTR = 180° (∠QRT + ∠RQT)
= 180° (70° 85°) = 25°
∴ ∠RQS = 40° &∠QTR = 25°
Question 9. Two circles intersect each other at points P and Q. Two straight lines through points P and Q intersect one circle at points A and C respectively and the other circle at points B and O respectively. Let us prove that AC || BD.
Solution:
Given
Two circles intersect each other at points P and Q. Two straight lines through points P and Q intersect one circle at points A and C respectively and the other circle at points B and O respectively.
To prove AC || BD.
Join A, C; B, D & P, Q.
Proof ACQP is a cyclic quadrilateral.
:. ∠PAC + ∠PQC = 2 rt. angles
Again, PQ meets CD at Q
∴∠PAC+ ∠PQD = 2 rt. angles
∴ ∠PAC + ∠PQC =∠PQC +∠PQD
∠PAC = ∠PQD
As PQDB is a cyclic quadrilateral.
∴ ∠PBD + ∠PQD = 2 rt. angles
or, ∠PBD +∠PAC = 2 rt. angles (∠PQD = ∠PAC)
.. AB cuts AC & BD, and the sum of the internal angles of the same sides of the intercepts is equal to two right angles.
.. AC || BD
Question 10. I drew a cyclic quadrilateral AQCD and the side BC is produced to point E. Let us prove that the bisectors of ∠BAD and ∠DCE meet in the circle.
Solution: ABCD is a cyclic quadrilateral.
Side BC is produced to E & the bisector of ∠BAD cuts the circle at F.
Join C, F.
To prove, CF straight line bisects DCE.
Proof: DCF & ∠DAF are in the same segment.
∴ ∠DCF = ZDAF
AF bisects ∠BAD.
∴ ∠DAF = 1/2 ZBAD
∴ ∠DCF =∠DAF = ∠BAD———(1)
ABCD is a cyclic quadrilateral.
∴ ∠BAD + 2BCD = 2 rt. angles ——-(2)
BE meets DC at C.
∴ ∠DCE + ∠BCD = 2 rt. Angles ——(3)
From (2) & (3),
∠BAD + ∠BCD = ∠DCE + ∠BCD
or ∠BAD = ∠DCE ———-(4)
∴ ∠DCE= 2∠DCF
∴CF is the bisector of ∠DCE.
Question 11. Mohit drew two straight lines through any point X exterior to a circle to intersect the circle at points A, B, and points C, D respectively. Let us prove logically that ΔXAC and ΔXBD are equiangular.
Solution:
Given
Mohit drew two straight lines through any point X exterior to a circle to intersect the circle at points A, B, and points C, D respectively.
From an external point X, two straight lines are drawn, which cut the circle at A, B, and C, D.
To prove that two angles of each of the ΔXAC & ΔXBD are equal.
i.e., ΔXAC & ΔXBD are equiangular.
Join A, C & B, D.
ABCD is a cyclic quadrilateral
∴ ∠ABD + ∠ACD = 2 rt. angles——-(1)
AC meets DX at C
∴ ∠ACD + ∠ACX 2 rt. angles———–(2)
∠ABD+∠ACD = ∠ACD +∠ACX
∠ABD = ∠ACX = <XBC
Again, as ΔBCD is a cyclic quadrilateral,
∠BDC + <BAC = 2 rt. angles
& ∠BAC + ∠CAX = 2 rt. angles.
∠BDC + ∠BAC = ∠BAC + ∠CAX .
∠BDC=∠CAX or, ∠BDX = <CAX
Now, in Δ XAC & ΔXBD,
∠XCA = ∠XBD;
∠XAC = <BDX
& ∠AXC = ∠BXD (Same angle)
∴ΔXAC & ∴XBD are equiangular.
Question 12. I drew two circles that intersect each other at points G and H. Now I drew a straight line through point G which intersects two circles at points P and Q and the straight line through point H parallel to PQ intersects the two circles at points R and S. Let us prove that PQ = RS.
Solution: Two circles intersect each other at G & H. A straight line passing through G cuts the circles at P & Q.
And a straight line passing through H cuts the circles at R & S. To prove PQ = RS.
Join P, R; G, H & Q, S.
PRHG is a cyclic quadrilateral.
∴ ∠RPG + ∠RHG = 2 rt. angles.
Again, GH meets RS at H.
∴ ∠RHG + ∠GHS = 2 rt. angles
∴ ∠RPG+∠RHG = ∠RHG + ∠GHS
∴ ∠RPG = ∠GHS——–(1)
Again, as GHSQ is a cyclic quadrilateral.
∴ ∠GQS+ ∠GHS = 2 rt. angles.
and ∠GHS + ∠GHR = 2 rt. angles.
∠GQS +∠GHS = ∠GHS + ∠GHR
∠GQS = ∠GHR——(2)
Adding (1) & (2).
<RPG + ∠GQS = <GHS + ∠GHR
or, ∠RPG+∠GQS = 2 rt. angles
i.e., straight line PQ cuts PR & QS, & the sum of the internal angles on the same side of the intercept are equal to 2 rt. angles.
.. PR || QS & PQ || RS (given).
PQSR is a parallelogram.
.. PQRS Proved.
Question 13. I drew a triangle ABC of which AB = AC and E is any point on BC produced. If the circumcircle of ABC intersects AE at point D. Let us prove that ∠ACD =∠AEC.
Solution: In AABC, AB = AC, E is a point on produced BC.
AE cuts the circumcircle of AABC at D.
To prove, ∠ACD = ∠AEC
Join C,D.
Proof: ABCD is a cyclic quadrilateral.
∠ABC + ∠ADC = 2 rt. angles.
Again, straight-line CD meets AE at D.
∴ ∠ADC + ∠CDE = 2 rt. angles.
∴ ∠ABC + ∠ADC= ∠ADC + ∠CDE
∴ ∠ABC = CDE
In ΔABC, AB = AC,
∴ ∠ABC = ∠ACB
∴∠ACB = ∠CDE
Again, side EC of CDE is produced.
External vDCB = ∠CDE+∠CED
or, ∠ACB+∠ACD = ∠CDE + ∠AEC
or, ∠CDE+∠ACD = ∠CDE + ∠AEC [ ∠ACD = ∠CDE]
∴∠ACD = ∠AEC. Proved.
Question 14. ABCD is a cyclic quadrilateral. Chord DE is the external bisector of BDC. Let us prove that AE (or produced AE) is the external bisector of <BAC.
Solution: ABCD is a cyclic quadrilateral, and chord DE is the extra
To prove, AE (or produced AE) is the external bisector of <BAC.
Proof: DE is the external bisector of ∠BDC.
∴ ∠AED = ∠ACD = ∠ABC (angles on the same segment)
Again, <BAC = ∠BDC (angles on the same segment) [as DE is A ∠BDC]
.. AE is the external bisector of BAC.
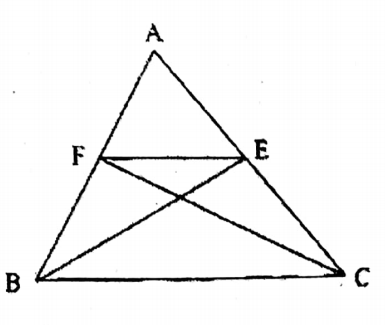
Question 15. BE and CF are perpendicular on sides AC and AB of t Let us prove that four points B, C, E, and F are on the same circle
Solution: InΔABC, BE & CF are two perpendiculars on the side To prove points B, C, E, and F are on the same circle.
That prove also AAEF & AABC are equiangular.
Join E, F.
Proof: AS 1 BE 1 AC & CF 1 AB
∴ ∠BEC = 1 rt angle & ZBFC = 1 rt. angle
∴ BEC = ∠BFC = 1 rt. angle
∴Points B, C, E, and F are on the same circle.
Now, inΔAEF &ΔABC,
∠FAE=∠BAC (Same angle)
Question 16. ABCD is parallelogram. A circle passing through points A and B intersects the sides AD and BC at points E and F respectively. Let us prove that the four points E, F, C, and D are concyclic.
Solution: ABCD is a parallelogram.
A circle passing through points A & B intersects the sides AB & BC at E & F respectively.
To prove that the points E, F, C, and D are concyclic.
Join E, F.
Proof: ABCD is a parallelogram.
∴ ∠BAD + ∠ADC = 2 rt. angles.
Again, ABEF is a cyclic quadrilateral.
∠BAE+∠BFE = 2 rt. angles
∴ ∠EFC =∠BAE
∠EFC = <BAD
But∠BFE+∠CFE = 2 rt. angles.
∴∠EFC + ∠ADC = 2 rt. angles.
∠EFC + ∠EDC = 2 rt. angles.
∴∠EFCD is a cyclic quadrilateral.
.. Points E, F, C,D are concyclic
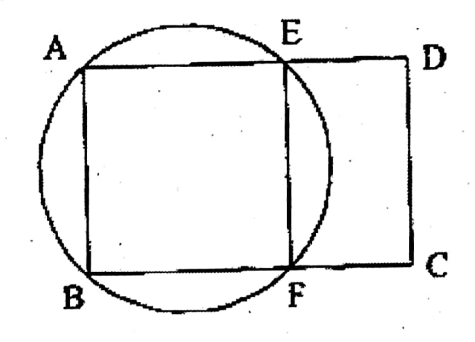
Question 17. ABCD is a cyclic quadrilateral. The two sides AB and DC are produced to meet at point P and the two sides AD and BC are produced to meet at point R. The two circumcircles of ABCP and ACDR intersect at point T. Let us prove that the points P, T, and R are collinear.
Solution: To prove that points P, T, and R is collinear.
Joint P, T;
T, R & C, T.
In BCP & ADP,
∠BPC = ∠APD; ∠PBC =∠ADP
& ∠BCP = ∠PAD
∴ΔBCP & ΔAPD are equiangular.
i.e., they are similar.
Now, in ΔPCT & ΔRCT,
∠PCT = ∠CRT,
CT common & ∠RCT = ∠TPC
∴ΔPCT ≅ ΔRCT
∴<PTC =∠RTC (corresponding angle)
As CT is the common side of∠PTC & ∠RTC
∴TR & TP are on the same straight line.
∴ P, T, and R are collinear.
Question 18. If point O is the ortho of triangle ABG, let us prove that it is the incentre of ΔDEF.
Solution: To prove O is the incentre of the ΔDEF.
In ΔBDO & ΔAEO.
∠BOD = ∠AOE, ∠BDO = ∠AEO = 90°
& Rest ∠BDO = Rest ∠EAO
ΔBDO ≅ ΔΑΕΟ,
∴ OD = OE
Similarly, ΔBOD ≅ ΔAFO
∴ OD = OF
∴ OD =OE = OF
∴ O is the incentre of the ΔDEF.
Question 19. I drew a cyclic quadrilateral ABCD such that AC bisected <BAD. Now produced AD to a point E is such a way that DE AB. Let us prove that CE = CA.
Solution: To prove CE = CA
Join B, D.
Proof: Diagonal AC bisects ZBAD.
∴<BAC = ∠DAC
Again, ∠DBC= <DAC
As these angles are on the same segment DC,
Again, ∠BDC= <BAC
As on the same segment BC,
∴ ∠DBC= <BDC
∴ BC= DC.
Again, ∠ACD = ∠ABD
As on the same segment AD,
∴ ∠ABC = ∠ABD + ∠DBC
∠CDE = <DAC + ∠ACD
∴ ∠ABC = ∠CDE
Now, in ΔABC & ΔCED,
AB = DE (given),
BC = DC & ∠ABC = ∠CDE
∴ ABC == ΔCED (SAS)
∴ AC = CE
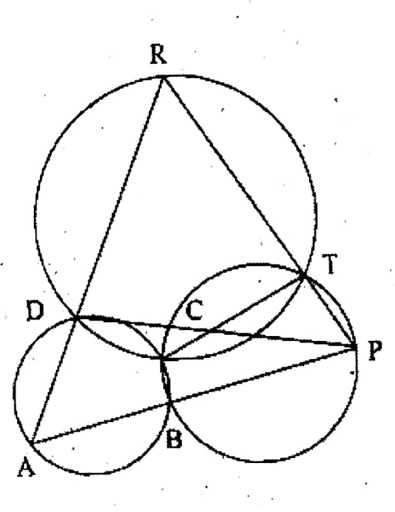
Question 20. In two circles, one circle passes through the centre Q of the other circle and the two circles meet each other at point A intersecting the circle which passes through point O at the point P and the circle with centre O at point R. Joining P, B, and R, B. Let us prove that PR = PQ.
Solution: Let the straight line PB cut the circle with centre O at point C.
Join A, C.
In ΔPRB & ΔACP
∠BPR = ∠APC (same angle)
∠PBR = ∠CAP [. ARBC is a cyclic quadrilateral]
∴ ∠PBR + ∠RAC = 2 rt. angles
= ∠RAC + ∠CAP
∴ ΔPRB + ΔACP are obtuse-angled triangles, i.e., sim
∴∠PRB = ∠PBR
∴ PB = PR Proved.
Question 21. Let us prove that any four vertices of a regular pentagon are concyclic.
Solution: Let ABCDE is a pentagon.
To prove A, B, C, and E are concyclic.
Join C, E parallel to AB.
As AB || CE
∴ ∠ABC +∠EAB = 2 rt. angles
Again,∠ABC + ∠BCE 2 rt. angles
As the sum of opposite angles of the quadrilateral ABCE is a supplement
∴ Points A, B, C, and E are concyclic.
Multiple Choice Questions Chapter 10 Theorems Related To cyclic Quadrilateral Exercise 10.1
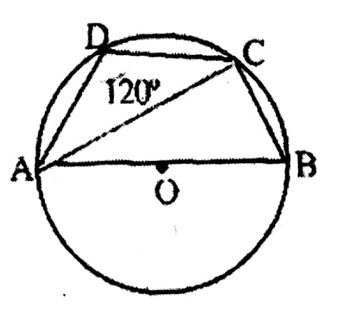
Question 1. In beside O is the centre of the circle and AB is the diameter. ABCD is a cyclic quadrilateral. <BAC is
1. 50°
2. 60°
3. 30°
4. 40°
Solution: ABC 180° = 120° = 60°
∴∠ACB = 90° (semicircle angle)
<BAC = 180° – (90° +60°)
= 180° – 150°
= 30°
Answer. 3. 30°
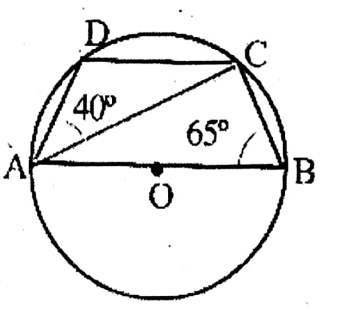
Question 2. In beside O is the centre of the circle and AB is the diameter. ABCD is a cyclic quadrilateral. The value of ∠BCD is
1. 75°
2. 105°
3. 115°
4. 80°
Solution: ∠ACB 90° (semicircle angle)
∠ADC = 180° – 65°
= 115°
∠ACD = 180° – (115° 40°)
=180° – 155°
= 25°
∠BCD = (90° +25°)
= 115°
Answer. 3. 115°
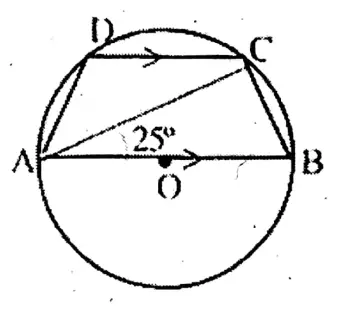
Question 3. In beside O is the centre of the circle and AB is the diameter. ABCD is a cyclic quadrilateral in which AB || DC and if BAC = 25° then the value of <DAC is
1. 50°
2. 25°
3. 130°
4. 40°
Solution: ∠ACB = 90° (semicircle angle)
∴∠ABC = 180° – (90° +25°)
= 180° – 115°
= 65°
∠DCA alternate ∠CAB = 25°
∠ADC = 180° – 65°
= 115°
∠DAC = 180° – (115° +25°)
= 180° – 140°
= 40°
Answer. 4. 40°
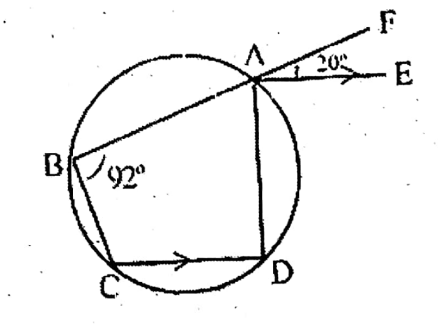
Question 4. Besides ABCD is a cyclic quadrilateral. BA is produced to the point F. If AE || CD, ∠ABC= 92° and FAE = 20°, then the value of ∠BCD is
1. 20°
2. 88°
3. 108°
4. 72°
Solution:∠ADC = 180° – 92°
= 88°
∠DAF = ADC = 88° [AE || CD]
∠DAE = 88° + 20°
= 108°
∠BAD = 180° – 108°
= 72°
∠BCD = 180° – 72°
= 108°
Answer. 3.108°
Question 5. Besides two circles intersect each other at points C and D. Two straight lines through points D and C intersect one circle at points E and F respectively. If DAB = 75°, then the value of DEF is
1. 75°
2. 70°
3. 60°
4. 105°
Solution: Join D, C.
ZDCF = ZBAD = 75°
ZDEF = 180°- 75°
= 105°
Answer. 4. 105°
Chapter 10 Theorems Related To cyclic Quadrilateral Exercise 10.1 True Or False
1. The opposite angles of a cyclic quadrilateral are complementary.
False
2. If any side of a cyclic quadrilateral is produced, the exterior angle so formed is equal to the interior opposite angle.
True
Chapter 10 Theorems Related To cyclic Quadrilateral Exercise 10.1 Fill In The Blanks
1. If the opposite angles of a quadrilateral are supplementary then the vertices of the quadrilateral will be Concyclic.
2. A cyclic parallelogram is a Rectangle.
3. The vertices of a cyclic square are Concyclic.
Chapter 10 Theorems Related To cyclic Quadrilateral Exercise 10.1 Short Answer
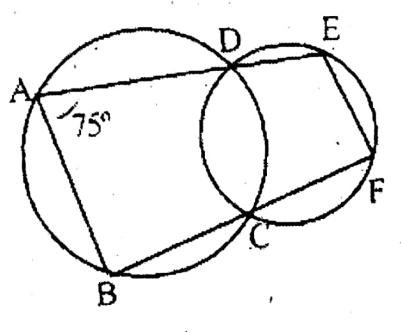
Question 1. In the beside two circles with centres P are Q intersect each other at points B and C. ACD is a line segment. If ∠ARB = 150°, ZBQD = x°, then let us find the value of x.
Solution:
In the beside two circles with centres P are Q intersect each other at points B and C. ACD is a line segment. If ∠ARB = 150°, ZBQD = x°
BCD 150°
.. Reflex ∠BQD = 2 x 150°
= 300°
.. x° = zBQD
= 360° – 300°
= 60°
.. x = 60°
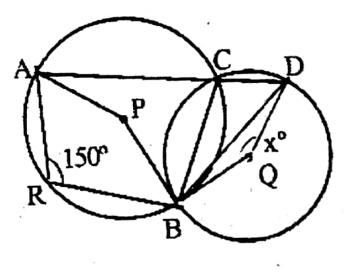
Question 2. In the beside two circles intersect at the points P and Q. If∠QAD = 80° and PDA = 84°, then let us find the value of ∠QBC and BCP.
Solution.
In the beside two circles intersect at the points P and Q. If∠QAD = 80° and PDA = 84°,
∠QPC = <DAQ = 80°
∠QBC 180° – 80° = 100°
∠PQB = ∠ADP = 84°
∠BCP = ∠AQD = 180° – (100° + 60°)
= 20°
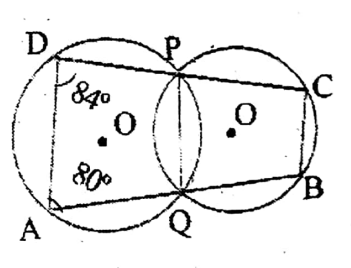
Question 3. If ∠BAD = 60°, ∠ABC = 80°, then let us find the value of ∠DPC and ∠BQC.
Solution. ∠ADQ = ∠ADC= 180° 80° = 100°
∠DPC = ∠APB
= 180° – (80° +60°)
= 40°
∠BQC = ∠AQD
=180° – (100° + 60°)
= 20°
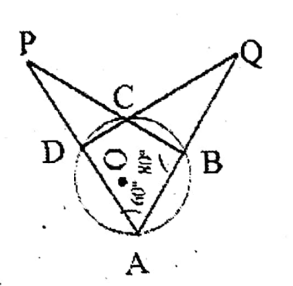
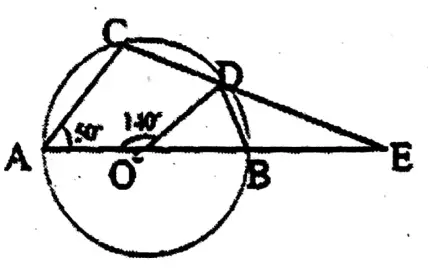
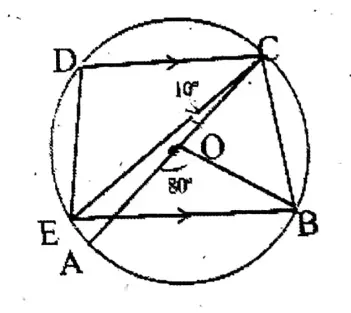
Question 4. In beside O is the centre of the circle and AC is its diameter. If∠AOD = 140° and CAB = 50°, let us find the value of BED.
Solution. ∠BOC =180° – 80° =100°
<BEC = 1/2 <BOC = 1/2 x 100° = 50°
.. OB = OC
∠OCB =∠OBC = 180°-100°/2
= 80°/2
= 40°
∠BCF =(40° + 10°) = 50°
.. BED (50° + 50°) = 100°
Question 5. Beside O is the centre of the circle and AB is its diameter. If∠AOD = 140° and CAD = 50°, let us find the value of ∠BED.
Solution. ∠BOD = 180°-140°
= 40°
.. OB = OD
∠OBD = ∠ODB = 140°/2
= 70°
∠DBE = 180°-70°
= 110°
∠ACF = 180°-70°
= 110°
∠BED = ∠AEC = 180° – (110° +50°)
= 180° – 60°
=20°
