WBBSE Solutions For Class 10 Maths Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.1

Maths WBBSE Class 10 Solutions Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.1

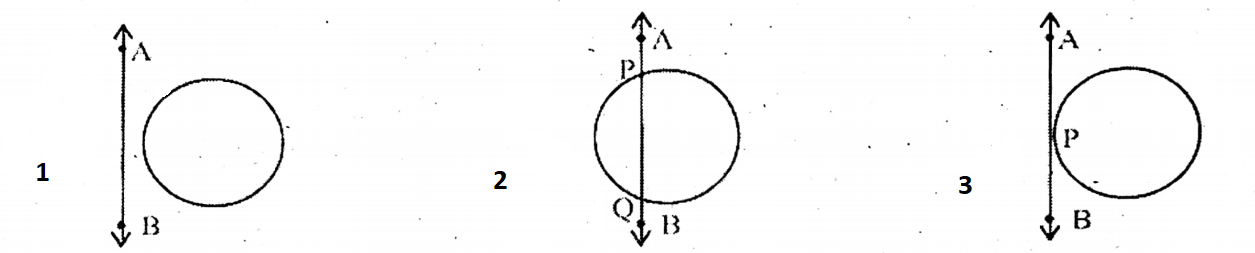
Question 1. But in no. 3 in what position are the stick AB and the circular ring? 

Solution: The stick AB touches the circular ring at point P. Like me, my friend Sumedha similarly drew in what positions a straight line and a circular ring can be to each other in her copy. We see, in picture no. 1 straight line AB does not intersect the circle. Again, in picture no. 2 the straight line AB intersects the circle at points P and Q.

Read and Learn More WBBSE Solutions For Class 10 Maths

Question 2. But in pictures no. 2 and 3 what is this straight line AB of the circle called? 

Solution: In picture no. 2 AB is a secant of a circle and PQ is a corresponding chord of secant AB. We see that in picture no 3 the common point of circle and straight line AB is P.

∴ The straight line AB touches the circle at point P.

Question 3. But in picture no. 3 what is the straight line AB of the circle called?

Solution: In picture no. 3 the straight line AB of the circle is called a tangent.

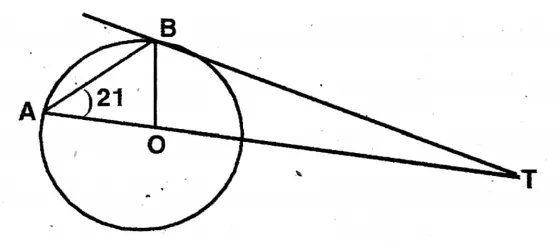
Question 4. Masum has drawn a circle with a center ‘O’, of which AB is a chord. I draw a tangent at point B which intersects extended AO at point T. If ∠BAT = 21°, let us write by calculating the value of BTA.

Solution:

Given

Masum has drawn a circle with a center ‘O’, of which AB is a chord. I draw a tangent at point B which intersects extended AO at point T. If ∠BAT = 21°,

∠TOB = ∠BAT + ∠ABO

=2∠BAT = 42°

Again in ΔBOT, ∠OBT = 90°

∴∠BTO = 180° (∠TOB + ∠OBT)

180°- (90° 42°) = 38°

The value of BTA = 38°

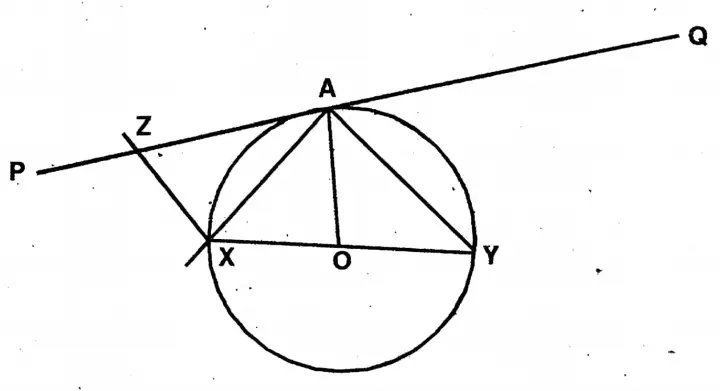
Question 5. XY is a diameter of a circle. PAQ is tangent to the circle at the point ‘A’ lying on the circumference. The perpendicular drawn on the tangent of the circle from X intersects PAQ at Z. Let us prove that XY is a bisector of ∠YXZ.

Solution:

Given

XY is a diameter of a circle. PAQ is tangent to the circle at the point ‘A’ lying on the circumference. The perpendicular drawn on the tangent of the circle from X intersects PAQ at Z.

Let O is the center of the circle.

Joint A, O as PAQ is a tangent. 

∴∠OAZ = 90°

Again, ∠OAZ = ∠OAX + ∠AZX     [AOAX isosceles Δ ]

∠OAX = ∠OXA 

∴ 90° =  ∠OXA + ∠ZAX

& 90° =  ∠ZAX + ∠ZXA

∴ ∠OXA + ∠ZAX = ∠ZAX + ∠ZXA

or, ∠OXA = ∠ZXA

∴ XA is the bisector of ∠YXZ.

Question 5. I drew a circle having PR as a diameter. I draw a tangent at point P and point S is taken on the tangent of the circle in such a way that PR = PS. If RS intersects the circle at point T, let us prove that ST = RT = PT.

Solution:

Given

I drew a circle having PR as a diameter. I draw a tangent at point P and point S is taken on the tangent of the circle in such a way that PR = PS. If RS intersects the circle at point T

As ∠PTR is a semicircle angle.

∴ ∠PTR = ∠TSP + ∠TPS

Again, 90° = ∠TSP + ∠RPT

∴∠TSP =∠RPT

1 TSP = ZRPT; 

2 PR PS & 

3 PT is common.

.. APTS == APTR

.. ST = PT Proved.

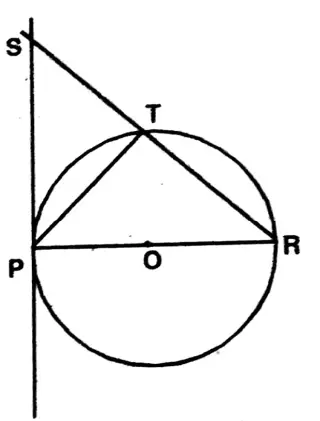
Question 6. Two radii OA and OB of a circle with center O are perpendicular to each other. If two tangents drawn at the points A and B intersect each other at point T, let us prove that AB = OT and they bisect each other at a right angle.

Solution:

Given

Two radii OA and OB of a circle with center O are perpendicular to each other. If two tangents drawn at the points A and B intersect each other at point T

Let O be the center of the circle.

In quadrilateral ΔOBT, AO = OB

& ∠AOB = ∠TAO = ∠TBO = 90°

∴ ΔOBT is a square.

∴ Diagonal AB = OT.

They bisect each other perpendicularly.

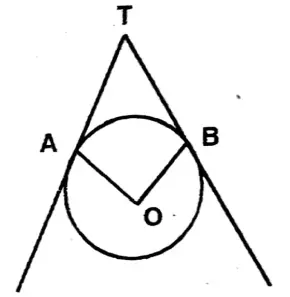
Question 7. Two chords AB and AC of the larger of two concentric circles touch the other circle at points P and Q respectively. Let us prove that PQ = 1/2 BC

Solution:

Given

Two chords AB and AC of the larger of two concentric circles touch the other circle at points P and Q respectively.

Let O be the center of two concentric circles. 

AB & AC the two chords of the big circle are the tangents of the small circles. 

Join A, O; B, O; C, O.

∴ AO = CO (Radius)

Again, OQ ⊥ AC

∴ AQ = QC.

Similarly, AP = PB.

∴ In ΔABC, P & Q are the midpoints of AB & AC.

∴ PQ = 1/2 BC.

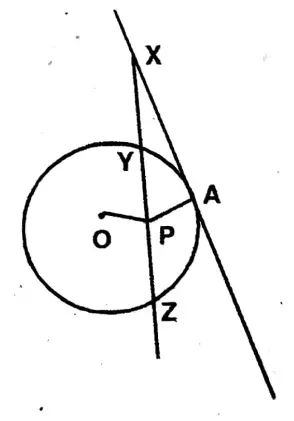
Question 8. X is a point on the tangent at the point A lies on a circle with center O. A secant drawn from a point X intersects the circle at the points Y and Z. If P is a mid-point of YZ, let us prove that XAPO or XAOP is a cyclic quadrilateral.

Solution:

Given

X is a point on the tangent at the point A lies on a circle with center O. A secant drawn from a point X intersects the circle at the points Y and Z. If P is a mid-point of YZ,

YZ is a chord of the circle. P is the midpoint of YZ.

∴ OP ⊥ YZ

Again, XA is a tangent at A.

∴ AO ⊥ XY.

∴ In the Quadrilateral XAPO,

∠OAX & ∠XPO are equal = 90°

∴ XAPO is a cyclic quadrilateral whose XO is a diameter.

Question 9. P is any point on the diameter of a circle with center O. A perpendicular drawn on diameter at the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R. A tangent drawn at the point R intersects extended OP at the point S. Let us prove that SP = SR.

Solution:

Given:

P is any point on the diameter of a circle with center O. A perpendicular drawn on diameter at the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R. A tangent drawn at the point R intersects extended OP at the point S.

∠ORP + <PRS = 90°

or, ∠OQP+∠QQP = 90°

∴ ∠ORP = ∠OQP [as OQ = OR]

∴ ∠PRS = ∠QQP—–(1)

∴∠OPQ = ∠SPR——–(2) (Vertically opposite)

Again, ∠OPQ + ∠OQP = 90°

& ∠OQP+ ∠PQQ, = 90°

:. ∠OPQ = ∠PQQ,

∴ ∠SPR = ∠PRS

∴ Aln SPR, SP = SR Proved.

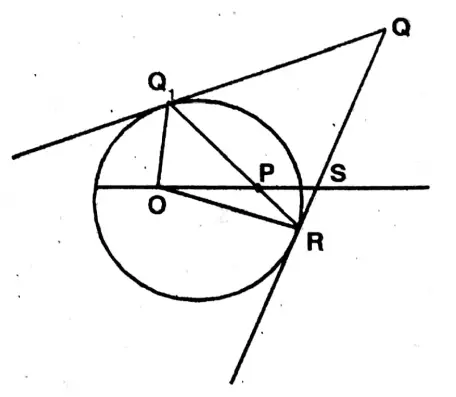
Question 10. Rumela drew a circle with center O, of which QR is a chord. Two tangents drawn at points Q and R intersect each other at point P. If QM is a diameter, let us prove that ZQPR = 2 ZRQM.

Solution:

Given

Rumela drew a circle with center O, of which QR is a chord. Two tangents drawn at points Q and R intersect each other at point P. If QM is a diameter

In Quadrilateral PQOR, ∠PQO = ∠PRO = 90°

∴ Opposite angles of the Quadrilateral PQOR are supplementary.

∴ PQOR is a cyclic quadrilateral whose ∠ORP = 90°. 

∴ PQOR is a square (OQ = OR).

∴∠ROQ 90° = ∠QPR.

& Aln QOR, OQ = OR.

∴∠RQM = 45°

∴ ∠OPR – 2 ∠RQM. Proved.

Question 11. Two chords AC and BD of a circle intersect each other at point O. If two tangents drawn at points A and B intersect each other at the point P and two tangents drawn at points C and D intersect at the point Q, let us prove that ZP + ZQ = 22BOC.

Solution:

Given

Two chords AC and BD of a circle intersect each other at point O. If two tangents drawn at points A and B intersect each other at point P and two tangents drawn at points C and D intersect at point Q

Let ‘R’ be the center.

∴ ΔRBP is a cyclic quadrilateral.

∴ ∠A + ∠B 180°

∴ ∠ARB + ∠P = 180°

∴ ∠ARB = 2∠ACB

∴ 2∠ARB + P = 180°——(1)

Similarly, 2∠DAO + ∠Q = 180°

or, 2∠CBO + ∠Q = 180°——-(2)

∴ 2∠ACB + 2∠CBO + ∠P + Q = 360°

Adding (1) & (2),

<P+Q = 2 [180 – (∠ACB + <CBO)]

∴∠P + ∠Q = 2∠BOC.

1. We take three colored cardboard.

2. Drawing three circles with the same measures with center O on white paper cut off the circular region and paste them on this colored paper.

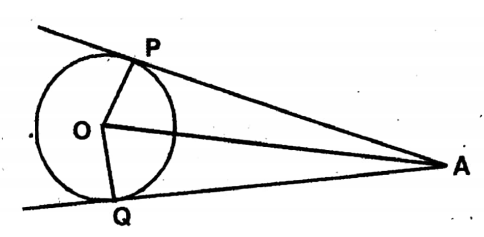
Solution: We see that in picture no. 1, i.e., two tangents can be drawn to a circle from any point outside it.

In no: 2 i.e., one tangent can be drawn to a circle from a point lying on the circle.
We understand that, from any     [interior/external] point, no tangent can be drawn to the circle.

Answer. Interior.

WBBSE Solutions Guide Class 10

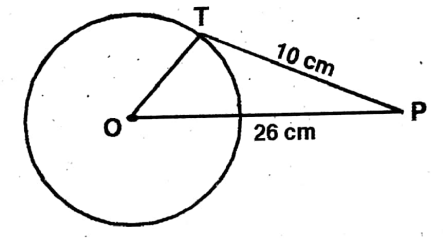
Application 1. If I draw a circle with center O, point P is 26 cm. away from the center of the circle and the length of the tangent drawn from point P to the circle is. 10 cm, let us write by calculating the length of the radius of the circle.

Solution:

Given

If I draw a circle with center O, point P is 26 cm. away from the center of the circle and the length of the tangent drawn from point P to the circle is. 10 cm,

PT = 10 cm., PO= 26 cm.

From right-angle triangle POT, we get,

PO² = PT²+ OT² [we get from Pythagoras theorem]

.. (26cm)² (10cm)² + PT²

or, OT² (26cm)²- (10cm)²= 576 cm.

.. OT = 24 cm.

The length of the radius of the circle = 24 cm.

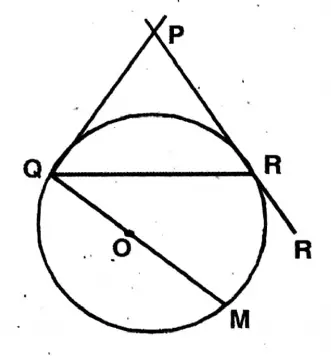
Question 12. Let us prove that the line segment joining a point outside a circle and the center bisects the angle included by two tangents drawn from the external point.

Solution: O is the center of the circle and two tangents PA & PB are drawn from the external point P.

Join O,A & O,B; O,P

In ΔAOP & ΔBOP

OA = OB; OP common

& ∠OAP ∠OBP common

∴ΔΟΑΡ ≅ ΔΟΒΡ

∴ ∠APO

∴∠BPO.

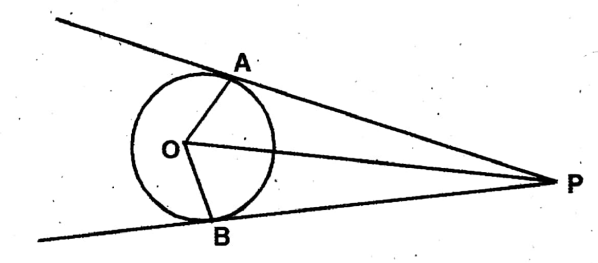
Question 13. Let us prove that the bisector of an angle includes two tangents to a circle from a point outside it passes through the center.

Solution: Let O be the center of the circle and two tangents PA & PB are drawn from the external point P.

Join O, A, O, B & A, B.

PD, the bisector of ∠P, cuts AB at D.

∠OAP = ∠OBP = 90°

or, ∠OAD + ∠DAP = ∠OBD + ∠DBP

∠DAP = DBP

Now in ΔABD & ΔBPD,

1 ∠APD = ∠BPD, 

2 ∠DAP = ∠DBP

3 DP is common

∴ ΔAPD ≅ ΔBPD

∴ AD – BD & ∠ADP = BDP = 90°

Again, inΔOAD & ΔOBD, 

1 OA = OB; 

2 ∠OAD = ∠OBD; 

3 AD = BD. 

∴ΔOAD ≅ ΔOBD

∴ ∠ODA = ∠ODB = 90°

∴ AB ⊥OD & AB ⊥ PD

∴ Produced PD will pass through the center. Proved.

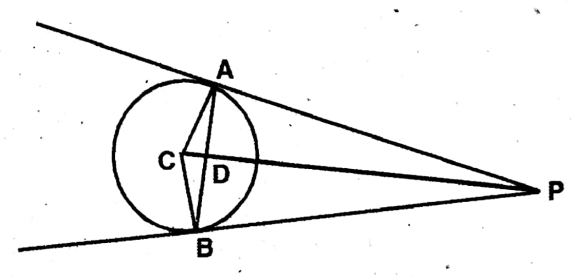
Question 14. Let us prove that if two tangents drawn to a circle at two points it intersect each other, then the lengths of the line segments from the point of intersection to the points of contact are equal.

Solution: Let P & Q be two points on a circle with center O. 

Two tangents drawn at P & Q intersect each other at A. 

To prove AP = AQ.

Joint O, P, O, Q & O, R In AAOQ & AAOP,

1 OP = OQ; OA common & ZAPO = ZBQP = 90° 

∴ ΔAOP ≅ ΔAOQ

∴ AP = AQ Proved.

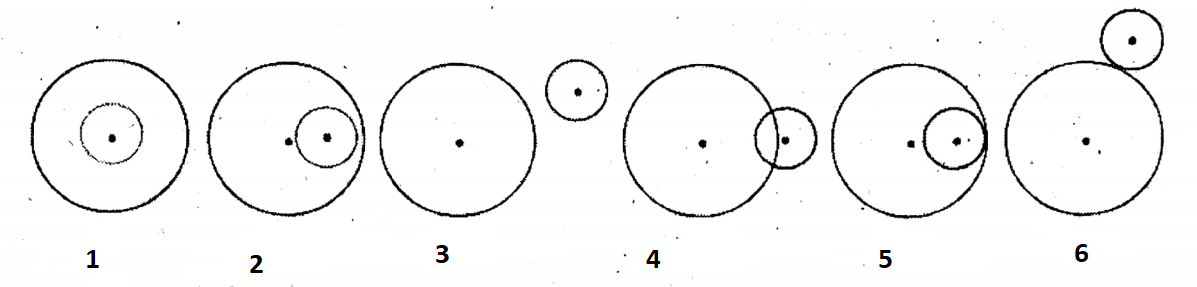
Question 15. I see the position of circular rings as being put by Rabeya and let us see the different positions of rings.

Solution: We see that in picture no. 1 two circles are concentric but in picture no. 2 two circles are not concentric, in picture no. 3 two circles do not intersect each other, in picture no. 4 the two circles intersect each other at two points.

Question 16. How shall we understand that two circles touch each other?

Solution: There is only one intersecting point P. of two circles with center O and O’s in the same plane and if the tangent of a circle with center O touches the circle with center O’ at that point, then it is called the two circles touch each other at the point P. In picture no. 7 two circles do not touch each other.

In picture no. 7 and 9 two circles touch each other. In picture no. 7 two circles touch internally each other at the point P. AB is a common tangent of two circles. Again, in picture no. 9 two circles touch externally each other at point P. AB is a common tangent of the two circles.

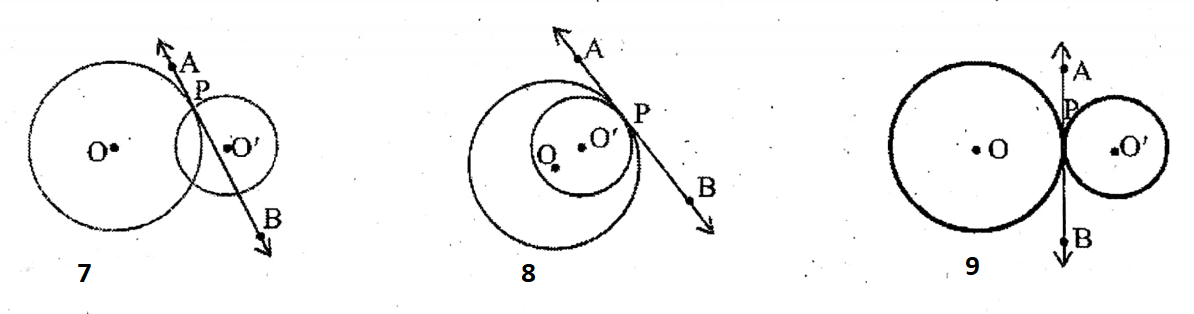
Question 17. But sometimes we see that the two circles are situated on the same side of the common tangents, again other times the two circles are situated on the opposite sides of the common tangents. What is this type of tangent called?

Solution: If two circles lie on the same side of a common tangent the tangent, is said to be a direct common tangent and if two circles lie on the opposite sides of a common tangent, the common tangent is said to be a transverse common tangent. We understand that the tangents of pictures no. 10 and 11 are direct common tangents. But in picture no. 12 there are two direct common tangents and 1 transverse common tangent. Again in picture no. 13, there are two direct common tangents and two transverse common tangents.

WBBSE Solutions Guide Class 10

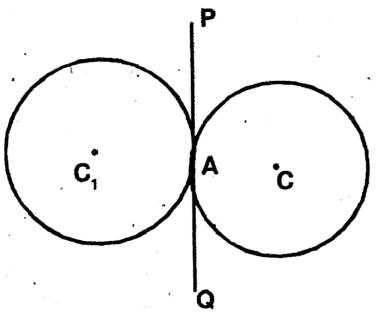
Question 18. Let us prove with the reason that if two circles touch each other, the straight line through the center of one circle and the point of constant passes through the center of another circle. 

Solution: Let two circles with centers C₁ & C₂ touch each other at A externally,

PQ is a common tangent passing through A;

Join A, C₁ & A, C₂

C₁APQ & C₂APQ

∴ PAC₁ = PA²C₂ = 90°

∴ C₁AC₂ = 180°

∴ C₁C₂ straight line, passing through A.

In the picture beside, PQ = AP + AQ.

 

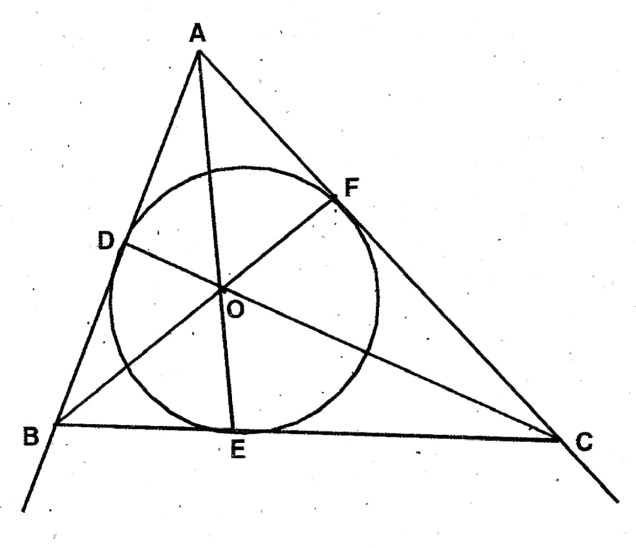
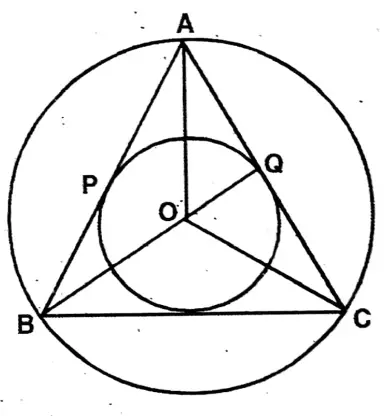
Application 1. In the adjoining figure, the incircle of AABC touches the sides AB, BC, and CA at points D, E, and F respectively. Let us prove that AD + BE + CF = AF + CE + BD = 1/2 (perimeter of AABC)

Solution:

Given

In the adjoining figure, the incircle of AABC touches the sides AB, BC, and CA at points D, E, and F respectively.

Join A, O; B, O; C, O.

In ΔBOD & ΔBOE,

1 ∠BDO = <BED

2 OD = OE (Radius)

3 OB is common

∴ ΔBOD ≅ ΔBOE,

∴ BD-BE———(1)

Similarly, from ΔCOE & ΔCOF, CE = CF———– (ii)

Similarly, from ΔAOD & ΔAOF, AF = AD—-—-(iii)

Adding (1), (2) & (3),

AD + BE + CF = AF+ CE + BD

Perimeter of AABC

= AB + BC + CA

= AD + BD + BE+ CE+ CF + AF

= 2(AD + BE + CF)

∴ AD + BE + CF = AF + CE + BD = 1/2 (AB + BC + CA)

= 1/2 of the perimeter of AABC Proved.