WBBSE Solutions For Class 10 Maths Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.2

West Bengal Board Class 10 Math Book Solution In English

Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.2

Question1. An external point is situated at a distance of 17 cm from the centre of a circle having a 16 cm diameter, let us determine the length of the tangent drawn to the circle from the external point.

Solution:

Given

An external point is situated at a distance of 17 cm from the centre of a circle having a 16 cm diameter

Let the diameter of the circle = 16 cm

∴ Radius = 16/2 

=8 cm

Distance of the external point from the centre (OP) =.17 cm

∴ In right angled ΔOAP,

AP = √OP² – OA²

=√(17)²-(8)²

= √289-64 

=√225

= 15

∴ AP 15 cm

Read and Learn More WBBSE Solutions For Class 10 Maths

 

 

Question 2. The tangents drawn at points P and Q on the circumference of a circle intersect at A. If ZPAQ is 60°, let us find the value of ZAPQ.

Solution:

Given

The tangents drawn at points P and Q on the circumference of a circle intersect at A. If ZPAQ is 60°

Let AP & AQ be two tangents to the circle with centre O.

From an external point. A.

∴ AP = AQ

ΔAPQ is an isosceles triangle.

∴ ∠APQ = ∠AQP

If ∠PAQ = 60°

∴ ∠APQ = 180°-60° / 2

= 60°

Question 3. AP and AQ are two tangents drawn from an external point A to a circle with centre O. P and Q are points of contact. If PR is a diameter, let us prove that OA || RQ. 

Solution:

Given

AP and AQ are two tangents drawn from an external point A to a circle with centre O. P and Q are points of contact. If PR is a diameter,

AP & AQ are two tangents to the circle with centre O, from an external point A. 

∴ PA = QA & ∠AOP = ∠AOQ

Now in ΔPOR & ΔQOR,

OP = OQ,  ∠POR = ∠QOR & OR is common.

∴ ΔPOR ≅ ΔQOR

PR = QR

<PRO = <QRO

OR is standing on PQ

& ∠PRO = ∠QRO

∴ QR ⊥ PQ

i.e., OA⊥OQ 

Again, PR = QR

∴ OR ⊥ RQ.

Question 4. Let us prove that for a quadrilateral circumscribed about a circle, the angles subtended by any two opposite sides at the centres are supplementary to each other. 

Solution: ‘O’ is the centre of the circle. ABCD is a quadrilateral circumscribing the circle.

Let the circle touch the sides of the quadrilateral AB, BC, CD & DA at P, Q, R, S respectively.

∴ To prove, ∠AOB +∠COD = 180° 

or ∠AOD +∠BOC = 180°

Proof: As AP & AS are two tangents of the circle from A

∴ ∠AOP = ∠AOS

Similarly, ∠BOP = ∠BOQ

∴ ∠AOB=  ∠AOP + ∠BOP = ∠AOS + ∠BOQ

Again, DS & DR are two tangents as S & R

∴ ∠DOS = <DOR

Similarly from tangents R & Q

∠COR = ∠COQ

∴ ∠COD = ∠COR+ ∠DOR= ∠COQ + ∠DOS

∴ ∠AOB + ∠COD = ∠AOS + ∠BOQ + ∠COQ + <DOS

= (∠AOS + ∠DOS) + (∠BOQ + ∠COQ)

= ∠AOD + ∠BOC.

Again, ∠AOB + ∠BOC+ ∠COD +∠DOA = 360°

 or, (∠AOB +∠COD) + (∠AOB + ∠COD) = 360°

∴ 2x (∠AOB + ∠COD) = 360°

∴ 2 x (∠AOB + ∠COD) = 360°

∴ ∠AOB + ∠COD = 360°/2 = 180°

or, 2(∠AOD + ∠BOC) = 360°

∴ ∠AOD + ∠BOC= 360°/ 2

= 180° Proved.

Question 5. Let us prove that a parallelogram circumscribed by a circle is a rhombus. 

Solution: Let O is the centre of the circle & ABCD is a parallelogram circumscribing the circle. The circle touches the parallelogram at P, Q, R & S.

Join AO, PQ, BO, QO, RO & SO.

To prove ABCD is a rhombus

Proof: AP & AS are two tangents at P & S.

∴ AP = AS & ∠AOP = ∠AOS.

Similarly, in the case of tangent BP & BQ

BP = PQ & ∠BOP =∠BOQ

Again, in the case of tangents SD & RD

SD = RD & ∠ODS = ∠ODR

Now in As BOP & BOQ,

1 ∠OPB = ∠OQB = 90°

2 ∠BOP = ∠BOQ & BP = BQ

∴ ΔBOP ≅ ΔBQO

∴ ∠PBO = ∠QBO

Similarly, from ΔDOS & ΔDOR we get ∠SDO = ∠RDO

Now, in a parallelogram ABCD, ∠ABC & ∠ADC are two opposite angles.

∴ ∠ABC = ∠ADC = ∠PBO = ∠RDO. 

Now in Δs BOP & ROD

∠BPO = ∠DRO; ∠PBO = ∠RDO & OP = OR

∴ ΔBOP ≅  ΔROD

∴ PB = DR

.. PB = SD

Now, AP + PB = AS + SD

i.e., AB = AD

∴ AB = BC = CD = DA.

∴ All the sides of the parallelogram ABCD are equal.

∴ ABCD is a rhombus.

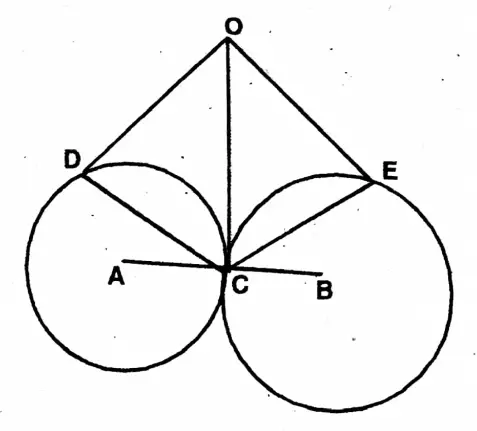
6. Two circles drawn with centres A and B touch each other externally at C. O is a point on the tangent drawn at C, OD and OE are tangents drawn to the two circles of centres A and B respectively. If ZCOD = 56°, ZCOE = 40°, ACD = x° and BCE = y°, let us prove that OD OC = OE and y – x = 8

Solution:

Given

Two circles drawn with centres A and B touch each other externally at C. O is a point on the tangent drawn at C, OD and OE are tangents drawn to the two circles of centres A and B respectively. If ZCOD = 56°, ZCOE = 40°, ACD = x° and BCE = y°

∠COD = 56°,

∠COE = 40°,

∠ACD = x°

& ∠BCE = y°

To prove OD = OC = OE & y-x=8

Proof: OD & OC are two tangents to the circle with centre A at points D and C. 

∴ OD = OC & ∠ODC = ∠OCD

Again, OD & OE are two tangents of the circle with centre B at the points C & E 

∴ OC = OE & ∠OEC = ∠OCE

∴ OD = OC = OE

∠COD = 56° & ∠COE = 40° (given)

Let ∠ACD=x° & ∠BCE = y°

∴ ∠OCD = 180°-56°/2

= 124° / 2

= 62°

OC is the common tangent of the two circles & AB

is a straight line joining the centres?

∴ OC ⊥ AB

∴ ∠OCA = ∠OCB = 90°

∠ACD=90° – ∠OCD 90° = 62°- 28°.

∴ x = 28°

Again, ∠OCE= 180°-40° / 2

= 140°/2

= 70°

∠BCE = 90° – ∠OCE = 90°-70° 

= 20°

∴ y = 20°

∴ x – y = 28° -20° = 8 Proved.

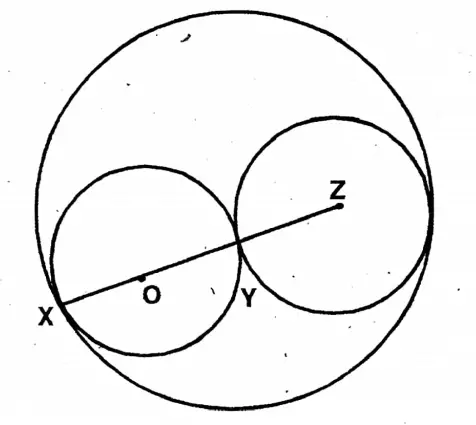
Question 7. Two circles with centres A and B touch each other internally. Another circle touches the larger circle externally at point x and the smaller circle externally at point y. If O is the centre of that circle, let us prove that AO+ BO is constant. 

Solution:

Given

Two circles with centres A and B touch each other internally. Another circle touches the larger circle externally at point x and the smaller circle externally at point y. If O is the centre of that circle

To prove AO+ BO = Constant

Join O, X, O, Y, O, A & Y, B

Two circles with centres A & B

The point of contact is on the line joining centres A &

centre B.

Again, the two circles with centre O & centre B, touch externally at Y.

Point Y is on the line joining YB.

Again, the two circles with centre O & A touch internally at X.

Point X is on the line joining OX.

Now, OA = AS – OX & OB = OY + YB

∴ AO+ BO = AX – OX + OY + YB 

= AX – OX + OX + YB.

AO + BO = AX + YB

= Constant Proved.

[as OX OY = radius of the circle with centre O & AX = Radius of the circle with centre A; YB = Radius of the circle with centre B.]

Question 8. Two circles have been drawn with centres A and B which touch each other externally at the point O. I draw a straight line passing through point O which intersects the two circles at P and Q respectively. Let us prove that AP || BQ. 

Solution:

Given

Two circles have been drawn with centres A and B which touch each other externally at the point O. I draw a straight line passing through point O which intersects the two circles at P and Q respectively.

To prove AP || BQ.

Join A, P & B, Q

In ΔAOP, AO = AP (Radius)

∴ ΔAOP is an issoceles triangle. 

∴ ∠APO = ∠AOP

In ΔBOQ, BO = BQ (Radius) 

∴ ΔBOQ is an issoceles triangle.

∴ ∠BOQ = ∠QOB

Now, the two circles with centres A & B touch externally at O,

AB is the line joining their centres.

∴ ∠AOP = ∠BOQ (vertically opposite)

:. ∠APO = ∠BQO

PQ cuts AP & BQ at P & Q, & produces two equal angles.

∴ They are alternate angles.

∴ AP || BQ Proved.

Question 9. Three equal circles touch one another externally. Let us prove that the centres of the three circles form an equilateral triangle.

Solution: Let the circles with centres A, B, and C touch externally at points P, Q and R. To prove ABC is an equilateral triangle.

Proof: Two circles with centres A & B touch each other at P.

∴ Point P is on the line, AB, joining the centre.

Similarly, point Q is on line BC & point R is on line CA.

As the radii of the three circles are equal, AP = PB = BQ = QC = CR + RA

∴ AP + PB = BQ + QC = CR + RA

i.e., AB = BC = CA

∴ ΔABC is an equilateral triangle.

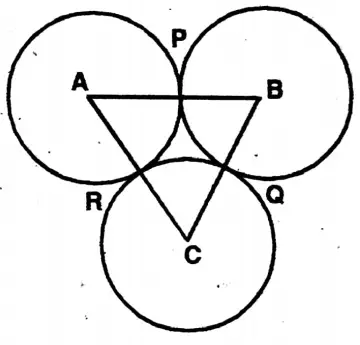
Question 10. Two tangents AB and AC drew from an external point A of a circle touch the circle at points B and C. A tangent drawn to point X lies on the minor arc BC intersects AB and AC at points D and E respectively. Let us prove which perimeter of AADE = 2AB.

Solution:

Given

Two tangents AB and AC drew from an external point A of a circle touch the circle at points B and C. A tangent drawn to point X lies on the minor arc BC intersects AB and AC at points D and E respectively.

To prove the perimeter of ΔADE = 2AB

Let O is the centre of the circle.

Join O,B, O,C, O,D & O,X In Quadrilateral OXDB

∠OBD = ∠OXD = 90°

∴ OXDB is a cyclic quadrilateral

whose OD is a diagonal?

Now in ΔOBD & ΔOXD,

1 OB = OX (Radii of the same circle)

2 OD common

& 3 ∠OBD = ∠OXD = 90°

∴ ΔOBD ≅ ΔOXD

∴ BD = DX

Similarly CE = XE

∴ (AD + DX) + (AE + EX) = (AD + BD) + (AE + CE)

AB+ AC = 2AB [∴ AB = AC]

Again, (AD + DX) + (AE + EX) AD+DE+ AE = Perimeter of ΔADE

∴ The perimeter of ΔADE = 2AB Proved.

 

Maths WBBSE Class 10 Solutions Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.2 Multiple Choice Question

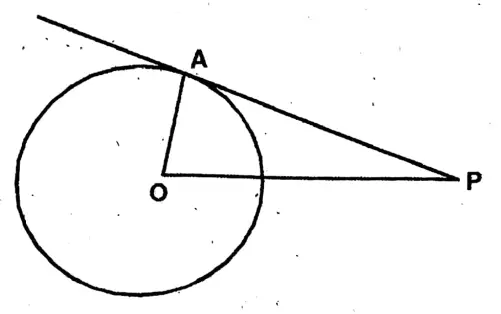
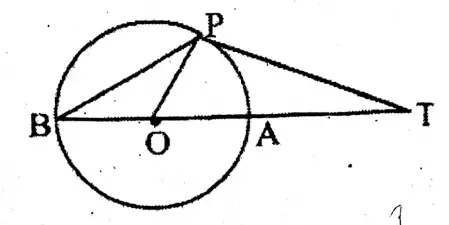
Question 1. A tangent drawn to a circle with centre O from an external point A touches the circle at point B. If OB = 5 cm, AO 13 cm, then the length of AB is

1. 12 cm.
2. 13 cm.
3. 6.5 cm.
4. 6 cm.

Solution:

Given

A tangent drawn to a circle with centre O from an external point A touches the circle at point B. If OB = 5 cm, AO 13 cm

AB2 = AO2 – OB2 = 132 – 52

= 169-25

= 144

.. AB = 12 cm.

Answer. 1. 12 cm.

Question 2. Two circles touch each other externally at point C. A direct common tangent AB touches the two circles at points A and B. The value of ZACB is

1. 60°
2. 45°
3. 30°
4. 90°

Answer. 4. 90°

Question 2. The length of the radius of a circle with centre O is 5 cm. P is a point at a distance of 13 cm from point O. The length of two tangents are PO and PR from point P. The area of quadrilateral PQOR is

1. 60 sq cm.
2. 30 sq cm.
3. 120 sq cm.
4. 150 sq cm.

Solution:

Given

The length of the radius of a circle with centre O is 5 cm. P is a point at a distance of 13 cm from point O. The length of two tangents are PO and PR from point P.

Area of quadrilateral

= APQR + APOQ

=(1/2 x5x12) + (1/2 x 5 x 12) sqm.

= 60 sq cm.

Answer. 1. 60 sq cm.

Question 4. The lengths of the radii of the two circles are 5 cm and 3 cm. The two circles touch each other externally. The distance between two centres of the two circles is

1. 2 cm.
2. 2.5 cm.
3. 1.5 cm.
4. 8 cm.

Solution:

Given

The lengths of the radii of the two circles are 5 cm and 3 cm. The two circles touch each other externally.

The distance between the centres

= Sum of their radii

= 5 cm + 3 cm = 8 cm

Answer. 4. 8 cm.

Question 5. The lengths of the radii of the two circles are 3.5 cm and 2 cm. The two circles touch each other internally. The distance between the centres of the two circles is

1. 5.5 cm.
2. 1 cm.
3. 1.5 cm.
4. None of these

Solution:

Given

The lengths of the radii of the two circles are 3.5 cm and 2 cm. The two circles touch each other internally.

The distance between the centres

= Difference between their radii

= (3.52) cm 

= 1.5 cm

Answer. 3. 1.5 cm.

Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.2 True Or False

1. P is a point inside a circle. Any tangent drawn on the circle does not pass through point P.

True

2. There are more than two tangents which can be drawn to a circle parallel to a fixed-line.

False

WBBSE Class 10 Maths Solutions Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.2 Fill In The Blanks

1. If a straight line intersects the circles at two points, then the straight line is called the Bisector of the circle.

2. If two circles do not intersect or touch each other, then the maximum number of common tangents that can be drawn is  4. (Four).

3. Two circles touch each other externally at point A. A common tangent drawn to the two circles at point A is a common Transverse tangent (direct/transverse)

Chapter 15 Theorems Related To Tangent Of A Circle Exercise 15.2 Short Answers

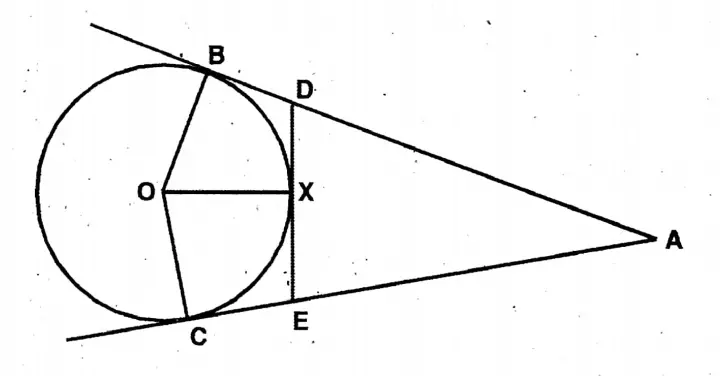
Question 1. In the adjoining figure, O is the centre and BOA is the diameter of the circle. A tangent drawn to a circle at point P intersects the extended BA at point T. If ∠PBO is 30°, let us find the value of ∠PTA.

Solution:

Given

In the adjoining figure, O is the centre and BOA is the diameter of the circle. A tangent drawn to a circle at point P intersects the extended BA at point T. If ∠PBO is 30°,

∠PBO = 30°

∴ ∠BPO = 30°.

∴ ∠BPT = 90° +30° = 120°

∴ In ΔBPT, ∠BPT = 120°

∠PBO = 30°

∠PTA 180° (120° + 30°) = 30°

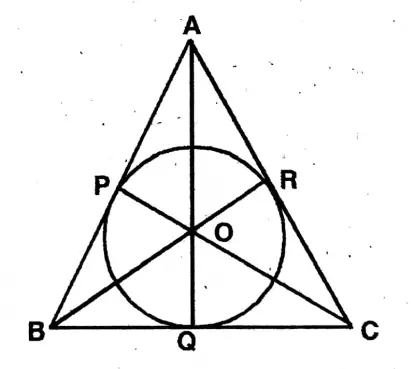
Question 2. In the adjoining figure, ABC circumscribed a circle and touches the circle at the points P, Q, R. If AP = 4 cm, BP = 6 cm, AC = 12 cm and BC = x cm, let us determine the value of x.

Solution.

Given

In the adjoining figure, ABC circumscribed a circle and touches the circle at the points P, Q, R. If AP = 4 cm, BP = 6 cm, AC = 12 cm and BC = x cm,

Join OP, OQ, OR & AO, BO, CO. 

AP = AR, BP = PQ, CQ = CR

∴ AR = 4 cm,

CQ = (10-4) cm

= 6 cm. 

BQ = 6 cm.

∴ x = BC = BQ + AC

= (6+6) cm 

= 12 cm.

Question 3. In the adjoining figure, three circles with centres A, B, and C touch one another externally. If AB = 5 cm, BC = 7 cm and CA = 6 cm, let us find the length of the radius of the circle with centre A.

Solution:

Given

In the adjoining figure, three circles with centres A, B, and C touch one another externally. If AB = 5 cm, BC = 7 cm and CA = 6 cm

AP = AB – BP

BP – BR =BC – CR

CR = CQ = AC – AQ

AP = AB – BC + CR

= AB- BC + AC – AQ

= AB+ AC (BC + AQ) 

= AB+ AC- (BC + AP)

AP + AP = AB+ AC – BC 

2AP=5+6-7=4

.: AP = 2 cm

∴ Length of the radius of the circle with centre A = 2 cm.

 

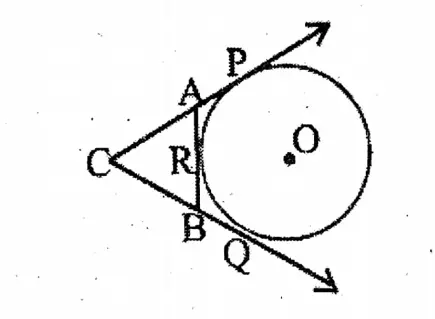
Question 4. In the adjoining figure, two tangents are drawn from external point C to a circle with centre O touch the circle at points P and Q respectively. A tangent drawn at another point R of a circle intersects CP and CA at points A and B respectively. If, CP is 11 cm. and BC= 7 cm, let us determine the length of BR.

Solution:

Given

In the adjoining figure, two tangents are drawn from external point C to a circle with centre O touch the circle at points P and Q respectively. A tangent drawn at another point R of a circle intersects CP and CA at points A and B respectively. If, CP is 11 cm. and BC= 7 cm

CP= CQ, CQ = 1 cm,

BQ = CQ- BC

= (11-7) cm = 4.cm.

Join R,Q

∴ From As BRD & ABQD

BR = BQ

∴ BR = 4 cm.

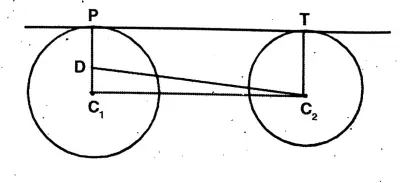
Question 5. The lengths of the radii of the two circles are 8 cm and 3 cm and the distance between their two centres is 13 cm. Let us find the length of a common tangent of two circles.

Solution: Let C₁ & C₂ are two centres of the two circles.

Radius of circle with center C₁ = 8 cm,

& Radius of circle with center C₂ = 3 cm.

PT is the common tangent

C₁PC₂T

Straight line from C_2,

parallel to PT cuts C₁P at D.

∴ PDC₂ T is a parallelogram.

DP = C₂T

& C₂D = PT.

C₁D = 8 – DP

= 8 – 3

= 5

∠DPT = 90°

∴ ∠C₁D₂ = 90°

\(\mathrm{DC}_2{ }^2=\mathrm{C}_1 \dot{\mathrm{C}}^2-\mathrm{C}_1 \mathrm{D}^2\)

= 13^2-5^2

= 12^2

∴ DC₂ = PT = 12 cm.