West Bengal Board Class 10 Math Book Solution In English
Chapter 16 Right Circular Cone Exercise 16.1
Question 1. But what is point B of the 2 of the right circular cone called?
Solution. Point B of the 2 is called the apex of the right circular cone. Again, the perpendicular AB on the circular base is called the Height of the right circular cone and BC is called the Slant height. The number of surfaces of a closed cone is 2. One is plane and the other is curved.
Question 2. I write the names of solid objects which are used in our house and whose shapes are like right circular cones.
Solution. Names of 4 solid objects (cone);
Conical hat;
Conical toy;
Funnel;
Top of a sharp pencil.
To make a right circular cone with one face open, лrl sq. unit paper is required, where r = Radius of cone and l= Slant height of the cone.
Read and Learn More WBBSE Solutions For Class 10 Maths
Application 1. Let us calculate the curved surface area of a right circular cone whose radius of the base is 1.5 m and slant height is 2 m.
Solution: Radius of the base of cone = r = 1.5 m.
Slant height (l) = 2 m.
Curved surface area = лrl = 22/7 x 1.5 x 2 sq m
= 9.43 sq m.
Application 2. If the area of the base of a cone is 78/7 sq. cm and the slant height is 13 cm, then let us calculate its curved surface area.
Solution: Let the length of the radius of the base of the cone be r cm.
According to the condition, 22/7 r2=78 4/7
∴r=5&h= 13 cm,
√132 +52 =√194 = 13.9 approx
∴ Curved surface area of the cone πrl sq. cm. = 218.23 sq. cm.
West Bengal Board Class 10 Math Book Solution In English
Application 3. If the circumference of the base of a cone is 660/7 cm and the slant height is 25 cm, then let us calculate the curved surface area of the cone.
Solution πrl= 2лrl/2 = 660/ 2×7 x 25
= 1178.57 sq cm.
Application 4. Let us write the total surface area of a cone whose length of the radius of the base is 1.5 cm and slant height is 2.5 cm.
Solution: The total surface area of the cone = 22/7 x 1.5(1.5+ 2.5) sq cm.
= 22/7 x 15/10 x 4 sq cm.
= 18.86 sq cm.
Application 5. Let us write the total surface area of a cone whose diameter of the base is 20 cm and slant height is 2.5 cm.
Solution: Radius of the base (r) = 20 cm/2
= 10 cm.
Slant height (l) 2.5 cm.
∴ Total surface area of the cone = πr(r + l)
= 22/7 x 10x (10+ 2.5) sq cm =
= 22/7 x 10 x 35 sq cm.
= 1100 sq cm.
Application 6. Let us calculate the slant height of a right circular cone whose circumference is 660/7 cm and height is 20 cm.
Solution: In the fig, Radius (OA) = r
& height (BO) = 20 cm.
∴ 2лr = 660/7
Or, 2 x 22/7 x r = 660/7
r =660/7 x 7/2×22
= 15 cm.
∴ AB²= OB² + OA²
= (20)² + (15)²
= 400+ 225
= 625
∴ AB = √625 = 25 cm.
∴ The slant height of cone = 25 cm.
West Bengal Board Class 10 Math Book Solution In English
Application 7. If the height of a conical flask of the science laboratory of the school is 4 dcm and the slant height is 6 dcm, then let us calculate the quantity of water that can be held in the flask.
Solution: Let the length of the radius of the base of the conical flask be r dcm.
∴ (5)²= r²+(4)²
or, r²= 5²-4² = 9
∴r = ±3
But the length of the radius can not be negative.
∴ r ≠ -3.
∴ r = 3
The quantity of water that can be held in that flask =1/3 x 22/7 x 3 x 3 x 4 = 37 cubic dcm.
Application 8. If the circumference of the base of the right circular cone is 2.2 m and the height is 45 dcm, then let us write by calculating its volume of it.
Solution: Circumference 2лr = 2.2m = 22 dcm
or, 2πr = 22
or, 2 x 22/7 x r = 22
∴r= 7/2
∴ Volume of the cone = 1/3 Tr2h
1/3 x 22/7 x 7/2 x7/2 x 45 cu dcm.
= 577.5 cu dcm.
West Bengal Board Class 10 Math Book Solution In English
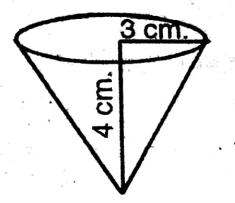
Application 9. The lengths of the two sides adjacent to the right angle of a right-angled triangle are 4 cm and 3 cm. Let us write by calculating the curved surface area, total surface area, and volume of the solid formed by completely revolving the triangle once by taking the longer side adjacent to the right angle as the axis.
[ Hints: The height of the right circular cone formed will be 4 cm and the radius will be 3 cm.]
Solution: Height of the cone (h) = 4cm
& Radius of the cone (c) = 3 cm.
∴ Slant height (l) = √4²+3²
= √16+9
= √25
= 5 cm.
1. Curved surface area = πrl
= 22/7 x 3 x 5 sq.cm
= 47.14 sq cm.
2. Total surface area = лr(r+ l)
= 22/7 x 3 (5+3) sq cm.
= 75.43 sq cm.
3. Volume of the cone = 1/3 πr²h
=1/3 x 22/7 x 3 x 3 x 4 cu cm.
= 37.71 cu cm.
Application 10. If the ratio of the heights of two right circular cones is 2:3 and the ratio of the lengths of their radii is 3:5, then let us write by calculating the ratio of the volumes of two cones.
Solution: Let the height of the 1st cone = 2x unit
& radius of 1st cone = 3y unit. & height of the 2nd cone = 3x unit
& radius of 2nd cone = 5y unit.
∴ Volume of 1st cone / Volume of 2nd cone = 1/3 π (3y)²2x / 1/3 π(5у)²3x
= 9y² . 2x / 25y² . 3x
= 18/75
= 6/25
∴ The ratio of volumes of two cones = 6: 25.
Class 10 WBBSE Math Solution In English
Application 11. The area of the base of a right circular conical tent is 13.86 sq.m. For making the tent, triple the cost of Rs. 5775 is required and if the price of 1 sq m. the tent is Rs. 250, then let us determine the height of the tent. Let us write by calculating, the air in the tent in liter.
Solution: Let the base radius of the tent be r m,
height be h m, and slant height be l m.
The area of the base is 13.86 sq. m.
According to the condition, 22/7 r² = 13.86
∴ r = 21 m.
The length of the radius is 2.1 m.
The quantity of triple in Rs. 5775 at the rate of Rs. 250 per meter = 5775/250 sq. m
= 23.1 sq.m.
∴ Curved (lateral) surface area = лrl sq.m = 23.1 sq.m
or, 22/7 x 21/10 x l = 23.1
∴ l= 7/2
∴ Slant height = 7/2 m = 3.5 m.
∴ h = + √l² – r² [height can not be negative]
= √(3.5)-(2.1)
= √(3.5+2.1)x(3.5-2.1)
= √5.6×1.4
= √7.84
∴ Height = 2.8 m
∴ The air occupied in the tent = 1/3 22/7 2.1 2.8
= 12.936 cum
= 12936 cu dcm
= 12936 liters.
Class 10 WBBSE Math Solution In English
Question 1. I have made a closed right circular cone whose radius of the base is 15 cm and slant height is 24 cm. Let us calculate the curved surface area and total surface area of that cone.
Solution: Radius of base of cone = (r) 15 cm
& slant height (l) 24 cm.
Curved surface area = πгl = 22/7 x 15 x 24 sq cm.
= 1131.43 sq cm.
= Total surface area = πr(r + l)
= 22/7 x 15 (15+24) sq cm.
= 22/7 x 15 x 39 sq cm. = 1838.57 sq cm.
Question 2. Let us determine the volume of the cone when
1. base area is 1.54 sq.m. and height is 2.4 m,
2. the length of a base diameter is 21m and the slant height is 17.5 m.
Solution: Let radius = r m & height (h) = 2.4 m.
Base area = πr2 = 1.54
or, 22/7 r2 = 1.54
∴ r2 = 1.54 x 7 / 22
= 0.49
∴ r= √0.49
= 7
1. Volume of the cone = 1/3 πr2h
= 1/3 x 22/7 x 7/10 x 7/10 x 24/10 cu m.
= 1.232 cu m.
2. Diameter = 21 m
∴ Radius = 21/2
= 10.5 m.
h²= l² – r²
=(17.5)²- (10.5)²
= 196
∴ h= √196
= 14 m.
Volume of the cone = 1/3 лr²h
= 1/.x 22/7 x 10.5 x 10.5 x 14 cu m.
= 1617 cu m.
WBBSE Solutions Guide Class 10
Question 3. Amina has drawn a right-angled triangle whose lengths of two sides adjacent to the right angle are 15 cm and 20 cm. Let us determine the curved surface area, total surface area, and volume of the solid which is formed by taking the side of length 15 cm which is formed by completely revolving the triangle once around the side of the triangle with the length of 15 cm, having been taken as an axis.
Solution: Height of the cone (h) = 15 cm.
& Radius (r) = 20 cm.
∴ Slant height (l) = √h² +r²
= √15²+20²
= √225+400
= 625
= 25 cm.
Curve surface area = лrl = 22/7 x 20 x 25 = 1571.73 sq cm.
Total surface area of cone = лr(г+ l) = 22/7 x 20 x (20+25) sq cm.
= 22/7 x 20 x 45 2828.57 sqcm.
Volume of the cone = 1/3 πr²h
= 1/3 x 22/7 x 20 x 20 x 15 cu cm.
= 6285.71 cu cm.
Question 4. If the height and slant height of a cone is 6 cm and 10 cm respectively, then let us determine the total surface area and volume of the cone.
Solution: Let the radius of the cone = r cm.
∴ r² = l²-h²
= (10)²- (6)²
= 100-36
= 64
∴ r = √64
= ± 8m.
As the radius cannot be negative
∴ radius (r) = 8 cm
∴ Total surface area of the cone = πг(г + l)
= 22/7 x 8 x (8+10)
= 22/7 x 8 x 18 sq cm.
= 452.57 sq cm.
Volume = 1/3 πr² = 1/3 x 8 x 8 x 6 cu cm.
= 402.28 cu cm.
WBBSE Solutions Guide Class 10
Question 5. If the volume of a right circular cone is 100 π cm3 and the height is 12 cm., then let us write by calculating the slant height of the cone.
Solution: Let the radius = r cm.
∴ 1/3 x 22/7x r2 x 12 = 100 x 22/7
4r² = 100
∴ r² = 25
r = √25
= 5
Slant height (l)=√h² + r²
= √12² +5²
= √144+25
= √169
= 13 cm.
Question 6.77 sq.m. triple is required to make a right circular conical tent. If the slant height of the tent is 7 m, then let us write by calculating the base area of the tent.
Solution: Let the radius = r cm.
According to problem
πrl = 77 or,22/7 x r x 7
= 77
∴ r = 7/2
∴ Area of the base = πr² = 22/7 x 7/2 x 7/2 sq cm.
= 38.5 sq cm.
Question 7. The base area of a right circular cone is 21 m and the height is 14 m. Let us calculate the expenditure to color the curved surface at the rate of Rs. 1.50 per sq.m.
Solution: Radius of a base of the cone (r) = 21/2 m.
& height (h)= 14 m.
∴ Slant height (0) = √h²+r²
=√(14)² + (21/2)²
=√1225/4
= 35/2m.
∴ Curved surface area of cone = πrl = 22/7 x 21/2 x 17.5 √
= 577.5 sq m.
Cost of coloring the curved surface area at the rate of Rs. 1.50/sq m.
= Rs. 577.5 x 1.5
= Rs. 866.25.
Ganit Prakash Class 10 Solutions Pdf In English
Question 8. The length of base diameter of a wooden toy of a conical shape is 10 cm. The expenditure for polishing the whole surfaces of the toy at the rate of Rs. 1.50 perm∴2 is Rs. 429. Let us calculate the height of the toy. Let us also determine the quantity of wood which is required to make the toy.
Solution: Radius of the base of the toy (cone) = 10/2
= 5 cm.
The curved surface area of = πrl
where l = slant height
According to the problem,
Trl Rs. 2.10 = Rs. 429
Or, 22/7 x 5 x l x2.10 = 429
l = 429 x 7/22 x 1/5 x 10/21
= 13. cm.
∴Height = √l² – r²
= √(13)² – (5)²
= 169-25
=√144
= 12 cm.
Volume of the toy = 1/3 лr2h= 1/3 x 22/7 x 5 x 5 x12 cum.
= 314.29 cum.
9. The quantity of iron sheet to make a boya of right circular conical shape is 75 3/7 m2. If the slant height of it is 5 m, then let us write, by calculating, the volume of air in the boya and its height. Let us determine the expenditure to color the whole surface of the boya at the rate of Rs. 2.80 per m2. [The width of the iron sheet is not to be considered while calculating.]
Solution: Let the radius = rm, slant height = 5 m.
Total surface area = лr(r+l) = 528/7
or, 22/7 x r x (5+r)= 528/7
or, r(r+5)= 528/7 x 7/25
or, r2 + 5r – 24 = 0
(r+8)(r-3) = 0
= r = -8 or,3.[But radius cannot be negative]
r=3
∴Height = √l²- r²
= √(5)²-(3)²
= √25-9
= √16
= 4.
Volume of air in the boya = 1/3лr2h = 1/3 x 22/7 x 3 x 3 x 4
= 37 5/7cum.
Cost to color the whole surface of the boy a = Rs. 2.80 x 528/7
= Rs. 211.2.
Ganit Prakash Class 10 Solutions Pdf In English
Question 10. In a right circular conical tent, 11 persons can stay. For each person 4m2 space in the base and 20 m3 air are necessary. Let us determine the height of the tent put up exactly for 11 persons.
Solution: Total space required to sit 11 persons in the conical tent = 11 x 4 = 44 sqm.
If the radius of the base of corner m,
& height of cone = h m.
∴πr² = 44
or, 22/7 r² = 44
∴ r² = 44×7 / 2
= 14 m.
:. The volume of the cone,
= 1/3 лr2 = 1/3 x 22/7 x 14 x h
According to the problem,
1/3 x 22/7x 14 x h
= 20 x 11
∴ h = 20 x 11 x3x 7/22 x 1/14
= 15m.
∴ Height of the tent = 15m.
Question 11. The external diameter of a conical coronet made off a thermocouple is 21 cm in length. To wrap up the outer surface of the coronet with foll, the expenditure will be Rs. 57.75 at the rate of 10 p per m2. Let us write by calculating, the height and slant height of the coronet.
Solution: Radius of a conical coronet = r = 21/2 cm.
Curved surface area = лrl where l = slant height
Cost to wrap up the outer surface of the coronet at the rate of 10 p per sq cm
= πrl x 10p.
According to the problem,
Trl x 10 = 577.5
22/7 x 21/2 x l x 10
= 5775 / 10
l = 5775x7x2 / 10x10x22x21
= 175/10
= 17.5 cm.
∴ Height = √(17.5)²-(10.5)²
=√(17.5+10.5)-(17.5-10.5)
= √28×7
= √2x2x7x7
= 14 cm.
Maths WBBSE Class 10 Solutions
Question 12. A heap of wheat is in the shape of a right circular cone, its base diameter is 9 m and its height is 3.5 m. Let us determine the total volume of wheat. Let us calculate the minimum quantity of plastic sheet to be required to cover up this heap of wheat. [suppose π= 3.14, √130 = 11.4]
Solution: Diameter of base = 9 cm…
Radius (r) = m;
height (h) = 3.5 m.
∴Total volume of wheat = 1/3πr2h = 1/3 x 3.14 x 9/2 x 9/2 x 3.5 cum.
=74.18 cum.
Slant height(l)=√h² +r²
= √(3.5)²+(4.5)²
= √81/4 + 49/4
= √130/4
= 11.4/2
= 5.7m
∴ Minimum quantity of plastic sheet required = πrl
= 3.14 x 4.5 x 5.7 sqm.
= 80.54 sqm.
Maths WBBSE Class 10 Solutions Chapter 16 Right Circular Cone Exercise 16.1 Multiple Choice Question
Question 1. If the slant height of a right circular cone is 15 cm and the length of the base diameter is 16 cm, then the lateral surface area of the cone is
1. 60л cm²
2. 68π cm²
3. 120л cm²
4. 130π cm²
Solution: rπ.8 × 15 = 120π
Answer. 3. 120 cm²
(II) If the ratio of the volumes of two right circular cones is 1:4 and the ratio of the radii of their bases is 4: 5, then the ratio of their heights is
1. 1:5
2. 5:4
3. 25: 16
4. 25: 64
Ans. 4. 25: 64
Question 2. Keeping the radius of a right circular cone the same, if its height of it is increased twice, its volume of it will be increased by
1. 100%
2. 200%
3. 300%
4. 400%
Answer. 1. 100%.
Question 4. If each of the radius and height of a cone is increased by twice its length, then its volume of it will be
1. 3 times
2. 4 times
3. 6 times
4. 8 times the previous one.
Answer. 4. 8 times the previous one.
Question 5. If the length of the radius of a cone is r/2 then the total surface area is unit and its slant height of it is 20 units,
1. 2лr (l+r) sq. unit
2. πr(l + r/4)sq. unit
3. πr (l+r) sq. unit
4. 2πrl sq. unit
Solution: Whole surface area = π.r/2(2l + r/2)
= πг(l + r/4) sq. unit
Answer. (b) πг(l + r/4) sq. unit
Chapter 16 Right Circular Cone Exercise 16.1 True Or False
1. If the length of the radius base of a right circular cone is decreased by half and its height is increased by twice of it, then the volume remains the same.
False
2. The height, radius, and slant height of a right circular cone are always the three sides of a right-angled triangle.
True
Maths WBBSE Class 10 Solutions Chapter 16 Right Circular Cone Exercise 16.1 Fill In The Blanks
1. AC is the hypotenuse of a right-angled triangle ABC, the radius of the right circular cone formed by revolving the triangle once around the side AB as the axis in BC
2. If the volume of a right circular cone is V cubic unit and the base area is A sq. unit, then its height is 3V/A
3. The lengths of the base radii and the heights of a right circular cylinder and a right circular cone are equal. The ratio of their volumes is 3: 1
Chapter 16 Right Circular Cone Exercise 16.1 Short Answers
Question 1. The height of a right circular cone is 12 cm and its volume is 100 cm3. Let us write the length of the radius of the cone.
Solution. The volume of the cone 1/3 πr²h = 100л
oг,1/3 πr² x 12 = 100л
∴ r² = 100/4
= 25
∴ r = +5
∴ The radius of the cone = 5 cm.
Question 2. The curved surface area of a right circular cone is √5 times its base area. Let us write the ratio of the height and the length of the radius of the cone.
Solution. Let the radius = r unit & height = h unit & slant height = l unit.
πrl = √5πr²
∴ l = √5r
∴ h² = l² – r²
= 5r²-r²
= 4r².
∴ h = 2r
.. Ratio of the height & the radius = 2/1
= 2:1
Question 3. If the volume of a right circular cone is V cubic unit, the base area is A sq. unit and the height is H unit, then let us write the value of AH/V
Solution. Let the radius = r unit & height = h unit.
∴ V = 1/3 πr²h;
А= r², H = h
AH/V = πr² xh / 1/3 πr²h
= 3
Maths WBBSE Class 10 Solutions
Question 4. The numerical values of the volume and the lateral surface area of a right circular cone are equal. If the height and the radius of the cone are H unit and r unit respectively, then let us write the value of 1/h² + 1/r²
Solution. The volume of the cone = 1/3 πr²h cu unit.
Surface area =πrl=sq unit. [l= slant height]
1/3 лr²h = лrl
1/3 rh = l
= 1/9 r²h² = l²
=h² + r² [as (2 = h² + r²]
or , 1/9 = h² / r²h² + r²/r²h²
or, 1/9 = 1/r² + 1/h²
∴1/h² + 1/r² = 1/9
Question 5. The ratio of the lengths of the base radii of a right circular cylinder and a right circular cone is 3: 4 and the ratio of their heights is 2: 3; let us write the ratio of the volumes of the cylinder and the cone.
Solution. Let the radius of the base of the cylinder = 3x unit &
radius of base of cone = 4x unit.
Again, the height of the cylinder = 2y unit &
height of the cone = 3y unit
Volume of cylinder / Volume of cone = л(3x)² x 2y / 1/3 л(4x)²x3y
= 9x² x 2y / 1/3 x 16x² x 3y
= 9/16
∴The ratio of the volume of cylinder and volume of cone = 9: 8.
