WBBSE Solutions For Class 10 Maths Chapter 17 Construction Of Tangent To A Circle Exercise 17.1
How many tangents can be drawn in a circle? Let us observe by drawing it. At a point in the circle, ![]()
[1/2] tangent/tangents can be drawn. But from the point outside the circle ![]() [1/2] tangent/tangents can be drawn on the circle.
[1/2] tangent/tangents can be drawn on the circle.
Answer. 1, 2.
Question1. Let us draw a circle with a radius of 3.2 cm length. Let us draw a tangent to the circle on any point of it.
Solution: In the PQ is a tangent at A to the circle with the centre O.
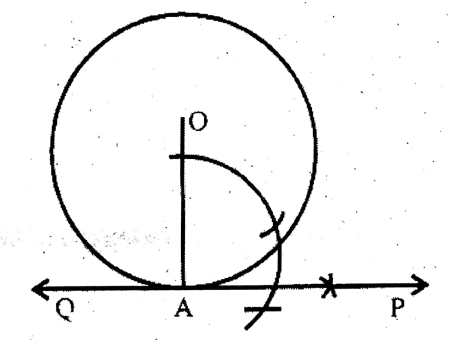
Read and Learn More WBBSE Solutions For Class 10 Maths
Question 2. By drawing a line-segment AB as a radius of 3 cm length. I draw a circle with centre A and a tangent to this circle at the point B.
Solution: In the PQ is the tangent at B to the circle with radius AB.
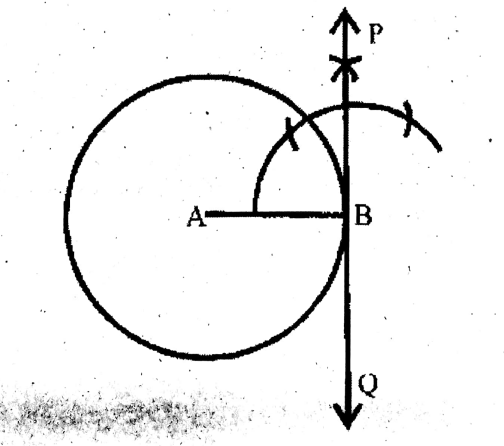
Question 3. I draw a circle with a radius of 2.5 cm in length. I take an external point at a distance of 6.5 cm from the centre. From this external point, I draw a tangent of the circle and measure the length of this tangent with a scale.
Solution:
In the AP is a tangent to the circle with centre O, from an external point A.
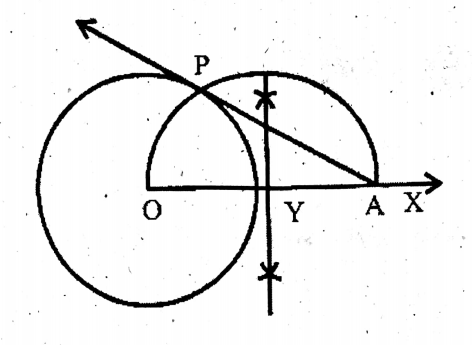
Question 4. I draw a circle with a radius of 2.8 cm in length. I take a point which is at a distance of 7.5 cm. from the centre. From that external point, I draw two tangents of the circle.
Solution: In the AP & AQ are two tangents from an external point A, of the circle with centre O.
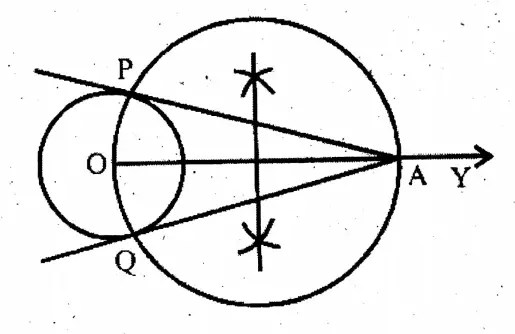
Question 5. PQ is a chord of a circle with centre O. I draw the tangents of the circle at the points P and Q.
Solution: In the AB & CD are two tangents at P & Q of the circle.
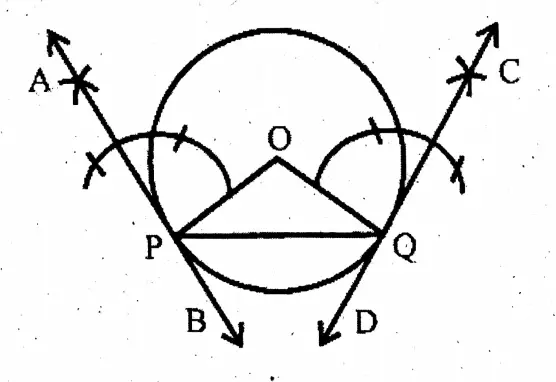
Question 6. I draw a line-segment XY of 8 cm in length and draw a circle by taking XY as a diameter. I draw the tangents of the circle at points X and Y and write the relation between these two tangents.
Solution: In PQ & RS are two tangents to the circle at X & Y & PQ || RS.
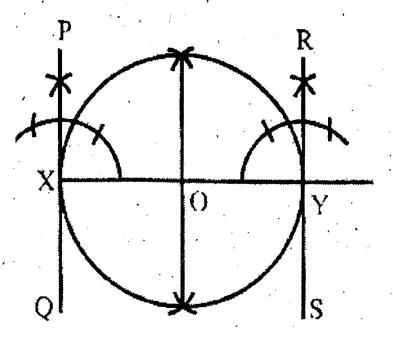
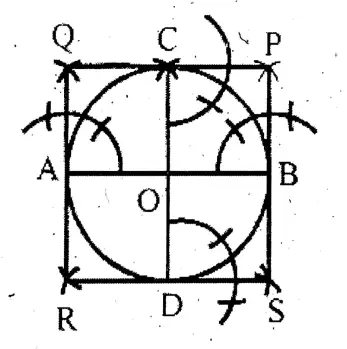
Question 7. By drawing any circle I draw two perpendicular diameters in it. I draw four tangents of the circle at four end points of two diameters and write the type of quadrilateral that is formed.
Solution: In the AB & CD are two diameters which are perpendicular to each other, & OR, RS, SP & PQ are 4 tangents at A, D, B, and C, and four end points of diameters. Quadrilateral, so formed is a square.
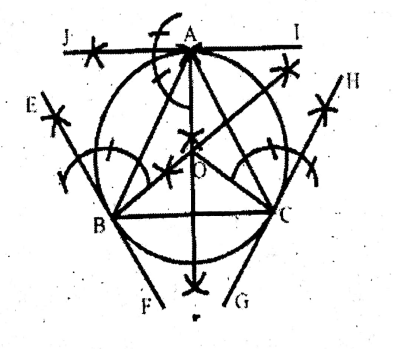
Question 8. By drawing an equilateral triangle ABC with sides of 5 cm in length, a circumcircle of it is drawn. Let us draw the tangents to that circumcircle at points A, B and C.
Solution: Circumcircle of ΔABC is drawn. Three tangents IT, EF, and GH are drawn at A, B & C points.
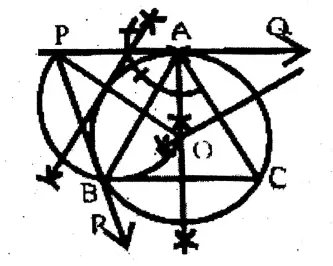
Question 9. I draw a circumcircle by drawing an equilateral triangle ABC with sides of 5 cm. length. I draw a tangent of the circle at point A and take point P on it such that AP is 5 cm. From point P, I draw another tangent of the circle and I write by observing the point at which this tangent has touched the circle.
Solution: ABC is an equilateral triangle, whose each side is 5 cm. PQ tangent is drawn at point A. Another tangent from P is drawn which touches the circle at B.
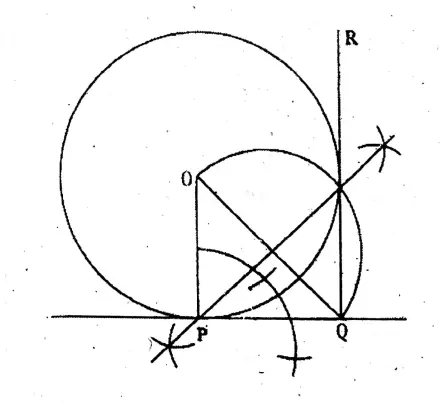
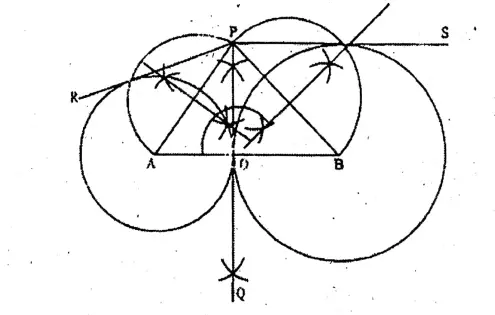
Question 10. O is a point on the line segment AB and I draw a perpendicular PQ on AB at the point O. I draw two circles with centres A and B and radii of AO and BO length respectively and write the name of PQ in respect to these two circles. I draw other two tangents of the two circles from the point P.
Solution:
O is a point on the line segment AB and I draw a perpendicular PQ on AB at the point O. I draw two circles with centres A and B and radii of AO and BO length respectively and write the name of PQ in respect to these two circles.
In the PQ is a transverse common tangent with respect to two circles. From the point P other two tangents, PR & PS are drawn.
Question 11. P is a point on a circle with centre O. I draw a tangent to the circle at point P and cut off a part ‘PQ’ equal in length to the radius of the circle from the tangent. I draw another tangent QR to the circle from point Q and write the value of∠PQR by measuring it with a protractor.
Solution:
P is a point on a circle with centre O. I draw a tangent to the circle at point P and cut off a part ‘PQ’ equal in length to the radius of the circle from the tangent.
In the other tangent QR is drawn from Q &∠PQR = 90°.