Maths WBBSE Class 10 Solutions Chapter 18 Similarity Exercise 18.1
Question 1. But will the two congruent figures be similar? Since the shape and size in the two congruent figures are equal, the two congruent are always 
[similar/not similar].
Answer. Similar.
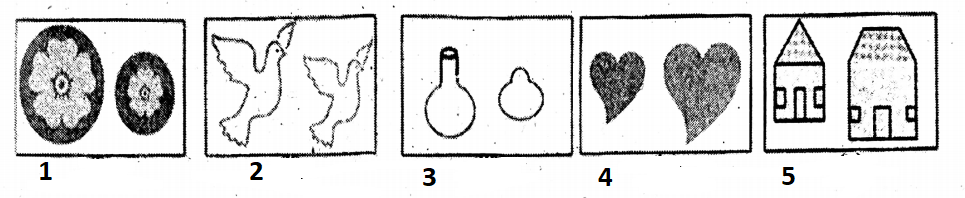
Question 2. I observe whether the pictures in each group are similar or not.
Answer. I am observing that the pictures of groups 1, 2, and 4 are similar to each other. But the pictures of the grups 3 and 5 are not similar to each other.
Read and Learn More WBBSE Solutions For Class 10 Maths
Question 3. Let us write the right answer in
1. All squares are [congruent/similar]
Answer. Similar.
2. All circles are [congruent/similar]
Answer. Similar.
3. All [equilateral/isosceles] triangles are always similar.
Answer. Equilateral.
“WBBSE Class 10 Maths Similarity Exercise 18.1 solutions”
Question 4. Two quadrilaterals will be similar if their corresponding angles are [equal/proportional] and corresponding sides are [unequal/proportional].
Answer. Equal and Proportional.
Chapter 18 Similarity Exercise 18.1 True or False
1. Any two congruent figures are similar.
Answer: True
2. Any two similar figures are always congruent.
Answer: False
3. The corresponding angles of any two polygonal figures are equal.
Answer: True
“West Bengal Board Class 10 Maths Chapter 18 Similarity Exercise 18.1 solutions”
4. The corresponding sides of any two polygonal figures are proportional.
Answer: True
5. The square and rhombus are always similar.
Answer: False
Question 5. Let us write examples of one pair of similar.
Solution:
Question 6. Let us draw a pair of figures which are not similar.
Solution:
The two 1 & 2 are similar and the two 3 & 4 are similar. Because their corresponding sides are and their corresponding angles are equal.
Answer. Similar.
Question 7. Now by cutting off ∠AA, and B, and putting them on ABC, I am observing that the two angles are overlapping.
Solution: I have got AA3 B3 = ABC, which are corresponding angles.
∴ A3 B3BC
Similarly by joining A1,B1, we shall get \(\frac{\mathrm{AA}_1}{\mathrm{~A}_1 \mathrm{~B}}=\frac{\mathrm{AB}_1}{\mathrm{~B}_2 \mathrm{C}}=\frac{1}{6}\) and A1,B1 || BC
By joining A2,B2, we shall get \(\frac{\mathrm{AA}_2}{\mathrm{~A}_2 \mathrm{~B}}=\frac{\mathrm{AB}_2}{\mathrm{~B}_2 \mathrm{C}}=\frac{2}{5}\) and A1,B2 || BC [Putting = /||]
What we shall get by joining A4 , B4 or A5 , B5 or A6 , B5 or A6 , B6
“WBBSE Class 10 Similarity Exercise 18.1 solutions explained”
Question 8. In a similar way, I have drawn another triangle and a straight line that has divided any two other sides (or their extended sides) in the same ratio and I am observing that the straight line is parallel to the third side.
Solution: I draw ΔABC, straight line DE, cut AB & AC at D & E proportionately,
AD/BD = AE/EC
∴ DE || BC
Again I draw AABC, straight line DE produced cuts in proportion.
AB/AD = AC/AE
∴ BC || DE
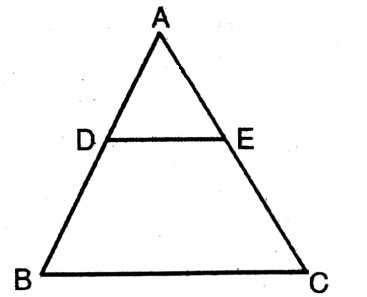
Application 1. In adjoining, DE || BC of ΔABC; if AD = 5 cm. DB = 6 cm and AE = 7.5 cm, then let us write by calculating the length of AC.
Solution:
Given
In adjoining, DE || BC of ΔABC; if AD = 5 cm. DB = 6 cm and AE = 7.5 cm,
In ΔABC, DE BC,
AD/DB = AE/EC [From Thales theorem]
5/6 = 7.5/EC
∴ EC = 7,5 + 6/5 cm
= 9 cm.
∴ AC = AE + EC
= 7.5cm + 9cm
= 16.5cm.
Length of AC = 16.5cm.
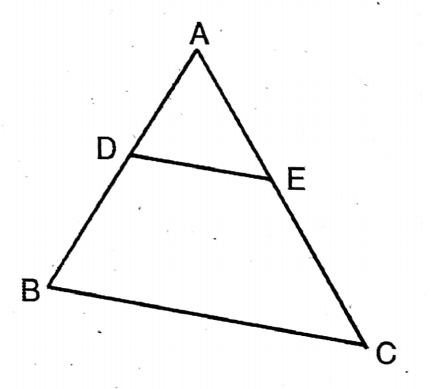
Application 2. If BC || DE in AABC, AD/DB = 2/5, and AC = 21 cm, then let us write by calculating the value of AE
Solution:
Given
If BC || DE in AABC, AD/DB = 2/5, and AC = 21 cm
As BC II BE
∴ AD/DB = AE/EC = 2/5
Set AE = x cm
∴ EC = (2x – x) cm
∴ X/21-x = 2/5
Or, 5x = 42 – 2x
or, 7x = 42
∴ x = 6
∴ AE = 6cm
The value of AE = 6cm
“WBBSE Class 10 Maths Exercise 18.1 Similarity problem solutions”
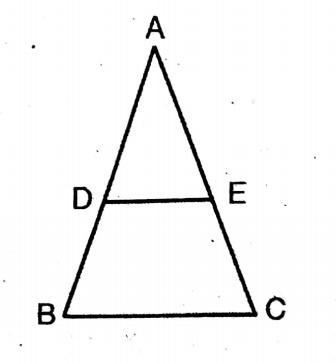
Application 7. With the help of the converse of Thales theorem, let us prove that the line segment joining two mid-points of a triangle is parallel to its third side.
Solution: In ΔABC,
D & E are the midpoints of AB & AC, respectively
Join D, E
∴ AD/BD = AE/EC = 1/1
∴ BC || DE
“Class 10 WBBSE Maths Exercise 18.1 Similarity step-by-step solutions”
∴ The line segment joining two midpoints of a triangle is parallel to its third side.
