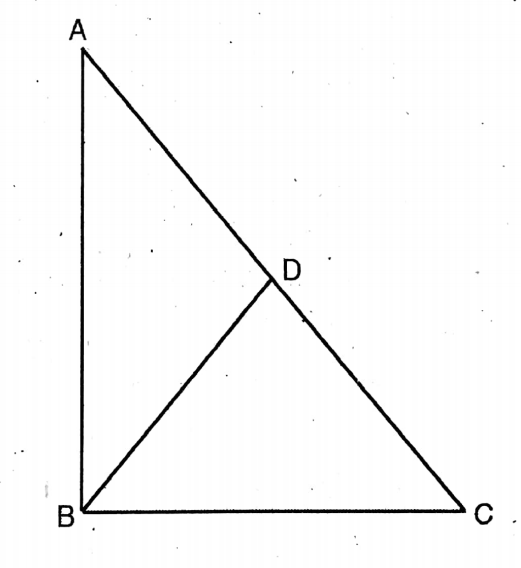
West Bengal Board Class 10 Math Book Solution In English Chapter 18 Similarity Exercise 18.3
Question 1. Which pairs of the following triangles are similar let us write by calculating it.
Solution: ΔABC & ΔPQR are equiangular.
AB/QR = BC/PQ = AC/PR = 1/2
Read and Learn More WBBSE Solutions For Class 10 Maths
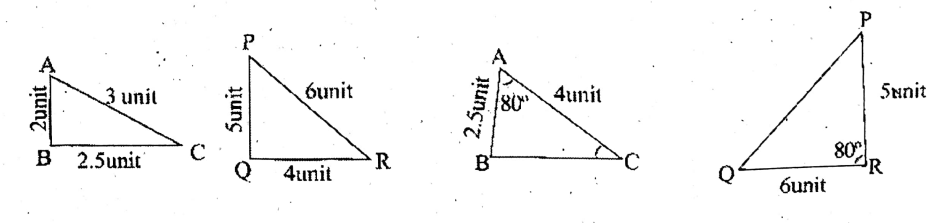
Question 2. I look at the following pair of triangles and I write by calculating the value of ∠A.
Solution: ∠A 180° (75° + 65°)
= 180°-140°
= 40°
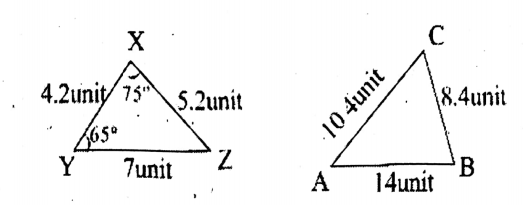
Question 3. In our field, a shadow of 4 cm length of a stick with a length of 6 cm has fallen on the ground. At the same time, if the length of the shadow of a high tower is 28 m, then let us write by calculating the height of the tower.
Hints:
Given
In our field, a shadow of 4 cm length of a stick with a length of 6 cm has fallen on the ground. At the same time, if the length of the shadow of a high tower is 28 m,
Let PQ be the tower and AB be the stick.
∴ BC= 4 cm, QC = 28 cm.
ΔPQC and ΔABC are similar.
PQ/AB = QC/BC
Solution: Let PQ be a tower & AB is a stick.
AB = 6 cm BC= 4 cm & QC = 28 m.
ΔPQC & ΔABC are equiangular.
∴ They are similar.
PQ/AB = QC/BC
PQ/6 = 28/4
4 PQ = 28 x 6
∴ PQ = 28×6 / 4
= 42
∴ Height of the lower = 42 m.
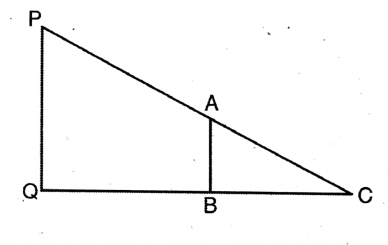
Question 4. Let us prove that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is equal to half of it.
Solution: Let D & E be the midpoints of sides AB & AC of ΔABC.
Join D, E.
To prove DE || BC & DE = 1/2 BC.
Proof: As D is the midpoint of AB,
∴ AD = DB or, AD/DB = 1 ——(1)
Again, as E is the midpoint of AC,
∴ AE = EC or, AE/EC = 1 ——–(2)
From (i) & (ii),
AD/DB = AE/EC
∴ DE || BC.
Again, in triangles ADE & ABC, we get ∠DAE = ∠BAC & ∠ADE = ∠ABC.
∴ ΔADE & ΔABC are equiangular.
AD/AB = AE/EC = DE/BC
But AD/AB = 1/2 [as D is the midpoint of AB]
DE/BC = 1/2
or, DE = 1/2 BC Proved.
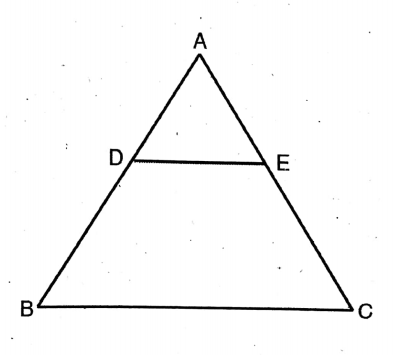

Question 5. Two parallel lines intersect three concurrent straight lines at points A, B, C, and X, Y, and Z respectively. Let us prove that AB: BC = XY: YZ.
Solution:
Given
Two parallel lines intersect three concurrent straight lines at points A, B, C, and X, Y, and Z respectively.
Let OX, OY & OZ straight lines pass through O; two parallel straight lines ABC & XYZ cut them at A, B, C & X, Y, Z.
To prove, AB : BC = XY: YZ
Proof: In ΔOXY, AB || XY.
∴ ∠OXY = ∠OAB & ∠OYX = ZOBA
Now in ΔOXY & ΔOAB,
∠OXY = ∠OAB
& ∠OYX = ∠OBA
ΔOXY & ΔOAB are equiangular.
OA/OX = OB/OY = AB/XY
Similarly from, ΔOYZ & ΔOBC,
OB/OY = OC/OZ = BC/YZ
AB/XY = OB/OY = BC/YZ
AB/XY = BC/XY
or, AB/YZ = BC/YZ
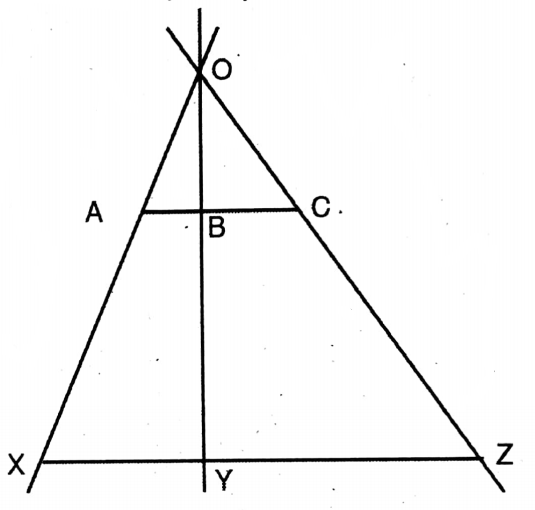
Question 6. I have drawn a trapezium PQRS whose PQ || SR; if two diagonals PR and QS intersect each other at the point O, then let me prove that OP: OR = OQ: OS; if SR = 2PQ, then let me prove that the point O will be a tri-sector of each of the two diagonals.
Solution:
Given
I have drawn a trapezium PQRS whose PQ || SR; if two diagonals PR and QS intersect each other at the point O, then let me prove that OP: OR = OQ: OS; if SR = 2PQ,
In trapezium PQRS, PQ || SR
& QS is the transversal
∴ ∠PQS = ∠QSR (alternate)
i.e., ∠PQO = ∠OSR
Again, PQ || SR & PR is a transversal.
∴ ∠QPR = ∠PRS (alternate)
i.e., ∠QPO = ∠ORS
& ∠POQ = ∠SOR (vertically opposite)
Now in As ∠POQ & ∠SOR
∠PQO = ∠OSR; ∠QPO = ∠ORS & ∠POQ = ∠SOR
∴ ΔPOQ & ΔSOR are equiangular.
OP/OR = OQ/OS = PQ/SR
OP/OR = OQ/OS Proved.
Now, if SP = 2PQ
∴ OP/OR = PQ= 2PQ 1/2
or, OQ = 2. OP.
OR: OP = 2:1
OQ/OS = PQ = 2PQ = 1/2 or, OQ = 20S
∴ OQ: OS = 2:1
Question 7. PQRS is a parallelogram. If a line passing through the point S intersects PQ and extended RQ at the points X and Y respectively, then let us prove that PS: PX = QY: QX = RY: RS.
Solution:
Given
PQRS is a parallelogram. If a line passing through the point S intersects PQ and extended RQ at the points X and Y respectively
In parallelogram PQ || SR & SX is a transversal.
∴ ∠XSR = 2PXS (alternate angles)
Again, SP || YR & SY is transversal P.
∴ ∠PSX = XYO (alternate angles) PS || YR & PQ is transversal.
∠SPX = YOX (alternate)
& ∠PXS = ∠QXY (vertically opposite)
Now, in triangles PXS & ∠OXY, ∠PSX = ∠XYQ; ∠SPQ = ∠YQX
& ∠PXS = ∠YXQ
∴ The triangles are equiangular.
PX/XQ = SX/XY = PS/QY
PX/XQ = PS/QY
or, PS/PX = QY/QX——–(1)
Again, PQ || SR & SY is transversal.
∴ ∠YSR = ∠YXQ (Similar angle)
Now, PQ || SR & YR is a transversal
∴ ∠YRS = ∠YQS (Similar)
Now, in ΔSYR & ΔXYQ
∠YSR = ∠ΥΧQ
∠YRS = ∠YQS & ∠SYR = ∠XYQ
∴ ΔSYR & ΔXYQ are equiangular.
SY/XY = YR/YQ = SR/QX
YR/YQ = SR/QS——-(2)
From (i) &. (ii),
PS/PX = QY/QS = RY/PS
∴ PS: PXQY: QX = RY: RS Proved.
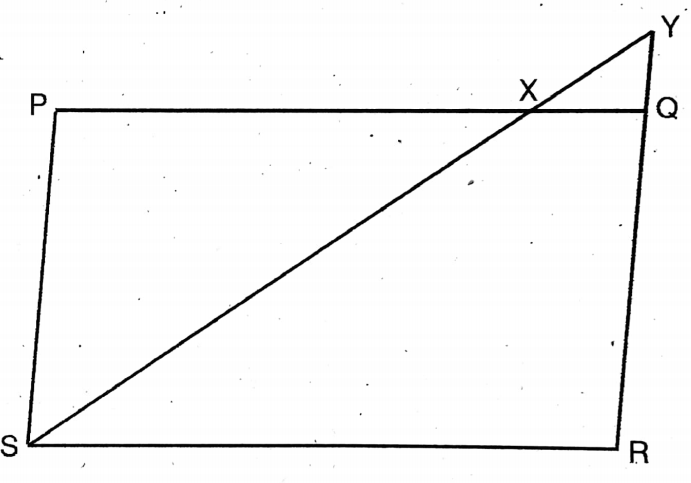
Question 8. The two acute-angled triangles AABC and APQR are similar. Their circumstances are X and Y respectively; if BC and QR are corresponding sides, then let us prove that BX: QY BC: QR.
Solution:
Given
The two acute-angled triangles AABC and APQR are similar. Their circumstances are X and Y respectively; if BC and QR are corresponding sides
As ABC & PQR are equiangular.
∴ ABC = PQR & ACB = PRQ
Now, in ΔABC
ABX = XBC [as BX is the bisector of ABC]
ACX = XCB [as CX is the bisector of ACB]
Now in ΔPQR,
PQY=YRQ [as QY is the bisector of PQR]
& PRY = YRQ [as YR is the bisector of PRQ]
∴ XBC= YQR & XCB = YRQ
∴ BXC & QYR are equiangular.
BX/QY = XC/YR= BC/QR
BX/QY = BC/QR
∴ BX: QY = BC: QR Proved.
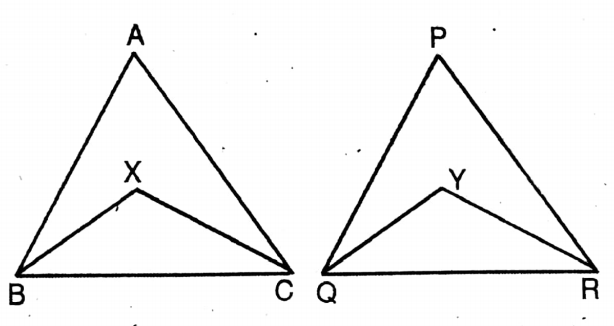
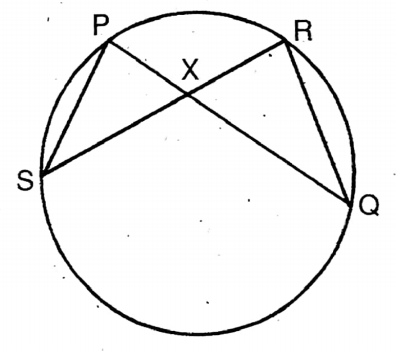
Question 9. The two chords PQ and RS of a circle intersect each other at point X within the circle. By joining P, S, and R, Q, let us prove that APXS and ARSQ are similar. From this, let us prove that PX: XQ = RX: XS. or, If two chords of a circle intersect internally, then the rectangle of two parts of one is equal to the rectangle of two parts of the other.
Solution:
Given
The two chords PQ and RS of a circle intersect each other at point X within the circle. By joining P, S, and R, Q,
Join S, P & Q, R.
Proof: ∠SPQ &∠SRQ are the angles at the circumference on the same segment SQ.
∴ ∠SPQ ∠SRQ
or, ∠SPX = ∠XRQ
Again, ∠PSR & ∠PQR are the angles at the circumference on the same segment PR.
∴ ∠PSR = ∠PQR
Or, ∠PSX = ∠XQR
∴ ΔPSX & ΔROX are equiangular. Proved.
PX/RX = XS/XQ
or, PX. XQ = RX. XS Proved.
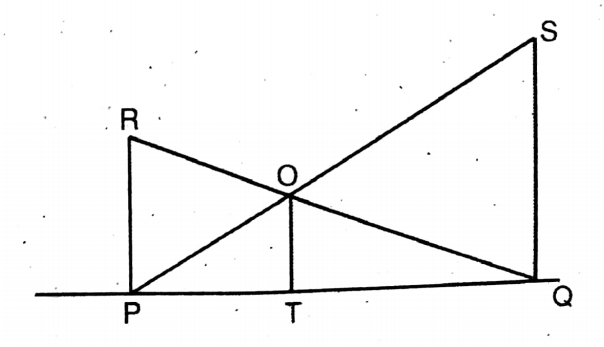
Question 10. The two points P and Q are in a straight line. At the points, P and Q, PR, and QS are perpendicular on the straight line. PS and QR intersect each other at the point O.OT is perpendicular to PQ. Let us prove that 1/OT = 1/PR = 1/QS
Solution:
Given
The two points P and Q are in a straight line. At the points, P and Q, PR, and QS are perpendicular on the straight line. PS and QR intersect each other at the point O.OT is perpendicular to PQ.
In ΔPQR, OR || RP [as OT ⊥ PQ & RP ⊥ PQ]
OT/PR = TQ/PQ
∴ PQ = TQ.PR/OT——–(1)
Again, in ΔPQS, OT || QS.
OT/QS = PT/PQ
∴ PQ = PT.QS/OT ——(2)
From (1) & (2), TQ. PR= PT. QS
or, TQ. PR = (PQ – TQ). QS
or, TQ. PR = PQ. QS – TQ. QS
or, TQ(PR+ QS) = PQ. QS
or, TQ(PR+QS) = TQPR.QS /OT
or, PR+QS/PR.QS = 1/OT
or, PR/PRQS + QS/PRQS = 1/OT
or, 1/PR + 1/QS = 1/OT Proved.
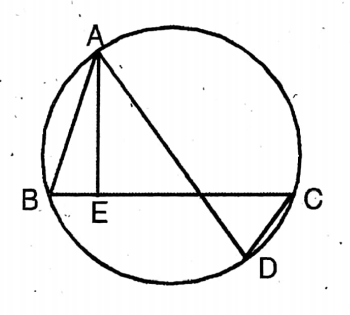
Question 11. ABC is inscribed in a circle; AD is the diameter of the circle and AE is perpendicular to side BC, which intersects side BC at point E. Let us prove that AAEB and AACD are similar. From this, let us prove that AB.AC = AE.AD.
Solution:
Given
ABC is inscribed in a circle; AD is the diameter of the circle and AE is perpendicular to side BC, which intersects side BC at point E.
From ΔABE & ΔACD, we get ∠AEB = ∠ACD = 90° as AD is a diameter.
∴ ΔBF = ΔDC (Both are on the same segment AC)
∴ <BAE=<DAC
∴ ΔABE & ΔACD are equiangular.
AB/AD = AE/AC
or, AB :AC = AD :AE Proved.
Application 1. In ΔABC, ∠ABC = 90° and BDL AC; if AB = 6 cm and BD = 3 cm, and CD = 5.4 cm, then let us write by calculating the length of BC.
Solution:
Given In ΔABC, ∠ABC = 90° and BDL AC; if AB = 6 cm and BD = 3 cm, and CD = 5.4 cm
Find BC.
∴ B 90°
∴ CBD + DBA = 90°——–(1)
Again, in DBA, D = 90° ..DBA + BAD = 90°
From (1) & (2), BAD = CBD
Again, DCB + CBD = DBA + BAD (= 90°)
or, DCB= DBA
∴ In ABD & CBD,
BAD = CBD; DCB = DBA; BDA = 90° = CDB
As ABD & CBD are equiangular.
AD/BD = BD/CD = AB/BC
AD = BDxBD/DC= 3 X 3 X 10 / 54
= 5/3
∴ BC= AB X BD / AD
= 6 X 3/ 5/3
= 54/ 5/3
= 10 4/5
∴ BC = 10 4/5 cm.
length of BC = 10 4/5 cm.