Maths WBBSE Class 10 Solutions Chapter 18 Similarity Exercise 18.4
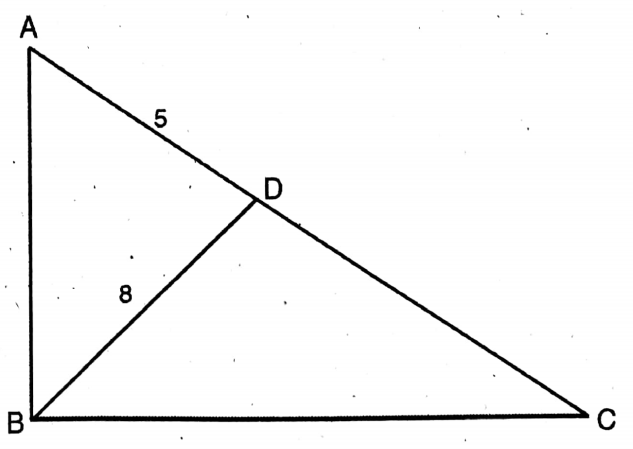
Question 1. In AABC, ZABC = 90° and BD L AC; if BD = 8 cm and AD = 5 cm, then let us calculate the length of CD.
Solution:
Given
In AABC, ZABC = 90° and BD L AC; if BD = 8 cm and AD = 5 cm
In ΔADB, (AB)²= (BD)² + (AD)²
or, (AB)² = (8)² + (5)²= 64+ 25 = 89
∴ AB = √89
From ΔABC, (AB)² + (BC)² = (AC)²
or, AB²+ BC² = (AD + CD)²
AB² + BC² = AD²+2.AD.CD + CD²——–(1)
Again, from ABDC, BC² = CD²+ BD² —— (2)
Read and Learn More WBBSE Solutions For Class 10 Maths
From (1) & (2),
AB²+ BC² – BC² = AD²+ 2AD.CD + CD² – CD²-BD²
or, AB² = AD²+2AD.CD – BD²
or, 89 = 25+ 10.CD-64
or, 10CD = 89 + 64-25 = 153-25 =
∴ CD = 12.8/10
= 12.8cm.
The length of CD = 12.8cm.
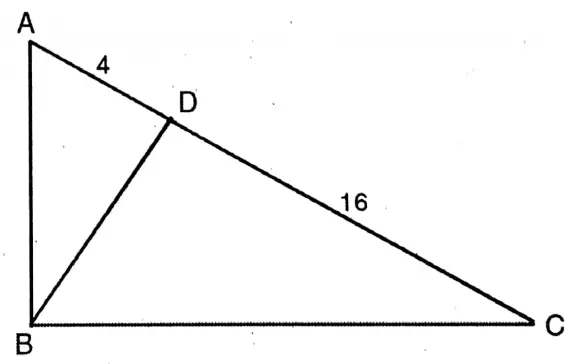
Question 2. AABC is a right-angled triangle whose B is right and BDL AC; if AD = 4 cm and CD = 16 cm, then let us calculate the lengths of BD and AB.
Solution:
Given
AABC is a right-angled triangle whose B is right and BDL AC; if AD = 4 cm and CD = 16 cm
From ΔABC, AB² = BD²+ AD²————– (1)
& from ΔBDC, BC² = BD²+ CD².
Adding, AB²+ BC² = 2BD²+ AD² + CD²——-(2)
or, AC² = 2BD² + 16 + 256
or, (20)²= 2BD²
= 400-272 128
∴ BD² = 64 .. BD = 8.
From (1), AB² = BD² + AD²
or, AB² 64+16= 80
∴ AB = √80 cm
= 4√5 cm.
The lengths of BD and AB = 4√5 cm.
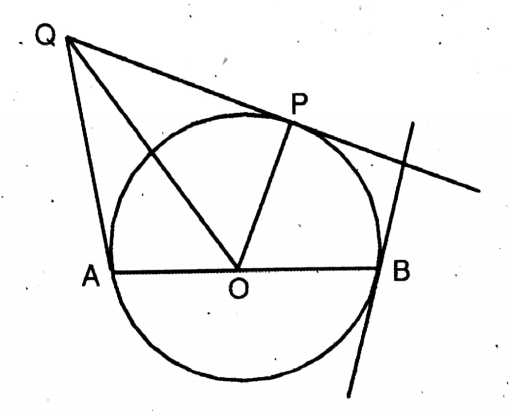
Question 3. AB is the diameter of a circle with center O. P is any point on the circle, the tangent drawn through point P intersects the two tangents drawn through points A and B, at points Q and R. respectively. If the radius of the circle is r, then let us prove that, PQ.PR = r2.
Solution:
Given
AB is the diameter of a circle with center O. P is any point on the circle, the tangent drawn through point P intersects the two tangents drawn through points A and B, at points Q and R. respectively.
Join OP, OQ, OR.
AQ & PQ are two tangents at A & P of the
circle with center O.
∴ ∠AOQ = ∠POQ
Similarly, as PR & BR are two tangents,
∴ ∠PQR = ∠BOR
∴ ∠AOQ + ∠BOR = ∠POQ + <POR
Again, (∠AOQ+ ∠BOR) + (∠POQ + <POR) = 180°
or, 2(∠POQ + ∠POR) = 180°
∴ ∠POQ + ∠POR = 90°
∴ ∠QOR = 90°
∴ ΔQOR is a right-angled triangle.
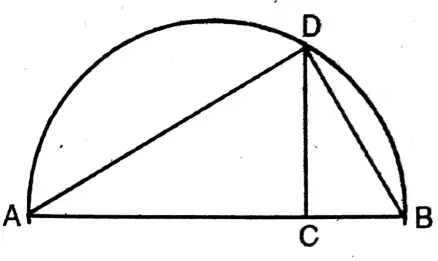
Question 4. I have drawn a semicircle with a diameter AB. I have drawn a perpendicular on AB from any point ‘C’ on AB which intersects the semicircle at point D. Let us prove that CD is the mean proportional of AC and BC.
Solution:
Given
I have drawn a semicircle with a diameter AB. I have drawn a perpendicular on AB from any point ‘C’ on AB which intersects the semicircle at point D.
With AB diameter a semicircle is drawn.
CD perpendicular is drawn on AB
which cuts the circumference at D.
To prove, CD is the mean proportional of AC & BC.
Join A, D, B, D
Proof, ∠ADB = 90°
Again, the CD is perpendicular to AB from D.
∴ ΔADC & ADBC are equiangular.
AC/DC = AC/DC = DC/CB
AC/DC = DC/CB
or, CD² = AC. CB
.. CD is the mean proportional of AC & BC.
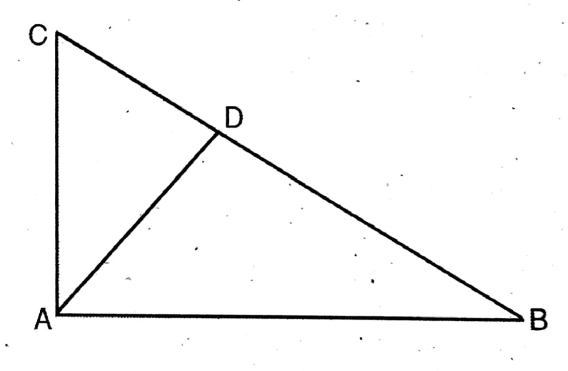
Question 5. In the right-angled triangle ABC, A is a right angle. AD is perpendicular on the hypotenuse BC; let us prove that ΔABC/ΔACD = BC²/AC².
Solution:
Given
In the right-angled triangle ABC, A is a right angle. AD is perpendicular on the hypotenuse BC;
In right-angled AABC, A = 90°,
& AD is perpendicular on hypotenuse BC.
To prove ΔACD/ΔABC = BC∠/AC∠
Proof: ACD & ABC are equiangular.
AC/BC = AD/AB
or, AC/BC = CD/AC
∴ AC² = BC. CD
Now, AABC/AACD = ½ BC X AD / ½ CD X AD =BC/DC
= BC²/BC.CD = BC²/AC²
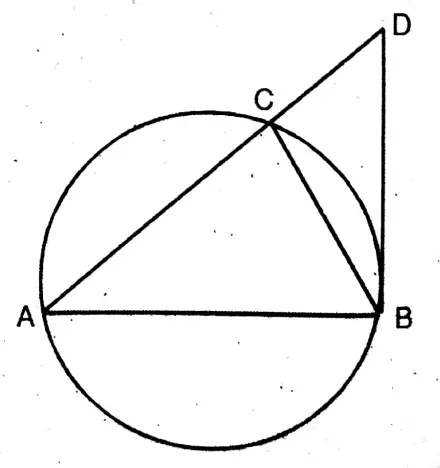
Question 6. AB is a diameter of a circle with center O. A line drawn through point A intersects the circle at point C and the tangent through B at point D. Let us prove that:
(i) BD2 = AD. DC;
(ii) The area of the rectangle formed by AC and AD for any straight line is always equal.
Solution:
Given
AB is a diameter of a circle with center O. A line drawn through point A intersects the circle at point C and the tangent through B at point D.
(1) Join B, C.
∴ ∠ACB is a semi-circle angle.
∴ ∠ACB = 90°
∴ ΔACB is a right-angle triangle.
Again, BD is a tangent at B on the diameter AB.
∴ AB ⊥ BD
∴ ΔABC is a right-angle triangle.
∴ ΔABD & ΔACD are similar.
BD/AD = CD/BD
∴ BD² = AD.CD Proved.
Solution: (2) Area of the rectangle formed by AD & AC = AD X AC
= Area of the square = AB² as AB is the mean proportional of AC & AD
∴ AB² = AC.AD.
Ganit Prakash Class 10 Solutions Pdf In English Chapter 18 Similarity Exercise 18.4 Multiple Choice Question
Question 1. In AABC and ADEF, if AB/DE = BC/FD = AC/EF then
1. ∠B = ∠E
2. ∠A = ∠D
3. <B = <D
4. ∠A = ∠F
Solution: B = <D
Answer. 3. <B = <D
Question 2. In ΔDEF and ΔPQR, if D = Q and R = ∠E, then let us write which of the following is not right:
1. EF/PR = DF/PQ
2. QR/PQ = EF/DF
3. DE/QR = DF/PQ
4. EF/RP = DE/QR
Answer. 2. QR/PQ = EF/DF
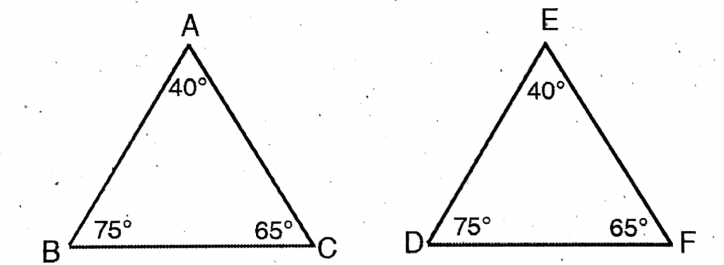
Question 3. In AABC and ADEF, if ZA = ZE = 40°, AB : ED = AC: EF and F = 65°, then the value of B is
1. 35°
2. 65°
3. 75°
4. 85°
Solution:
Given
In AABC and ADEF, if ZA = ZE = 40°, AB : ED = AC: EF and F = 65°,
Here ∠A = ∠E = 40
AB:ED = AC:EF
& F = 65°
∴ ∠∠C = 65 & ∠B = 180° (40° + 65°) = 75°
Answer. 3. 75°
Question 4. In AABC and APQR, if AB/QR = BC/PR = CA/PQ then
1. ∠A = ∠Q
2. ∠A = ∠P
3. ∠A = ∠R
4. ∠B = ∠Q
Solution :
Here as AB/QR = BC/RP = CA/PQ
∴ ∠A = ∠Q
Answer. 1. ∠A=∠Q
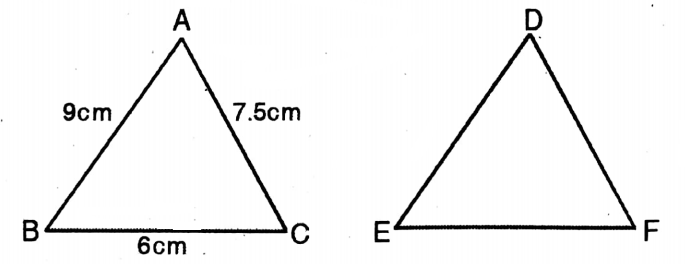
Question 5. In AABC, AB = 9 cm, BC = 6 cm, and CA = 7.5 cm. In ADEF the corresponding side of BC is EF; EF = 8 cm and if ΔDEF~ ΔABC, then the perimeter of ADEF will be
1. 22.5 cm.
2. 25 cm.
3. 27 cm.
4. 30 cm.
Solution :
Given
In AABC, AB = 9 cm, BC = 6 cm, and CA = 7.5 cm. In ADEF the corresponding side of BC is EF; EF = 8 cm and if ΔDEF~ ΔABC
Perimeter of ABC = (9+6 +7.5) cm
= 22.5 cm
Let the Perimeter of DEF = x cm.
As ABC & DEF are similar
The perimeter of ΔABC/BC = Perimeter of ΔDEF/EF
22.5 cm/6 cm = x cm/8 cm
or, 22.5 /6 = X/8
or, 6x 8 x 22.5
x = 8×22.5
= 4 × 7.5
= 30 cm.
Answer. 4. 30 cm.
WBBSE Solutions Guide Class 10 Chapter 18 Similarity Exercise 18.4 True Or False
1. If the corresponding angles of two quadrilaterals are equal, then they are similar.
Answer: False
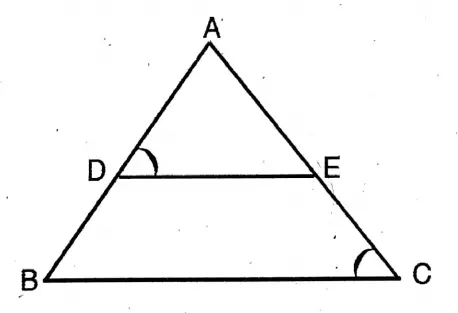
2. In the adjoining figure, if ∠ADE = ∠ACB then ΔADE-ΔACB.
Answer: True
3. In ΔPQR, D is a point on the side QR so that PDI QR; so ΔPQD = ΔRPD.
Answer: False
Class 10 WBBSE Math Solution In English Chapter 18 Similarity Exercise 18.4 Fill In The Blanks
1. Two triangles are similar if their Similar sides are proportional.
2. The perimeters of ABC and DEF are 30 cm and 18 cm respectively. ABC ~ DEF; BC and EF are corresponding sides. If BC= 9 cm, then EF = 5.4 cm.
Solution: Perimeter of ADEF/Perimeter of ΔABC = Length of EF/Length of BC
or, 30 cm/18cm = 9 cm/Length of EF
.. Length of EF = 18×9 / 30
= 5.4 cm.
Class 10 WBBSE Math Solution In English Chapter 18 Similarity Exercise 18.4 Short Answers
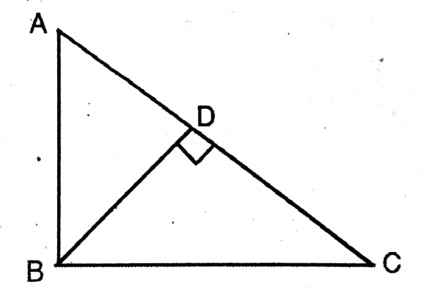
Question 1. In the adjoining figure, if ∠ACB = ∠BAD, ∠AC = 8 cm, ∠AB = 16 cm, and A∠D = 3 cm, then let us write the length of BD.
Solution.
Given
In the adjoining figure, if ∠ACB = ∠BAD, ∠AC = 8 cm, ∠AB = 16 cm, and A∠D = 3 cm
As ΔABD ~ ΔADC
or, AB/AC = BD/AD
.. BD = 16×3 / 8
6 cm.
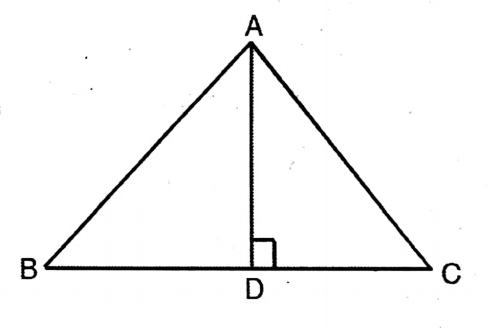
Question 2. In the adjoining figure, ∠ABC = 90° and BDL AC; if AB = 5.7 cm, BD = 3.8 cm, and CD = 5.4 cm, then let us determine the length of BC.
Solution.
Given
In the adjoining figure, ∠ABC = 90° and BDL AC; if AB = 5.7 cm, BD = 3.8 cm, and CD = 5.4 cm,
Here ΔABD ~ ΔBDC
.. BD² = AD x CD
or, (3.8)² = AD x 5.4
∴ AD = 3.8×3.8 / 54 x 10
= 19×19 / 27 x 5 cm.
BC/AB = CD/BD
or, BC/5.7 = 5.4/3.8
BC = 5.4 x 5.7 / 3.8
= 54×57 / 38 x 10
= 8.1 cm.
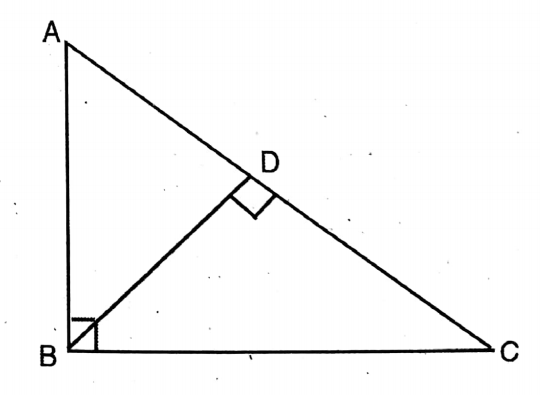
Question 3. In the adjoining figure, ABC = 90° and BD AC; if BD = 8 cm and AD = 4 cm, then let us write the length of the CD.
Solution:
Given
In the adjoining figure, ABC = 90° and BD AC; if BD = 8 cm and AD = 4 cm
ΔABD ~ ΔBDC
∴ BD² = AD X AC
or, (8)² = 4 x AC
∴ AC = 8×8 / 4
= 16 cm.
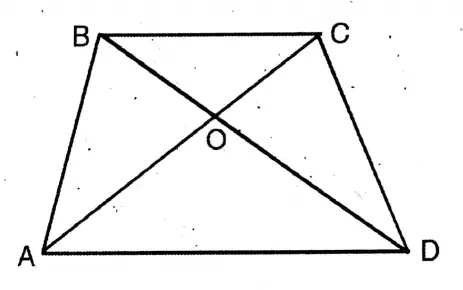
Question 4. In trapezium ABCD, BC || AD and AD = 4 cm. The two diagonals AC and BD intersect at point O in such a way that, AO/OC = DO/OB = 1/2 Let us calculate the length of BC.
Solution.
Given
In trapezium ABCD, BC || AD and AD = 4 cm. The two diagonals AC and BD intersect at point O in such a way that, AO/OC = DO/OB = 1/2
From ΔAOC & ΔAOD, we get
BO/OD = OC/AD = 1/2
Remaining BC/AD = 1/2
or, AD/BC = 1/2
or, 4/BC = 1/2
.. BC = 4 X 2
= 8
length of BC = 8
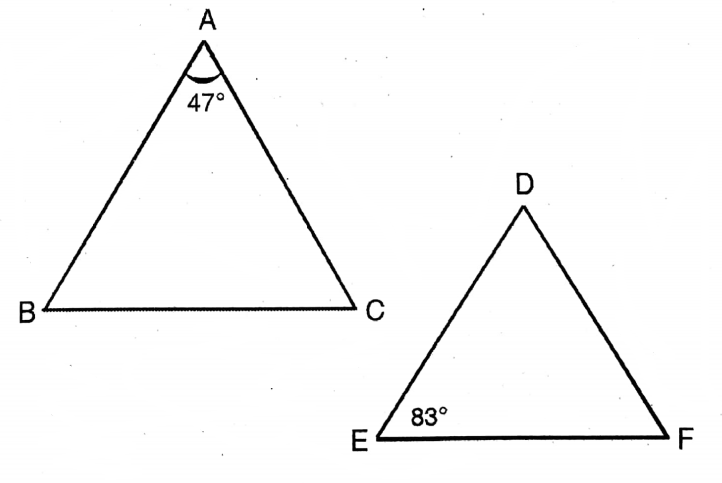
Question 5. ΔABC = ΔDEF and in AABC and ADEF, the corresponding sides of AB, BC, and CA are DE, EF, and DF respectively; if ∠A = 47° and ∠E 83°, then let us write the value of Z.
Solution.
Given
ΔABC = ΔDEF and in AABC and ADEF, the corresponding sides of AB, BC, and CA are DE, EF, and DF respectively; if ∠A = 47° and ∠E 83°
ΔABC ~ ΔDEF
In ΔABC, 47° ∠B + LC = 180°
& ∠B & ∠E are corresponding angles.
∴ ∠B = 83°
∴ ∠F = ∠C = 180° – (83° + 47°)
= 180°-130°
= 50°
∴ ∠C = 50°
