West Bengal Board Class 10 Math Book Solution In English Chapter 20 Trigonometry Concept Of Measurement Of Angle Exercise 20.1
Question 1. I am observing that I have got a right-angled triangle whose ZACB is an ![]() angle [acute/obtuse]
angle [acute/obtuse]
Answer. Acute.
Question 2. If any rotating ray rotates an angle of 30° more after two successive complete anticlockwise rotations from its initial position centering at its end, in that case, let us calculate the measurement of the angle that it will be.
Answer.
Given
If any rotating ray rotates an angle of 30° more after two successive complete anticlockwise rotations from its initial position centering at its end, in that case
The required measurement of angle = 2 x 360° + 30° = 750°
If any rotating ray rotates an angle of 45° more after three successive complete anticlockwise rotations, then in that case, let us calculate what will be the measurement of the angle
= 3 x 360° + 45° = 1125°
Read and Learn More WBBSE Solutions For Class 10 Maths
Question 3. We have got a relation between the units of two systems.

Application 1. The values of two angles of a triangle in the Sexagesimal system are 75° and 45° respectively; let us determine the value of the third angle in a circular system.
Solution:
Given
The values of two angles of a triangle in the Sexagesimal system are 75° and 45° respectively
Let, in ΔABC, ∠ABC = 75° and ∠ACB = 45°
∴ <BAC 180° (75° + 45°) = 60°
Again, 180° = π, .. 60°= π/3
:. The required value of the third angle in a circular system is π/3
Application 2. If the Sexagesimal values of two angles of a triangle are 65° and 85° respectively, let us determine the Circular value of the third angle.
Solution:
Given
If the Sexagesimal values of two angles of a triangle are 65° and 85° respectively,
3rd angle 180° = (65° + 85°) = 180° – 150° = 30°
Circular value of 3rd angle = 30° x π/180° =π/ 6
West Bengal Board Class 10 Math Book Solution In English
Application 3. A rotating ray rotates 30° more after two complete rotations in an anticlockwise direction; let us determine the Sexagesimal and Circular value of the angle.
Solution:
Given
A rotating ray rotates 30° more after two complete rotations in an anticlockwise direction
Since the ray is rotating anticlockwise direction,
∴ The angle will be negative [positive/negative]
For one complete rotation of the rotating ray, a 360° angle is formed.
∴ For 2 complete rotations, the angle will be 2 360° = 720°
Since after 2 complete rotations, it rotates 30° more angle,
So, the sexagesimal value of the angle is 720° + 30° = 750°
Again, 180° = π,
∴ 750° = (750/180 π) = 4 1/6 π

Application 4. I express 40° 16′ 24″ into radian.
Solution: 40° 16′ 24″
=40° +16+ 24″
=40° + 16′ + (24/60)‘ [ 60″ = 1′]
=40° + 16′ + 2‘/5 = 40° + (16 + 2/5)‘
= 40° + 82‘/5
= 40° + 6041°/150
Since 180°= π
∴ 6041/150 = Π/180 x 6041/150 = 6041/27000π
Application 5. Let me express 22°30′ into radian.
Solution: 22°30′
= 22° +(30/60)°
= 22° + (1/2)°
= 45°/2
Circular measurement = π/180 x 45/2 = πc/8
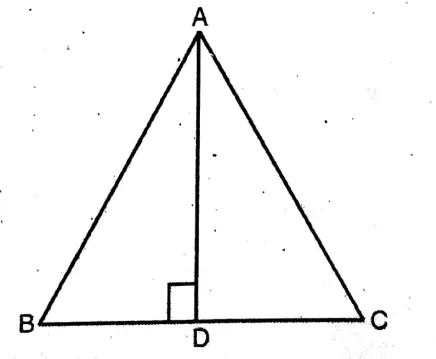
Application 6. I have drawn an equilateral triangle ABC. The line joining mid-point D of BC and the vertex A is AD; let us write by calculating, the circular value of ZBAD.
Hints: In the equilateral triangle ABC, ∠BAC = 60° and the median of an equilateral triangle is the bisector of the corresponding angle.
∴ ∠BAD = 30°
Solution: ΔABC is an equilateral triangle
∴ <BAC = ∠ABC = ∠ACB = 60°
∴ AD is a median of the ΔABC
∴ AD ⊥ BC ∴∠ADB = 90°
In ΔABD, ∠ABD = 60° & ZADB = 90°
∴ ∠BAD = 180° – (90° + 60°)
= 180° – 150°
= 30°
∴ Circular measure of BAD = π x 30° = π/6 radian.
Application 7. If the length of the radius of a circle is 6 cm, then let us write by calculating, the circular value of an angle which is subtended by an arc of 15 cm in length at the center.
Solution: Here the length of the arcs is 15 cm & radius is r = 6 cm.
∴ s=re
15= 6 x 0
∴ θ= 15/6 = 5/2 = radian.
Application 8. Let us write the value of the complementary angle of 27°27’27” in the sexagesimal system.
Solution: Let θ be the complementary angle of 27°27’27”
∴ θ=90°-27°27’27” here 90° = 89°59’60”
= 62°3233
= – 27°27’27” / θ = 62°32′33′′
∴ Complementary angle of 27°27’27” is 62°32’33”
Application 9. Let us write the supplementary angle of 85°32′36′′ in the sexagesimal system.
Solution: Let α be the supplementary angle of 85°32’36”
∴ α= 180° – 85°32’36”
= 94°27’24” here 180° = 179°59’60”
85°32’36” /94°27’34”
∴ Supplementary angle of 85°32’36” is 94°27’24”
Question 1. Let us express the following into degrees, minutes, and seconds.
1. 832′

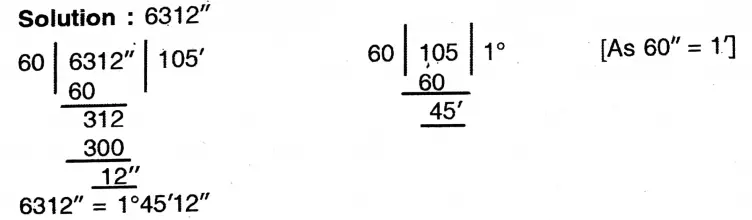
2. 6312″
3. 375″
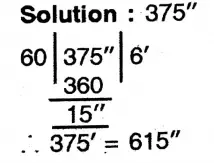
4. 27 (1/12)º
Solution: 271/12 °
= 27° + 1/12 °
= 27° + (1/12 x 60)‘
= 27°5′
271/12 °= 27°5′
5. 72. 04°
Solution: 72. 04°
= 72° + (0.04)°
= 72° + (0.04 60)’
= 72° + 2.4′
= 72°+2′ + (0.4 × 60)”
= 72°2′24′′
72. 04°= 72°2′24′′
Question 2. Let us determine the circular values of the following
1. 60°
Solution: 60°
πc/180 x 60
= πc/3 [as 180°=πc [.. 1° – Π/180 °]
2. 135°
Solution: 135°
= π/180 x 135c
=3πc/5
135°=3πc/5
3. – 150°
Solution: -150°
= -π/180 x 135c
= -5πc/6
-150°= -5πc/6
4. 72°
Solution: 72°
Π/180 x 72° = 2πc/5
72° = 2πc/5
5. 22°30′
Solution: 22°30′
= 22 1/2 °
= 45°/2
= Π/180 x 45c/2
= πc/8
22°30′ = πc/8
6. – 62°30′
Solution: 62°30′
= -62 1/2 °
= 125°/2
= Π/180(-125/2)c
= -25πc/72
62°30′ = -25πc/72
7. 52°52’30”
Solution: 52°52’30”
= 52°+ 52 1/2‘
= 52° + 105‘ /2
= 52° + 105/2 x 1/6 °
= 52° + 7/8 °
= (416+7 / 8)°
= 423° / 8
= π/8 x 423c/ 8 = 47c/ 64
52°52’30” = 47c/ 64
8. 40°16’24”
Solution: 40°16’24”
= 40° + 16′ + (24/60)°
= 40° + 16′ + 2’/5
= 40° + 82‘/5
= 40° + (82/5 x 1/60)°
= 40° + (41/150)°
= 6041° / 150
= π/180 x 6041c/150
= 6041πc/27000
40°16’24” = 6041πc/27000
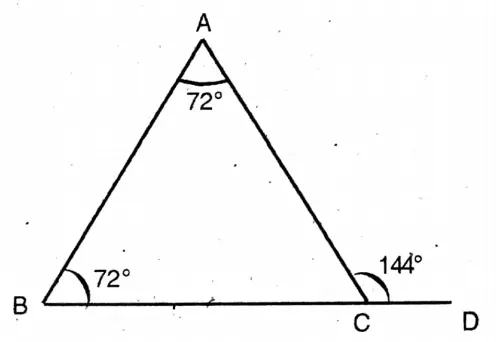
Question 3. In ΔABC, AC = BC, and BC is extended up to point D. If ∠ACD = 144°, then let us determine the circular value of each of the angles of AABC.
Solution:
Given
In ΔABC, AC = BC, and BC is extended up to point D. If ∠ACD = 144°
∠A = <BAC = 72°
=π/180 x 72° = 2πc/5
∠B =∠ABC = 72° = 2πc/5
∠C = ∠ACB = 36° = π/180 × 36 radian = π/5 radian
Question 4. If the difference between two acute angles of a right-angled triangle is 2π/5 then let us write the sexagesimal values of the two angles.
Solution:
Given
If the difference between two acute angles of a right-angled triangle is 2π/5
2π/5 radian = 2×180°/5
= 72°
Let one acute angle = x° & other acute angle = y°
∴ x + y = 90°
& x – y = 72°
2x = 162°
∴ X = 81° ∴ y 90°-81° = 9°
∴ Sexagesimal value of one angle = 81° & other angle = 9°
Question 5. The measure of one angle of a triangle is 65° and another angle is π/12; let us write the sexagesimal value and circular value of two angles.
Solution:
Given
The measure of one angle of a triangle is 65° and another angle is π/12
One angle of the triangle = 65°
another angle of the triangle = π/12
= 180/12
= 15°
∴ Third angle = 180° – (65° + 15°)
= 180° – 80° = 100°
= 100 πc/180 = 5π/9 radian.
∴ Sexagesimal value of the third angle = 100°
& circular value of the third angle = 5π/9 radian.
Question 6. If the sum of two angles is 135° and their difference is Π/12; then let us determine the sexagesimal value and circular value of two angles.
Solution:
Given
If the sum of two angles is 135° and their difference is Π/12
Let one angle = x°
& the other angle = y°
According to the problem, x + y = 135°
& x-y= Π/12
= 15°
Adding 2x = 150°
∴ x = 75°
∴ y = 135 – x = 135-75 = 60°
∴ Sexagesimal value of 1st angle = 75°
& Sexagesimal value of 2nd angle = 60°
Again, circular value of 1st angle: Π/180 × 75 = 5Π/12 radian.
& Circular value of 2nd angle = Π/180 x 60
= Π/3 radian.
Question 7. If the ratio of three angles of a triangle is 2:3: 4, then let us determine the circular value of the greatest angle.
Solution: The ratio of the three angles of a triangle is 2: 3:4
∴ Let the value of 1st angle = 2x°
& value of 2nd angle = 3x°
& the value of 3rd angle = 4x°
∴ 2x + 3x + 4x = 180°
∴ 9x = 180
∴ X = 180/9 = 20°
∴ The value of the greatest angle = 4x= 4 x 20° = 80°
= Π/180 x 80 = 4π/9 radian.
Question 8. The length of a radius of a circle is 28 cm. Let us determine the circular value of the angle subtended by an arc of 5.5 cm in length at the center of this circle.
Solution: Radius of the circle = 28 cm.
∴ Circumference = 2πr = 2 × 22/7 x 28 cm = 176 cm.
We know, the circumference makes an angle of 27 at the center
Here 176 cm arc can make an angle of 2π at the center
∴ 5.5 cm arc can makes an angle = 2Π/176 x 55/10 = Π/16 radian.
Question 9. The ratio of two angles subtended by two arcs of unequal lengths at the center is 5:2 and if the sexagesimal value of the second angle is 30°, then let us determine the sexagesimal value and the circular value of the first angle.
Solution:
Given
The ratio of two angles subtended by two arcs of unequal lengths at the center is 5:2 and if the sexagesimal value of the second angle is 30
Let the sexagesimal value of the 1st angle = x°
∴ x°: 30° = 5:2
or, x/30 = 5/2
or, x/30 = 5/2
or, 2x = 5 x 30 .. x = 5 x 30 / 2 = 75°
= Π/180 × 75 = 5π/12 radian.
∴ The sexagesimal value of the 1st angle = 75°
& the circular value of the 1st angle
=5Π / 12 radian.
Question 10. A rotating ray makes an angle -5 1/12 π. Let us write by calculating, in which direction the ray has completely rotated and thereafter what more angle it has produced.
Solution: As the angle is negative, the ray is moving in a clockwise direction.
Now -5 1/12 Π =
= -61/12 Π
= -61/12 x 180
= -61 x 15
= -915°
= (-2x 360+ 195)
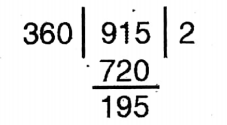
∴ The ray will move 2 complete revolutions in a clockwise direction & makes an angle of 195°.
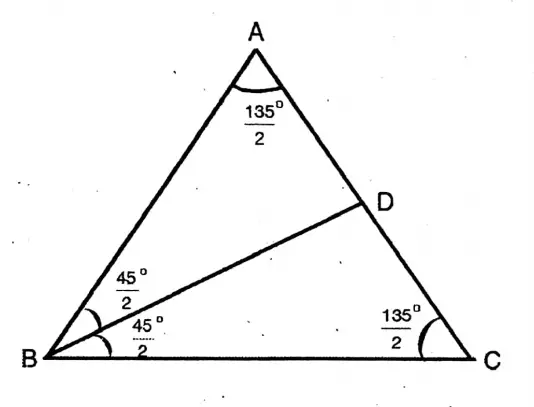
Question 11. I have drawn an isosceles triangle ABC whose included angle of two equal sides ABC = 45°; the bisector of ABC intersects the side AC at point D. Let us determine the circular values of ∠ABD,∠BAD, ∠CBD, and ∠BCD.
Solution: ABC is an isosceles triangle, AB = AB
Whose ∠ABC = 45°
∠BAC = ∠ACB
= 180°-45° / 2 = 135 / 2
&∠CBD = 45° /2
∠BCD = ∠BCA = 135° /2
Now 45° / 2
= 45/2 X π/180
= π/8
∴∠ABC = 45°/2 = π/8 ; ∠BAD =135°/2 = 3 π/8
∠CBD = 45°/2 = π/8; ∠BCD = 135°/2 = 3 π/8
Question 12. The base BC of the equilateral triangle ABC is extended upto the point E so that CE = BC. By joining A, and E, let us determine the circular values of the angles of AABC.
Solution:
Given
The base BC of the equilateral triangle ABC is extended upto the point E so that CE = BC. By joining A, and E
ABC is an equilateral triangle
∴ Each internal angle of the triangle = 60°
Side BC is extended to E
Such that BC= CE
Join AE,
Find the circular value of the angles of AACE
As ∠ACB=60° ∴ ∠ACE = 120°=120 π/180
= 2π/3
Again in ΔACE, ∠ACE = 120° & as AC = CE
∴ ∠CAE = ∠AEC = 180 – 120 / 2 = 30°
∴ ∠CAE 30° = π/180 X 30° = π
& ∠AEC = 30° = π/180 x 30° = π/6
Question 13. If the measures of three angles of a quadrilateral are π/3, 5π/3, and 90° respectively, then let us determine and write the sexagesimal and circular values of the fourth angle.
Solution:
Given
If the measures of three angles of a quadrilateral are π/3, 5π/3, and 90° respectively,
1st angle = π/3 = 180°/3 = 60°
2nd angle = 5π/6 = 5×180°/6 = 5 X 30 = 150°
3rd angle 90°
∴ 4th angle 360° = (60° + 150° +90°)
360° – 300° = 60° = 60 x π/180 = πc/3
WBBSE Class 10 Maths Solutions Chapter 20 Trigonometry Concept Of Measurement Of Angle Exercise 20.1 Multiple Choice Questions
Question 1. The endpoint of the minute hand of a clock rotates in 1 hour
1. π/4 radian
2. π/2radian
3. π radian
4. 2л radian
Solution: The endpoint of the minute hand of a clock rotates in 1 hour = 360° = 2π radian.
Answer. 4. 2π radian
Question 2. π/2 radian equals to
1. 60°
2. 450°
3. 90°
4. 30°
Solution: π/6 = 180°/6
= 30°
Answer. 4. 30°
Question 3. The circular value of each internal angle of a regular hexagon is
1. π/3
2. 2π/3
3. π/6
4. π/4
Solution: The circular value of each internal angle of a regular hexagon
= (180°- 360/6) x π/180 = 120 x π/180 = 2π/3
Answer. 2. 2π/3
Question 4. The measurement of 0 in the relation to s = re is determined by
1. Sexagesimal system
2. Circular system
3. Those two methods
4. None of these
Answer. 2. Circular system
Question 5. In cyclic quadrilateral ABCD, if A = 120°, then the circular value of C is
1. Π/3
2. Π/6
3. Π/2
4. 2π/3
Solution: In cyclic quadrilateral ABCD, if A = 120° then the circular value of C
= (180°- 120°) x π
= 60 x π/180
= π/3
Answer. 1. Π/3
WBBSE Class 10 Maths Solutions Chapter 20 Trigonometry Concept Of Measurement Of Angle Exercise 20.1 True Or False
1. The angle, k formed by rotating a ray centering its endpoint in an anticlockwise direction is positive.
Answer: True
2. The angle, formed for completely rotating a ray twice by centering its endpoint is 720°.
Answer: False
Chapter 20 Trigonometry Concept Of Measurement Of Angle Exercise 20.1 Fill In The Blanks
1. π radian is a Constant angle.
2. In the sexagesimal system 1 radian equals 57°16′22″ (approx)
3. The circular value of the supplementary angle of the measure 3Π/8 is 5π/8
WBBSE Class 10 Maths Solutions Chapter 20 Trigonometry Concept Of Measurement Of Angle Exercise 20.1 Short Answers
Question 1. If the value of an angle in degree is D and in radian is R; then let us determine the value of R/D
Solution.
Given
If the value of an angle in degree is D and in radian is R
180° = π radian
1° = π/180 radian
∴ R° = л/180 D radian = Dл/180 ..лD/180 = R
or, 180R = лD
or, R/D = π/180
Question 2. Let us write the value of the complementary angle of the measure 60°35′15′′.
Solution. 90° 89°59’60”
-63°35’15” / 26°24’45”
The complementary angle of the measure 63°35’15” is 26°24’45”
Question 3. If the measures of two angles of a triangle are 65°56′55′′ and 64°3’5″, then let us determine the circular value of the third angle.
Solution.
Given
If the measures of two angles of a triangle are 65°56′55′′ and 64°3’5″,
1st angle = 65°56′55′′
2nd angle = 64°03′05′′
∴ Sum of two angles = 130°00’00”
Measure of 3rd angle = 180° – 130° = 50° = 50 x π/180 = 5π/18
Question 4. in a circle, if an arc of 220 cm in length subtends an angle of measure 63° at the center, then let us determine the radius of the circle.
Solution.
Given
in a circle, if an arc of 220 cm in length subtends an angle of measure 63° at the center
Let the radius of the circle = r cm.
∴ Circumference = 2πr = 2 x 22/7 r cm = 44r/7 cm.
Now 360° angle is formed by an arc of 44r/7 cm.
1° angle formed by arc by 44r / 7×360 cm.
63° angle formed by arc of 44r / 7×360 x x 63 cm = 11r/10 cm.
11r/10 = 220
∴ r = 220×10 / 11 = 200
∴ The radius of the circle is 200 cm = 2m.
OR, 180° = π
1° = π/180
63° = π/180 × 63 = 7π/20 radian
= 7/20 x 22/7
= 11/10 radian.
∴ S = rθ
or, 220 = r x 11/10
∴ r= 220 x 10 / 11
= 200cm
= 2m.
Question 5. Let us write the circular value of an angle formed by the endpoint of the hour hand of a clock in a 1-hour rotation.
Solution. In 12 hours angle produced by the hour hand of a clock is 2π radian
In 1 hour angle produced by the hour hand of a clock is 2π/12 = π/6 radian.
∴ Circular value of the angle = π/6 radian.
