WBBSE Class 10 Maths Solutions Chapter 22 Pythagoras Theorem Exercise 22.1
(4) Area of the region of the trapezium ABCD =1/2 (a+b) x (a+b)
Again, the area of the region of the trapezium
= area of DAE + area of CBE + area of CBE + area of DEC
Read and Learn More WBBSE Solutions For Class 10 Maths
Application 1. Taking different proper values of m and n, let us write the sides of two right-angled triangles.
Solution: In the case of a right-angled triangle, if two sides & the hypotenuse of the triangle are (m² – n²) units, 2mn units & (m²+n²) units
respectively then (m²- n²)² & (2mn)² = (m2+N2)²
Now let m = 10, n = 6
∴ LHS = (10262)² + (2.10.6)²
= (64)² + (120)²=4096 +14400 = 18496
RHS = (102 +62)² = (136)² = 18496
∴ LHS = RHS

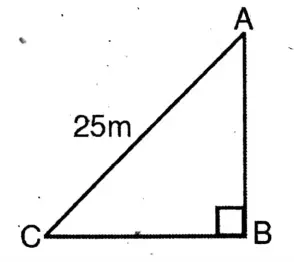
Application 2. In our garden, a ladder of 25 m in length is inclined to a guard wall at a height of 24 m above the ground. Let us write by calculating, the distance of the foot of the ladder from the guard wall.
Solution:
Given
In our garden, a ladder of 25 m in length is inclined to a guard wall at a height of 24 m above the ground.
Let the length of the ladder AC = 25 m, AB = 24 m,
Pythagoras’ theorem in right-angled triangle ABC, we get,
AB²+BC² = AC²
or, (24m)² + (BC)² = (25m)²
∴ BC = 7
or, BC² (25m)²- (24m)² = 49
The foot of the ladder is in 7m
distance from the guard wall.
“West Bengal Board Class 10 Maths Chapter 22 Pythagoras Theorem Exercise 22.1 solutions”
Application 3. If the lengths of two diagonals of a rhombus are 12 cm and 16 cm respectively, then let us write by calculating, the length of one side of this rhombus.
Hints:
Given
If the lengths of two diagonals of a rhombus are 12 cm and 16 cm respectively
The two diagonals of a rhombus bisect each other, perpendicularly.
∴ OA = 12/2 cm = ![]() cm, OB =
cm, OB = ![]() cm.
cm.
AOB is a right-angled triangle.
∴ From Pythagoras’ theorem, we get, AB²+ OB²
We know, the diagonals of a rhombus bisect each other perpendicularly.
∴ Let BD 16 cm. ∴ BO = OD = 8cm
& AC =12 cm. ∴ AO OC = 6 cm.
∴ ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
∴ BOC is a right-angled triangle.
BC = √BO² + CO²
= √82 +62
= √100
= 10 cm.


Application 4. If in ΔABC, ADL BC, let us prove that, AB²+ CD² = AC²+ BD²
Solution: To prove AB²+ CD² = AC² + BD²
In ΔABC, perpendicular drawn from
A, on BC, is AD.
∴ AD ⊥ BC
∴ ∠ADB = ∠ADC = 90°
From two right-angled triangles ABD & ADC,
AB² = AD² + BD²——-(1)
& AC² = AD²+ DC²———(2)
Subtracting (1) from (2), AB² – AC² = BD² – DC²
or, AB²+ CD² = AC²+ BD² Proved.

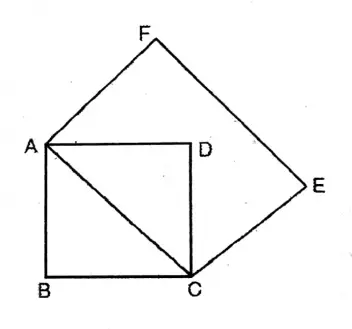
Application 5. Let us prove that the area of a square drawn on the diagonal of a square is twice of the area of that square.
Solution: Area of ABCD square = AD²
Area of ACEF square = AC²
In ΔACD, ∠ADC = 90°
AD = CD [Side of a square]
AC = √AD²+DC² = √AD²+DC² = AD √2
AC² = (AD √2)²= 2AD²
Question 1. If the followings are the lengths of the three sides of a triangle, then let us write by calculating, the cases where the triangles are right-angled triangles
1. 8 cm, 15 cm. and 17 cm
2. 9 cm, 11 cm, and 6 cm.
Solution: In a right angle triangle, (Perpendicular)² + (Base)² = (Hypotenuse)² Here,
(8)² + (15)² = (17)²
or, 64+ 225
= 289
∴ It is a right-angled triangle.
“WBBSE Class 10 Pythagoras Theorem Exercise 22.1 solutions explained”
Question 2. In the road of our locality there is a ladder of 15 m in length kept in such a way that it has touched Millis’ window at a height of 9 m above the ground. Now keeping the foot of the ladder at the same point of that road, the ladder is rotated in such a way that it touched our window situated on the other side of the road. If our window is 12 m above the ground, then let us determine the breadth of that road in our locality.
Solution:
Given
In the road of our locality there is a ladder of 15 m in length kept in such a way that it has touched Millis’ window at a height of 9 m above the ground. Now keeping the foot of the ladder at the same point of that road, the ladder is rotated in such a way that it touched our window situated on the other side of the road. If our window is 12 m above the ground
In ΔABE, BE2 (AE)²- (AB)²
= (15)² – (9)²
= 225-81
= 144
∴ BE = √144 = 12
In Δ EDC = EC² = ED² – CD²
=152 – 122
= 225-144
= 81
∴ EC = 9
∴ BC = BE + EC = 12+9 = 21 m.
∴ The breadth of the road = 21 m.

Question 3. If the length of one diagonal of a rhombus having a side of 10 cm length is 12 cm, then let us write, by calculating the length of the other diagonal.
Solution:
Given
If the length of one diagonal of a rhombus having a side of 10 cm length is 12 cm
The length of one diagonal of a rhombus of side 10 cm is 12 cm.
In △AOB, \(O B^2+O A^2=A B^2\)
Here, OB = \(\frac{12}{2}\) = 6 cm
& OA = 10cm.
∴ \(\mathrm{AO}^2=\mathrm{AB}^2-\mathrm{OB}^2\)
= \((10)^2-(6)^2\)
= 100 – 36 = 64
AO = √64 = 8

Question 4. I have drawn a triangle PQR whose ∠Q is a right angle. If S is any point on QR, let us prove that PS²+ QR² = PR²+ QS².
Solution: In a right-angled triangle PQR, ∠Q = 90°
S is any point in QR
To prove \(P S^2+Q R^2=P R^2+Q S^2\)
Proof: △PQS & △PQR are two right angled triangles.
∴ \(\mathrm{PS}^2=\mathrm{PQ}^2+\mathrm{QS}^2\)
\(P R^2=P Q^2+Q^2\)or, \(\mathrm{QR}^2=P R^2-\mathrm{PQ}^2\)
∴ \(P S^2+Q R^2=P Q^2+Q S^2+P R^2-P Q^2\)
= \(Q S^2+P R^2\)
∴ \(\mathrm{PS}^2+\mathrm{QR}^2=\mathrm{PR}^2+\mathrm{QS}^2\) Proved.
“WBBSE Class 10 Maths Exercise 22.1 Pythagoras Theorem problem solutions”
Question 5. Let us prove that the sum of squares drawn on the sides of a rhombus is equal to the sum of squares drawn on two diagonals.
Solution: AC & BD two diagonals of the rhombus ABCD, intersect each other at O.
To prove, \(A B^2+B C^2+C D^2+D A^2=A C^2+B D^2\)
We know the diagonals of a rhombus bisect each other perpendicularly.
i.e., AC ⊥ BD, & AO = OC & BO = OD
∴ △AOB, △BOC, △COD & △DOA
are four right angled triangles.
\(\mathrm{AB}^2=\mathrm{OA}^2+\mathrm{OB}^2 ; \mathrm{BC}^2=\mathrm{OB}^2+\mathrm{OC}^2\) \(\mathrm{CD}^2=\mathrm{OC}^2+\mathrm{OD}^2 ; A D^2=\mathrm{OD}^2+\mathrm{OA}^2\) \(\mathrm{AB}^2+\mathrm{BC}^2+\mathrm{CD}^2+\mathrm{AD}^2=\mathrm{OA}^2+\mathrm{OB}^2+\mathrm{OB}^2+\mathrm{OC}^2+\mathrm{OC}^2+\mathrm{OD}^2+\mathrm{OD}^2+\mathrm{OA}^2\)= \(2\left(\mathrm{OA}^2+\mathrm{OB}^2+\mathrm{OC}^2+\mathrm{OD}^2\right)\)
= \(2\left(\mathrm{OA}^2+\mathrm{OC}^2+\mathrm{OB}^2+\mathrm{OB}^2\right)\)

Question 6. ABC is an equilateral triangle. AD is perpendicular on the side BC; let us prove that, AB²+ BC²+ CA² = 4AD².
Solution: In the equilateral triangle ABC, AD is perpendicular to BC.
To prove \(A B^2+B C^2+C A^2=4 A D^2\)
Proof: In △ABC, AD ⊥ BC ∴ BD = DC
△ABD & △ACD are two right angled triangles
\(\mathrm{AB}^2=\mathrm{AD}^2+\mathrm{BD}^2 \& \mathrm{CA}^2=\mathrm{AD}^2+\mathrm{DC}^2\)\(A B^2=A D^2+B D^2=A D^2+D C^2\) [∵ BD = DC]

Question 7. I have drawn a right-angled triangle ABC whose A is a right angle. I took two points P and Q on the sides AB and AC respectively. By joining P, Q; B, Q and C, P, let us prove that BQ²+ PC² = BC² + PQ².
Solution:
Given
I have drawn a right-angled triangle ABC whose A is a right angle. I took two points P and Q on the sides AB and AC respectively.
To prove BQ²+ PC² = BC² + PQ²
△ABC, △ABQ, △APQ are all right angled triangles
where ∠A = 90°
\(\mathrm{BC}^2=\mathrm{AB}^2+\mathrm{AC}^2\) \(B Q^2=A Q^2+A B^2 ; P C^2=A P^2+A C^2 ; P Q^2=A P^2+A Q^2\)Now, \(B Q^2+P C^2=A Q^2+A B^2+A P^2+A C^2\)
& \(\mathrm{BQ}^2+\mathrm{PQ}^2=A B^2+A C^2+A P^2+A Q^2=A Q^2+A B^2+\mathrm{AP}^2+\mathrm{AC}^2\)
BQ²+ PC² = BC² + PQ². Proved

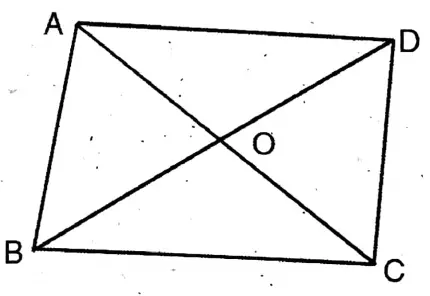
Question 8. If two diagonals of a quadrilateral ABCD intersect each other perpendicularly, then let us prove that AB²+ CD² = BC² + DA².
Solution: To prove, AB²+ CD² = BC² + DA²
AC & BD, the two diagonals of the quadrilateral ABCD, intersect each other perpendicularly at O.
∴ △AOB, △BOC, △COD & △DOA are all right angled triangles.
∴ \(\mathrm{AB}^2=\mathrm{OA}^2+\mathrm{OB}^2\)
\(\mathrm{BC}^2=\mathrm{OB}^2+\mathrm{OC}^2\) \(\mathrm{CD}^2=\mathrm{OC}^2+\mathrm{OD}^2\) \(\mathrm{DA}^2=\mathrm{OD}^2+\mathrm{OA}^2\)∴ \(A B^2+C D^2=O A^2+O B^2+O C^2+O D^2\)
& \(\mathrm{BC}^2+\mathrm{DA}=\mathrm{OB}^2+\mathrm{OC}^2+\mathrm{OD}^2+\mathrm{OA}^2\)
∴ AB²+ CD² = BC²+ DA². Proved.
“Class 10 WBBSE Maths Exercise 22.1 Pythagoras Theorem step-by-step solutions”
Question 9. I have drawn a triangle ABC whose height is AD. If AB > AC, let us prove that, AB² – AC² = BD² – CD².
Solution: In ΔABC, AD is the height of the AABC & AB > AC.
To prove, \(A B^2-A C^2=B D^2-C D^2\)
Proof: AD is the height of ABC, AD ⊥ BC.
△ABD & △ACD are two right angled triangle
\(A B^2=A D^2+B D^2\)& \(A C^2=A D^2+C D^2\)
\(A B^2-A C^2=A D^2+B D^2-A D^2-C D^2\)= \(B D^2-C D^2\)
\(A B^2-A C^2=B D^2-C D^2\) Proved.

Question 10. ABC is an isosceles triangle ‘whose C is a right angle. If D is any point on AB, then let us prove that AD²+ DB² = 2CD².
Solution:
Given
ABC is an isosceles triangle ‘whose C is a right angle. If D is any point on AB
To prove AD²+ BD² = 2CD²
From point D, DE & DF are two perpendicular on BC
& CA respectively,
& ∠DFC = 1 right angle
& ∠DEC = 1 right angle
In CEDF quadrilateral,
∠FCE = ∠DFC = ∠DEC = 1r. angle
In CEDF rectangle, CF || ED
∴ CA || ED & ∠ADB is the intercept
∴ ∠CAD = ∠EDB (corresponding)
∴ ∠EDB = ∠DBE ∴ DE = BE
as CAB = ABC, △ABC is an isosceles triangle.
∴CF = DE = BF: Now, ΔADF, ΔBDE & ΔCDE are all right angles.
∴ AD² = AF² + FD²;
DB² = BE² + DE²;
CD² = CE² + DE²
Now, AD² + DB² = AF² + FD²+ BE² + DE²
= CE²+ CE² + DE² + DE² = 2CE² + 2DE²
=2(CE² + DE²) = 2CD² [AC – CF BC – BE, AF = CE & BE = DE]
= AD²+ DB²
2CD² Proved.

Question 11. In the triangle ABC, ZA is the right angle; if CD is the median, let us prove that BC² = CD² + 3AD².
Solution :
Given
In the triangle ABC, ZA is the right angle; if CD is the median
To prove BC² = CD² + 3AD²
In △ABC, CD is median AD = DB.
△CAB & △CAD are right angled triangles.
\(B C^2=A B^2+A C^2 \& C D^2=A D^2+A C^2\) \(A C^2=C D^2-A D^2\) \(B C^2=(2 A D)^2+C D^2-A D^2\)= \(4 A D^2+C D^2-A D^2\)
= \(3 A D^2+C D^2\)
∴ \(\mathrm{BC}^2=\mathrm{CD}^2+3 A D^2\) Proved.

Question 12. From point O within a triangle ABC, I have drawn the perpendiculars OX, OY, and OZ on BC, CA, and AB respectively. Let us prove that AZ + BX2+ CY² = AY² + CX² + BZ².
Solution:
Given
From point O within a triangle ABC, I have drawn the perpendiculars OX, OY, and OZ on BC, CA, and AB respectively.
To prove, AZ²+ BX²+ CY² = AY² + CX²
AAZO; ABZO; ABXO; ACXO; ACYO; AAYO are all right angle triangles.
∴ AO² = AZ² – ZO² or, AZ²2 = AO² – ZO²
CX² = CO²-OX² or, CY² = CO² – YO²
or, AY² = AO² – OY²
∴ AZ² + BX² + CY² – (AY²+ CX² + BZ²)
= (AO²-OZ + BO²-OX²+ CO²-OY²)-(AO²-OY² + CO² – OX² + BO² – OZ²)
=(AO² – AO²)+(OZ²-OZ²) + (BO² – BO²)+ (OX² – OX²) + (CO²- CO²)+ (OY² – OY²) = 0
∴ AZ²+ BX²+ CY² = AY²+ BZ²+ CX² Proved.

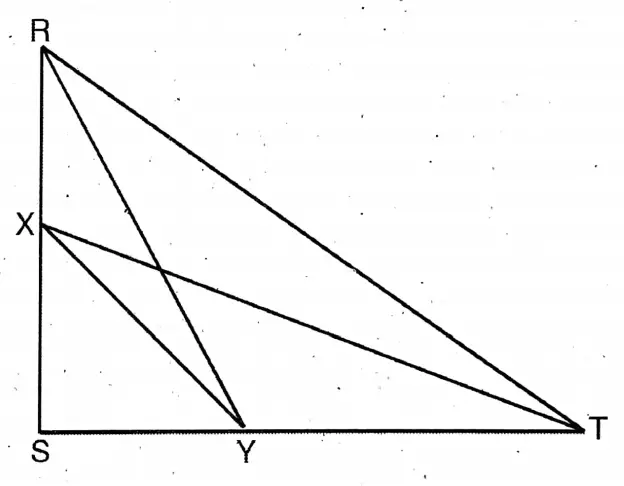
Question 13. In ARST, ZS is a right angle. The midpoints of the two sides RS and ST are X and Y respectively; let us prove that, RY² + XT² = 5XY².
Solution: To prove, RY² + XT² = 5XY²
Proof: From △RSY, \(R Y^2=R^2+S Y^2\)
From △XST, \(\mathrm{XTT}^2=\mathrm{ST}^2+\mathrm{SX}^2\)
∴ \(R Y^2+X T^2=\left(R S^2+S T^2\right)+\left(S Y^2+S X^2\right)\)
= \(R T^2+\left(\frac{1}{2} S T\right)^2+\left(\frac{1}{2} R S\right)^2\)
as \(S Y=\frac{1}{2} S T \& S \dot{x}^2=\frac{1}{2} R S\)
= \(R \mathrm{~T}^2+\frac{1}{4} R \mathrm{~T}^2\)
as \(X Y=\frac{1}{2} R T\)
∴ From (1) RY²+ XT² = 5XY² Proved.
WBBSE Solutions Guide Class 10 Maths Chapter 22 Pythagoras Theorem Exercise 22.1 Multiple Choice Questions
Question 1. A person goes 24 m west from a place and then he goes 10 m north. The distance of the person from starting point is
1. 34 m.
2. 17 m.
3. 26 m.
4. 25 m.
Solution: The distance of the person from the starting point
= √242+102 = √576+100 = √676 = 26 m.
Answer. 3. 26 m.
“WBBSE Class 10 Chapter 22 Pythagoras Theorem Exercise 22.1 solution guide”
Question 2. If ABC is an equilateral triangle and AD BC, then AD2 =
1. 3/2DC²
2. 2DC²
3. 3DC²
4. 4DC²
Solution: AD (Height of equilateral triangle)
= (√3/2)Side
= 3/4 Side²
= 3/4 (BC)²
= 3/4 × (2DC)²
=3/4 x 4DC²
= 3DC²
Answer. 3. 3DC²

Question 3. In an isosceles triangle ABC, If AC BC and AB² = 2AC², then the measure of ZC is
1. 30°
2. 90°
3. 45°
4. 60°
Solution: Here, AC BC & AB² = 2AC²
∴ AB² = AC² + BC² ∴ ZC = 90°
Answer. 2. 90°

Question 4. Two rods of 13 m in length and 7 m in length are situated perpendicularly on the ground and the distance between their foots is 8 m. The distance between their top parts is
1. 9 m.
2. 10 m.
3. 11 m.
4. 12 m.
Solution: Here AC² = AB²+ BC²
= 62+82 = 100
∴ AC = 10 m.
Ans. 2. 10 m.

“West Bengal Board Class 10 Maths Exercise 22.1 Pythagoras Theorem solutions”
Question 5. If the lengths of two diagonals of a rhombus are 24 cm and 10 cm, the perimeter of the rhombus is
1. 13 cm.
2. 26 cm.
3. 52 cm.
4. 25 cm.
Solution: ∴ BD = 24 cm. ∴ DO = 12 cm.
AC = 12 cm. CO = 5 cm.
DC² = AO² + OC² = 122 + 52
= 144 +25
= 169
∴ DC = √169
= 13 cm.
:. Perimeter = 4 x 13 cm.
= 52 cm.
Answer. 3. 52 cm.

WBBSE Class 10 Maths Solutions Pdf In English Chapter 22 Pythagoras Theorem Exercise 22.1 True Or False
1. If the ratio of the lengths of three sides of a triangle is 3: 45, then the triangle will always be a right-angled triangle.
Answer: True
2. If in a circle of radius 10 cm in length, a chord subtends a right angle at the center, then the length of the chord will be 5 cm.
Answer: False
Fill In The Blanks
1. In a right-angled triangle, the area of a square drawn on the hypotenuse is equal to the area of the sum of squares drawn on the other two sides.
2. In an isosceles right-angled triangle if the length of each of two equal sides is 4 cm, then the length of the hypotenuse will be 8 cm.
3. In a rectangular figure ABCD, the two diagonals AC and BD intersect each other at point O, if AB = 12 cm, AP = 6.5, then the length of BC is 15 cm.
WBBSE Class 10 Maths Solutions Chapter 22 Pythagoras Theorem Exercise 22.1 Short Answer
Question 1. In AABC, if AB = (2a-1) cm AC = 2√2a cm. and BC= (2a + 1) cm, then let us write the value of <BAC.
Solution.
Given
In AABC, if AB = (2a-1) cm AC = 2√2a cm. and BC= (2a + 1) cm
AB = (2a – 1) cm.
AC = 2√2a cm.
BC (2a + 1) cm.
∴ AB²+ AC² = (2a-1)+(2√2a)²
= 4a² – 4a+1 + 8a
= 4a² + 4a + 1
= (2a + 1)²
O = BC²
∴ ∠BAC 90°

“Class 10 WBBSE Maths Exercise 22.1 solutions for Pythagoras Theorem”
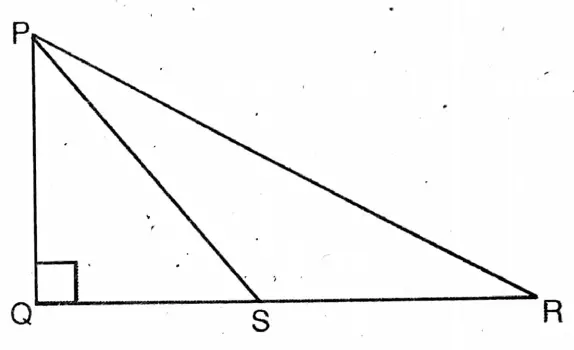
Question 2. In the adjoining figure, point O is situated within the triangle PQR in such a way that, POQ = 90°, OP = 6 cm, and OQ = 8 cm. If PR = 24 cm and ∠QPR = 90°, then let us write the length of QR.
Solution.
Given
In the adjoining figure, point O is situated within the triangle PQR in such a way that, POQ = 90°, OP = 6 cm, and OQ = 8 cm. If PR = 24 cm and ∠QPR = 90°,
As ∠POQ = 90°
∴ PQ² = OP² + OQ² = 62+ 82 = 100
∴ PQ = 10 cm.
Again, ∠QPR = 90°
∴ QR² = PQ²+ PR²
= 100+ 576
= 676
QR = √676
= 26 cm.

Question 3. point O is situated within the rectangular figure ABCD in such a way that OB = 6 cm, OD = 8cm, and OA = 5 cm. Let us determine the length of OC.
Solution. 5√3
Question 4. In the triangle, ABC the perpendicular AD from point A on side BC meets side BC at point D. If BD = 8 cm, DC = 2 cm, and AD = 4 cm, then let us write the measure of <BAC.
Solution.
Given
In the triangle, ABC the perpendicular AD from point A on side BC meets side BC at point D. If BD = 8 cm, DC = 2 cm, and AD = 4 cm,
∠ADB 90°
∴ AB² = AD²+ DB²
= 42+ 82
= 16+6480
AC² = CD²+ AD²
= 4+16
=20
∴ Here, BC² = (2+8)² (10)²
= 100
∴ AB²+ AC²=80+20
=100
∴ <BAC = 90°.

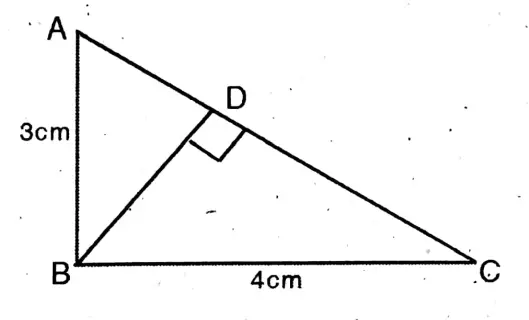
Question 5. In a right-angled triangle, ABC, ABC = 90°, AB = 3 cm, BC = 4 cm, and the perpendicular BD on the side AC from point B which meets the side AC at point D. Let us determine the length of BD.
Solution.
Given
In a right-angled triangle, ABC, ABC = 90°, AB = 3 cm, BC = 4 cm, and the perpendicular BD on the side AC from point B which meets the side AC at point D.
Here ABC ∼ BDC
AB/AC = BD/BC AC² = AB² + BC²
3/5 = BD/4
= 9+16
=25
∴ AC = √125
=5
∴ BD= 12/5
= 2.4 cm.
The length of BD = 2.4 cm.