Class 10 WBBSE Math Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.1
Application 3. 50 is an acute angle and if tan 5θ = tan (60° + θ), then let us determine the value of θ.
We shall remember: Generally,
1. sin 2 θ + 2 sineθ
2. sin α/sin ẞ =not α/β
and 3. sina +- sinẞ not = sin (α +- β)
These rules are applicable also in the cases of cosine, tangent, etc….. of an angle.
Solution: tan 5 θ = tan (60 + θ)
or, 5 θ = 60 + θ
or, 4 θ = 60°
∴ θ = 60°/4
θ = 15°

Read and Learn More WBBSE Solutions For Class 10 Maths
Application 5. It is a positive acute angle, and tan e = 8/15′ then let us determine the values of sine and cos θ and prove that sin20 + cos20 = 1.
Solution: ABC is a right-angled triangle whose ABC = 90° and ACB = θ
∴ tan θ = AB/BC = 8/15
Let, perpendicular AB = 8k units and base BC= 15k units [where k > 0]
AC² = AB² + BC²
= (8K)² + (15K)²
= 64K² + 225K²
= 289K²
∴ sin θ = AB/AC = 8k/17k
= 8/17
cos θ = base / hypotenuse 17k
∴ sin² θ+ cos² B = (8/17)² + (15/17)²
= 64/289 + 225/289
= 1
∴ sin2θ+ cos2θ = 1.
Application 6. If tan = 4/3, then let us show that, sin + cos = 7/5
Solution: tan θ = 4/3 ∴ perpendicular = 4k & base = 3k
∴ Hypotenuse = √(4k)² + (3k)²= √16k² +9k²
∴ sinθ + cosθ = 4k/5k + 3k/5k = 7k/5k = 7/5 proved.
Application 7. In ΔABC, ∠B is the right angle and the length of its hypotenuse is √13 units. If the sum of the lengths of the other two sides is 5 units, then let us determine the value of sin C + sin A.
Solution:
Given
In ΔABC, ∠B is the right angle and the length of its hypotenuse is √13 units. If the sum of the lengths of the other two sides is 5 units
In the right-angled triangle ABC, AC is the hypotenuse.
AB is perpendicular with respect to ∠C and BC is perpendicular with respect to ∠A.
∴ sin C + sin A = AB/AC = BC/AC
AB+BC / AC
= 5/√13
Alternative Proof: Let, AB = x unit,
BC = (5 – x) unit.
According to Pythagoras’ theorem, in a right-angled triangle ABC,
x² + (5-x)² = (√13)
or, x²+25+x-10x= 13
or, 2x²-10x+12= 0
or, x²-5x+6=0
or, x2-3x-2x+6=0
or, x(x-3)-2(x-3)=0
or, (x-3)(x-2)=0
Either, x-3=0 ∴ x = 3
Or, x-2=0 ∴ x = 2
If AB is 3 units, then BC (5 – 3) units = 2 units.
Hence, sin C = AB/AC= 3/√13
and sin A = BC/AC = 2/√13
∴ sin C+ sin A = 3/√13 + 2/√13 = 5/√13
Again, if AB 2 units, then BC= 3 units and then sin C + sin A = 5/√13
1. I have drawn a right-angled triangle ABC whose hypotenuse AB = 10 cm, base BC = 8 cm, and perpendicular AC = 6 cm. Let us determine the values of sine and tangent /ABC.
Solution:
Given
I have drawn a right-angled triangle ABC whose hypotenuse AB = 10 cm, base BC = 8 cm, and perpendicular AC = 6 cm.
Here base BC= 8 cm
& perpendicular AC = 6 cm.
∴ AB = √62 +82
= √100
= 10cm.
∴ sin ∠ABC = Perpendicular/hypotenuse
= 6/10 = 3/5
and tan ∠ABC = perpendicular/base
= 6cm/8 cm
= 6/8
= 3/4
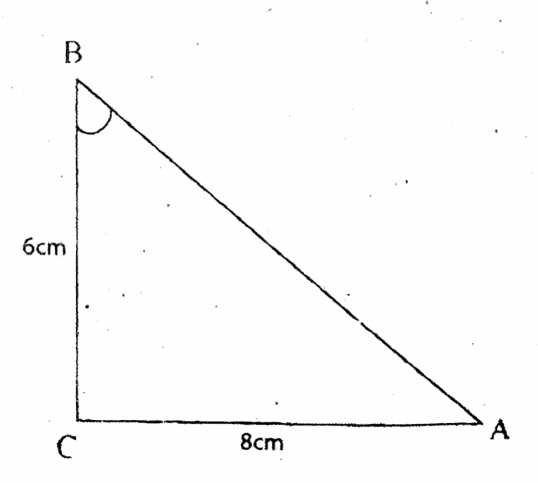
2. Soma has drawn a right-angled triangle ABC whose ABC= 90°, AB = 24 cm, and BC= 7 cm. By calculating, let us write the values of sin A, cos A, tan A, and cosec A.
Solution:
Given
Soma has drawn a right-angled triangle ABC whose ABC= 90°, AB = 24 cm, and BC= 7 cm.
Here AC²= AB²+ BC²
= (24)² + (7)²
= 576 +49 = 625
∴ AC = √625
= 25 cm.
sin A = BC/AC 7/25
cos A = BC/AC = 24/25;
tan A = BC/AC = 7/24
and cosec A = AC/BC = 25
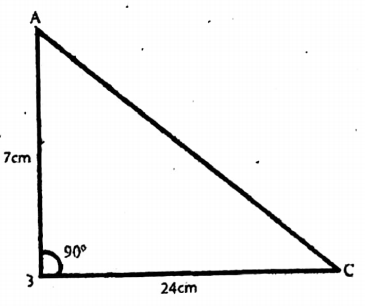
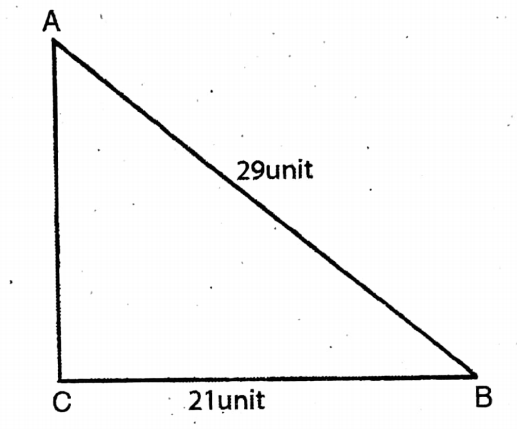
3. If in a right-angled triangle ABC, C = 90°, BC = 21 units, and AB = 29 units, then let us find the values of sin A, cos A, sin B and cos B.
Solution:
Given
If in a right-angled triangle ABC, C = 90°, BC= 21 units, and AB = 29 units,
Here AC² = AB² – BC²
= (29)²- (21)²
= 841-441= 400
∴ AC = √400 = 20 units.
sin A = BC/AC = 21/29
cos A = AC/BC = 20/29
sin B = AC/AB = 20/29
cos B = BC/AB = 21/29
4. If cos θ = 7/5 then let us determine the values of all trigonometric ratios of the angle 0.
Solution: As cos θ = 7/25
∴ Base AB 7 unit
Hypotenuse BC = 25 unit
AC² = BC²-AB² = (25)² – (7)²
= 625-49
= 576
= (24)²
∴ AC = 24 units
sin θ = P/H = AC/BC = 24/25 Here, let Perpendicular = P
cos θ = B/H = AB/BC = 7/25
tan θ = P/H = AC/AB = 24/7 Base B Hyptenuse = H
cot θ = B/P = AB/AC = 7/24
Sec θ = H/B BC/AB = 25/7
cosec θ = H/P = BC/AC = 25/24
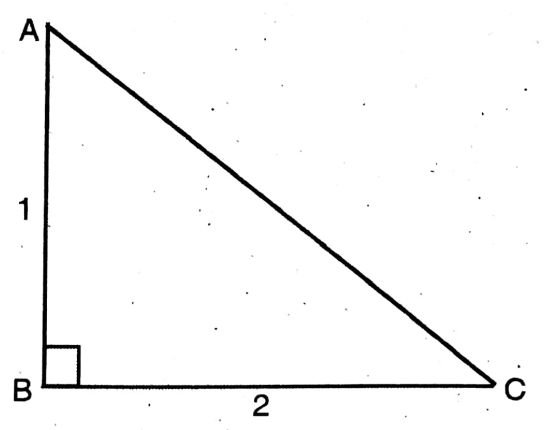
5. If cos θ = 2, then let us determine the values of tan e and sec e and show that 1 + tan²θ = sec² θ.
Solution: Here cote = 2 = 2/1 Base/Perpendicular = 2/1
∴ AC²= AB² + BC²
= (1)² + (2)²
∴ AC = √5
∴ tan e = P/B =1/2
Sece H/B = √5/2
L.H.S. = 1+tan20
= 1+(1/2)²
= 1+1/4
= 5/4
= (√5/2)²
= sec² θ
= R.H.S.
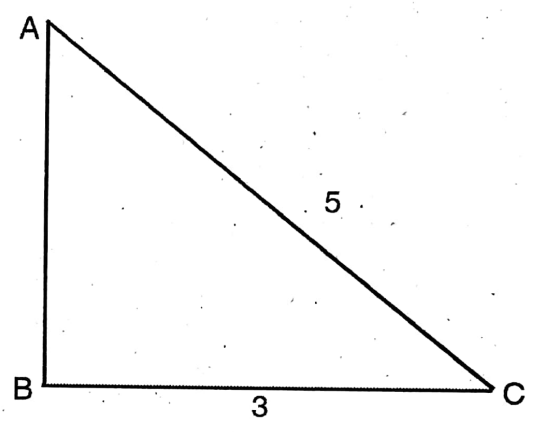
6. If cos θ 0.6, then let us show that (5sinθ – 3tanθ) = 0.
Solution: cos θ = 6/10 = 3/5 = B/H
∴ AB² = AC²-BC²
= (5)²- (3)²
=25 – 9
= 16
∴ AB = √16
= 4
L.H.S = 5 sinθ – 3 tanθ
= 5 x 4/5 – 3 x 4/3
=4-4
=0 R.H.S.
7. If cot A = 4/7.5 then let us determine the values of cos A and cosec A and show that 1+ cot² A = cosec² A.
Solution: cot A = 4/7.5 = B/P
∴ AB = 4, BC = 7.5
AC² = AB²+ BC²
=(4)² + (7.5)²
= 16+ 56.25
= 72.25
∴ AC = √72.25
= 8.5 = H.
cos A = B/H = AB/AC = 4/8.5
cosec A = H/P = 8.5/15
L.H.S. 1+ cot2 A = 1 + 16/56.25
72.25/56.25
= 289/225
R.H.S. cosec² A = H/P = (72.25/7.5)²
= (17/15)²
= 289/225
∴ L.H.S = R.H.S.
8. If sin C = 2/3, then let us write by calculating, the value of cos C x cosec C.
Solution: sin C = 2/3
sin C = P/H = AB/AC = 2/3
BC² = (AC)²- (AB)²
= (3)² – (2)²
= 9 – 4
= 5
∴ BC = √5
cos C x cosec C
= B/H x H/P
= √5/3 x 3/2
= √5/2
9. Let us write with reason whether the following statements are true or false
1. The value of tan A is always greater than 1.
Solution. The statement is false
if the perpendicular is greater than the base then tan A will be greater than 1, but if the base is greater than the perpendicular then tan A is less than 1.
2. The value of cot A is always less than 1.
Solution. The statement is false.
3. For an angle 8, it may be possible that sin 0 = 4/3
Solution. The statement is false.
As sinθ = perpendicular/hypotenuse
i.e., sin θ = 4/3 here, the perpendicular of a triangle can not be greater than the hypotenuse.
4. For an angle a, it may be possible that secα =
Solution. The statement is true.
As sec θ = hypotenuse/base
i.e., secθ= 12/5, the hypotenuse is always greater than the base.
Maths WBBSE Class 10 Solutions
5. For an angle ẞ(Beta), it may be possible that cosecẞ:
Solution. The statement is false.
As cosec θ = hypotenuse/perpendicular
i.e., cosec θ = 5/13, the hypotenuse is less than perpendicular.
6. For an angle 0, it may be possible that cos e = 3/5
Solution. The statement is true.
As cose = base/hypotenuse
i.e., cos e = 3/5′ here base is less than the hypotenuse.
10. I have understood, cosec 45° = 1/sin 45° = √2
= sec 45° = 1/cos 45°
= 1/ 1/√2 = √2
& cot 45° = 1/tan 45° = 1
I have understood, cosec 30° = 2,
sec 30° = 2/√3
and cot 30° = 1/tan 30°
=√3
Application 9. If the kite would be flown with a string of 120 m in length and the kite is at an angle of 30° with the horizontal line, then let us calculate the height of the kite from Rina’s position from the ground,
Solution:
Given
If the kite would be flown with a string of 120 m in length and the kite is at an angle of 30° with the horizontal line
AB is the height of the kite from the ground
& AC is the length of string = 120 m.
& angle of elevation (∠C) = 30°.
∴ sin30° = AB/AC or, 1/2 = AB/120
∴ AB = 120/2 = 60 m.
∴ The kite is 60 m above the ground.
Application 11. In a right-angled triangle ABC, ZB is a right angle. If AB = 5. cm and AC 10 cm, then let us determine the values of ∠BCA and ∠CAB.
Solution:
Given
In a right-angled triangle ABC, ZB is a right angle. If AB = 5. cm and AC 10 cm
In a right-angled triangle ABC, ∠B is a right angle,
AB 5 cm. and AC = 10 cm.
In a right-angled triangle, ABC, sin ∠BCA = AB/BC
= 5/10
= 1/2
= sin 30°
∴ ∠BCA = 30°
∴ ∠CAB = 90° – 30° = 60°
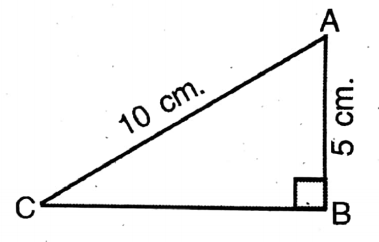
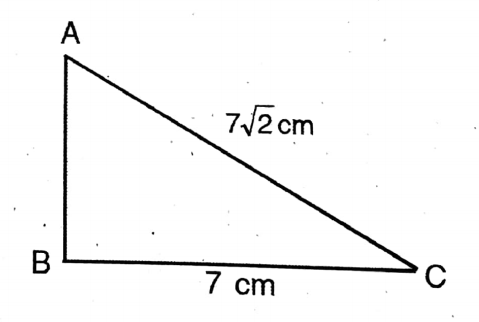
Application 12. In a right-angled triangle ABC, ∠B is a right angle. If AB = 7 cm and AC=7√2 cm, then let us write by calculating, the values of ∠BCA and ∠CAB.
Solution:
Given
In a right-angled triangle ABC, ∠B is a right angle. If AB = 7 cm and AC=7√2 cm
cos∠CAB = AB/AC
= 7 cm/7√2 cm
= 1/√2
= cos 45°
∴ ∠CAB = 45°
Application 14. Let us show that, tan²60° + 1 = sec²60°
Solution: L.H.S = tan² 60° + 1
=(√3)+1
=3+1
=4
=(2)²
= sec²60°
= R.H.S.
Application 17. Let us prove that, tan²60°-2sin60° = 3-cot30°
Solution: L.H.S. = tan²60 – 2sin²60
=(√3)-2. √3/2
= 3 – √3
R.H.S=3
cot30° = 3-√3.
∴ L.H.S = R.H.S.
