Maths WBBSE Class 10 Solutions Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.2
Question 1. In the window of our house, there is a ladder at an angle of 60° with the ground. If the ladder is 2√3 m long, then let us write by calculating the height of our window above the ground.
Solution: Let AB is the height of the window & AC is the ladder = 2√3 m.
∠ACB = 60°
∴ sin60° = AB/AC
√3/2 = AB/2√3
or, 2 AB=2√3.√3 = 6
∴ AB 6/2 = 3 m.
Read and Learn More WBBSE Solutions For Class 10 Maths
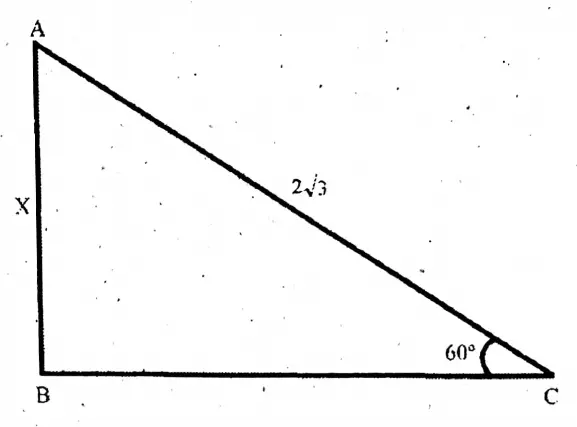
Question 2. ABC is a right-angled triangle with its B being 1 right angle. If AB = 8√3 cm and BC = 8 cm, then let us write by calculating, the values of ∠ACB and <BAC.
Solution: tan ∠ACB = AB/BC
= 8√3 cm / 8cm
= √3
= tan 60°
∴ ∠ACB = 60°
∴ ∠BAC 180°= (90° +60°)
= 180° – 150°
= 30°
Maths WBBSE Class 10 Solutions
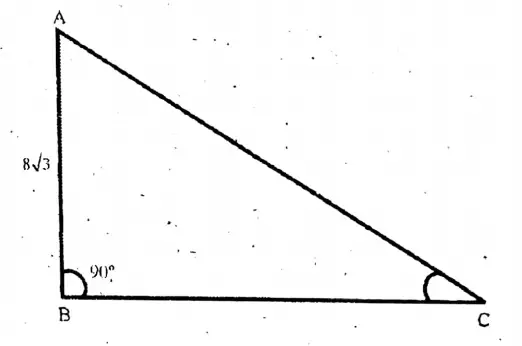
Question 3. In a right-angled triangle ABC, ∠B = 90°,∠A = 30°, and AC = 20 cm. Let us determine the lengths of the two sides BC and AB.
Solution: ∠A 30°, ∠B = 90°
∴ ∠C = 60°
sin60° = AB/AC
Or, √3/2 = AB/20
∴ AB = 20√3
= 10√3 cm.
Again, cos60° = BC/AC
1/2= BC/20
∴ BC = 20/2
= 10cm.
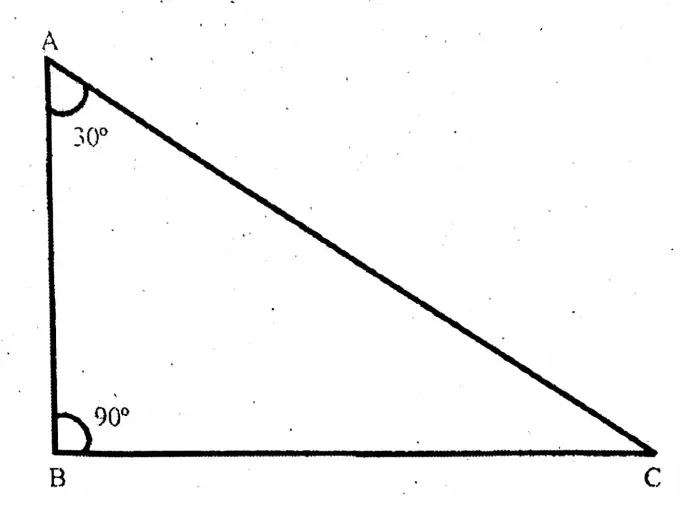
Question 4. In a right-angled triangle PQR, ZQ = 90°, ZR = 45°; if PR = 3√2, then let us find out the lengths of the two sides PQ and QR.
Solution: In ΔPQR, ∠Q= 90°, ∠R = 45°
∴ ∠P 90° – 45° = 45°
sin45° = PQ/PR
1/√2 = PQ/3√2
∴ PQ = 3√2/√2
= 3 units.
cos45° = QR/PR
1/√2 = QR/ 3√2
√2QR = 3√2
∴ QR = 3√2/√2
= 3 units.
Maths WBBSE Class 10 Solutions
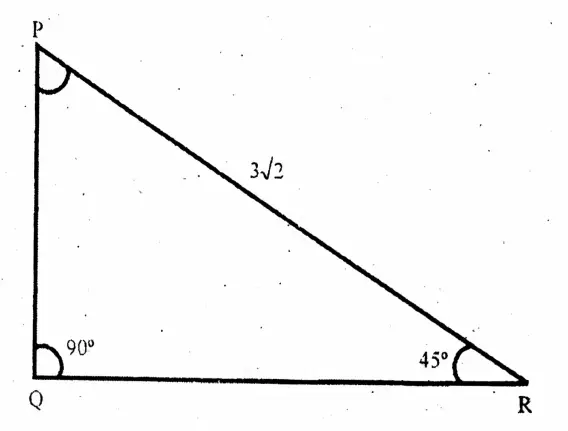
Question 5. Let us determine the values of
1. sin? 45° cosec² 60° + sec² 30°
Solution: sin² 45°- cosec² 60° + sec² 30°
= (1/√2)² – (2/√3)² + (2/√3)²
= 1/2 – 4/3 + 4/3
= 1/2
2. sec² 45°- cot² 45°- sin² 30° – sin² 60°
Solution: sec² 45°-cot² 45°- sin² 30° sin² 60°
= (√2)² -(1)² – (1/2)² – (√3/2)²
=2-1-1/4 -3/4
= 8-4-1-3 / 4
= 8-8/4
= 0/4
= 0
WBBSE Solutions Guide Class 10
3. 3tan² 45°- sin² 60° – 1/3 cot² 30° – 1/8 sec² 45°
Solution: 3tan² 45°- sin² 60° – 1/3 cot² 30° – 1/8 sec² 45°
= 3(1)²- (√3 /2)² – 1/8(√2)²
= 3×1 – 3/4 – 1/3 x 3 – 1/8 x 2
= 3 – 3/4 – 1 – 1/4
= 12-3-4-1 / 4
= 12-8 / 4
=4/4
= 1.
4. 4/3 cot² 30° + 3 sin² 60°-2cosec² 60°-
Solution: 4/3 cot² 30° + 3 sin² 60° – 2cosec² 60°- tan² 30°
= 4/3(√3)² + 3 (√3/2)² – 3/4(1/√3)
= 4/3 x 3 + 3/4 -2 4/3 x 3/4 x 1/3
= 4 + 9/4 – 8/3 – 1/4
= 48+27-32-3 / 12
= 75 – 35 / 12
= 40/12
= 10/3
= 3 1/3
WBBSE Solutions Guide Class 10
5. ⅓ cos 30°/ ½ sin45° + tan 60°/cos30°
Solution : ⅓ cos 30°/ ½ sin45° + tan 60°/cos30°
6. cot²30°-2cos² 60°- 3/4 sec² 45°-4sin² 30°
Solution: cot²30°-2cos² 60°- 3/4 sec² 45°-4sin² 30°
= (√3)² -2(1/2)² – 3/4 (√2)²- 4(1/2)²
=3-2 x 1/4 – 3/4 x 2-4 x 1/4
= 3- 1/2 – 3/2 – 1
= 6-1-3-2 / 2
= 6-6 / 2
= 0.
7. sec² 60°-cot² 30°- 2tan30°cosec60° / 1+tan²30°
Solution: sec² 60° cot² 30°- 2tan30°cosec60° / 1+tan²30°
8. tan60° – tan30° / 1+tan 60° tan 30° + cos60° cos30° + sin60°sin30°
Solution: tan60° – tan30° / 1+tan 60° tan 30° + cos60° cos30° + sin60°sin30°
WBBSE Solutions Guide Class 10
9. 1-sin² 30°/1+sin² 30° x cos²60+ cos² 30°/cos ec²90°-cot² 90° ÷ (sin 60° tan30°)
Solution : 1-sin² 30°/1+sin² 30° x cos²60+ cos² 30°/cosec²90°-cot² 90° ÷ (sin 60° tan30°)
= 3/4 x 2/3 x 1 x 2
= 1/2 x 2
= 1
Question 6.
1. sin² 45° + cos² 45° = 1
Solution: sin² 45° + cos² 45° = 1
L.H.S. sin²45+ cos²45 = (1/√2)² + (1/√2)²
= 1/2 + 1/2
= 1
2. cos60° = cos²30° – sin²30°
Solution: cos60° = cos²30° – sin²30°
L.H.S. = cos60° = 1/2
R.H.S = cos²30° – sin²30°
= (√3/2)² – (1/2)²
= 3/4 – 1/4
= 2/4
= 1/2
∴ L.H.S = R.H.S Proved.
3. 2 tan30°/1-tan²30° = √3
Solution: 2 tan30°/1-tan²30° = √3
Ganit Prakash Class 10 Solutions Pdf In English
= √3
∴ L.H.S = R.H.S Proved.
4.√(1+ cos30° / 1-cos30°) = sec 60° + tan 60°
Solution: √(1+ cos30° / 1-cos30°) = sec 60° + tan 60°
= sec60° + tan60°
= 2+ √3
∴ L.H.S = R.H.S Proved.
5. 2 tan² 30°/1-tan²30° + sec² 45°- cot² 45° = sec 60°
Solution : 2 tan² 30°/1-tan²30° + sec² 45°- cot² 45° = sec 60°
L.H.S. = 2 tan² 30°/1-tan²30° + sec² 45°- cot² 45°
R.H.S = sec 60° = 2
∴ L.H.S = R.H.S Proved.
Ganit Prakash Class 10 Solutions Pdf In English
6. tan² Π/4 sin Π/3 tanΠ/6 tan² Π/3 = 1 1/2
Solution: tan²Π/4 sin Π/3 tanΠ/6 tan² Π/3 = 1 1/2
L.H.S. = tan2 Π/4 sin Π/3 tanΠ/6 tan2 Π/3
= tan²45°sin60°tan30°tan260°
= (1)2. (√3/2) . 1/√3 . (√3)2
= 1/2 .3
= 3/2
= 1 1/2 = R.H.S.
.. L.H.S = R.H.S Proved.
7.sinΠ/3 tanΠ/6 + + sinΠ/2 cosΠ/3 = 2sin²Π/4
Solution: sinΠ/3 tanΠ/6 + + sinΠ/2 cosΠ/3 = 2sin²Π/4
L.H.S. sin = Π/3 tanΠ/6 + sinΠ/2– cosΠ/3
= sin60°tan30° + sin90°cos60°
= √3/2 . 1/√3 + 1 . 1/2
= 1/2 + 1/2
R.H.S= 2sin² = 2.
sin²45° = 2x (1/√2)²
= 2 x 1/2
= 1
∴ L.H.S = R.H.S Proved.
Ganit Prakash Class 10 Solutions Pdf In English
Question 7.
1. If x sin45° cos45° tan60° = tan² 45°- cos60°, then let us determine the value of x.
Solution: x sin45° cos45° tan60° = tan² 45° – cos60°
or, x . 1/√2 . 1/√2 .√3
= (1)² – 1/2
= x√3/2
= 1/2
or, √3x = 1
2. If x sin 60° cos² 30° = tan² 45° sec60° / cosec60° then let us determine the value of x.
Solution: x sin 60° cos² 30° = tan² 45° sec60° / cosec60°
3. If x²= sin²30° + 4cot² 45°- sec² 60°, then let us determine the value of x.
Solution: x² = sin²30° + 4cot² 45°- sec² 60°
or, x² = (1/2)² +4. (1)²- (1)²
or, x² = 1/4 + 4 – 4
x² = 1/4
x = 1/2
Ganit Prakash Class 10 Solutions Pdf In English
Question 8. If x tan 30° + y cot 60° = 0 and 2x – y tan 45° = 1, then let us write by calculating, the values of x and y.
Solution: x tan 30°+ y cot 60° = 0
or, x . 1/√3 + Y . 1/ √3 = 0
or, x/√3 + y/√3 = 0
or, or, x + y = 0——–(1)
Again 2x – y. 1 = 1
or, 2x – y = 1 ——-(2)
∴ x + y = 0
2x – y = 1
Adding 3x = 1
∴ X = 1/3
∴ Y = -X ∴ Y = – 1/3
Question 9. If A B 45°, then let us justify:
1. sin (A + B) = sin A cos B + cos A sin B
Solution: L.H.S= sin (A + B)
=sin(45° +45°)
= sin90°
= 0
R.H.S sinA cosB + cosA sinB
= sin45° cos45° + cos45° sin45°
= 1/√2 x 1/√2 x 1/√2 x 1/√2
= 1/2 + 1/2
= 1
∴ L.H.S = R.H.S
2. cos (A + B) = cos A cos B-sin A sin B
Solution: L.H.S= cos (A + B)
= cos(45° + 45°) = cos90° = 0
R.H.S. cosA cosB – sinA sinB
= cos45 cos45 – sinA sinB
= 1/√2 . 1/√2 – 1/√2 . 1/√2
= 1/2 – 1/2
= 0
∴ L.H.S = R.H.S
Ganit Prakash Class 10 Solutions Pdf In English
Question 10.
1. In an equilateral triangle ABC, BD is a median. Let us prove that, tan ∠ABD = cot <BAD.
Solution: L.H.S. tan ∠ABD = P/B
= AD/BD
R.H.S. cot <BAD = B/P
= AD/BD
∴ L.H.S. = R.H.S.
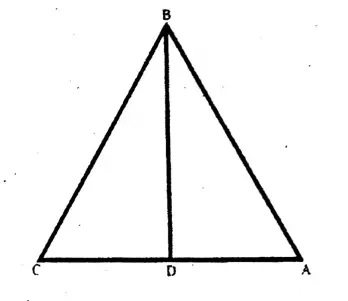
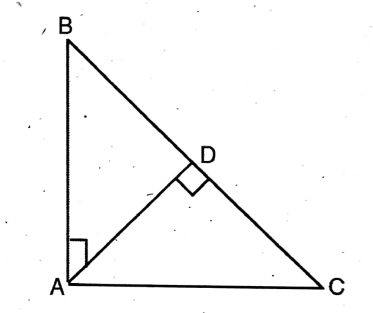
2. In an isosceles triangle ABC, AB = AC and <BAC 90°; the bisector of ∠BAC intersects the side BC at point D.
Solution: L.H.S = sec ∠ACD/sin <CAD
= AC/CD/CD/AC
= AC/CD x AC/CD
= AC²/CD²
R.H.S. cosec² ∠CAD
=(AC/CD)² = AC²/CD²
∴ L.H.S = R.H.S Proved.
11. Let us determine the value / values of 0(0°≤ 0≤ 90°), for which 2cos²θ-3cosθ +10 wil be true.
Solution: 2cos²θ-3cosθ + 1 = 0
or, 2cos²θ – 2cos θ – 1cosθ + 1 = 0
or, 2cosθ (cosθ-1) – 1 (cosθ-1)=0
Either cosθ1=0 ∴ cosθ = 1 = cos0°
∴ 0 = 0°
Or, 2cosθ – 1 = 0
∴ 2cosθ = 1
∴ cosθ = 1/2 = cos60°
∴ 0 = 60°
∴ Values of = 0° or 60°.
Maths WBBSE Class 10 Solutions
Application 23. For 0° ≤ 0 ≤ 90°, let us write with reason whether sin = √3/2 and cos = 1/3 are possible or not.
Solution: sin θ = √3/2, cos θ = 1/3
sin²θ + cos²θ = (√3/2)² + (1/3)²
= 3/4 + 1/9
= 27+4 / 36
= 31/36
∴ It is impossible as
we know sin² θ + cos² θ = 1
Application 26. I express cote and cosec e in terms of cos e.
Solution: We know, sin² θ+ cos² θ= 1
∴ sin²θ= 1 – cos²θ
or, sin θ = √1-cos²θ
∴ cos θ = cos θ/sin θ = cos θ/√1-cos²θ
Again, sin θ= √1-cos²θ ∴cosec θ = 1/sin θ
= 1/√1-cos²θ
Maths WBBSE Class 10 Solutions
Application 28. If tan θ = 3/4, then let us write by calculating, the value of (sinθ + cos θ)
Solution: sec²θ = 1 + tan²θ = 1 +(4/3)²
= 1 + 16/9
= 9+16 / 9
= 25/9
= (5/3)²
Secθ= 5/3 ∴ cos θ = 3/5
sinθ = √1-cos²θ
= √1- 9 /25
= √25-9 / 25
= √16/25
= 4/5
∴ sinθ + cos θ = 3/5 + 4/5
= 3+4 / 5
= 7/5
Application 34. If 5cote+cosec 0/5cot 0-cosec 0 = 7/3, then let us determine the value of cose.
Solution: 5cotθ+cosec θ/5cot θ-cosec θ = 7/3
= 35cotθ – 7cosecθ= 15cotθ + 3cosecθ
35cotθ – 15cotθ = 3cosecθ+7cosecθ
20cotθ = 10cosecθ
cot θ/cosecθ 10/20
cos θ/sinθ x sinθ = 1/2
∴ cosv =1/2
Application 36. From the two relations 2x= 3sine and 5y = 3cose, by eliminating, let us write the relation between x and y.
Solution: 3sinθ = 2x And 3cosθ = 5y
∴ sinθ=2x/3 ∴cosθ =5y/3
We know, sin² + cos² = 1
or, (2x/3)² + (5y/3)² = 1
or, 4x²/9 + 25y²/9 = 1
or, 4x²+ 25y² = 9.
Application 38. Let us eliminate from the two relations x = a sec e, y = b tan e.
Solution: a secθ = x And b tan θ = y
∴ secθ= x/a ∴ tanθ = y/b
We know, sec²θ-tan²θ = 1
or, (x/a)² – (y/b)² = 1 ∴ x²/a² – y²/b² = 1
Maths WBBSE Class 10 Solutions
Application 41. If cosθ + secθ = 2, then let us determine the value of (cos¹¹θ + sec¹¹θ) [Let me do it myself]
Solution: cosθ + secθ = 2 or, cos²+1=2cos
or, cose + 1/cos Ꮎ = 2
or, cos²0 – 2cose + 1 = 0 ∴(cose–1)²= 0
∴ cose – 1 = 0
sece= 1/cos 0
= 1/1
= 1
cose + sece
= (cose)¹¹+ (sece)¹¹
=(1)¹¹+ (1)¹¹
=1+1
=2
