WBBSE Solutions For Class 10 Maths Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3

WBBSE Class 10 Maths Solutions Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3

Question 1. If sinθ = then let us write the value of cosec/1+cotθ by determining it.

Solution : sinθ =4/5

∴ cosecθ =1/sinθ

=5/4

cot²θ = cosec²θ – 1 = (5/4)²-1

= 25/16-1

= 25-16 / 16

= 9/16

∴ cosθ= √9/16

= 3/4

Now, cosecθ / 1+cotθ = 5/4 / 1+3/4

= 5/4 x 4/7

= 5/7

Read and Learn More WBBSE Solutions For Class 10 Maths

Question 2. If tanθ = 3/4, then let us show that √(1-sinθ/1+sinθ) = 1/2

Solution: tanθ = 3/4

let AB =3K

& BC = 4K

∴ AC² = AB²+BC²

= (3K)²+(4K)² = 9K²+16K²

= 25K²

.. AC = √25K²

= 5K

∴ sinθ = AB/AC = 3K/5K = 3/5

Now L.H.S = \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sqrt{\frac{1-3 / 5}{1+3 / 5}}=\sqrt{\frac{\frac{5-3}{5}}{\frac{5+3}{5}}}=\sqrt{\frac{2}{8}}=\sqrt{\frac{1}{4}}\)

= 1/2 = R.H.S Proved

Question 3. If tanθ = 1, then let us determine the value of 8sinθ+5cosθ/sin³ θ-2cos³θ+7 cosθ

Solution: tanθ = 1

We know, \(\tan \theta=\frac{P}{B}=\frac{A B}{B C}\)

∴ \(\mathrm{AC}^2=\mathrm{AB}^2+\mathrm{BC}^2\)

= \((1 K)^2+(1 K)^2=K^2+K^2=2 K^2\)

∴ \(\mathrm{AC}^2=\mathrm{AB}^2+\mathrm{BC}^2\)

= \((1 K)^2+(1 K)^2=K^2+K^2=2 K^2\)

∴ \(A C=\sqrt{2 K^2}=K \sqrt{2}\)

∴ \(\sin \theta=\frac{P}{H}=\frac{A B}{A C}=\frac{1 K}{\sqrt{2} K}=\frac{1}{\sqrt{2}}\)

& \(\cos \theta=\frac{B}{H}=\frac{B C}{A C}=\frac{1 K}{\sqrt{2} K}=\frac{1}{\sqrt{2}}\)

Now, \(\frac{8 \sin \theta+5 \cos \theta}{\sin ^3 \theta-2 \cos ^3 \theta+7 \cos \theta}\)

= \(\frac{8 \times \frac{1}{\sqrt{2}}+5 \times \frac{1}{\sqrt{2}}}{\left(\frac{1}{\sqrt{2}}\right)^3-2\left(\frac{1}{\sqrt{2}}\right)^3+7 \cdot \frac{1}{\sqrt{2}}}=\frac{\frac{8}{\sqrt{2}}+\frac{5}{\sqrt{2}}}{\frac{1}{2 \sqrt{2}}-2 \frac{1}{2 \sqrt{2}}+\frac{7}{\sqrt{2}}}=\frac{\frac{13}{\sqrt{2}}}{\frac{1-2+14}{2 \sqrt{2}}}\)

= \(\frac{13 / \sqrt{2}}{13 / 2 \sqrt{2}}=\frac{13}{\sqrt{2}} \times \frac{2 \sqrt{2}}{13}=2\)

Question 2.

1. Let us express cosecθ and tanθ in terms of sine.

Solution: cosecθ= 1/sinθ

tanθ= sin/cos

= sinθ/√1-sin²θ

2. Let us write cosecθ and tanθ in terms of cosθ

Solution: cosecθ =1/sinθ = 1/√1-cos²θ

tanθ = sinθ/cosθ

= √1-cos²θ/cosθ

Question 3.

1. If secθ + tanθ = 2, then let us determine the value of (secθ– tanθ). 

Solution: We know, sec²θ tan²θ = 1

or, (secθ+tanθ) (secθ-tanθ) = 1

or, 2 x (secθ – tanθ) = 1

secθ – tanθ = 1/2

2. If cosecê – cote = √2-1, then let us write by calculating, the value of (cosecθ + cotθ).

Solution: We know, cosec²θ – cot²θ

or, (cosecθ+cotθ) (cosecθ- cotθ) = 1

or, (cosecθ+cotθ) (√2+1) = 1

∴ cosecθ+cotθ = 1/√2-1 

= (√2+1)/(√2-1)(√2+1) 

= (√2+1)/2-1 = √2+1 

3. If sinθ+cosθ = 1, then let us determine the value of sine x cosθ. 

Solution: sinθ + cosθ = 1

or, (sinθ+cosθ)² = 12

or, sin²θ+ cos²θ + 2sinθ x cosθ = 1

or, 1+2sinθ cosθ = 1          [as sin²θ + cos²θ = 1]

∴ 2sinθ cosθ = 0                => sinθ cosθ = 0.

West Bengal Board Class 10 Math Book Solution In English

4. If tanθ+cotθ = 1, then let us determine the value of (tanθ – cotθ). 

Solution: (tanθ-cotθ)²= (tanθ + cotθ) – 4. tanθ . cotθ

=(2)² – 4 x tanθ x 1/tan θ

=4-4=0.

∴tanθ – cotθ = 0

5. If sinθ – cosθ = 7/13 then let us determine the value of sinθ + cosθ.

Solution: (sinθ cosθ)² = (7/13)²

or, sin²θ+ cos²θ – 2sinθ cosθ = 49/169

or, 1 – 2sinθ cosθ = 49/169

or, 1-169 = 2sinθ cosθ

or, 169-49/169 = 2sinθ cosθ

or,  120/169 = 2sinθ cosθ

∴ (sine+cose)²= sin²θ+ cos²θ + 2sinθ cosθ

= 1 + 120/169

= 120+169/169

= 289/169

∴ sinθ+cosθ = √289/169

=17/13

6. If sinθcosθ = 1/2, then let us write by calculating, the value of (sinθ + cosθ).

Solution: (sinθ+cosθ)²= sin²θ+ cosθ²+2. sinθ. cosθ

= 1+2×1/2 =2.

∴ sinθ cosθ = √2.

7. If sin θ + cos θ/ sin θ-cos θ =7, then let us write by calculating, the value of tanθ.

Solution: sin θ + cos θ / sinθ-cos θ =7

or, \(\frac{\sin \theta+\cos \theta+\sin \theta-\cos \theta}{\sin \theta+\cos \theta-\sin \theta+\cos \theta}=\frac{7+1}{7-1}\)

or, \(\frac{2 \sin \theta}{2 \sin \theta}=\frac{8}{6}\)

or, \(\tan \theta=\frac{4}{3}\)

8.  If secθ+cosθ = 5/3 then let us write by calculating, the value of (secθ – cosθ).

Solution: (secθ – cosθ)²= (secθ+cosθ)² – 4. secθ. cosθ

= (5/3)²- 4 . sec x 1/secθ

= 25/9 – 4

= 25- 1 / 9

9. Let us determine the value of tan from the relation 5sin²0 + 4cos²0 = 9/2

Solution: 5sin²θ + 4cos²θ = 9/2

\(\text { 5. } \sin ^2 \theta+4\left(1-\sin ^2 \theta\right)=\frac{9}{2}\) \(5 \sin ^2 \theta-4 \sin ^2 \theta+4=\frac{9}{2}\) \(\sin ^2 \theta=\frac{9}{2}-4=\frac{9-8}{2}=\frac{1}{2}\)

∴ \(\cos ^2 \theta=1-\sin ^2 \theta=1-\frac{1}{2}=\frac{1}{2}\)

∴  \(\tan ^2 \theta=\frac{\sin ^2 \theta}{\cos ^2 \theta}=\frac{1 / 2}{1 / 2}=1\)

∴ \(\tan \theta=\sqrt{1}=1\)

10. If sec²θ + tan²θ =13/12 then let us write by calculating, the value of (sec10 – tan10).

Solution: sec⁴θ– tan⁴θ

= (secθ+tan²θ) (sec²θ – tan²θ)

= 13/12 x 1

= 13/12

Question 4.

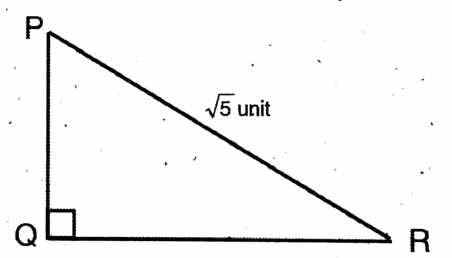
1. In ΔPQR, ∠Q is a right angle. If PR = √5 units and PQ – RQ = 1 unit, then let us determine the value of cos P – cos R.

Solution:

Given

In ΔPQR, ∠Q is a right angle. If PR = √5 units and PQ – RQ = 1 unit

cos P – cos R (given PQ – QR = 1)

= PQ/PR –  QR/PR 

= PQ-QR / PR 

= 1√5 unit

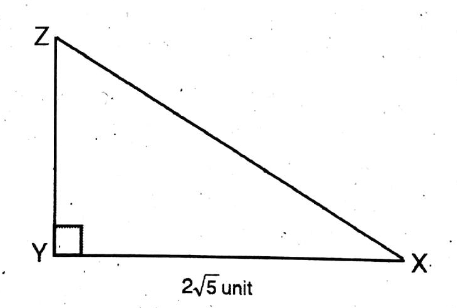
2. In ΔXYZ, Y is a right angle. If XY = 2√3 units and XZ – YZ = 2 units then let us determine the value of (sec X – tan X).

Solution: Given

In ΔXYZ, Y is a right angle. If XY = 2√3 units and XZ – YZ = 2 units

XY = 2√3 unit

& XZ – YZ = 2 units.

sec x – tan x

= \(\frac{X Z}{X Y}-\frac{Y Z}{X Y}\)

= \(\frac{X Z-Y Z}{X Y}=\frac{2}{2 \sqrt{3}}\)

∴ \(\sec X-\tan X=\frac{1}{\sqrt{3}}\)

Question 5. Let us eliminate ‘θ’ from the relations’

1. x = 2 sinθ, y = 3 cosθ

Solution: x = 2sinθ & y = 3coseθ

∴ sinθ = x/2          ∴ cosθ = y/3

We know, sin²θ + cos²θ = 1

∴ x²/4 + y2/9 = 1

2. 5x=3secθ, y = 3tanθ

Solution : 5x = 3 secθ;    &y = 3tanθ

∴ \(\sec \theta=\frac{5 x}{3}\)

∴ \(\tan \theta=\frac{y}{3}\)

We know, \(\sec ^2 \theta-\tan ^2 \theta=1\)

or, \(\left(\frac{5 x}{3}\right)^2-\left(\frac{y}{3}\right)^2=1\)

or, \(\frac{25 x^2}{9}-\frac{y^2}{9}=1\)

or, \(25 x^2-y^2=9\)

Question 6.

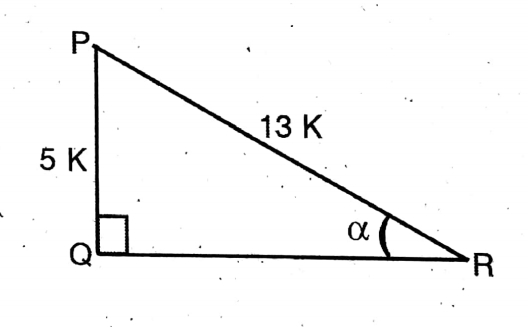
1. If sinα = 5/13 then let us show that, tanα+ secα = 1.5.

Solution: sinα = 5/13

Let PQ = 5k

PR = 13k

∴ QR = \(\sqrt{P R^2-P Q^2}\)

= \(\sqrt{(13 K)^2-(5 K)^2}\)

= \(\sqrt{169 K^2-25 K^2}=\sqrt{144 K^2}\)

∴ QR = 12k

∴ \(\tan \alpha+\sec \alpha=\frac{P}{B}+\frac{H}{B}=\frac{5 K}{12 K}+\frac{13 K}{12 K}=\frac{18 K}{12 K}=\frac{3}{2}=1.5\) Proved.

2. If tanA = n/m then let us determine the values of both sinA and secA.

Solution: tanA = n/m

or, \(\frac{\sin A}{\cos A}=\frac{n}{m}\)

⇒ \(\frac{\sin A}{\sqrt{1-\sin ^2 A}}=\frac{n}{m}\)

or, \(\frac{\sin ^2 A}{1-\sin ^2 A}=\frac{n^2}{m^2}\)

or, \(\frac{1-\sin ^2 A}{\sin ^2 A}=\frac{m^2}{n^2}\)

or, \(\frac{1}{\sin ^2 A}-\frac{\sin ^2 A}{\sin ^2 A}=\frac{m^2}{n^2}\)

or, \(\frac{1}{\sin ^2 A}-1=\frac{m^2}{n^2}\)

or, \(\frac{1}{\sin ^2 A}=\frac{m^2}{n^2}+1\)

or, \(\frac{1}{\sin ^2 A}=\frac{m^2+n^2}{n^2}\)

or, \(\sin ^2 A=\frac{n^2}{m^2+n^2}\)

∴ \(\sin A=\frac{n}{\sqrt{m^2+n^2}}\)

Again, \(\sec ^2 A-\tan ^2 A=1\)

or, \(\sec ^2 \mathrm{~A}=1+\tan ^{26} \mathrm{~A}\)

= \(1+\frac{n^2}{m^2}\)

= \(\frac{m^2+n^2}{m^2}\)

∴ \(\sec A=\sqrt{\frac{m^2+n^2}{m^2}}\)

3. If sec = x/√x² + y² then let us show that, x sinθ = y cosθ.

Solution:

⇒ \(\sin \theta=\sqrt{1-\cos ^2 \theta}=\sqrt{1-\left(\frac{x}{\sqrt{x^2+y^2}}\right)^2}\)

⇒ \(\sin \theta=\sqrt{1-\frac{x^2}{x^2+y^2}}=\sqrt{\frac{x^2+y^2-x^2}{x^2+y^2}}=\sqrt{\frac{y^2}{x^2+y^2}}=\frac{y}{\sqrt{x^2+y^2}}\)

∴ L.H.S. = x sinθ = \(x \cdot \frac{y}{\sqrt{x^2+y^2}}=\frac{x y}{\sqrt{x^2+y^2}}\)

R.H.S. = y cosθ = \(y \cdot \frac{x}{\sqrt{x^2+y^2}}=\frac{x y}{\sqrt{x^2+y^2}}\)

∴ L.H.S. = R.H.S.  Proved.

4. If sinα = a²-b² / a²+b² then let us show that, cotα = 2ab/a²-b²

Solution: sinα = a²-b² / a²+b²

∴ \(\cos ^2 \alpha=1-\sin ^2 \alpha=1-\frac{\left(a^2-b^2\right)}{\left(a^2+b^2\right)}=\frac{\left(a^2+b^2\right)-\left(a^2-b^2\right)}{\left(a^2+b^2\right)^2}\)

= \(\frac{\left(a^4+b^4+2 a^2 b^2\right)-\left(a^4+b^4-2 a^2 b^2\right)}{\left(a^2+b^2\right)^2}=\frac{4 a^2 b^2}{\left(a^2+b^2\right)^2}\)

∴ \(\cos \alpha=\frac{2 a b}{a^2+b^2}\)

⇒ \(\cot =\frac{\cos \alpha}{\sin \alpha}=\frac{2 a b /\left(a^2+b^2\right)}{\left(a^2-b^2\right) /\left(a^2+b^2\right)}\)

= \(\frac{2 a b}{\left(a^2+b^2\right)} \times \frac{\left(a^2+b^2\right)}{\left(a^2-b^2\right)}\)

∴ \(\cos \alpha=\frac{2 a b}{a^2-b^2}\) Proved.

5. If sinθ / x = cosθ / y then let us show that sinθ = x-y/√x² + y²·

Solution: sinθ / x = cos θ/ y = K(let)

∴ sinθ = xK & cosθ = yK

We know, \(\sin ^2 \theta+\cos ^2 \theta=1\)

or, \(\mathrm{x}^2 \mathrm{~K}^2+\mathrm{y}^2 \mathrm{~K}^2=1\)

or, \(\mathrm{K}^2\left(\mathrm{x}^2+\mathrm{y}^2\right)=1\)

∴ \(K^2=\frac{1}{x^2+y^2}\)

∴ \(K=\frac{1}{\sqrt{x^2+y^2}}\)

Now, sinθ – cosθ = xK – yK

= \(x \frac{1}{\sqrt{x^2+y^2}}-y \cdot \frac{1}{\sqrt{x^2+y^2}}\)

∴ \(\sin \theta-\cos \theta=\frac{x-y}{\sqrt{x^2+y^2}}\)  Proved.

6. If (1 + 4x²) cosA = 4x, then let us show that cosecA + cotA = 1+2x/1-2x

Solution: (1+ 4x²)cosA = 4x

∴ \(\cos A=\frac{4 x}{1+4 x^2}\)

⇒ \(\sin ^2 A=1-\cos ^2 A=1-\left(\frac{4 x}{1+4 x^2}\right)^2=\frac{\left(1+4 x^2\right)^2-16 x^2}{\left(1+4 x^2\right)^2}\)

= \(\frac{1+16 x^4+8 x^2-16 x^2}{\left(1+4 x^2\right)^2}=\frac{1+16 x^4-8 x^2}{\left(1+4 x^2\right)^2}=\frac{\left(1-4 x^2\right)^2}{\left(1+4 x^2\right)^2}\)

∴ \(\sin A=\frac{1-4 x^2}{1+4 x^2}\)

∴ \({cosec} A=\frac{1+4 x^2}{1-4 x^2}\)

⇒ \(\cot A=\frac{\cos A}{\sin A}=\frac{4 x / 1+4 x^2}{\left(1-4 x^2\right) / 1+4 x^2}=\frac{4 x}{1-4 x^2}\)

⇒ \({cosec} A+\cot A=\frac{1+4 x^2}{1-4 x^2}+\frac{4 x}{1-4 x^2}\)

= \(\frac{1+4 x^2+4 x}{1-4 x^2}=\frac{(1+2 x)^2}{(1+2 x)(1-2 x)}\)

∴ \({cosec} A+\cot A=\frac{1+2 x}{1-2 x}\)

Proved.

7. If x = a sine and y = b tanθ, then let us prove that a²/x²- b²/y² = 1

Solution: x = a sine & y = b tane

or, \(\sin \theta=\frac{x}{a}\)      ∴ \(\tan \theta=\frac{\mathrm{y}}{\mathrm{b}}\)

or, \({cosec} \theta=\frac{a}{x}\)   ∴ \(\cot \theta=\frac{b}{y}\)

We know, \({cosec}^2 \theta-\cot ^2 \theta=1\)

or, \(\frac{a^2}{x^2}-\frac{b^2}{y^2}=1\) Proved.

8. If sinθ + sin² = 1, then let us prove that cos²θ+ cos²θ = 1. 

Solution: sinθ + sin²θ = 1

∴ sinθ = 1 – sin²θ = cos²θ

∴ sin²θ = cos1θ

∴ cos²θ+ cos θ sine + sin²θ = 1 Proved

West Bengal Board Class 10 Math Book Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 Multiple Choice Question

1. If 3x = cosecα and 3/x = cot α ,then the value of 3(x² – 1/x²) is

1. 1/27
2. 1/81
3. 1/3
4. 1/9

Solution:  cosecα = 3x  & cot = 3/x

⇒ \({cosec}^2 \alpha-\cot ^2 \alpha=1\)

⇒ \((3 x)^2-\left(\frac{3}{x}\right)^2=1\)

or, \(9 x^2-\frac{9}{x^2}=1\)

or, \(3\left(3 x^2-\frac{3}{x^2}\right)=1\)

∴ 3x² – 3/x²

= 1/3

Answer: 3. 1/3

2. If 2x = sec A and 2/x = tan A, then the value of 2(x² – 1/x²)is

1. 1/2
2. 1/4
3. 1/8
4. 1/16

Solution: sec²A – tan²A= 1

or, \((2 x)^2-\left(\frac{2}{x}\right)^2=1\)

or, \(4 x^2-\frac{4}{x^2}=1\)

or, \(4\left(x^2-\frac{1}{x^2}\right)^2=1\)

⇒ \(2\left(x^2-\frac{1}{x^2}\right)^2=\frac{1}{2}\)

Answer: 1. 1/2

3. If tan∝ + cot ∝ = 2, then the value of (tan¹³∝ + cot¹³∝) is

1. 1
2. 0
3. 2
4. None

Solution: tan∝ + cot∝ = 2

or, \(\tan \alpha+\frac{1}{\tan \alpha}=2\)

⇒ \(\frac{\tan ^2 \alpha+1}{\tan \alpha}=2\)

or, \(\tan ^2 \alpha+1=2 \tan \alpha\)

or, \(\tan ^2 \alpha-2 \tan \alpha+1=0\)

⇒ \((\tan \alpha-1)^2=0\)

∴ tanα = 1 & cotα = 1

∴ \(\tan ^{13} \alpha+\cot ^{13} \alpha\)

= \((\tan \alpha)^{13}+(\cot \alpha)^{13}\)

= 1 + 1 = 2

Answer: 3. 2

4. If sin 0 – cos 0 = 0 (0º ≤θ≤ 90º) and sec θ + cosec θ = x, then the value of x is

1. 1
2. 2
3. √2
4. 2√2

Solution: sinθ- cosθ = 0

sinθ = cosθ

= sinθ (90 – θ)

∴ θ = 90° – θ

∴ 2 = 90°

∴ θ = 45°

secθ- cosecθ = x

or, sec45° + cosec45° = x

or, √2 + √2 = x

∴ 2√2 = x

∴ x = 2√2

Answer: 4. 2√2

5. If 2cos³θ = 1, then the value of θ is

1. 10º
2. 15º
3. 20º
4. 30º

Solution: 2cos³θ = 1

∴ cos3θ = 1/2 = cos60º

∴ 3θ = 60º           .. θ= 60º /2 = 20º

Answer: 3. 20º

West Bengal Board Class 10 Math Book Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 True Or False

1. If 0°< a < 90°, then the least value of (sec²α + cos²α) is 2.

Answer: True

2. The value of (cos0° x cos1° x cos2° x cos3° x…………..cos90°) is 1.

Answer: False

Class 10 WBBSE Math Solution In English Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 Fill In The Blanks

1. The value of (4/sec²θ+ 1/1+ cot²θ +3sin²θ) is————-

Solution: 4/sec² θ + 1/1+ cot²θ +3sin²θ

= 4cos²θ + sin²θ + 3sin²θ

= 4(cos²θ + sin²θ)

= 4 x 1

= 4

2. If sin (θ-30°) = 1/2 then the value of cos e is————

Solution: sin(θ – 30°) = 1/2 = sin30°

θ – 30° = 30°

θ = 30° + 30°              ∴ θ =- 60°

∴ cos θ= cos 60° = 1/2

3. If cos²θ – sin²θ = 1/2 , then the value of Cos⁴θ- sin⁴θ is ———

Solution: Cos⁴θ- sin⁴θ

(cos²θ)² – (sin²θ)²

= (cos²θ + sin²θ)(cos²θ – sin²θ)

= 1 x 1/2

= 1/2

Chapter 23 Trigonometric Ratios And Trigonometric Identities Exercise 23.3 Short Answers

1. If r cosθ = 2√3, r sinθ = 2, and 0º <θ <90º, then let us determine the values of both r and θ

Solution:

If r cosθ = 2√3, r sinθ = 2, and 0º <θ <90º

r cosθ = 2√3, r sinθ = 2

⇒ \(\frac{r \sin \theta}{r \cos \theta}=\frac{2}{2 \sqrt{3}}  or, \tan \theta=\frac{1}{\sqrt{3}}=\tan 30^{\circ}\)

∴ θ = 30°

Again, \(r^2 \cos ^2 \theta+r^2 \sin ^2 \theta=(2 \sqrt{3})^2+2^2\)

Or, \(r^2\left(\cos ^2 \theta+\sin ^2 \theta\right)=12+4=16\)

Or, \(r^2 \times 1=16\)

Or, \(x=\sqrt{16} \pm 4\)

2. If sinA + sinB = 2 where 0° SA≤ 90° and 0° B≤ 90°, then let us find out the value of (cosA+ cosB).

Solution.

If sinA + sinB = 2 where 0° SA≤ 90° and 0° B≤ 90°,

sinA + sinB = 2 

Greatest value of sinA          ∴ sin A = sin90°      ∴ A= 90°

Greatest value of sinB         ∴  sin B = sin90°        ∴ B = 90°

cosA + cosB = cos90° + cos90° = 0 + 0 = 0

3. If 0°<θ< 90°, then let us calculate the least value of (9tan²θ + 4cot2θ).

Solution. 9tan²θ+4cot²θ = (3tanθ)² + (2cot²θ)²

= (3tanθ2-cotθ)²-2. 3tanθ. 2cotθ

= (3tanθ-2cotθ)²-12 tanθ x 1/tanθ

∴ Least value of (9tan²θ+ 4cot²θ) is 12.

4. Let us calculate the value of ( Sin⁶+cos⁶+ 3sin²α cos²α).

Solution:  Sin⁶∝+cos⁶∝+3sin²α cos²α.

= (sin²α)³ + (cos²α)³ + 3. sin²a. cos²α(sin²α + cos²α)

= (sin²α + cos²α)³ = (1)³

= 1.

5. If cosec2θ = 2cote and 0° <0< 90°, then let us determine the value of 0.

Solution.

If cosec2θ = 2cote and 0° <0< 90°

cosec²θ = 2cote

or, 1+ cot²θ – 2cotθ = 0

or, (1 – cote)² = 0

1-cotθ=0               ∴ cotθ1 = cot45°

∴ 0 = 45°