Class 10 WBBSE Math Solution In English Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1
Application: 1. We understand that ZBCA and CAB are complementary [complementary/supplementary] to each other.
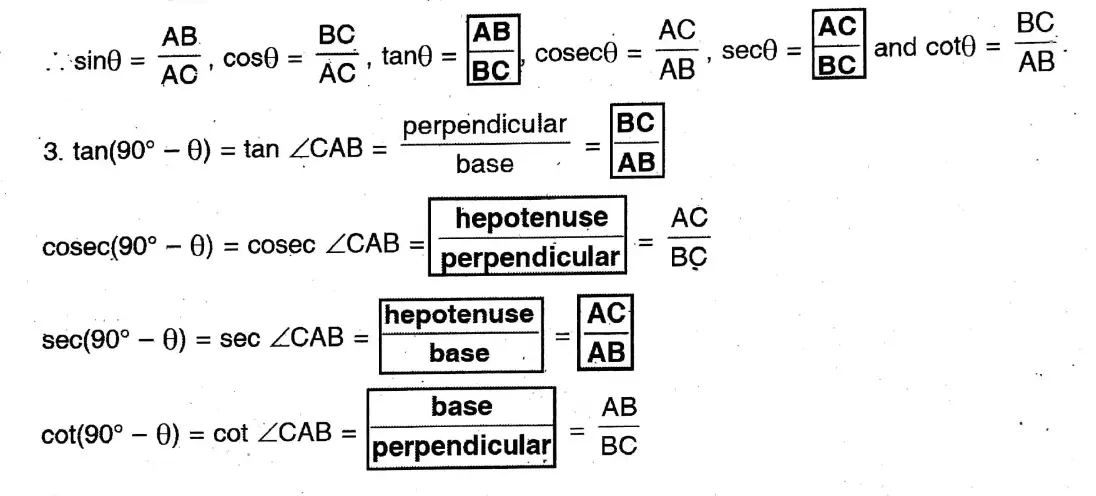
Read and Learn More WBBSE Solutions For Class 10 Maths
Application 2. Let us find the value of sec 90°/cosec41°
Solution: sec 49°/cosec41°
= sec 49°/cos ec(90° 49°)
= sec 49°/sec 49°
= 1
Application 3. Let us show that sin43° cos47° + cos43° sin47° = 1
Solution: sin43° cos47° + cos43° sin47°
=sin(90° 47°) cos47° + cos(90° 47°) sin47°
= cos47° cos47° + sin47° sin47°
= cos247° + sin247°
= 1
∴ L.H.S. = R.H.S. Proved.
Class 10 WBBSE Math Solution In English
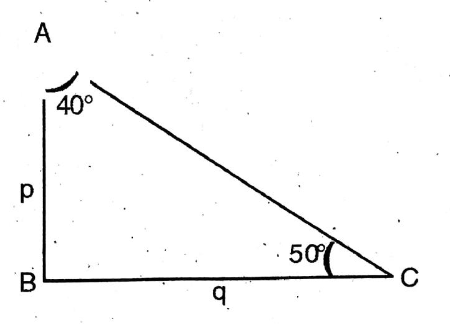
Application 13. If tan50° = P/q let us find the value of cos40°.
Solution: tan50° = p/q
AC² = AB² + BC²
= p² + q²
∴ AC = √ p² + q²
cos 40º = cos BAC = AB/AC = P/√ p² + q²
Question 1.
1. sin 38º/cos 52º
Solution: sin 38º/cos 52º
= sin38º/cos(30 – 38)º
= sin38º/sin38
= 1
2. cosec 79º/sec11º
Solution: cosec 79º/sec11º
= cosec 79º/sec(90º-79º)
= cosec 79º/cosec 79º
= 1
3. tan27º/cot63º
Solution: tan27º/cot63º
= tan(90º-63º)/cot63º
= cot63º/cot63º
= 1
Question 2.
1. sin66º – cos24º = 0
Solution: L.H.S = sin66º – cos24º
= sin(90º – 24º)
= cos 24º – cos 24º
= 0
= R.H.S
2. cos²57º + cos²33º = 1
Solution: cos²57º + cos²33º
= cos²(90º – 30º) + cos²33º
= sin²33º + cos²33º
= 1
= R.H.S
3. cos²75º-sin²12º = 0
Solution: L.H.S = cos²75º-sin²12º
= cos²(90º-15º) – sin²15º
= sin²15º – sin²15º
= 1
= R.H.S
4. cosec²48º – tan²42º = 1
Solution: L.H.S = cosec²48º – tan²42º
= cosec²48º – tan²(90º-48º)
= cosec²48º – cot²48º
= 1
= R.H.S
Class 10 WBBSE Math Solution In English
5. sec 70ºsin20º + cos20º cosec70º = 2
Solution: L.H.S = sec 70ºsin20º + cos20º cosec70º
= sec(90º – 20º) sin20º + cos20º. cosec(90º-20º)
= cosec20º . sin20º + cos20º x 1/cos20º
= 1+1
= 2
= R.H.S
Question 3. If two angles a and ẞ are complementary angles, let us show that:
1. sin’α + sin2ß = 1
Solution: L.H.S. = sin2α + sin2ß
= sin2(90-B) + sin2ß [As α + B = 90°]
=cos2B+ sin2B
= 1
= R.H.S.
2. cotẞ + cosẞ= cosẞ/cosα(1 + sinẞ)
Solution: R.H.S = cosẞ/cosα(1 + sinẞ)
3. secα/cosα – cot²β =1
Solution: L.H.S = secα/cosα – cot²β
= sec²α – cot²α(90º-α)
= sec²α – tan²α
= 1
= R.H.S
Class 10 WBBSE Math Solution In English
4. If sin 17° = x/y, let us show that sec17° – sin73° = x²/y√y²-x²
Solution: sin17º = x/y
WBBSE Solutions Guide Class 10
5. Let us show that sec²12° – 1/tan278°
Solution: L.H.S. = sec²12°
6. ∠A + ∠B = 90°, let us know that 1+tanA/tanB = sec²A
Solution: ∠A + ∠B = 90°
7. Let us show that cosec²22°cot²68° = sin²22°+sin²68°+cot²68°
Solution: L.H.S = cosec²22°cot²68°
8. If ∠P + ∠Q = 90º, let us show that, √sinP/cosQ – sinPcosQ = cosP
Solution: L.H.S = √sinP/cosQ – sinPcosQ P+Q = 90º , Q =90º-P
WBBSE Solutions Guide Class 10
9. Let us prove that cot12ºcot38ºcot52ºcot78ºcot60º = 1/√3
Solution: L.H.S = cot12ºcot38ºcot52ºcot78ºcot60º
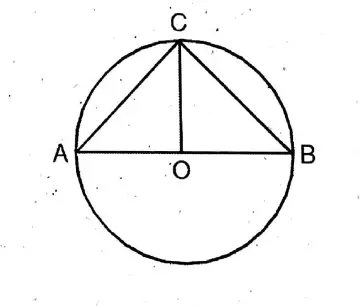
Question 10. AOB is a diameter of a circle with center O and C is any point on the circle, joining A, C; B, C; O, C, let us show that ZACB = semicircle angle = 90°
1. tan ∠ABC = cot ∠ACO
Solution: L.H.S. = tan ∠ABC
= tan(90° ∠ACO)
= cot∠ACO
= R.H.S [As OB = OC]
2. sin² ∠BCO + sin² ∠ACO = 1
Solution: L.H.S= sin² ∠BCO + sin² ∠ACO
= sin²(90° -∠ACO) + sin² ∠ACO
= cos²∠ACO + sin² ∠ACO
= 1. R.H.S.
3. cosec2 CAB – 1 = tan2 ZABC
Solution: L.H.S. cosec²∠CAB-1
= cosec²(90° – ∠ABC) – 1
= sec² ∠ABC – 1
= tan² ∠ABC
= R.H.S.
WBBSE Solutions Guide Class 10
Question 11. ABCD is a rectangular figure joining A, and C let us prove that:
1. tan ∠ACD = cot ∠ACB
Solution: tan ∠ACD tan(90° – ∠ACB)
= cot∠ACB= R.H.S
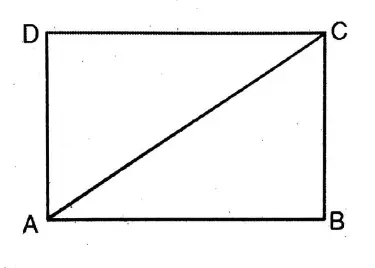
2. tan²∠CAD + 1 = 1/sin²∠BAC
Solution: tan²∠CAD + 11
= tan²(90° – <BAC) + 1
= cot²∠BAC +1
= cosec² ∠BAC
=1/sin²∠BAC
= R.H.S.
WBBSE Solutions Guide Class 10 Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 Multiple Choice Question
Question 1. The value of (sin43° cos47° + cos43° sin47°) is
1. 0
2. 1
3. sin4°
4. cos4°
Solution: sin43° cos47° + cos43° sin47°
= cos47°. cos47° + sin47°. sin47°
= cos247° + sin247°
= 1
Answer. 2. 1
Question 2. The value of tan35°/cot55° + cot78°/tan12°
1. 0
2. 1
3. 2
4. None of this
Solution : tan35°/cot55° + cot78°/tan12°
= tan 35°/cot(90-35°) + cot 78°/ tan(90°-78°)
= tan 35° /tan 35° + cot 78°/cot 78°
=1+1
=2
Answer. 3. 2
Question 3. The value of {cos(40° +8) sin(50° – 0)} is
1. 2cosθ
2. 7sinθ
3. 0
4. 1
Solution: cos(40 + θ) – sin(50 – θ)
= cos(40+θ) cos(90 (50-θ)}
= cos(40+θ) cos(40 + θ)
= 0
Answer: 3. 0
Maths WBBSE Class 10 Solutions
Question 4. ABC is a triangle. sin(B+C/2)
1. sin A/2
2. Cos A/2
3. sin A
4. cosA
Solution: A/2 + B/2 + C/2 = 90º
Question 5. iF A+B = 90º and tan A = 3/4, value of cot B is.
1. 3/4
2. 4/3
3. 3/5
4. 4/5
Solution: cot B = cot(90º – A) = tanA = 3/4
Answer: 1. 3/4
Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 True Or False
Question: 1. The values cos54° and sin36° are equal.
True
Question 2. The simplified value of (sin12° – cos78°) is 1
False
Maths WBBSE Class 10 Solutions Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 Fill In The Blanks
1. The value of (tan15° x tan45° x tan60° x tan78°) is √3.
2. The value of (sin12° x cos18° x sec78° x cosec72°) is 1.
3. If A and B are complementary to each other, sin A = cos B.
Maths WBBSE Class 10 Solutions Chapter 24 Trigonometric Ratios Of Complementary Angle Exercise 24.1 Short Answer
Question 1. If sin 10θ cos8θand 100 is a positive acute angle, let us find the value of tan 9θ.
Solution. sin10θ = cos8θ
or, sin10θ = sin(90° – 8θ)
or, 10θ = 90°-8θ
18θ = 90° θ = 90/18 = 5°
= tan9θ
= tan(9 x 5°)
= tan45°
= 1
Question 2. If tan4θ x tan60 = 1 and 60 is a positive acute angle, let us find the value of θ.
Solution. tan4θ x tan6θ = 1
or, tan4θ = 1/tan 6θ
cot6θ = tan(9θ-6θ)
∴ 4θ = 90-6θ
or, 10θ = 90 ∴ 0 = 90/10
= 9°
Question 3. Let us find the value of 2sin²63°+1+2sin²27°/ 3cos²17° -2+3cos² 73°
Solution: 2sin²63°+1+2sin²27°/ 3cos²17° -2+3cos² 73°
Question 4. Let us find the value of (tan1° x tan2° x tan3°———-tan89°).
Solution: tan1º x tan89º x tan2º x tan88º
= 1 x 1 x 1
= 1
Question 5. If sec5A = cosec (A + 36°) and 5A is a positive acute angle, let us find the value of A.
Solution. sec5A = cosec(A + 36)
= cosec(90° 5A) = cosec(A + 36°)
or, 90° – 5A = A + 36°
or, 90° – 36° 5A + A
or, 6A = 54°
A = 9°.
