Maths WBBSE Class 10 Solutions Chapter 25 Application Of Trigonometric Ratios Heights & Distances Exercise 25.1
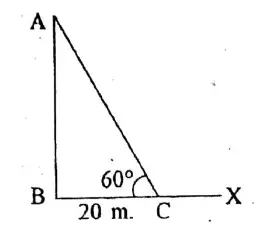
Application 1. If the angle of elevation at the top of the coconut tree is 60° with respect to a point which is 20 metres away in the horizontal plane from the foot of the coconut tree, let us write by calculating the height of the coconut tree.
Solution:
Given
If the angle of elevation at the top of the coconut tree is 60° with respect to a point which is 20 metres away in the horizontal plane from the foot of the coconut tree,
tan60° = AB/BC
or, √3 = AB/20
∴AB = 20 √3 m.

Read and Learn More WBBSE Solutions For Class 10 Maths
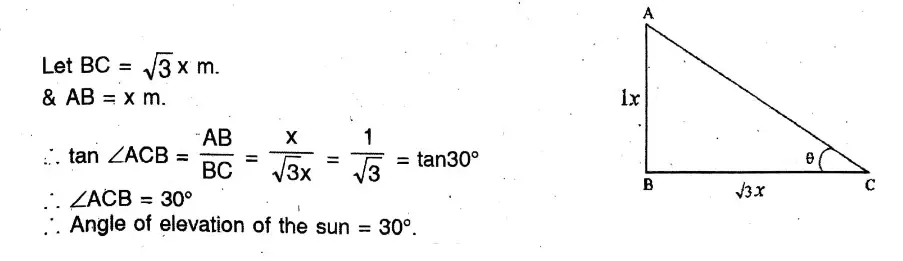
Application 2. Let us find what will be the angle of elevation of the sun when the length of the shadow of a stick of 20 metres will be 12√3 metres.
Solution: tanC = AB/BC
= 20/ 20√3
= 1/√3
= tan 30°
∴ ∠C = 30°
Application 3. From a point at the top of a building of 60 metres height, it is observed that the angles of depression of the top and foot of the tower are 30° and 60° respectively. Let us write by calculating the height of the tower.
Solution:
In ΔABC, from a point at the top of a building of 60 metres height, it is observed that the angles of depression of the top and foot of the tower are 30° and 60° respectively.rom a point at the top of a building of 60 metres height, it is observed that the angles of depression of the top and foot of the tower are 30° and 60° respectively.
tan60° = \(\frac{AB}{BC}\)
∴ \(\sqrt{3}=\frac{60}{B C}\)
∴ \(B C=\frac{60}{\sqrt{3}}=\frac{60 \sqrt{3}}{3}\)
= 20 √3 m.
∴ DE = 20 √3
In △ADE, tan30° = \(\frac{AD}{DE}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{A D}{20 \sqrt{3}}\)
∴ √3 AD = 20√3
∴BC= DB = AB – AD
=60-20 = 40 m.
∴ Height of the building = 40 m
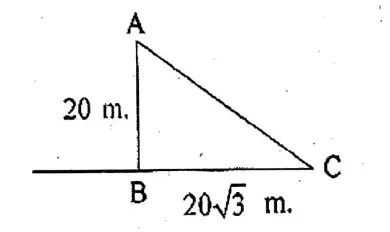
Question 4. If the angle of elevation of the top of a coconut tree from a point on the ground is 60° and the point is 20 metres away from the foot of the tree, let us find the height of the tree.
Solution:
If the angle of elevation of the top of a coconut tree from a point on the ground is 60° and the point is 20 metres away from the foot of the tree
AB = coconut tree
In ΔABC,
tan C = \(\frac{AB}{BC}\)
or, tan60° = \(\frac{AB}{20 m}\)
or, √3 = \(\frac{AB}{20 m}\)
∴ AB = 20 √3 m
∴ Height of the tree = 20 √3 m
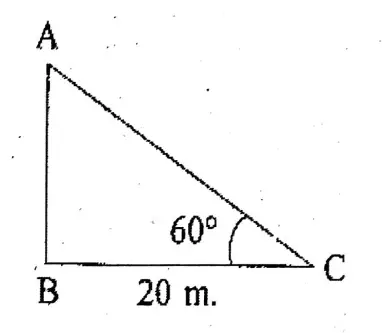
Question 5. The length of the shadow of a tower is 9 metres when the sun’s angle of elevation is 30°. Let us write by calculating the height of the tower.
Solution:
The length of the shadow of a tower is 9 metres when the sun’s angle of elevation is 30°.
AB = Tower
BC = Length of shadow = 9 m
In ΔABC,
tan C = \(\frac{AB}{BC}\)
or, tan30° = \(\frac{AB}{9m}\)
or, \(\frac{1}{\sqrt{3}}=\frac{A B}{9 m}\)
∴ \(A B=\frac{9}{\sqrt{3}}=\frac{9 \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}}=\frac{9 \sqrt{3}}{3}=3 \sqrt{3} \mathrm{~m}\)
∴ Height of the tower = 3√3 m.
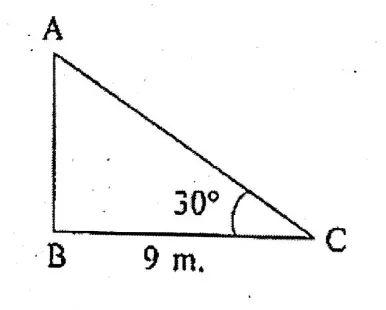
Question 6. A kite is flying with a thread of 150 metres long from a field. If the thread of the kite makes an angle of 60° with the horizontal line, let us write by calculating the height of the kite from the ground.
Solution:
A kite is flying with a thread of 150 metres long from a field. If the thread of the kite makes an angle of 60° with the horizontal line,
Here, let the height of Kite = AB
length of the thread = AC = 150m.
In ABC
sinC = \(\frac{AB}{AC}\)
or, \(\sin 60^{\circ}=\frac{A B}{A C}\)
or, \(\frac{\sqrt{3}}{2}=\frac{A B}{150}\)
or, 2 x AB = 150√3
∴ \(A B=\frac{150 \sqrt{3}}{2}=75 \sqrt{3} \mathrm{~m}\)
∴ Height of the Kite = 75√3 m.
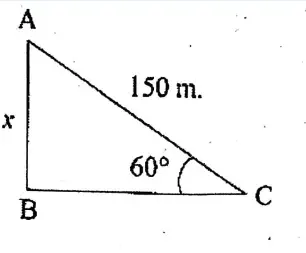
Question 7. A palm tree stands on the bank of a river. A post is fixed in the earth on the other bank just opposite the palm tree. On moving 7 √3 metres from the post along the bank, it is found that the tree makes an angle of 60° at that point with respect to this bank. Let us find the width of the river.
Solution:
A palm tree stands on the bank of a river. A post is fixed in the earth on the other bank just opposite the palm tree. On moving 7 √3 metres from the post along the bank, it is found that the tree makes an angle of 60° at that point with respect to this bank.
Here AB is the width of the river
In △ABC,
tan C = \frac{AB}{BC}
or, \tan 60^{\circ}=\frac{A B}{7 \sqrt{3}}
∴ √3 = \frac{A B}{7 \sqrt{3}}
∴ AB = 7√3.√3 = 7 x 3 = 21 m
∴ Width of the river = 21m.
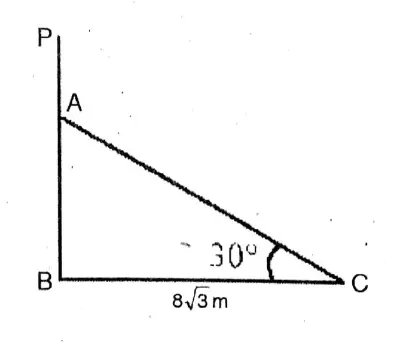
Question 8. A telegraph post is bent at a point above the ground due to a storm. Its top just meets the ground at a distance of 8 √3 metres from its foot and makes an angle of 30°. Let us write by calculating at what height the post is bent and what is the height of the post.
Solution:
The telegraph post is bent at a point above the ground due to a storm. Its top just meets the ground at a distance of 8 √3 metres from its foot and makes an angle of 30°.
Here PB is the height of the post which is bent at A & its top just meets the ground at C, at a distance of 8√√3 m from the foot of the post.
∴ PA = AC, ∠c = 30°
In △ABC,
tan C = \(\frac{AB}{BC}\)
or, tan30° = \(\frac{A B}{8 \sqrt{3}}\)
or, \(\frac{1}{\sqrt{3}}=\frac{A B}{8 \sqrt{3}}\)
∴ \(A B=\frac{8 \sqrt{3}}{\sqrt{3}}=8 \mathrm{~m}\)
Now, sin30° = \(\frac{AB}{AC}\)
or, \(\frac{1}{2}\) = \(\frac{8}{AC}\)
∴ AC = 8 x 2 = 16 m
∴ PA = AC = 16 m
Total height of the post = 16 + 8 = 24 m and the post bent at a height of 8m from the ground.
Question 9. Two houses stand just on opposite sides of the road of our village. A ladder that stands against the wall of the first house is at a distance of 6 metres from the house and makes an angle of 30° with the horizontal line. But if the ladder stands against the wall of the second housekeeping its foot at the same point, it makes an angle of 60° with the horizontal line.
1. Let us find the length of the ladder.
2. Let us write by calculating, the distance of the foot of the ladder from the foot of the wall of the second house.
3. Let us find the width of the road.
4. Let us find the height where the top of the ladder is fixed against the wall of the second house.
Solution:
Given
Two houses stand just on opposite sides of the road of our village. A ladder that stands against the wall of the first house is at a distance of 6 metres from the house and makes an angle of 30° with the horizontal line. But if the ladder stands against the wall of the second housekeeping its foot at the same point, it makes an angle of 60° with the horizontal line.
Here AB abd CD are two houses, on the opposite side of the road BD.
P is a point on the road, which is at a distance of 6 m from the foot of the 1st house AP is the length of the ladder.

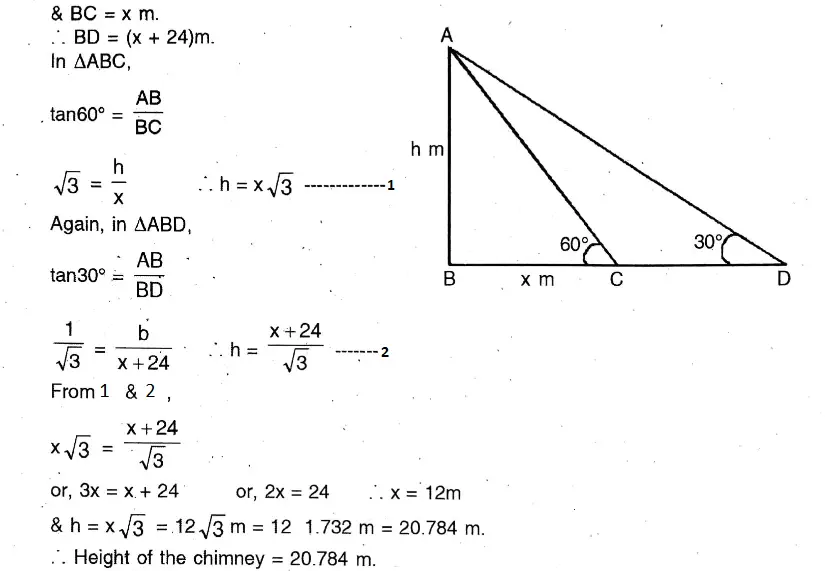
Question 10. If the angle of elevation of the top of a chimney from a point on the horizontal plane passing through the foot of the chimney is 60° and the angle of elevation from another point on the same plane at a distance of 24 metres from the first point is 30°, let us write by calculating the height of the chimney. [Let us find the approximate value correct up to three decimal places, assuming √3 = 1.732 (approx)].
Solution:
If the angle of elevation of the top of a chimney from a point on the horizontal plane passing through the foot of the chimney is 60° and the angle of elevation from another point on the same plane at a distance of 24 metres from the first point is 30°
Let AB is the height of the chimney = h m
Question 11. The length of the shadow of a post becomes 3 metres smaller when the angle of elevation of the sun increases from 45° to 60°. Let us find the height of the post. [Let us find the approximate value correct up to three decimal places, assuming √3 = 1.732 (approx)].
Solution:
The length of the shadow of a post becomes 3 metres smaller when the angle of elevation of the sun increases from 45° to 60°
Let AB = height of the post = h m.
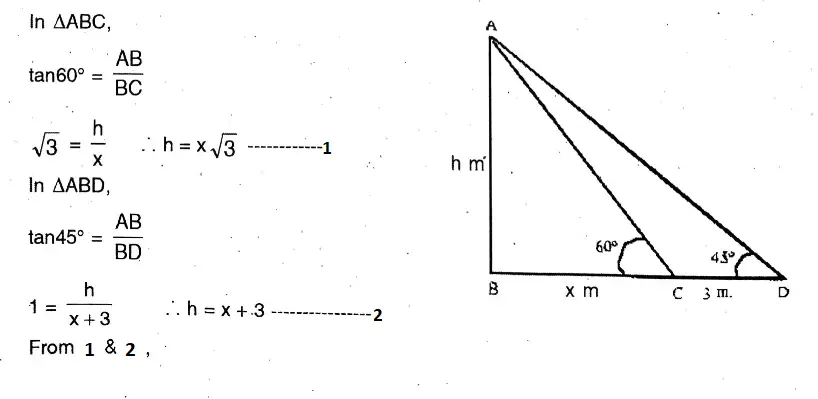
x√3 = x + 3
or, x√3 – x = 3 or x(√3 – 1) = 3
∴ x=\frac{3}{\sqrt{3}-1}=\frac{3(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}
∴ x=\frac{3(\sqrt{3}+1)}{3-1}=\frac{3(\sqrt{3}+1)}{2}
∴ h=x+3=\frac{3(\sqrt{3}+1)}{2}+3=\frac{3 \sqrt{3}+3+6}{2}=\frac{9+3 \sqrt{3}}{2}
= \frac{9+3 \times 1.732}{2}=\frac{9+5.196}{2}=\frac{14.196}{2}=7.098 \mathrm{~m}
∴ Height of the post = 7.098 m.
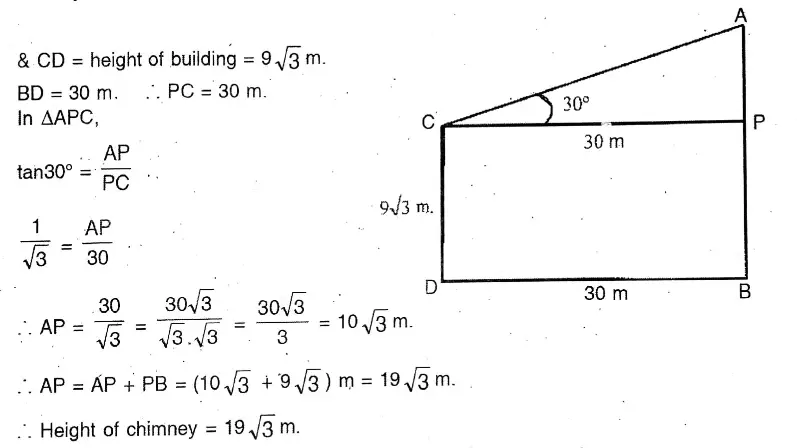
Question 12. When the top of a chimney of a factory is seen from a point on the roof of the three-storied building of 9 √3 metres in height, the angle of elevation is 30°. If the distance between the factory and the chimney is 30 metres, let us write by calculating the height of the chimney.
Solution:
When the top of a chimney of a factory is seen from a point on the roof of the three-storied building of 9 √3 metres in height, the angle of elevation is 30°. If the distance between the factory and the chimney is 30 metres
Let AB = height of the chimney
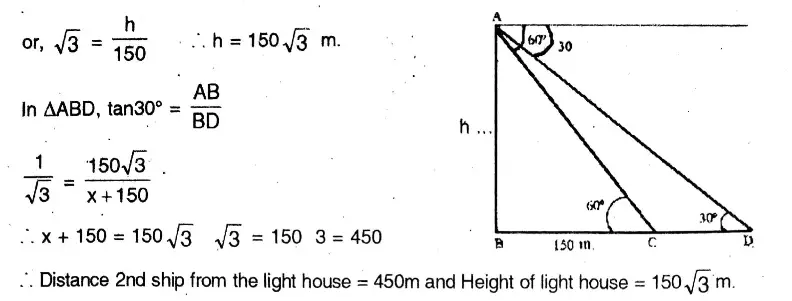
Question 13. The bottom of a lighthouse and the bottom of the mast of two ships are on the same straight line and the angles of depression from the lighthouse at the bottom of the mast of the two ships are 60° and 30° respectively. If the distance between the points at the bottom of the lighthouse and the bottom of the mast of the first ship is 150 metres, let us write by calculating, how far will the mast of the other ship from the lighthouse and what the height of the lighthouse will be.
Solution:
The bottom of a lighthouse and the bottom of the mast of two ships are on the same straight line and the angles of depression from the lighthouse at the bottom of the mast of the two ships are 60° and 30° respectively. If the distance between the points at the bottom of the lighthouse and the bottom of the mast of the first ship is 150 metres,
Let AB is the height of lighthouse = h m
& C & D are the position of two ships.
In ΔABC,
tan60° = AB/BC
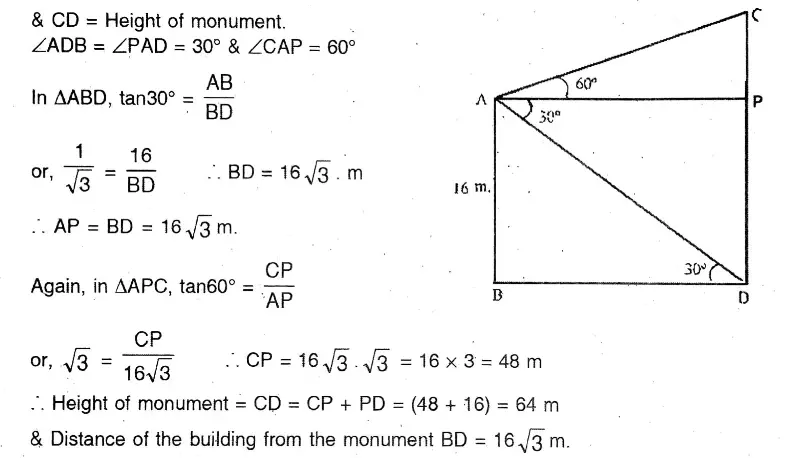
Question 14. From a point on the roof of a storied building, the angle of elevation of the top of a monument and that of the angle of depression of the foot of the monument are 60° and 30° respectively. If the height of the building is 16 metres, let us write by calculating the height of the monument and the distance of the building from the monument.
Solution:
From a point on the roof of five five-story buildings, the angle of elevation of the top of a monument and that of the angle of depression of the foot of the monument are 60° and 30° respectively. If the height of the building is 16 metres,
Let AB 16 m Height of the building
Question 15. I am flying a kite having a length of thread of 250 metres; when the thread makes an angle of 60° with the horizontal line, and when the thread makes an angle of 45° with the horizontal line. Let us write by calculating in each case what is the height of the kite from me. Let us find in which of the two cases will the kite be at a greater height from the other.
Solution:
I am flying a kite having a length of thread of 250 metres; when the thread makes an angle of 60° with the horizontal line, and when the thread makes an angle of 45° with the horizontal line.
In both cases A is the position of a Kite of different heights
AB = length of thread = 250 m (Both cases)
In 1st case, angle of elevation = 60°, & the height of Kite = AC
∴ In △ABC,
Sin60° = \(\frac{AC}{AB}\)
\(\frac{\sqrt{3}}{2}=\frac{A C}{250}\)∴ \(A C=\frac{250 \sqrt{3}}{2}=125 \sqrt{3} \mathrm{~m}\)
In 2nd case, angle of elevation = 45° & the height of Kite = AC
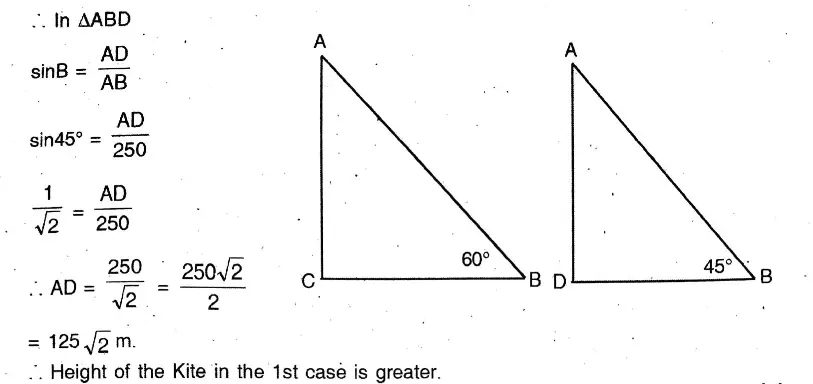
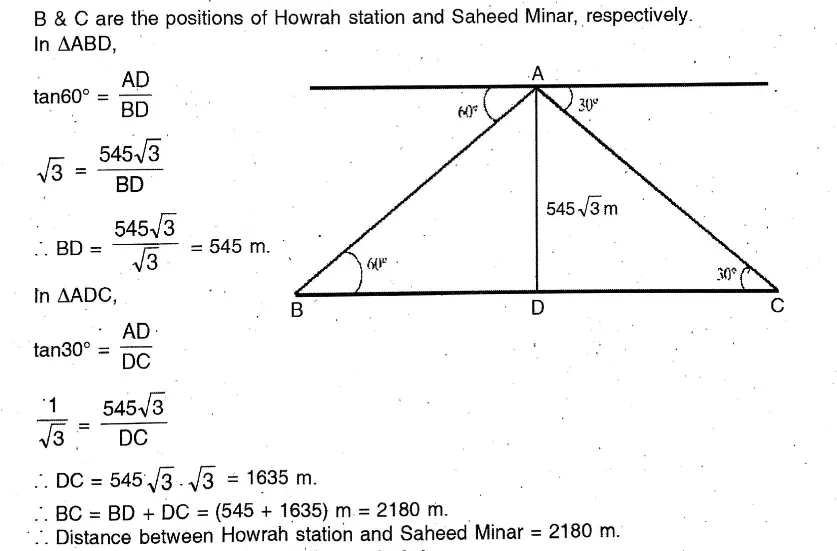
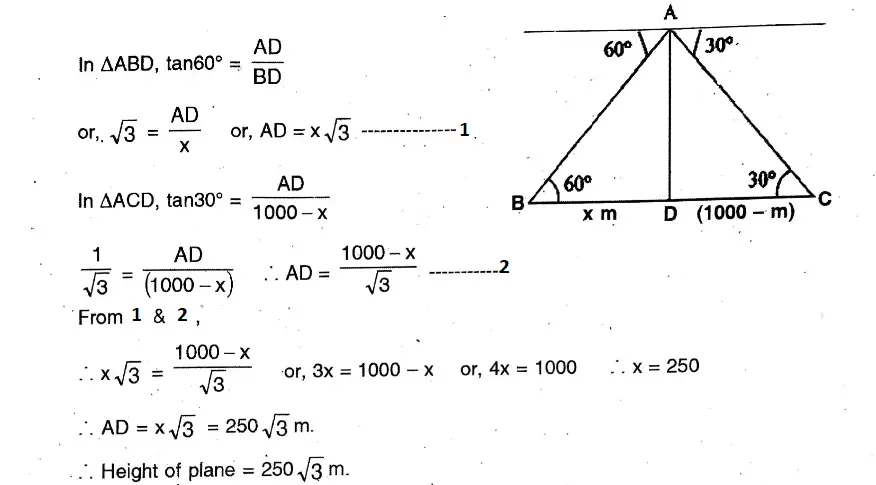
Question 16. A passenger of an aeroplane observes that Howarh station is on one side of the plane and Saheed Minar is just on the opposite side. The angles of depression of Howrah station and Saheed Minar from the passenger of the aeroplane are 60° and 30° respectively. If the aeroplane is at a height of 545 √3 metres at that time, let us find the distance between Howrah station and Saheed Minar.
Solution:
A passenger of an aeroplane observes that Howarh station is on one side of the plane and Saheed Minar is just on the opposite side. The angles of depression of Howrah station and Saheed Minar from the passenger of the aeroplane are 60° and 30° respectively. If the aeroplane is at a height of 545 √3 metres at that time
Let the height of the plane AD = 545 √3 m.
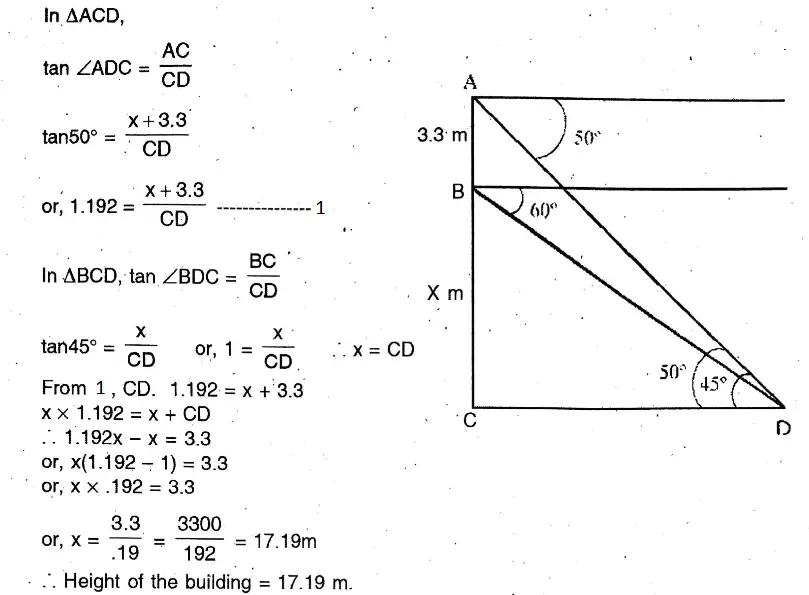
Question 17. The length of the flag on the roof of the three-storied building is 3.3 metres. From any point of the road, the angle of elevation of the top of the second tower is 60°, let us write by calculating what is the angle of elevation of the top of the second tower from the foot of the first.
Solution:
The length of the flag on the roof of the three-storied building is 3.3 metres. From any point of the road, the angle of elevation of the top of the second tower is 60°,
Let BC is the height of the building = x m.
& AB The length of flag = 3.3 m
∠ADC = 50°; ∠BDC = 45°
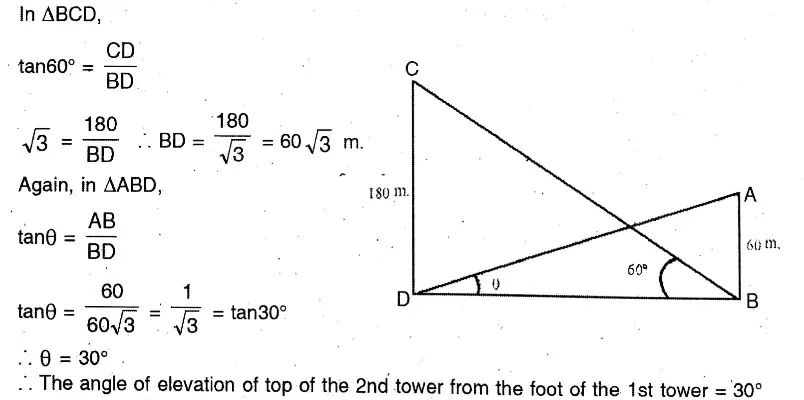
Question 18. The heights of the two towers are 180 metres and 60 metres respectively. If the angle of elevation of the top of the first tower from the foot of the second tower is 60°, let us write by calculating what is the angle of elevation of the top of the second tower from the foot of the first.
Solution:
The heights of the two towers are 180 metres and 60 metres respectively. If the angle of elevation of the top of the first tower from the foot of the second tower is 60°,
Let CD and AB be two towers of heights 180 m & 60 m respectively. In ABCD,
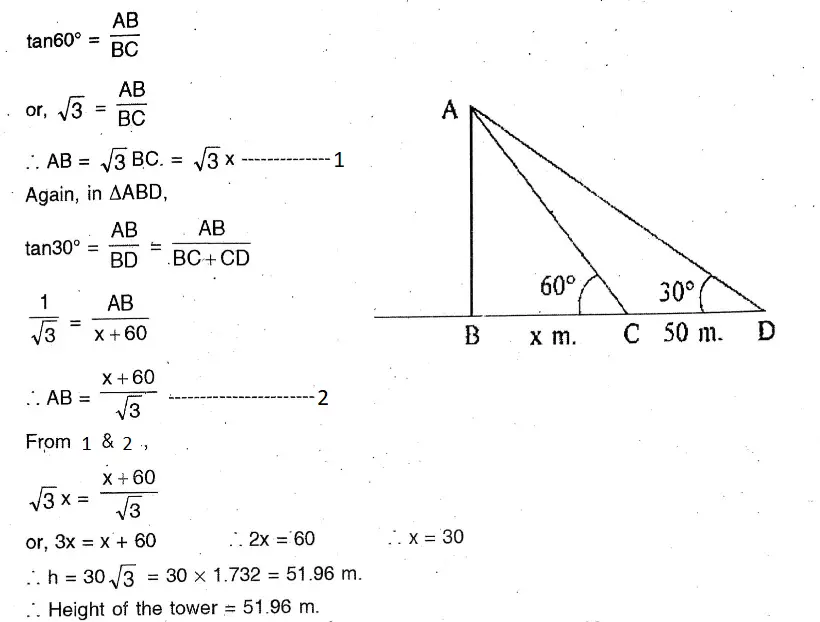
Question 19. The length of the shadow of a tower standing on the ground is found to be 60 metres more when the sun’s angle of elevation changes from 30° to 60°, let us find the height of the chimney.
Solution:
The length of the shadow of a tower standing on the ground is found to be 60 metres more when the sun’s angle of elevation changes from 30° to 60
Let AB = height of the tower – hm.
In ΔABC,
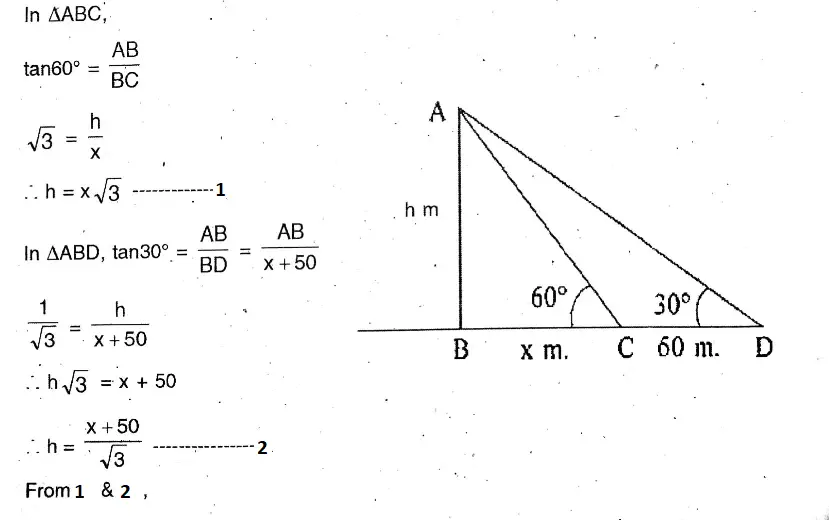
Question 20. From a point on the same plane along the horizontal line passes through the foot of a chimney, the angle of elevation of the top of the chimney is 30° and the angle of elevation of the top of the chimney is 60° at a point on the same straight line proceeding 50 metres nearer to the chimney. Let us write by calculating the height of the chimney.
Solution:
From a point on the same plane along the horizontal line passes through the foot of a chimney, the angle of elevation of the top of the chimney is 30° and the angle of elevation of the top of the chimney is 60° at a point on the same straight line proceeding 50 metres nearer to the chimney.
Let the height of the chimney = be AB = h m.
x√3 =x+50/√3
or, 3x = x + 50
or, 2x = 50
∴ x = 25 m.
h=x√3 = 25√3 m.
∴ Height of chimney = 25√3 m.
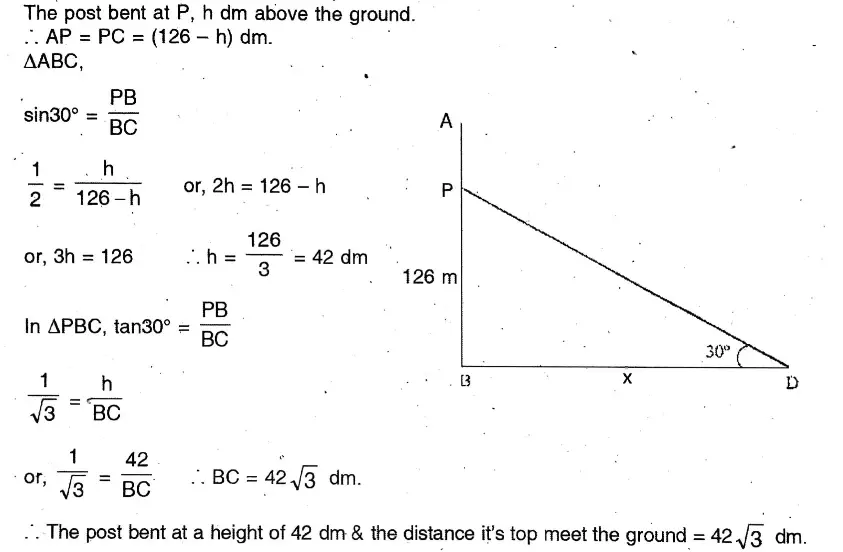
Question 21. A vertical post of 126 dm height was bent at some point above the ground and it just touched the ground making an angle of 30° with the ground. Let us write by calculating at what height was the post bent and at what distance it met the ground from the foot of the post.
Solution:
A vertical post of 126 dm height was bent at some point above the ground and it just touched the ground making an angle of 30° with the ground.
Let AB Height of the post = 126 dm.
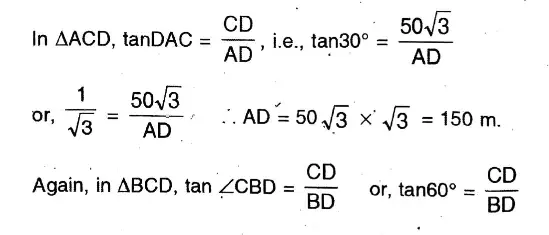
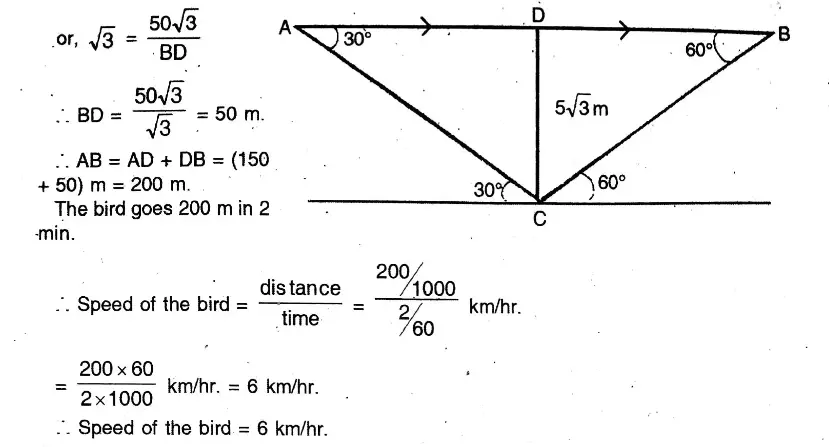
Question 22. Mohit, standing in the midst of a field, observes a flying bird in his north at an angle of elevation of 30° and after 2 minutes he observes the bird in his south at an angle of elevation of 60°. If the bird flies in a straight line all along at a height of 50√3 metres, let us find its speed in kilometres per hour.
Solution:
Mohit, standing in the midst of a field, observes a flying bird in his north at an angle of elevation of 30° and after 2 minutes he observes the bird in his south at an angle of elevation of 60°. If the bird flies in a straight line all along at a height of 50√3 metres,
Mohit standing at ‘C’ on the ground observes a bird in flying along AB from North to South at a height CD = 50√3 m above the ground.
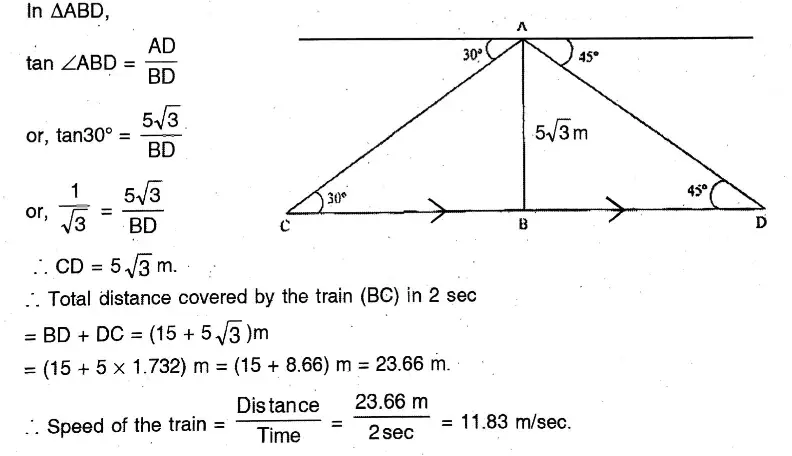
Question 23. Amitadidi standing on a railway overbridge of 5√3 metres height observed the engine of the train from one side of the bridge at an angle of depression of 30°. But just after 2 seconds, she observed the engine at an angle of depression of 45° from the other side of the bridge. Let us find the speed of the train in metres per second.
Solution:
Amitadidi standing on a railway overbridge of 5√3 metres height observed the engine of the train from one side of the bridge at an angle of depression of 30°. But just after 2 seconds, she observed the engine at an angle of depression of 45° from the other side of the bridge.
Let Amita Didi stand at A on the over bridge, which is at a height of 5√3 m from the ground. A train is moving from B to C.
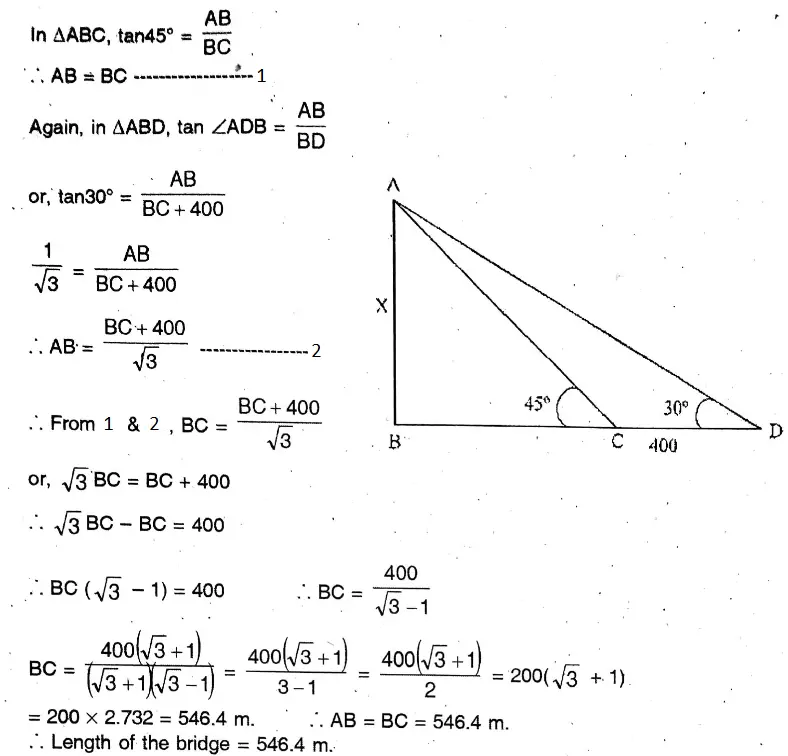
Question 24. A bridge is situated at a right angle to the bank of the river. If one moves away a certain distance from the birdge along this side of the river, the other end of the bridge is seen at an angle of 45° and if someone moves a further distance of 400 metres in the same direction, the other end is seen at an angle of 30°. Let us find the length of the bridge.
Solution: Let AB = length of the bridge.
Question 25. A house is situated at a right angle to the bank of the river. If one moves away a certain distance from the bridge along this side of the river, the other end of the bridge is seen at an angle of 45° and if someone moves a further distance of 400 metres in the same direction, the other end is seen at an angle of 30°. Let us find the length of the chimney and the distance between the brick kiln and the house.
Solution:
A house is situated at a right angle to the bank of the river. If one moves away a certain distance from the bridge along this side of the river, the other end of the bridge is seen at an angle of 45° and if someone moves a further distance of 400 metres in the same direction, the other end is seen at an angle of 30°.
Let AB & CD be the heights of the house & the chimney respectively. AB 15m, ED 15 m.
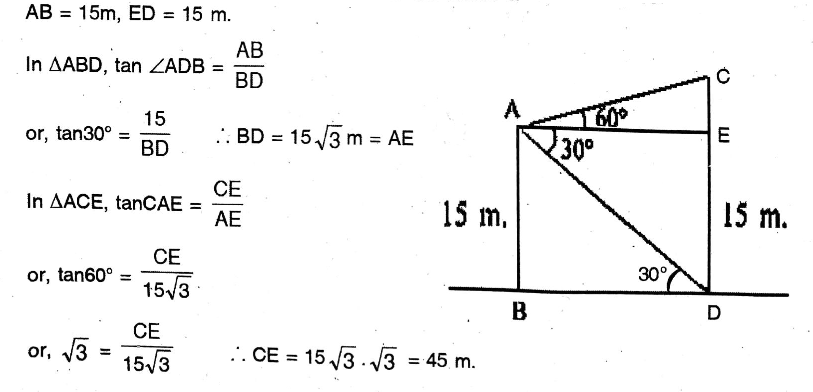
:. CD = CE+ED
= (45+ 15) m
= 60 m.
∴ The height of the chimney = 60 m & the distance between the brick kiln and the house = BD = 15.√3 m. Ans.
Question 26. If the angle of depression of two consecutive milestones on a road from an aeroplane is 60° and 30° respectively, let us find the height of the aeroplane,
1. when the two milestones stand on opposite sides of the aeroplane,
2. when the two milestones stand on the same side of the aeroplane.
Solution:
1. In 1st case A is the position of the plane & B & C are two consecutive milestones on the opposite side of the plane.
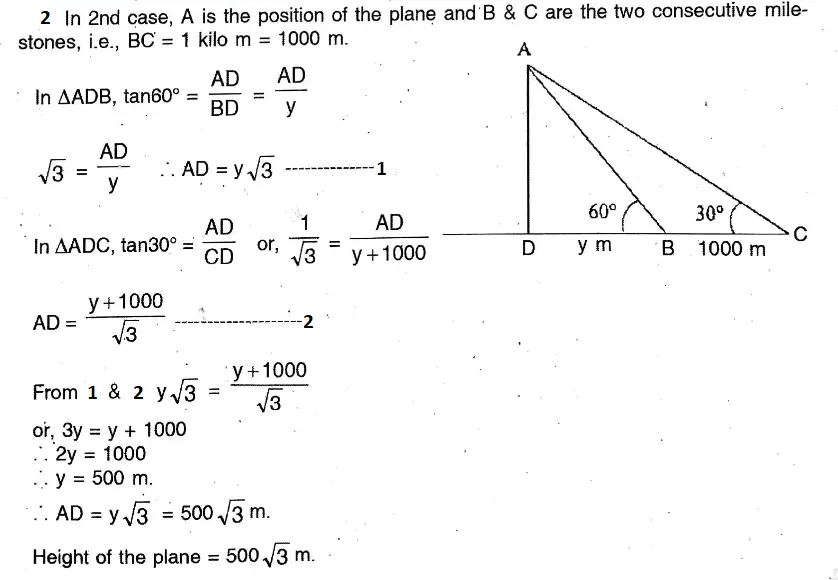
Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 Multiple Choice Question
Question 1. If the angle of elevation of the top of the mobile tower from a distance of 10 metres from its foot is 60°, then the height of the tower is
1. 10 metres
2. 10√3 metres
3. metres √3
4. 100 metres
Solution: tan60° = AB/BC
or, √3 = AB/10 ∴AB = 10√3 m.
Answer. 2. 10√3 metres
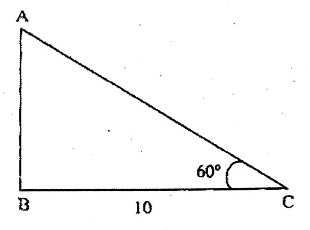
Question 2. In the diagram beside, the value is
1. 30°
2. 45°
3. 60°
4. 75°
Solution: tanθ = AB/BC
= 5/5√3
= tan30°
∴ 0 = 30°
Answer. 1. 30°
West Bengal Board Class 10 Math Book Solution In English
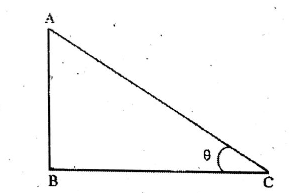
Question 3. At what angle an observer observes a box lying on the ground from the roof of the three-storied building so that the height of the building is equal to the distance of the box from the building?
1. 15°
2. 30°
3. 45°
4. 60°
Solution: tanθ = AB/BC
= 1
= tan45°
∴ 0 = 45°
Answer. 3. 45°
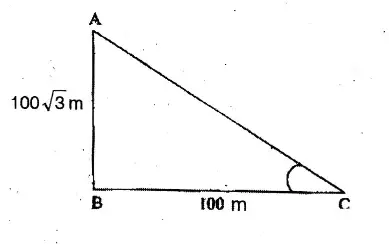
Question 4. The height of the tower is 100 √3 metres. The angle of elevation at the top of a tower from a point at a distance of 100 metres of the foot of the tower is
1. 30°
2. 45°
3. 60°
4. None of these
Solution: tanθ = AB/BC
100√3m/100=
= √3
tanθ = tan60°
Answer. 3. 60°
Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 True Or False
1. In AABC, ZB = 90°, if ZAB = BC, then C = 60°.
False
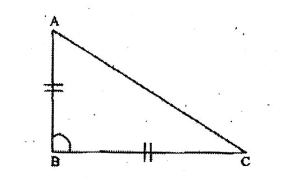
2. PQ is the height of a building OR is the base, and the angle of depression from a point P at point R is ZSPR. So, ZSPR = <PRQ.
True
Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 Fill In The Blanks
1. If the sun’s angle of elevation increases from 30° to 60°, the length of the shadow of a post Decreases (decreases/increases)
2. If the angle of elevation of the sun is 45°, then the length of shadow and length of post is Equal.
3. If the angle of elevation of the sun is Greater than 45°, the length of the shadow of the tower will be less than the height of the tower.
Chapter 25 Application Of Trigonometric Ratios Heights And Distances Exercise 25.1 Short Answers
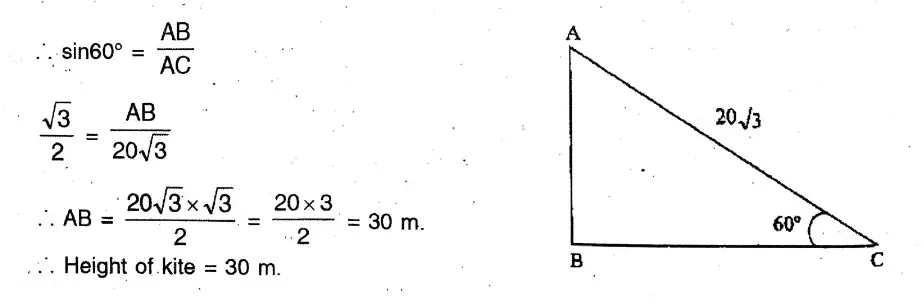
Question 1. If the angle of elevation of a kite is 60° and the length of the thread is 20√3 metres, let us calculate the height of the kite above the ground.
Solution.
If the angle of elevation of a kite is 60° and the length of the thread is 20√3 metres,
Let the height of the kite = be AB & length of the thread = be 20√3 m.
Question 2. AC is the hypotenuse with a length of 100 metres of a right-angled triangle ABC and if AB = 50 √3 metres, let us find the value of ZC.
Solution.
AC is the hypotenuse with a length of 100 metres of a right-angled triangle ABC and if AB = 50 √3 metres
AC hypotenuse = 100 m.

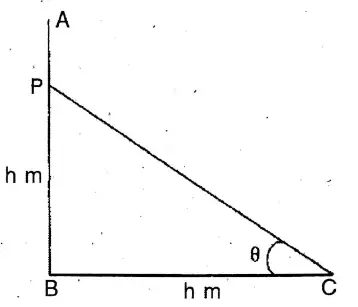
Question 3. A tree breaks due to a storm and its top touches the ground in such a manner that the distance from the top of the tree to the base of the tree and present height are equal. Let us calculate how much angle is made by the top of the tree with the base.
Solution.
A tree breaks due to a storm and its top touches the ground in such a manner that the distance from the top of the tree to the base of the tree and present height are equal.
AB is the height of the tree.
∴ tanθ = PB/BC = h/h = 1
∴ tanθ = 1 = tan45°
∴ 0 = 45°
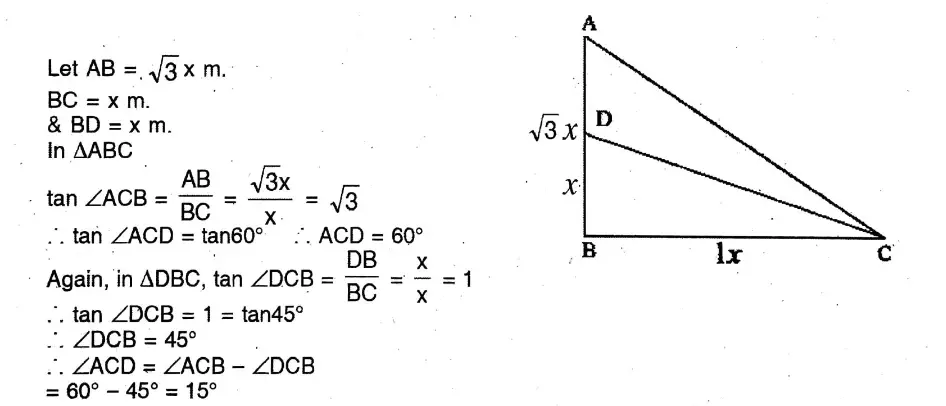
Question 4. In the right-angled triangle ABC, B = 90°, D is such a point on AB that AB: BC: BD = √3:1:1, let us find the value of ∠ACD.
Solution.
In the right-angled triangle ABC, B = 90°, D is such a point on AB that AB: BC: BD = √3:1:1
AB: BC BD = √3:1:1
Question 5. If the ratio between the length of the shadow of a tower and the height of the tower is √3:1, let us find the angle of elevation of the sun.
Solution.
If the ratio between the length of the shadow of a tower and the height of the tower is √3:1,
Let BC: AB = √3:1