Ganit Prakash Class 10 Solutions Pdf In English
Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.2
Question 1. Per day selling prices (in Rs.) of Madhu’s uncle’s shop for the last week were 107, 201, 92, 52, 113, 75, and 195; let us find the median of the selling prices.
Solution: Selling prices (in Rs.) per day are 107, 207, 92, 52, 113, 75, and 195. To find the median of the selling prices first arrange them in ascending order, we get 52, 75, 92,107, 113, 195, and 210.
Here n = 7 (odd).
∴ Median = (7+1/2) th term
= 4th term
= 107
∴ Median Rs. 107
Read and Learn More WBBSE Solutions For Class 10 Maths
Question 2. If the ages (in years) of some animals are 6, 10, 5, 4, 9, 11, 20, or 18; let us find the median of ages.
Solution: Ages (in years) of some animals are 6, 10, 5, 4, 9, 11, 20, 18.
Arranging in ascending order,
we get 4, 5, 6, 9, 10, 11, 18, 20
Hére n = 8 (even).
Median = 1/2 {n/2 th term + (n/2 + 1) term}
= 1/2 (4th term + 5th term)
= 1/2(9+10)
= 19/2
= 9.5 years
“WBBSE Class 10 Maths Statistics Mean, Median, Mode Exercise 26.2 solutions”
Question 3. The marks obtained by 14 students are 42, 51, 56, 45, 62, 59, 50, 52, 55, 64, 45, 54, 58, and 60; let us find the median of the marks obtained.
Solution: The marks obtained by 14 students are 42, 51, 56, 45, 62, 59, 50, 52, 55, 64, 45, 54, 58, and 60.
Arranging in ascending order, we get 42, 45, 45, 50, 51, 52, 54, 55, 56, 56, 58, 59, 60, 62.
Here, n = 14 (even).
Median = 1/2 {n/2 th term + (n/2 + 1) term}
= 1/2 {7th term + 8th term}
= 1/2(54+55)
= 1/2 x 109
= 54.5
∴ Median = 54.5

Question 4. Today the scores of the cricket match in our locality are Let us find the median of scores in our cricket match.
Solution: By arranging the scores of the match
6 6 6 77777 88888 99999 10 10 11 11
Here n = 22 i.e., even.
∴ Median = 1/2 {n/2 th term + (n/2 + 1) term}
= 1/2 (11th term + 12th term}
= 1/2 (8+8)
= 1/2 x16
= 8
∴ Median = 8
“West Bengal Board Class 10 Maths Chapter 26 Statistics Mean, Median, Mode Exercise 26.2 solutions”
Question 5. Let us find the median weight from the following frequency distribution table of 70 students.
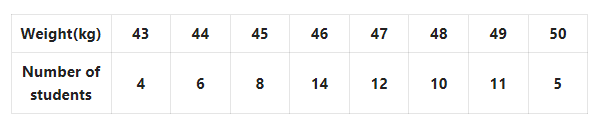
Solution:
Question 6. Let us find the median of the length of diameter from the following frequency distribution table of the length of the diameter of the pipe.

Solution:

Question 7. Let us find the median.
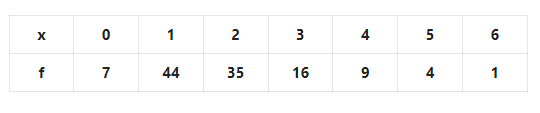
Solution:

“WBBSE Class 10 Statistics Mean, Median, Mode Exercise 26.2 solutions explained”
Question 8. The frequency distribution table of expenditures of tiffin allowances of 40 students is given below.
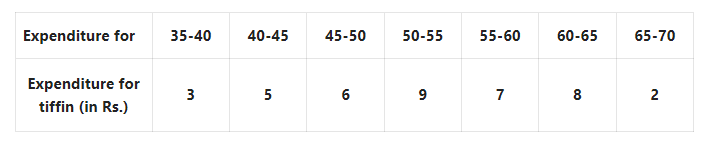
Let us find the median of tiffin allowance.
Solution:

Question 9. Let us find the median heights of students from the table below.

Solution:

Here, l – 150, c.f. = 35, f = 22, h = 5.
∴ median = \(\dot{\ell}+\left[\frac{\frac{n}{2}-c . f}{f}\right] \times h\)
= \(150+\left[\frac{50-35}{22}\right] \times 5\)
= \(150+\frac{15}{22} \times 5\)
= 150 + 3.4
median = 153.4 (approx)
“WBBSE Class 10 Maths Exercise 26.2 Statistics Mean, Median, Mode problem solutions”
Question 10. Let us find the median of data from the following frequency distribution table.

Solution:

Question 11. Let us find the median of the given data.

Solution:

Question 12. Let us find the median of the given data.

Solution:

Question 13. Let us find the median of the given data.
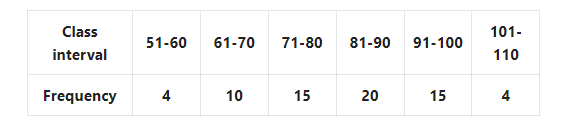
Solution:
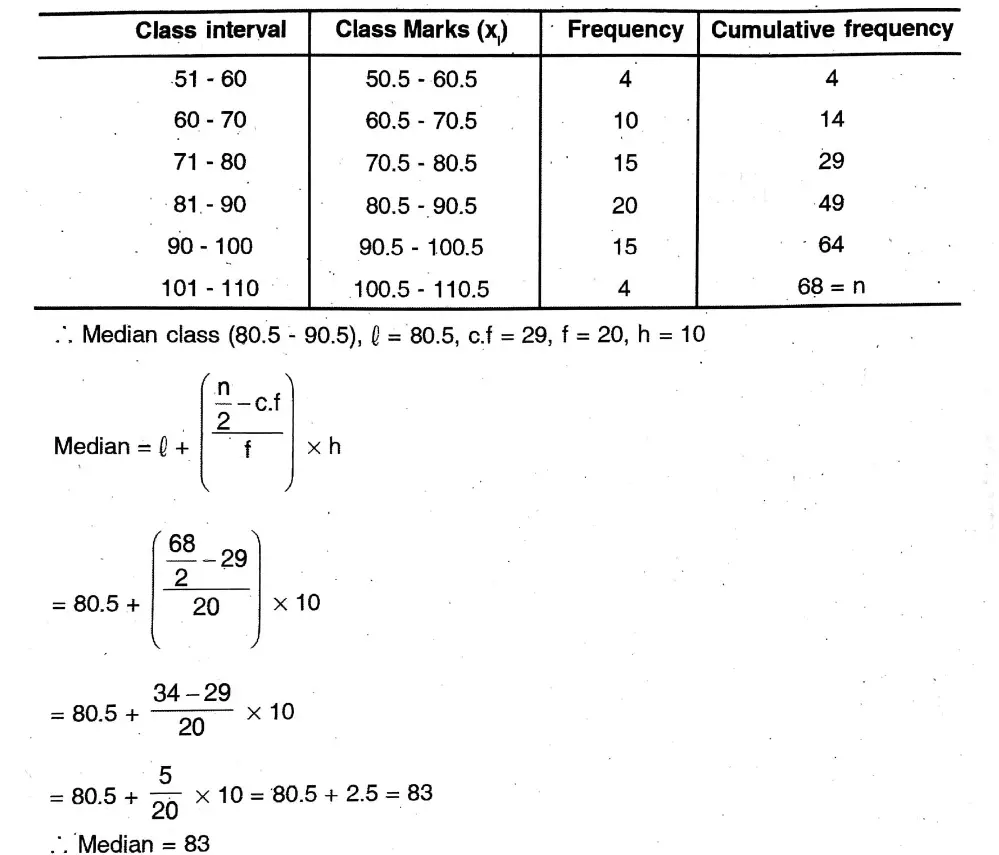
Question 14. Let us find the median of the given data.
Solution:

Question 15. If the median of the following data is 32, let us determine the values of x and y when the sum of the frequencies is 100.

Solution:

32 = \(\ell+\left(\frac{\frac{n}{2}-c . f}{f}\right) \times h\)
32 = \(30+\frac{50-(35+x)}{30} \times 10\)
32 – 30 = \(\frac{50-35-x}{3}\)
or, 6 = 15 – x ∴ x = 15 – 6 = 9
x + y = 25 ∴ y = 25 – 9 = 16
“Class 10 WBBSE Maths Exercise 26.2 Statistics Mean, Median, Mode step-by-step solutions”
Application 1. Let us draw less than type Ogive and greater than type Ogive and let us find the median of the following frequency distribution table.

solution:
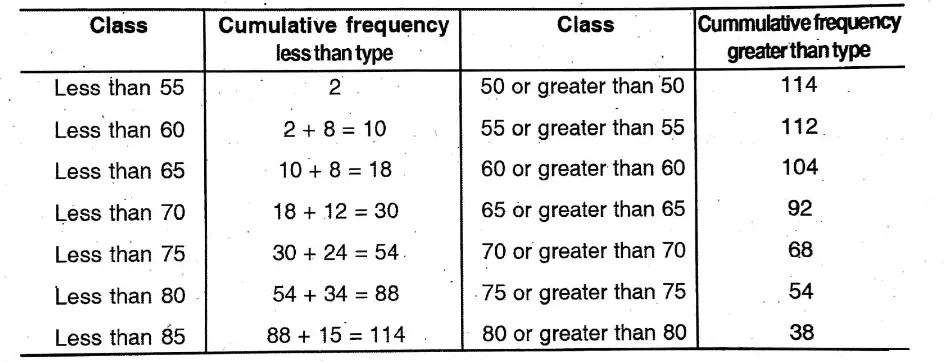
Assuming on graph paper along x-axis 1 small division 1 unit, & along y-axis 1 small division=1 unit, we draw greater than type Ogive & less than type Ogive. For greater than type Ogive plotting the points (50, 114), (55, 112), (60, 104), (65, 92), (70, 68), (75, 54), (80, 38).
And for less than type Ogive plotting the points (55, 2), (60, 10), (65, 18), (70, 30) (75, 54), (80, 88) & (85, 144) on graph paper, we join them.
The greater than type Ogive & less than type Ogive intersect each other at point P. Draw perpendicular PM on the x-axis from P which intersects. the x-axis at point M.
The co-ordinates of M = (75, 0)
∴ Median = 75.
