WBBSE Solutions For Class 10 Maths Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.4

West Bengal Board Class 10 Math Book Solution In English

Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4

Question 1. Paid amounts a day of our 16 friends for going to school and other expenditures are:

15, 16, 17, 18, 19, 17, 15, 15, 10, 17, 16, 15, 16, 18, 11

Let us find the mode of paid amounts of a day of our friends. 

Solution: Arranging the given data in ascending order, we get 10, 11, 15, 15, 15, 15, 16, 16, 16, 17, 17, 17, 17, 18, 19. We see 15 & 17 occur a maximum number of times.

∴ Mode = Rs. 15 & Rs. 17.

Read and Learn More WBBSE Solutions For Class 10 Maths

Question 2. The heights (cm) of some students in our class are given below. 131, 130, 130, 132, 131, 133, 131, 134, 131, 132, 132, 131, 133, 130, 132, 133, 135, 131, 135, 131, 130, 132, 135, 134, 133. Let us find the mode of the heights of students.

Solution: Arranging the given data in ascending order, we get

130, 130, 130, 130, 131, 131, 131, 131, 131, 131, 131, 132, 132, 132, 132, 132, 133, 133, 133, 134, 134, 135, 135, 135, 135.

Here 131 occurs a maximum number of times.

∴ Mode = 131 cm.

West Bengal Board Class 10 Math Book Solution In English

Question 3. Let us find the mode of data given below :

1. 8, 5, 4, 6, 7, 4, 4, 3, 5, 4, 5, 4, 4, 5, 5, 4, 3,3, 5, 4, 6, 5, 4, 5, 4, 2, 3, 4.

Solution: Arranging the given data in ascending order we get

2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 7, 8. 

Here 4 occurs a maximum number of times.

∴ Mode = 4

2. 15, 11, 10, 8, 15, 18, 17, 15, 10, 19, 10, 11,10, 8, 19, 15, 10, 18, 15, 3, 16, 14, 17, 2

Solution: Arranging the given data in ascending order we get,

2, 3, 8, 8, 10, 10, 10, 10, 10, 11, 11, 14, 15, 15, 15, 15, 15, 16, 17, 17, 18, 19, 19. 

Here 10 and 15 occur a maximum number of times.

∴ Mode = 10 and 15

Question 4. The frequency distribution table shows the selling prices of shoes from a special shoe shop company in our village.

Solution:

Here are 5 persons for size 4 & 5 persons for size 6.

∴ Mode = 4 & 6.

Question 5. Let us find the mode from the following frequency distribution table of the ages of examinees of an entrance examination.

Solution:

Here Modal class = (18 – 20)

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)     Here l = 18

= \(18+\left(\frac{75-45}{150-45-38}\right) \times h\)             f₁ = 75 

= \(18+\frac{30}{67} \times 2\)            f₂ = 38

Mode = 18 + 0.9 = 18.9 (approx)        h = 2

Question 6. Let us see the frequency distribution table of obtaining marks in a periodical examination of 80 students in a class and let us find the mode.

Solution:

Here, Modal class = (20 – 25)

l = 20, f₁ = 22, f₀ = 16, f₂ = 1, h = 5

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h=20+\frac{22-16}{44-11-11} \times 5\)

= \(20+\frac{6}{17} \times 5\)

= 20 + 1.76

Mode = 21.76 (approx)

 

Question 7. Let us find the mode of the frequency distribution table given below

Solution:

∴ Modal class = 15 – 20,

∴ l = 15, h = 5

f₁ = 28, f₀ = 18, f₂ = 17, h = 5

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)

= \(15+\frac{28-18}{56-18-15} 5\)

= \(15+\frac{10 \times 5}{21}\)

= 15 + 2.38

Mode = 17.38

 

Question 8. Let us find the mode of the frequency distribution table given below

Solution:

∴ Modal class = 75 – 84,

∴ l = 75, h = 9

f₁ = 32, f₀ = 19, f₂ = 12

∴ Mode = \(\ell+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)

= \(75+\frac{32-19}{64-19-12} \times 9\)

= \(75+\frac{13 \times 9}{33}\)

= 75 + 3.54

Mode = 78.54 (approx)

WBBSE Solutions Guide Class 10 Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4 Multiple Choice Questions

Question 1. The median of a given frequency distribution is found graphically with the help of 

1. Frequency curve
2. Frequency polygon
3. Histogram
4. Ogive

Answer. 4. Ogive

Question 2. If the mean of numbers 6, 7, x, 8, and y, is 9, then

1. x + y = 21
2. x + y = 19
3. x – y = 21
4. x – y = 19

Answer. 2. x + y = 19

Question 3. If 35 is removed from the data 30, 34, 35, 36, 37, 38, 39, 40 then the median increases by

1. 2
2. 1.5
3. 1
4. 0.5

Answer. 4. 0.5

Question 4. If the mode of data 16, 15, 17, 16, 15, x, 19, 17, 14 is 15, then the value of x is 

1. 15
2. 16
3. 17
4. 19

Answer. 1. 15

WBBSE Solutions Guide Class 10 Question 5. If the median of arranging the ascending order of data 8, 9, 12, 17, x + 2, x + 4, 30, 31, 34, 39, is 15, then the value of x is

1. 22
2. 21
3. 20
4. 24

Answer. 2. 21

WBBSE Solutions Guide Class 10 Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4 Fill In The Blanks

1. Mean, median, and mode are the measures of  Central tendency

2. x_1,x_2,x_3…….. x_{n is} x‾ _{, mean of} ax_1, ax_2, ax_{3…………} ax_{n is} ax¯

3. At the time of finding the arithmetic mean, the lengths of all classes are Equal.

WBBSE Solutions Guide Class 10 Chapter 26 Statistics Mean, Median, Ogive, Mode Exercise 26.4 Short Answers

Question 1

Let us find the difference between the upper-class limit in the median class and the lower-class limit of the modal class of the above frequency distribution table.

Solution: n = 77, n/2 = 38.5

Median class= 125-145

The upper limit of Median class = 145

Model class= 125-145

Lower class limit of Modal class = 125

∴ Required Difference 145 125 = 20.

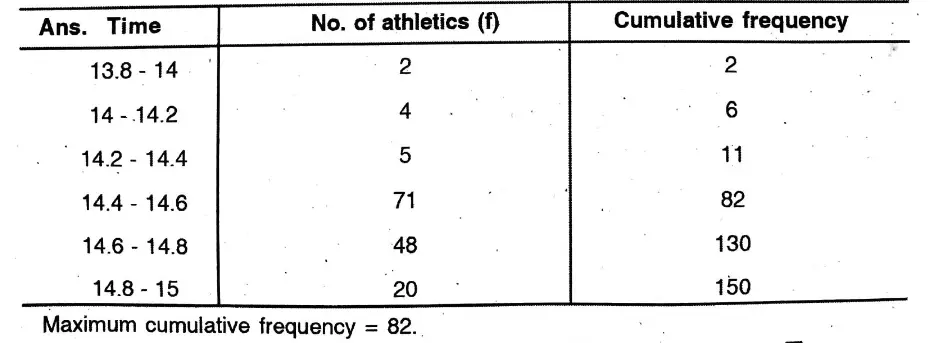
Question 2. The following frequency distribution shows the time taken to complete a 100-meter hurdle race of 150 athletics :

Let us find the difference between the upper-class limit of the modal class and the lower-class limit of the modal class.

Solution:

Question 3. The mean of a frequency distribution is 8.1, if Σf₁x₁= 132 + 5k and Σf₁ = 20, let us find the value of k.

Solution:

Given

The mean of a frequency distribution is 8.1, if Σf₁x₁= 132 + 5k and Σf₁ = 20

\(\frac{\sum f_i n_i}{\sum f_i}=8.1\) \(\frac{132+5 k}{20}=8.1\)

or, 132 + 5k = 162

∴ 5k = 30

∴ k = \(\frac{30}{5}\) = 6

 

Question 4. If u_i =x_i-25 / 10 Σf_iu_i = 20 and Σf_i = 100, let us find the value of x.

Solution:

If u_i =x_i-25 / 10 Σf_iu_i = 20 and Σf_i = 100

a = 25, h = 10

∴ \(\mathrm{n}=\mathrm{a}+\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{n}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\)

= \(25+10 \times \frac{20}{100}=25+2=27\)

Question 5.

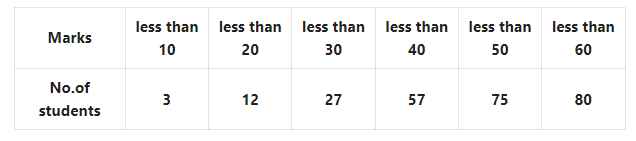
Let us write the modal class from the above frequency distribution table.

Solution:

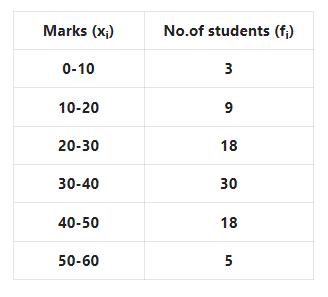
∴ Model Class = (30-40)