WBBSE Solutions For Class 10 Maths Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.1

West Bengal Board Class 10 Math Book Solution In English Chapter 26 Statistics Mean, Median, O Give, Mode Exercise 26.1

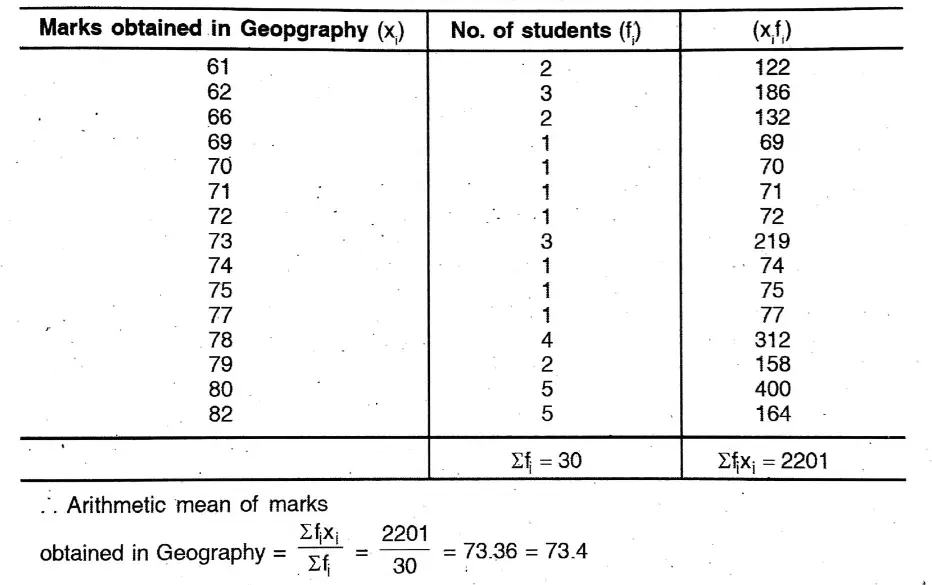
Application 1. The marks obtained by 30 students of the class of the Bishakha in Geography are :

60, 78, 80, 69, 73, 61, 82, 78, 79, 72, 78, 62, 80

71, 82, 73, 62, 80, 74, 78, 62, 80, 66, 70, 79, 75

Let us find the arithmetic mean of marks obtained in Geography. 

Solution: To find the Arithmetic mean of marks obtained in Geography

Read and Learn More WBBSE Solutions For Class 10 Maths

1. I have written the ages of my 40 friends in the table given below

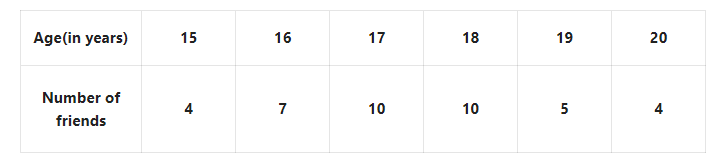
Solution:

∴ Average age = \(\frac{\Sigma f_{x_i}}{\Sigma f_i}=\frac{697}{40}=17.425\)

2. I have written the number of members in each of the 50 families of our village in the table given below

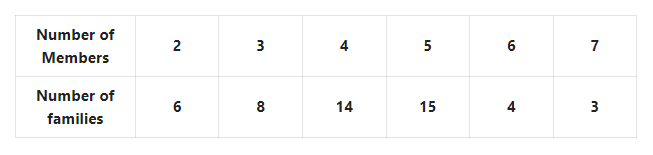
Solution:

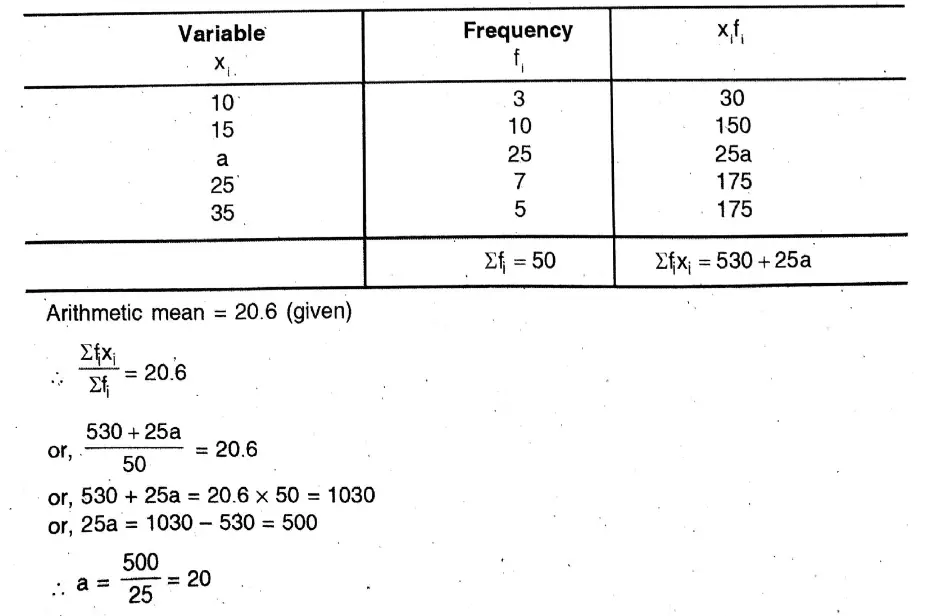
3. If the arithmetic mean of the data given below is 20.6, let us find the value of ‘a’.

Solution:

4. If the arithmetic mean of the distribution given below is 15, let us find the value of p.

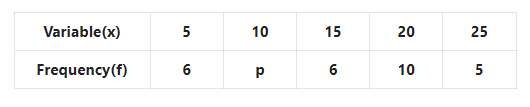
Solution:

5. Rahamatchacha will go to the retail market for selling mangoes kept in 50 packing boxes. Let us write the number of boxes contained for varying numbers of mangoes in the table given below.

Solution:

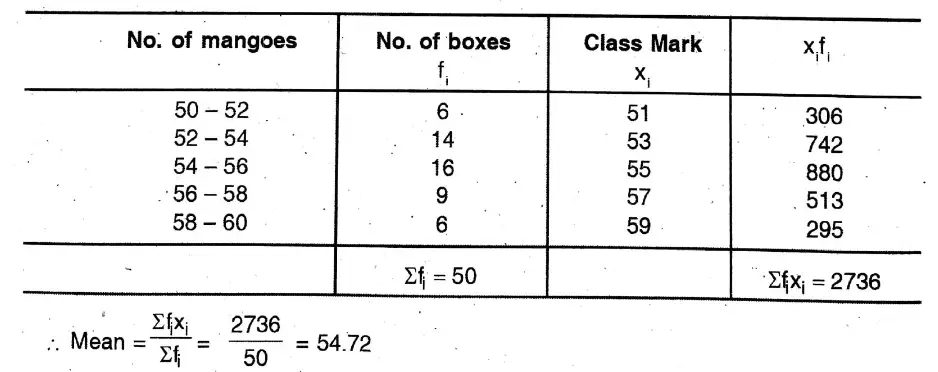
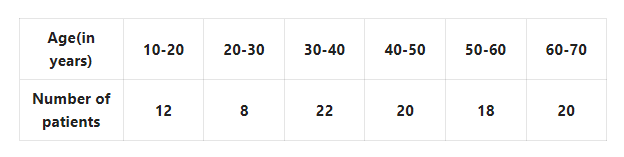
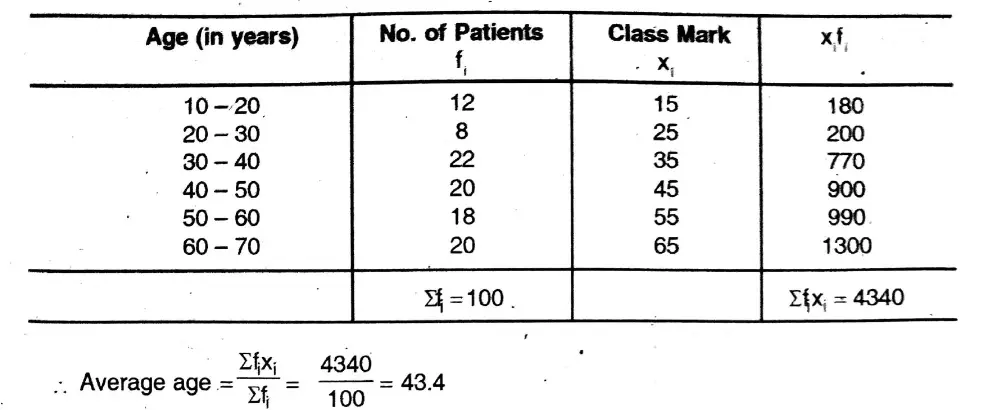
6. Mohidul has written the ages of 100 patients of a village hospital. Let us write by calculating the average age of 100 patients.

Solution:

7. Let us find the mean of the following data by the direct method.

Solution:

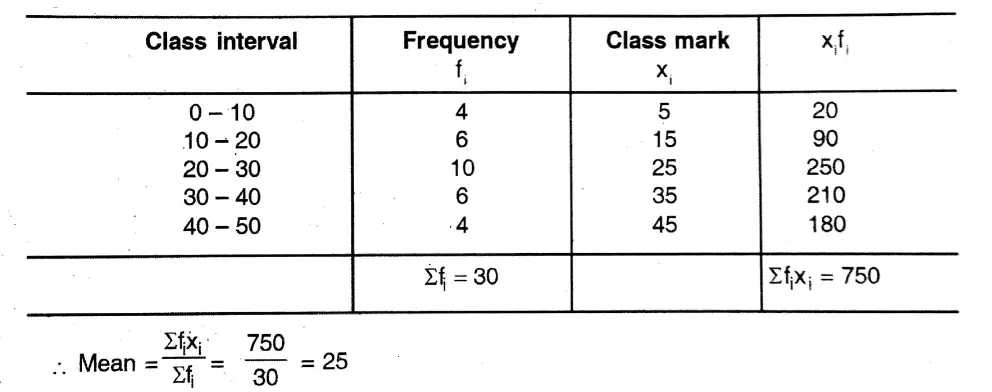
Question 8. Let us find the mean of the following data by the assumed mean method.

1.

Solution:

2.

Solution:

Question 9. Let us find the mean of the following data by step deviation method.

1.

Solution: Let assumed mean a = 75

μ_i = x_i-a/h, h

= 30-0= 60-30

= 90-60

μ_i =30

2.

Solution: Let assumed mean a = 35

μ_i = x_i-a/h , h

= 14-0

= 28-14

= 42-28

μ_i = 14

Question 10. If the mean of the following frequency distribution table is 24, let us find the value of p.

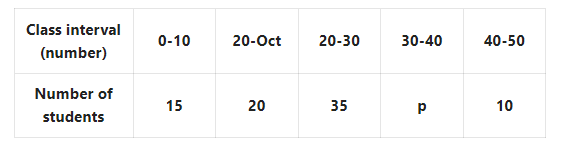
Solution:

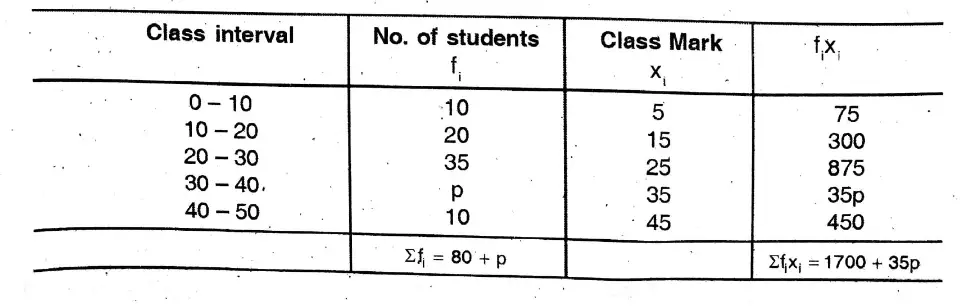
Here, mean = 24 (given)

∴ \(\frac{\Sigma \mathrm{f}_{\mathrm{i}_{\mathrm{i}}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\overline{\mathrm{x}}\)

⇒ \(\frac{1700+35 p}{80+p}=24\)

or, 1700 + 35p = 1920 + 24p

or, 35p – 24p = 1920 – 1700

or, 11p = 220

or, p = \(\frac{220}{11}\)

∴ p = 20

Question 11. Let us see the ages of the persons present in a meeting and determine their average age from the following table

Solution:

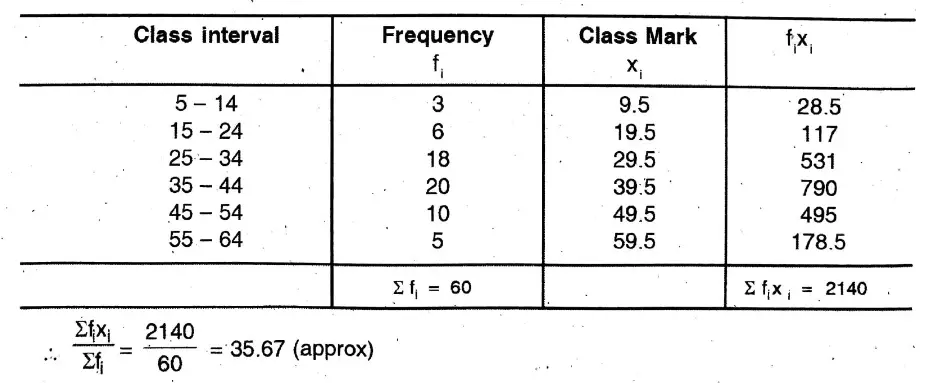
Question 12. Let us find the mean of the following data

Solution:

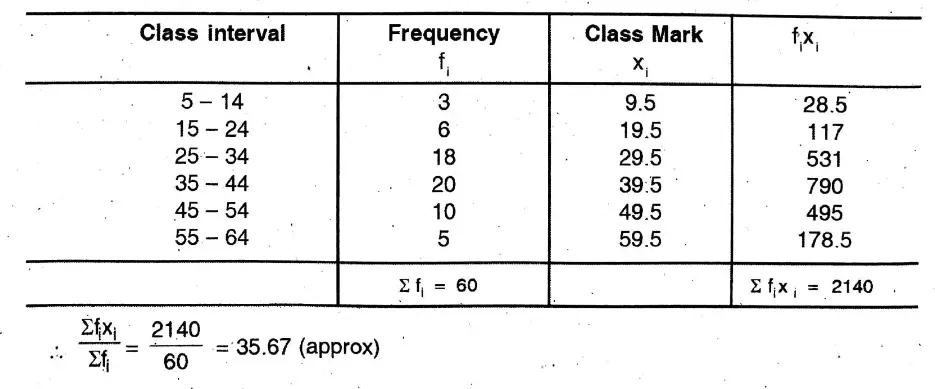
Question 13. Let us find the mean of marks obtained by girl students if their cumulative frequencies are as follows

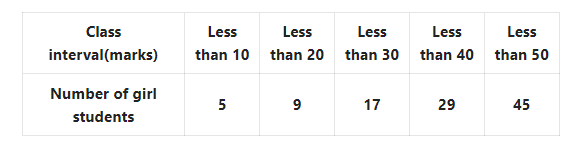
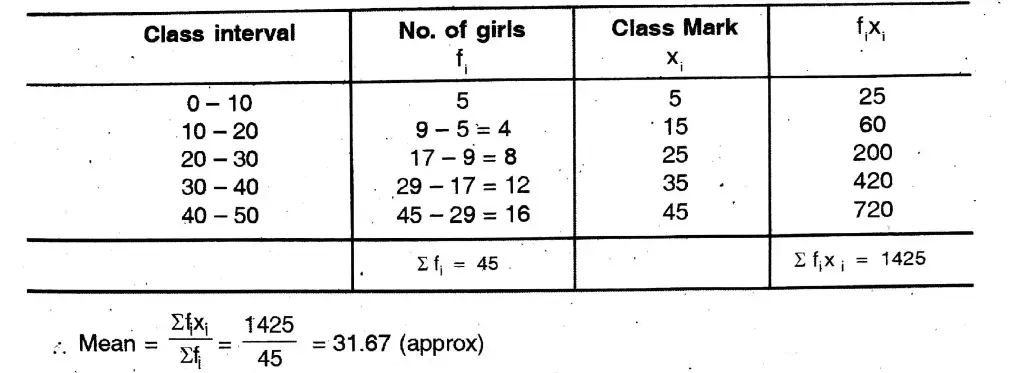
Solution:

Question 14. Let us find the mean of the marks obtained from 60 students from the table given below.

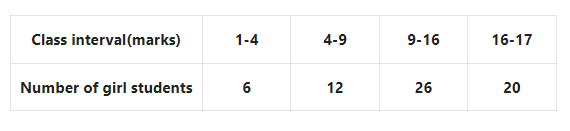
Solution:

Application 1. The points obtained by two kabaddi teams in different matches are

given below. Let us determine their median.

1. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

2. 6, 7, 8, 8, 9, 10, 15, 15, 16, 17, 19, 25

Solution:

1. Find the median

5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

Here no. of terms(n) = 11 (i.e., odd)

∴ Median = (11+1/2)^th value = 6th value = 10

2. Find the median 

6, 7, 8, 8, 9, 10, 15, 15, 16, 17, 19, 25 

Here no. of terms (n) = 12 (i.e., even)

∴ Required median = 1/2{(12/2)^th value + ((12/2 + 1)^th value}

= 1/2(6th value + 7th value)

= 1/2(10+15)

= 25/2

Required median  = 12.5

Application 2. Let us find the median from the following distribution table.

Solution:

Application 3. Let us see the following frequency distribution table and let us find the median.

Solution:

∴ x = \(\Sigma \boldsymbol{\Sigma}=80\)

∴ \(\frac{x}{2}\) = 40

The corresponding class of cumulative frequency just greater than 40 is (20 – 30)

∴ Required median class is (20 – 30)

∴ Required median = \(\ell+\left[\frac{\frac{n}{2}-c . f}{f}\right] \times h\)

= \(20+\left[\frac{40-18}{24}\right] \times 10\)          Here l = 20, c.f = 18

= \(20+\frac{22}{24} \times 10\)

=  \(\frac{n}{2}\) = 40

= 20 + 9.16 = 29.16   f = 24, h = 20

∴ Median = 29.17 (approx)

Application 4. If the median of the following data is 28.5, and the total frequency is 100, let us find the values of x and y.

Solution:

⇒ \(28.5=20+\frac{30-(5+x)}{20} \times 10\)

⇒ \(20+\frac{30-5-x}{2}\)

⇒ \(28.5=\frac{40+30-5-x}{2}\)

57 = 65 – x

∴ x = 65 – 57 = 8

From (1), x + y = 15

∴ y = 15 – x = 15 – 8 = 7

∴ x = 8  and y = 7