WBBSE Solutions For Class 10 Maths Chapter 3 Theorems Related To Circle Exercise 3.1
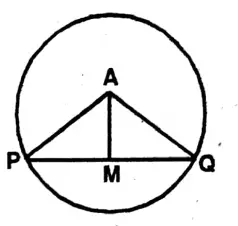
Question 1. Let us see the adjoining figure of the circle with center O and write the rate which is situated in the segment PAQ.
Answer:
In the circle with center O, OP, OA, OC, and OQ are the radii in the A segment PAQ.
Question 2. Let us write in the following ![]() by understanding it.
by understanding it.
1. In a circle, there is ![]() number of points.
number of points.
Answer: Infinite.
Read and Learn More WBBSE Solutions For Class 10 Maths
2. The greatest chord of the circle is ![]()
Answer: Diameter.
3. The chord divides the circular region into two ![]()
Answer: Sector.
4. All diameters of the circle pass-through ![]()
Answer: Centre.
5. If two segments are equal, then their two arcs are ![]() in length.
in length.
Answer: Equal.
6. The sector of the circular region is the region enclosed by the arc and the two ![]()
Answer: Radii.
7. The length of the line segment joining the point outside the circle and the center is ![]() than the length of the radius.
than the length of the radius.
Answer: Greater.
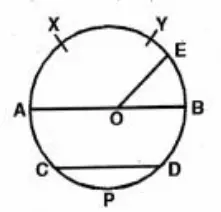
Question 3. With the help of scale and pencil, compass let us draw a circle and indicate centre, chord diameter, radius, major arc, minor arc on it
Answer: Centre O
Chord – CD
Diameter – AB
Radius OE = OA = OB
Minor arc – \(\overline{x y}\)
Major arc – \(\overline{x p y}\)
Chapter 3 Theorems Related To Circle Exercise 3.1 True or False
1. The circle is a plane figure.
Answer: Circle is a rectilinear figure
True
2. The segment is a plane region.
Answer: A segment of a circle is a rectilinear figure.
True
3. The sector is a plane region.
Answer: The sector is rectilinear.
True
4. The chord is a line segment.
Answer: A chord is a line segment.
True
5. The arc is a line segment.
Answer: Arc is a line segment.
False
6. There are a finite number of chords of the same length in a circle.
Answer: A circle contains an infinite number of equal chords.
False
7. One and only one circle can be drawn by taking a fixed point as its center.
Answer: Only one circle can be drawn with a center.
False
8. The lengths of the radii of two congruent circles are equal.
Answer: The lengths of the radius of two congruent circles are equal.
True
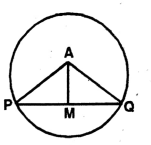
Question 1. I draw a chord PQ of the circle with the Centre, which is not a diameter. I draw a perpendicular on from . I prove with reason that MQ:
Solution: PQ is a chord of a circular with Centre A. AM is the perpendicular from A to PQ
To prove, PM = MQ Join A, P and A, Q.
Proof: In two right angled triangles APM & AQM,
Hypotenuse AP = Hypotenuse AQ [Radii of same circle] AM common.
∴ ΔAPM = ΔAQM (R.H.S)
∴ PM = MQ (Corresponding sides). Proved.
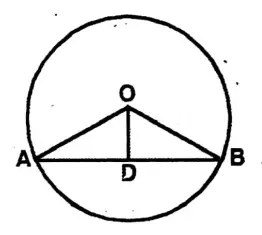
Question 2. I prove the theorem-33 by the proof of congruency of an OBD with the help of the S-A-S axiom of congruency.
Solution: In ΔOAD & ΔOBD
OA = OB (radii of same circle)
∠OAD = ∠OBD (Corresponding angle)
& AD = DB [∵ D is the mid point of AB]
∴ ΔOAD = ΔOBD
∴ ∠ODA = ∠ODB (Corresponding angle)
the adjacent angles formed by OD standing on AB are equal.
∴ OD is perpendicular on AB.
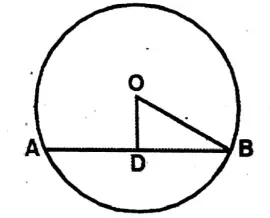
Question 3. The perpendicular distance of a chord from the center of a circle, having a radius of is in length. Let us write by calculating the length of its chord.
Solution: Here OB = 17 cm, OD = 8 cm.
∴ B^2=17^2-8^2=289-64=225
∴ BD = √225 = 15 cm
∴ Chord AB = 2 x 15 cm = 30 cm.
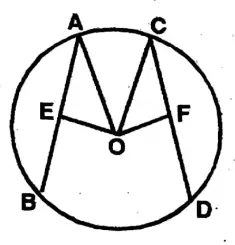
Question 4. I prove with the reason that two equal chords of any circle are equidistant from its centre.
Solution: To prove that two chords of a circle equidistance from the centre are equal.
And OE ⊥ AB, & OF ⊥ CD OE = OF
To prove, AB = CD.
Proof: In two right angled ΔAOE & ΔCOF,
hypotenuse OA = OC (radii of same circle)
OE = OF. (Given)
∴ ΔAOE = ΔCOF
∴ AE = CF (Corresponding sides)
∴ 2 x AE = 2 x CF
∴ AB = CD Proved.
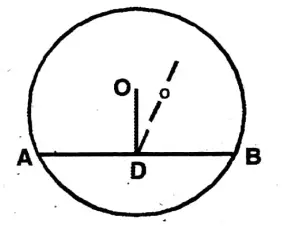
Question 5. Let us prove that the perpendicular bisector of a chord of a circle passes through its centre.
Solution: The prove that the perpendicular of any chord is passing through the centre of the circle.
Let O is the centre and AB is a chord of the circle.
OD ⊥ AB, if possible, let the perpendicular bisect meets at O1.
i.e., OD & OD1 both are perpendicular on AB; it will be possible it OD0 and OD1 coincide with each other.
∴ The perpendicular bisector of the chord is passing through the centre.
Question 6. Let us prove that a straight line cannot intersect a circle at more than two points.
Solution: To prove that a straight line cannot cut a circle at not more than two points.
If possible let the straight line cuts two circles with centre O, at A, B & C points.
Draw the perpendicular on OD from the centre O.
∴ AD = DB & AD = DC.
∴ DB = DC; It will be possible if points B coincide with point C.
∴ A straight line can not cut a circle at more than two points.