WBBSE Solutions For Class 10 Maths Chapter 3 Theorems Related To Circle Exercise 3.2 Solutions
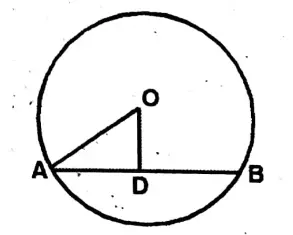
Question 1. The length of a radius of a circle with its centre O is 5cm and the length of its chord AB is 8cm. Let us write by calculating the distance of chord AB from the centre O.
Solution: Centre O, chord AB = 8 cm.
Radius = OA = 5 cm. AD = 4 cm.
\(\mathrm{OD}^2=\mathrm{OA}^2-\mathrm{AD}^2\)= (5)^2-(4)^2=25-16
\(\mathrm{OD}^2=9\)∴ OD = 3 cm.
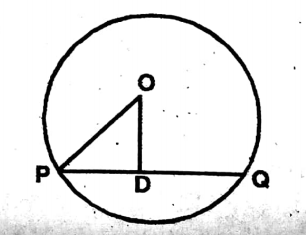
Question 2. The length the diameter of a circle with its centre at O is 26cm. The distance of the chord PQ from point O is 5. Let us write by calculating the length of the chord PQ.
Solution: Diameter = 26 cm
∴ Radius = 13 cm
∴ OP = 13 cm
OD = 5 cm.
\(P D^2=O P^2-O D^2\)= \(13^2-5^2=169-25=144\)

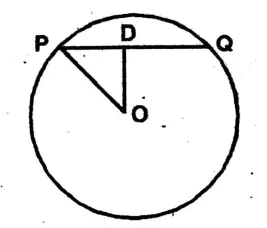
Question 3. The length of a chord PQ of a circle with its centre O is 4cm and the distance of PQ from the point O is 2.1 cm. Let us write by calculating, the length of its diameter
Solution: Centre O;
chord PQ = 4 cm;
OD = 2.1 cm.
\(\mathrm{PO}^2=\mathrm{OD}^2+\mathrm{PD}^2\)= \((2.1)^2+(2)^2=4.41+4=8.41\)
\(\mathrm{PO}=\sqrt{8.41}=2.9\)∴ Radius = 2.9 cm;
Diameter = 2 x 2.9 cm
= 5.8 cm.
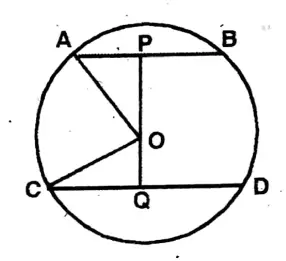
Question 4. The lengths of two chords of a circle with its centre at O are 6CM and 8CM. If the distance of the smaller chord from the centre is 4CM, then let us write by calculating, the distance of another chord from the centre.
Solution: Centre O.
Larger chord CD = 8 cm.
Small chord AB = 6 cm
OP = 4 cm; AP = 3 cm
∴ In △AOP
\(\mathrm{OA}^2=\mathrm{OP}^2+\mathrm{AP}^2\)= \(4^2+3^2\)
= 16 + 9
= 25
OA = √25
= 5 cm.
∴ OC = 5 cm,
\(\mathrm{CQ}=\frac{1}{2} \mathrm{CD}=\frac{1}{2} \times 8 \mathrm{~cm}=4 \mathrm{~cm}\) \(\mathrm{OQ}^2=\mathrm{OC}^2-\mathrm{CQ}^2=5^2-4^2=25-16=9\)OQ = √9 = 3 cm.
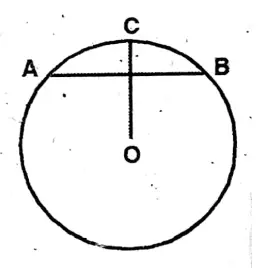
Question 5. If the length of a chord of a circle is 48CM and the distance of it from the centre is 7CM, then let us write by calculating the length of the radius of the circle.
Solution: Centre O; AB = AD = 48 cm, OE = 7 cm.
\(\mathrm{OA}^2=\mathrm{AE}^2+\mathrm{OE}^2(24)^2+(7)^2\)= 576 + 4 = 625
∴ OA = √625 = 25
∴ OC = 25 cm; OF = 20 cm.
\(\mathrm{CF}^2=\mathrm{OC}^2-\mathrm{OF}^2=25^2-20^2=625-400=225\)CF = √225 = 15 cm.
CD = 2 x CF = 2 x 15 = 30 cm.
Length of the 2nd chord = 30 cm.
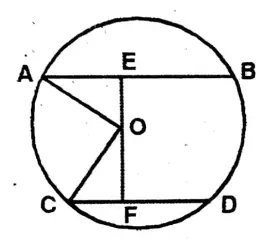
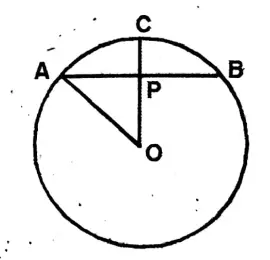
Question 6. In the circle of the adjoining figure with its centre at O, OP⊥AB; if AB = 6CM and PC = 2CM, then let us write by calculating the length of the radius of the circle.
Solution: Centre of the circle O.
Chord AB = 6 cm, AP = 3 cm, PC = 2 cm.
Let Radius OA = OC = r cm.
OP = OC – PC
= (r – 2)cm.
\(\mathrm{OA}^2=\mathrm{OP}^2+\mathrm{AP}^2\) \(r^2=(r-2)^2+3^2\) \(r^2=r^2-4 r+4+9\)4r = 13.
∴ r = \(\frac{13}{4}\) cm.
= 3.25 cm.
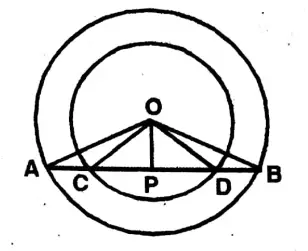
Question 7. A straight line intersects one of the two concentric circles at points A and B and the other at points C and D. I prove with the reason that AC=DB.
Solution: A straight line AB cuts two concentric circles with centre O at A & B and C & D points.
To prove, AC = BD.
As OP is the perpendicular on the chord AB.
∴ AP = BP
Again, OP is the perpendicular on the chord CD.
∴ CP = DP
∴ AP – CP = BP – DP
Or, AC = BD (Proved)
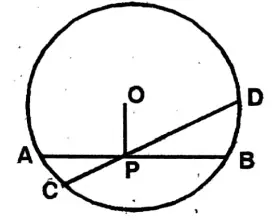
Question 8. I prove that the two intersecting chords of any circle cannot bisect each other unless both of them are diameters of the circle.
Solution: Let O is centre of the circle. Two chords AB & CD interest each other at P, such that the point P is the midpoint of AB.
To prove: P is not the midpoint of CD. Join O, P.
Proof: As P is the midpoint by AB.
∴ OP ⊥ AB
Again, chord AB & CD passing through P. It is not possible that AB & CD both are perpendicular on OP at P.
As AB is perpendicular on OP.
∴ CD is not the perpendicular on OP.
Again, the straight line joining the center and midpoint of the chord, is the perpendicular on the chord.
∴ P is not the midpoint of the chord CD.
If the both straight lines be the diameter, then they will bisect each other.
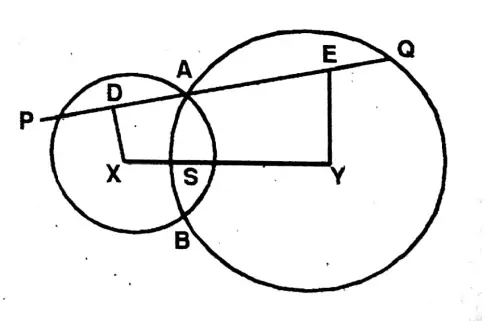
Question 9. The two circles with centres X and Y intersect each other at points A and B. A is joined with the mid-point ‘ S ‘ of XY and the perpendicular on SA through the point A is drawn which intersects the two circles at the points P and Q. Let us prove that PA = AQ.
Solution: Two circles with centres X & Y intersect each other at A and B. S is the mid joint of the line joining X & Y. Join AS The perpendicular on AS cut the circles at P & Q.
To Prove: AP = AQ.
Construction: From two centres X & Y, two perpendiculars drawn on PQ are XD & YE.
Proof: As three straight lines XD, SA & YE are each perpendicular on PQ.
∴ XD ∥ SA ∥ YE
As S is the midpoint of XY.
∴ SX = SY
As three parallel straight lines XD, SA & YE cut the straight line XY in two equal parts, then the lines XD, A, YE cut the other straight PQ into two equal parts.
i.e., DA = AE [As the straight line XD from Y will perpendicular on chord PA]
∴ DA = \(\frac{1}{2}\)AP
Similarly, YE ⊥ AW,AE = \(\frac{1}{2}\)AQ
As DA = AE
∴ \(\frac{1}{2}\)AP = \(\frac{1}{2}\)AQ
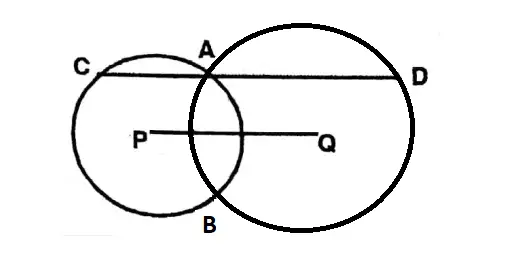
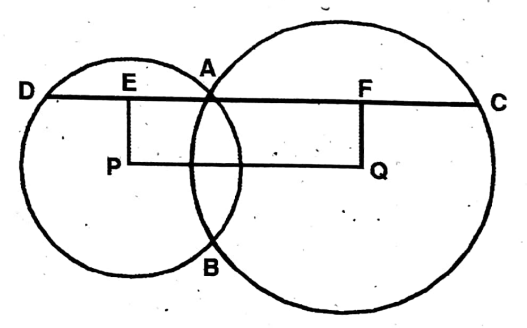
Question 10. The centres of the two circles are P and Q; they intersect at points A and B. The straight line parallel to the line segment PQ through point A intersects the two circles at points C and D.1 prove that CD = 2PQ.
Solution: From the centres P & Q two perpendiculars PE & QF are drawn on CD.
QF bisects AD; AF = \(\frac{1}{2}\)AD.
Again, PE bisects AC; AE = \(\frac{1}{2}\)AC
EF = AF + AE
= \(\frac{1}{2} \mathrm{AD}+\frac{1}{2} \mathrm{AC}\)
EF = \(/frac{1}{2}\)CD
Again, PQ = EF
∴ PQ = \(\frac{1}{2}\)CD
∴ CD = 2PQ (Proved).
Question 11. The two chords AB and AC of a circle are equal. I prove that the bisector of ∠BAC passes through the centre.
Solution: AB & AC are two equal chords of the circle with centre O.
Join OA & OB
In △AOC & △AOB,
1. OB = OC (Radii of same circle)
2. AO Common
3. AB = AC (Given)
∴ \(\triangle \mathrm{AOC} \cong \triangle \mathrm{AOB}\)
∴ ∠OAV = ∠OAB
∴ OA is the bisector of ∠BAC.
∴ Bisector of ∠BAC, is passing through centre (A).
Question 12. I prove that, among two chords of a circle, the length of the chord nearer to the centre is greater than the length of the other.
Solution: AB & CD are two chords of the circle with centre O.
Their distances from the centre are OP & OQ. OP ∠ OQ.
To prove AB > CD Join OB & OD.
As P is the midpoint of AB
∴ PB = \(\frac{1}{2}\)AB and Q is the midpoint of CD.
∴QD = \(\frac{1}{2}\)CD
In \(\triangle \mathrm{OPB}, \mathrm{OB}=\sqrt{\mathrm{PB}^2+\mathrm{OP}^2}\)
In \(\triangle O Q D, O D=\sqrt{O Q^2+Q D^2}\)
∴ \(\sqrt{\mathrm{PB}^2+\mathrm{OP}^2}=\sqrt{\mathrm{OQ}^2+\mathrm{QD}^2}\)
\(\mathrm{PB}^2+\mathrm{OP}^2=\mathrm{OQ}^2+\mathrm{QD}^2\)As OP < OQ
∴ OB > QD
\(\frac{1}{2} \mathrm{AB}>\frac{1}{2} \mathrm{CD}\)
Question 13. Let us write by proving the chord with the least length through any point in a circle.
Solution: P is a point inside the circle.
Chord AB passing through P will be smaller if the point P will be the midpoint of AB.
If P in the mid point of AB
∴ OP ⊥ AB
as perpendicular distance is the shortest distance.
∴ AB is smallest (Proved).
Chapter 3 Theorems Related To Circle Exercise 3.2 Multiple Choice Questions
Question 1. The lengths of two chords of a circle with centre O are equal. If ∠AOB = 60°, then the value of ∠COD is
1. 40°
2. 30°
3. 60°
4. 90°
Answer:
The lengths of two chords of a circle with centre O are equal. If ∠AOB = 60°,
AB & CD are two equal chords of the circle with O if LAOB = 60°; then /COD = 60°———-(3)
Question 2. The length of the radius of a circle is 13 cm and the length of a chord of a circle is 10 cm, the distance of the chord from the centre of the circle is
1. 12.5 cm
2. 12 cm
3. √69 cm
4. 24 cm
Answer:
The length of the radius of a circle is 13 cm and the length of a chord of a circle is 10 cm
Radius = 13 cm. length of chord = 10 cm, Distance from the centre = √132 -52
= √169-25
= √144
=12-——(2)
The distance of the chord from the centre of the circle is 12
Question 3. AB and CD are two equal chords of a circle with its centre O. If the distance of the chord AB from the point O is 4 cm then the distance of the chord from the centre O of the circle is
1. 2 cm
2. 4 cm
3. 6 cm
4. 8 cm
Answer:
AB and CD are two equal chords of a circle with its centre O. If the distance of the chord AB from the point O is 4 cm
AB & CD are two equal chords.
If the distance of AB from the centre O = 4 cm.
then the distance of CD from the centre O 4 cm. ——- -(2)
Question 4. The length of each of the two parallel chords is 16 cm. If the length of the radius of the circle is 10 cm., then the distance between two chords is
1. 12 cm.
2. 16 cm.
3. 20 cm.
4. 5 cm.
Answer:
The length of each of the two parallel chords is 16 cm. If the length of the radius of the circle is 10 cm
Two parallel chords of equal length 16 cm.
Length of the radius = 10 cm.
Distance between them = √102-82 + √102-826+6 12 cm. ————(1)
Question 5. The centre of two concentric circles is O; a straight line intersects a circle at points A and B and the other circle at the point C and D. If AC = 5 cm, then the length of BD is
1. 2.5 cm
2. 5 cm
3. 10 cm
4. None of these
Answer:
The centre of two concentric circles is O; a straight line intersects a circle at points A and B and the other circle at the point C and D. If AC = 5 cm
When a straight line cuts two concentric circles at A & B and C & D points, AC = BD.
BD 5 cm.———–(2)
Chapter 3 Theorems Related To Circle Exercise 3.2 True or False
1. Only one circle can be drawn through three collinear points.
Answer: False
2. The two circles ABCDA and ABCEA are the same circle.
Answer: True
3. If two circles AB and AC of a circle with its centre O are situated on opposite sides of the radius OA, then LOAB = LOAC.
Answer: False
Chapter 3 Theorems Related To Circle Exercise 3.2 Fill In The Blanks
Question 1. If the ratio of two chords PQ and RS of a circle with its centre O is 1: 1, then, LPOQ: LROS =—————–
Answer: LPOQ: LROS = 1:1.
Question 2. The perpendicular bisector of any chord of a circle is—————–
Answer: Passing through the centre.
Chapter 3 Theorems Related To Circle Exercise 3.2 Short Answers
Question 1. Two equal circles of radius 10 intersect each other and the length of their common chord is 12 cm. Let us determine the distance between the two centres of the two circles.
Solution: CD = 12 cm.
∴ CO = \frac{12}{2} = 6 cm.
AO = \sqrt{10^2-6^2}=\sqrt{64}=8
AB = 2 x 8 = 16 cm.
∴ Distance between two centres = 16 cm.
Question 2. AB and AC are two equal chords of a circle having a radius of 5 cm. The centre of the circle is situated at the outside of the triangle ABC. IF AB = AC = 6 cm, then let us calculate the length of the chord BC.
Solution: AB = AC = 6 cm.
OA = 5 cm.
Let AP = a cm. PO = b cm.
OA = a + b = 5 cm.
\(\mathrm{BP}=\mathrm{CP}=\mathrm{na}^2+\mathrm{n}^2\)= \(6^2 \& b^2+n^2\)
= \(5^2 a^2+n^2-b^2-n^2\)
= \(6^2-5^2\)
= 36 – 25
= \(11 a^2-b^2\)
= 11.(a – b) x (a + b)
= 11
∴ (a – b) x 5 = 11a – b
= \(\frac{11}{5} \mathrm{a}=\frac{1}{2}\left(\frac{11}{2}+5\right)=\frac{18}{5}\)
∴ \(n=\sqrt{6^2-\left(\frac{18}{5}\right)^2}=\sqrt{36-\frac{324}{25}}=\sqrt{\frac{576}{25}}=\frac{24}{5}\)
∴ \(\mathrm{BC}=2 \mathrm{n}=2 \times \frac{24}{5}=9.6 \mathrm{~cm}\)
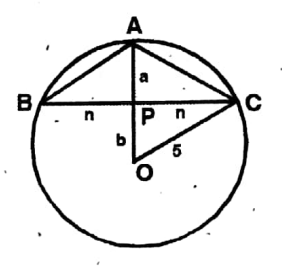
Question 3. The length of two chords AB and CD of a circle with its centre O are equal. If LAOB = 60° and CD = 6 cm, then let us calculate the length of the radius of the circle. Ans. AB = CD = 6 cm.
Solution: AB = CD = 6 cm.
∠AOB = 60°
∴ △AOB is an equilateral triangle.
OA = OB = 6 cm.
∴ Radius = 6 cm.
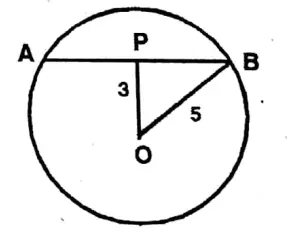
Question 4. P is any point in a circle with its centre O. If the length of the radius is 5 cm and OP = 3 cm, then let us determine the least length of the chord passing through the point P.
Solution: BP = \(\sqrt{5^2-3^2}\)
= \(\sqrt{25-9}=\sqrt{16}=4\)
AB = 2 x BP = 2 x 4 = 8 cm.
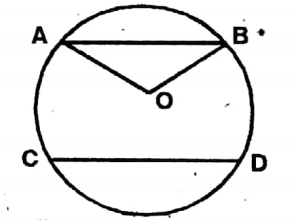
Question 5. The two circles with their centres at P and Q intersect each other at points A and B. Through point A, a straight line parallel to PQ intersects the two circles at points C and D respectively. If PQ = 5 cm, then let us determine the length of the CD.
Solution: PQ = 5cm, CD = ?
CD = 2PQ = 2 x 5 cm
= 10 cm