WBBSE Solutions For Class 10 Maths Chapter 4 Rectangular Parallelopiped or Cuboid Exercise 4.2

WBBSE Solutions For Class 10 Maths Chapter 4 Rectangular Parallelopiped or Cuboid Exercise 4.2

Question 1. Let us write the names of 4 cuboids and 4 cube-shaped solid things in our environment.

1. Name of 4 rectangular parallelopipeds:
Brick;
Matchbox;
Mathematics book;
Geometry box.

2. Name of 4 cubes:
Dice of ludo;
Ice cube;
Rubix cube;
Square suitcase.

Read and Learn More WBBSE Solutions For Class 10 Maths

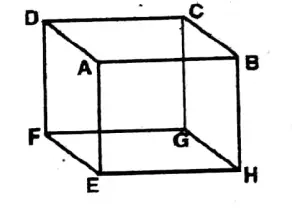
Question 2. Let us write the names of surfaces, edges, and vertices of the adjoining cuboidal.

Name of the surfaces:
ABCD;
EFGH;
ADEF;
BCGH;
ABEH;
CDFG.

Name of the edges:
AB,
BC,
CD,
DA,
EF,
FG,
EH,
GH,
AE,
BH,
CG & F
G.

Vertexes are:
A,
B,
C,
D,
E,
F,
G
& H.

Question 3. The length, breadth, and height of a cuboidal room are 5 m, 4 m, and 3 m respectively. Let us write the length of the longest rod which can be kept in that room.

Solution: Length of the rod = Diagonal of the room

= \(\sqrt{1^2+b^2+h^2}\)

= \(\sqrt{5^2+4^2+3^2}=\sqrt{25+16+9}=\sqrt{50}=5 \sqrt{2} \mathrm{~m}\)

Question 4. The area of one surface of a cube is 64 sq.m., let us calculate the volume of the cube.

Solution: Surface area of the cube = 64 sqm.

∴ Length of one side of the cube = √64 = 8 m.

∴ The volume of the cube = ṁ

Question 5. In our Bokultala village, a canal is cut whose breadth is 2 m and depth is 8 d cm. If the total quantity of soil extracted is 240 cubic metres, then let us calculate the total surface area of the cube.

Solution: Let the length of the canal = x m.

Breadth = 2 m.

Depth = 8 d cm. = 0.8 m.

∴ According to the problem,

= x.2.(0.8)

= 240

∴ \(x=\frac{240}{2 \times 0.8}=\frac{240 \times 10}{2 \times 8}=150 \mathrm{~m}\)

 

Question 6. If the length of the diagonal of a cube is 4√3 cm, then let us calculate the total surface area of the cube.

Solution: Diagonal of a cube = 4√ 3 cm.

As diagonal of a cube = √ 3 x side.

Length of one side of the cube

= \(\frac{4 \sqrt{3}}{\sqrt{3}}\)

= 4 cm.

∴ Total surface area of a cube

= \(6 \times(\text { side })^2\)

= \(6 \times(4)^2\)

= 16 x 6 sqcm.

= 96 sqcm.

 

Question 7. The sum of the length of the edges of a cube is 60 cm, let us out the volume of the cube.

Solution: There are 12 edges of a cube & all the edges are equal.

∴ 12 x Length one edge = 60 cm

∴ Length of one edge = \(\frac{60}{12} \mathrm{~cm}=5 \mathrm{~cm}\)

Volume of a cube = (one edge)³ = (5)³ cu.cm = 125 cu.cm.

 

Question 8. If the sum of the areas of 6 surfaces of a cube is 216 sq. cm, then let us calculate the volume of the cube.

Solution: Total area of 6 surfaces of cube = 6 x (side)²

∴ \(6 \times(\text { side })^2=216 \text { sqcm }\)

∴ \((\text { Side })^2=\frac{216}{6}=36 \mathrm{sqcm} .\)

∴ Length of one side = √36 = 6 cm

∴ Volume of a cube = (side)³ = (6 cm)³ = 216 cu.cm.

 

Question 9. The volume of a rectangular parallelopiped is 432 sq. cm. If it is converted into two cubes of equal volumes, then let us calculate the length of each edge of each cube.

Solution: Volume of a rectangular parallelopiped is 432 cu.cm.

If it is bisected into two equal cubes

∴ Volume of each cube = \(\frac{432}{2}\)

= 216 cu.cm.

(Length of each edge)³ = 216

Length of each edge = \(\sqrt[3]{216}\)

= 6 cm.

 

Question 10. Each side of a cube is decreased by 50%. Let us calculate the ratio of the volumes of the original cube and the changed cube.

Solution: Let one side of a cube = x cm.

∴ Its volume = x³ cu.cm.

If the length is reduced 50% then the new length of the cube = \(\frac{x}{2}\) cm.

∴ Volume of the new cube = \(\left(\frac{x}{2} \mathrm{~cm}\right)^3=\frac{x^3}{8}\)

∴ Ratio of volume of the original cube & volume of new cube

= \(x^3: \frac{x^3}{8}\)

= \(1: \frac{1}{8}\)

= 8 : 1

 

Question 11. If the ratio of length, breadth and height of a cuboidal box is 3: 2:1 and its volume is 384 cc then let us calculate the total surface area of the box.

Solution: Let the length, breadth & height of the rectangular box are 3x cm, 2x cm & : cm respectively.

According to the problem,

3x, 2x, x = 384

or, 6x³ = 384

\(x^3=\frac{384}{6}=64=(4)^3\)

∴ x = 4

Length = 3 x 4 = 12 cm.

Breadth = 2 x 4 = 8 cm.

& Height = 1 x 4 = 4 xm.

Total Area of 6 surfaces of the rectangular parallelopiped

= 2(L x B + L x H + B x H)

= 2(12 x 8 + 12 x 4 + 8 x 4) sqcm.

= 2(96 + 48 + 32) sqcm.

= 2(96 + 48 + 32) sqcm

= 2 x 176 sqcm.

= 352 sqcm.

 

Question 12. The inner length, breadth and height of a box of tea are 7.5 dcm and 5.4 dcm respectively, if the weight of the box filled with tea is 52 kg 350gm, but in an empty state, its weight is 3.75 kg then let us write by calculating, the weight of 1 cubic dcm. tea.

Solution: Inside length = 7.5 dcm.

Breadth = 6 dcm.

& Height = 5.4 dcm.

Inside volume of the box

= (7.5 x 6 x 5.4) cu.dcm.

= 243 cu.dcm.

The weight of tea = (52.350 – 3.750)kg.

= 48.600 kg.

∴ Weight of 243 cu.dcm tea = 48.60 kg.

∴ Weight of 1 cu.dcm tea = \(\frac{48.60}{243} \mathrm{~kg}=0.2 \mathrm{~kg}=200 \mathrm{gm}\)

∴ Weight of 1 cu dcm tea = 200gm.

 

Question 13. The length, breadth and weight of a brass plate with a squared base are x cm, 1 mm and 4725 gm respectively, if the weight of 1 cubic dcm of brass is 8.4 gm, then let us write by calculating the value of x.

Solution: Length of the square plate = xcm.

Breadth of the square plate = x cm

Height of the square plate = 1 mm = 0.1 cm.

Volume of the square plate = \(0.1 \mathrm{x}^2 \mathrm{cu} . \mathrm{cm}\)

Wt. of 1 cu.cm brass plate = 8.4 gm.

Wt. of \(0.1 \mathrm{x}^2 \mathrm{cu} . \mathrm{cm}\) brass plate = \(0.1 x^2 \times 8.4 \mathrm{gm}\)

According to the problem, \(0.1 \mathrm{x}^2 \times 8.4=4725\)

∴ \(x^2=\frac{4725}{0.1 \times 8.4}=225 \times 25\)

∴ \(x=\sqrt{225 \times 25}\)

= 15 x 5

= 75 cm.

∴ Value of x = 75 cm.

 

Question 14. The height of Chandamri Road is to be raised. So, 30 cuboidal holes with equal depth and of equal measure are dug out on both sides of the road and with this soil, my road is elevated. If the length and breadth of each hole are 14 m and 8 m respectively and if the total quantity of soil required to make the road is 2520 cubic metres men let us calculate the depth of each hole.

Solution: Let the depth of each hole = x m.

Volume of each hole = 14 x 8 x x cum.

Volume of 30 holes = 30 x 14 x 8 x x cum.

According to the problem,

30 x 14 x 8 x x = 2520

∴ \(x=\frac{2520}{30 \times 14 \times 8}=\frac{6}{8}=\frac{3}{4} \mathrm{~m}\)

∴ Depth of each hole

= \(\frac{3}{4} m\)

= 0.75 m.

 

Question 15. If 64 water-filled buckets of equal measure are taken out from a cubical water-filled tank, then 1/3rd of the water remains in the tank. If the length of one edge of the tank is 1.2 m, then let us calculate and write the quantity of water that can be held in each bucket.

Solution: Length of each side of the tank = 1.2m

Volume of the tank

= \((1.2 \mathrm{~m})^3 \mathrm{~m}^3\)

= 1.728 m³

= 1728 cu.dcm.

= 1728 litre.

In 64 buckets water contained

= \(\left(1-\frac{1}{3}\right)\)

= \(\frac{2}{3}\) part of the tank

= \(\frac{2}{3}\) x 1728 litre

= 2 x 576 litre.

∴ 1 Bucket contains = \(\frac{2 \times 576}{64}\)

= 18 litres.

Question 16. If the length, breadth and height of one packet of one gross matchbox are 2.8 dcm and 0.9 dcm respectively, then let us calculate the volume of one match box [one gross 12 dozen]. But if the length and breadth of one matchbox be 5 cm and 3.5 cm, then let us calculate its height of it.

Solution: Volume of 1 gross (12 x 12)

match boxes = (2.8 x 1.5 x 0.9) cu.acm.

Volume of 1 match box = \(\frac{2.8 \times 1.5 \times 0.9}{12 \times 12}\) cu.dcm.

= \(\frac{3.780}{12 \times 12}\) cu.dcm

= 0.02625 cu.dcm

= 26.25 cu.cm.

Let the height of a match box = hcm.

∴ Volume = 5 x 3.5 x h cu.cm.

∴ 17.5 h = 26.25

∴ \(\mathrm{h}=\frac{26.25}{17.5}=1.5 \mathrm{~cm}\)

∴ Height of each match box = 1.5 cm.

Question 17. Half of a cuboidal water tank with a length of 2.1 m and breadth of 1.5 m is filled with water. If 630 litres of water is poured more into the tank, then let us calculate and write the depth that will be increased.

Solution: Length of the tank = 2.1m = 21dcm.

Breadth of the tank = 1.5 m = 15 dcm

Let the height of increased water = x dcm.

∴ According to the problem,

21 x 15 x x = 630

∴ \(x=\frac{630}{21 \times 15}=2\)

∴ Height of the water level increased by 2 dcm.

Question 18. The length and breadth of a rectangular field of the village are 20 m and 15 m respectively. For the construction of pillars in the 4 corners of that field 4 cubic holes having lengths of 4 m are dug out and the soils removed are dispersed on the remaining land. Let us calculate and write the height of the surfaces of the field that is increased by.

Solution: Area of the field

= 20 m x 15 m

= 300 sqm.

Area of the land for 4 pillars

= 4 x (4)² sqm.

= 64 sqm.

∴ Remaining part of the land

= (300 – 64) sqm.

= 236 sqm.

Volume of earth removed

= 4 x (4)³ Cum

c = 256 Cum.

Let increased height of the remaining field x m.

∴ 236 x x = 256

\(x=\frac{256}{236}=\frac{64}{59}=1 \frac{5}{59} \mathrm{~m}\)

 

Question 19. For elevating 6.5 DCM of low land with a length of 48 m and breadth of 31.5 m, it is decided that the soil will be collected by scooping a hole in a nearby land with a length of 27 m and breadth of 18.2 m, let us calculate the depth of the hole in metre.

Solution: Let the depth of the hole – xm.

Volume of earth removed from the hole = 27 x 18.2 x x cum.

According to the problem,

27 x 18.2 x x = 48 x 31.5 x 0.65

∴ \(\mathrm{x}=\frac{48 \times 31.5 \times 0.65}{27 \times 18.2} \mathrm{~m}\)

= \(\frac{48 \times 315 \times 65}{27 \times 182 \times 100}=2 \mathrm{~m}\)

∴ Depth of the hole = 2 m.

 

Question 20. There were 800 lit, 725 lit and 575 lit kerosene oil in three kerosene oil drums of the house. The oil of these three drums is poured into a cuboidal pot and for this, the depth of oil in drums becomes 7 dams. If the ratio of the length and breadth of the cuboidal pot is 4: 3, then let us write by calculating the length and breadth of the pot. If the depth of the cuboidal pot would be 5 dcm, then let us calculate whether 1620 lit oil can be kept or not in that pot.

Solution: Let the length & the breadth of the rectangular tank are 4x d cm & 3x dcm

Total volume of soil = (800 + 725 + 575) litre.

∴ Volume of the tank = (4 x x 3x x 7) cu.dcm.

According to the problem,

4x x 3x x 7 = 2100

Or 84 x^2=2100

∴  \(x^2=\frac{2100}{84}=25\)

∴ x = √ 25 = 5

∴ Length & breadth of the tank = (4 x 5)d cm and (3 x 5)d cm = 20 dcm & 15 dcm.

Question 21. The daily requirements of water for three families in our three-story flat are 1200 lit, 1050 lit and 950 lit respectively. After fulfilling these requirements in order to put up a tank again and to deposit to store 25% of the required water, only land having a length of 2.5 m and breadth of 1.6 m has been produced. Let us calculate the depth of the tank in metres that should be made. If the breadth of the land would be more by 4 dcm, then let us calculate the depth of the tank to be made.

Solution: Total volume of water required for 3 families = (1200 + 1050 + 950)

litre = 3200 litre.

Now to keep 25% of more water, i.e., 3200 \times \(\frac{25}{100}=800 litre\).

Total volume of water = (3200 + 800) = 4000 litre.

Length of the tank = 2.5 m = 25 dcm.

Breadth of the tank = 1.6m = 16 dcm.

Let the height of the tank = x dcm.

∴ 25 x 16 x x = 4000

∴ \(x=\frac{4000}{25 \times 16}=10 \mathrm{dcm} .=1 \mathrm{~m}\)

Question 22. The weight of a wooden box made of wooden planks with a thickness of 5 cm along with its covering is 115.5 kg. But the weight of the box filled with rice is 880.5 kg. The length and breadth of the inner side of the box are 12 dcm and 8.5 dcm respectively and the weight of 1 cubic dcm rice is 1.5 kg. Let us write the inner height of the box after calculation. Let us calculate the total expenditure of colour the outside of the box if the rate is Rs. 1.50 per sq. dcm.

Solution: Weight of rice inside the box = (880.5 – 115.5) kg.

= 765 kg.

Volume of the box = \(\frac{765}{1.5}\) = 510 cu.dcm.

Let the height of the box = h dcm.

According to the problem,

12 x 8.5 x h = 510

\(\mathrm{h}=\frac{510}{12 \times 8.5}=5 \mathrm{dcm}\)

Outside length of the box = (12 + 2 x 0.5) = 13 dcm.

Outside breadth of the box = (8.5 + 2 x 0.5) = 9.5 dcm.

Outside height of the box = (5 + 2 x 0.5) = 6 dcm.

Total outside surface area o fthe box = 2(13 x 9.5 + 13 x 6 + 9.5 x 6) sq.dcm.

= 2(123.5 + 78 + 57) = 2 x (258.5) = 517 sq.dcm.

∴ 517 x Rs. 1.50 = Rs. 775.50.

Question 23. The depth of a cuboidal pond with a length of 20 m and breadth of 18.5 m is 3.2 m, let us write by calculating the time required to irrigate the whole water of the pond with a pump having the capacity to irrigate 160-kilo lit water per hour. If that quantity of water is poured on a paddy field with a ridge having a length of 59.2 m and a breadth of 40 m, then what is the depth of water in that land – let us write by calculating it. [1 cubic metre = 1 kilo litre]

Solution: Volume of the water in the rectangular tank = (20 x 18.5 x 3.2) cum.

= 1184 cum.

= 1184 Kilolitre.

Time required to remove the water from the tank by pump

= \(\frac{1184}{160}\)

= \(\frac{37}{5}\) hr

= 7hr24 m.

2nd part:

Let the height of water in the paddy field = hm.

Volume of water in the paddy field will be 59.2m x 40 m . h m. = 2368 h cum.

∴ 2368h = 1184

∴ \(\mathrm{h}=\frac{1184}{2368}=0.5 \mathrm{~m}\)

∴ Height of water level = 0.5 m.

Chapter 4 Theorems Related To Circle Exercise 4.2 Multiple-Choice Questions

Question 1. The inner volume of a cuboidal box is 440 cc. and the area of the inner base is 88 sq. cm, the inner height of the box is

1. 4 cm
2. 5 cm
3. 3 cm
4. 6 cm

Answer.

Given

The inner volume of the rectangular box = 440 cu. cm.

& inner area of the bottom of the box = 88 sqm.

Height of the box =440/88=5cm————–(b)

Question 2. The length, breadth and height of a cuboidal hole are 40 m, 12 m and 16 m respectively. The number of planks having a height of 5 m breadth of 4 m and thickness of 2 m, can be kept in that hole is

1. 190
2. 192
3. 184
4. 180

Answer: The length, breadth & height of a rectangular hole are 40m, 12 m & 26 m respectively

volume = (40 x 12 x 16)m³.

And the length, breadth & thickness of a rectangular wooden plank are 5m, 4m & 2m respectively.

∴ Its volume = (5 x 4 x 2)m³.

∴ No. of planks = \(\frac{40 \times 12 \times 16}{5 \times 4 \times 2}=12 \times 16=192\)         …(2)

Question 3. The surface area of a cube is 256 sq.m, and the volume of the cube is

1. 64 cubic metre
2. 216 cubic metre
3. 256 cubic metre
4. 512 cubic metre

[Hints: The number of surfaces is 6]

Answer: Side faces of a cube = 256 sqm

∴ Area of one surface = \(\frac{256}{4}=64 \text { sqm. }\)

∴ Each side of the cube = √64 = 8 m.

∴ Volume of the cube = (8)³ = 512 m³       …(4)

Question 4. The ratio of the volumes of the two cubes is 1: 27, and the ratio of the total surface areas of the two cubes is

1. 1:3
2. 1:8
3. 1:9
4. 1: 18

Answer: As the ratio of volume of two cubes are 1 : 27.

∴ The ratio of each side of the cubes

= 3√1 : 3√27 = 1:3.

The ratio of total surface areas of the two cubes

= 6(1)² : 6(3)² = 1² : 3² = 1 : 9

Question 5. If the total surface area of a cube is s sq. unit and the length of the diagonal is d unit, then the relation between s and d is

1. s = 6d²

2. 3s = 7d

3. S³ = d2

4. d² = s/2

Answer: Total surface area of a cube = s sq.unit.

Diagonal of a cube = d unit.

Let one side of cube x unit.

∴ Total surface area (s) = 6x² sq unit.

Diagonal (d) = √3x unit

∴ d = 2d²

∴ \(\frac{s}{2}\) = d²    —-(4)

 

Chapter 4 Theorems Related To Circle Exercise 4.2 True or False

1. If the length of each edge of a cube is twice of that 1st cube then the volume of this cube is 4 times more than that of the 1st cube.

False

2. In the rainy season, the height of rainfall in 2 hectares of land is 5 cm, and the volume of rainwater is 1000 cubic metres.

True

Chapter 4 Theorems Related To Circle Exercise 4.2 Fill In The Blanks.

1.  The number of diagonals of a cuboid is No. of diagonals = 4

2. The length of the diagonal on the surface of a cube =  √2  x the length of one edge.