WBBSE Solutions For Class 10 Maths Chapter 5 Ration And Proportion Exercise 5.1
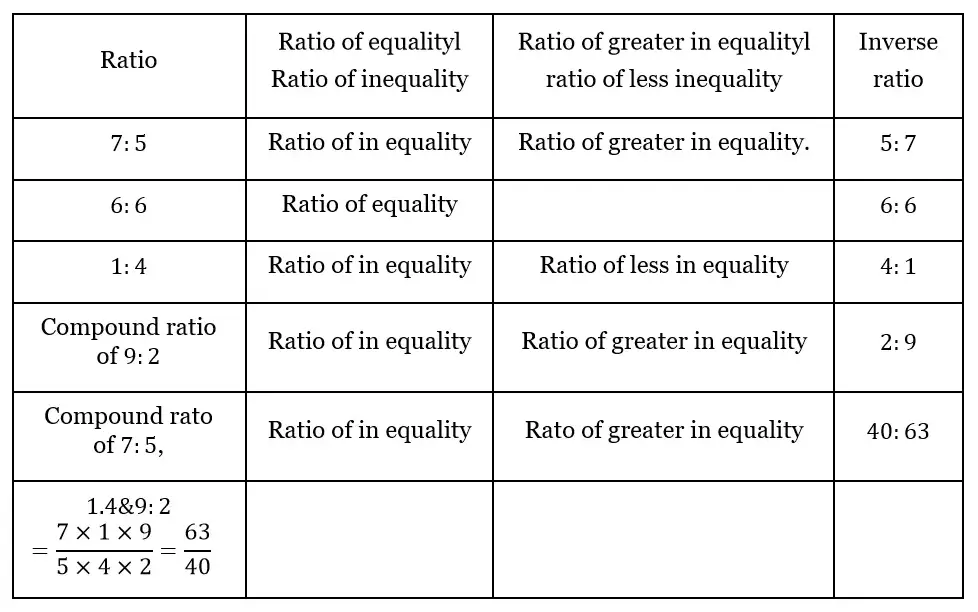
Question 1. Let us see the ratios given below and let us write in the blank places.
Solution:
Question 2. Let us write the inverse ratio of the lowest form of x2yp: xy2p
Read and Learn More WBBSE Solutions For Class 10 Maths
Solution: x^2 y p: x y^2 p
= \(\frac{x}{y}\)
= x : y
∴ Inverse ratio of the lowest form of \(x^2 y p: x^2\) p is y : x.
Question 3. If the ratio of two numbers is 2: 3 and their H.C.F is 7, let us write two numbers.
Solution: Numbers are (2 x 7) = 14 and (3 x 7) = 21.
Question 4. Let us write the inverse ratio of the mixed ratio of three ratios p2q: r, qr: p, and r2p: q.
Solution: Compound ratio of \(p^2 q: r, q^2 r: p\)
and \(\mathrm{r}^2 \mathrm{p}: \mathrm{q} \text { is } \mathrm{p}^2 \mathrm{q}^2 \mathrm{r}^2: \mathrm{pqr}: 1\)
∴ the inverse ratio = 1 : pqr.
Question 5. If A: B=3:7 and B: C = 8:5, let us find A: C [Let me do it myself]. Solution: A B = 4:5 and B: C=6:7
Solution: A : B = 4 : 5
And B : C = 6 : 7
∴ \(\frac{\mathrm{A}}{\mathrm{B}} \times \frac{\mathrm{B}}{\mathrm{C}}=\frac{4}{5} \times \frac{6}{7}=\frac{24}{35}\)
∴ A : C = 24 : 35
Question 6. If A: B=5:9 and B: C = 4:5, let us write the value of A: B: C .
Solution: If A : B = 5 : 9
and B : C = 4 : 5,
the value of B in two cases 9 & 4, their LCM = 9 x 4 = 36
A : B = 5 : 9 = 5 x 4 : 9 x 4 = 20 : 36
B : C = 4 : 5 = 4 x 9 : 5 x 9 = 36 : 45
∴ A : B : C = 20 : 36 : 45

Question 7. If x: y = 7:4, let us show that (5x-6y): (3x+11y) 11: 65 .
Solution: x : y = 7 : 4
Let, x = 7p & y = 4p
∴ \(\frac{5 x-6 y}{3 x+11 y}=\frac{5 \times 7 p-6 \times 4 p}{3 \times 7 p+11 \times 4 p}=\frac{35 p-24 p}{21 p+44 p}=\frac{11 p}{65 p}=\frac{11}{65}\)
∴ (5x – 6y) : (3x + 11y) = 11 : 65
Alternative method:
\(\frac{5 x-6 y}{3 x+11 y}=\frac{\frac{5 x-6 y}{y}}{\frac{3 x+11 y}{y}}=\frac{5 \frac{x}{y}-6}{3 \frac{x}{y}+11}=\frac{5 \times \frac{7}{4}-6}{3 \times \frac{7}{4}+11}\)= \(\frac{\frac{35}{4}-6}{\frac{21}{4}+11}=\frac{\frac{35-24}{4}}{\frac{4}{4}}=\frac{11}{65}=11: 65\)
Question 8. If (2x+5y): (5x-7y)= 5: 3, let us find x: y.
Solution: (2x + 5y) : (5x – 7y) = 5:3
or, \(\frac{2 x+5 y}{5 x-7 y}=\frac{5}{3}\)
or, 5(5x – 7y) = 3(2x + 5y)
or, 25x – 35y = 15y + 35y
or, 19x = 50y
or, \(\frac{x}{y}=\frac{50}{19}\)
∴ x : y = 50 : 19
Question 9. If (7x – 5y): (3x+4y) = 7: 11, let us find the value of (5x-3y): (6x +5y).
Solution: (7x – 5y) : (3x + 4y) = 7 : 11
or, \frac{7 x-5 y}{3 x+4 y}=\frac{7}{11}
or, 11(7x – 5y) = 7(3x + 4y)
or, 77x – 55y = 21x + 28y
or, 77x – 21x = 55y + 28y
or, 56x = 83y
or, \frac{x}{y}=\frac{83}{56}
or, x : y = 83 : 56
∴ Let x = 83p & y = 56p
(5x – 3y) : (6x + 5y)
(5x – 3y) : (6x + 5y)
= (5 x 83p – 3 x 56p) : (6 x 83p + 5 x 56p)
= (415p – 168p) : (498p + 280p)
= 247p : 778p
= 247 : 778.
Question 10. Let us write what should be added to each term of the ratio 5: 3 to make the ratio 7: 6.
Solution: Let the required number be x, which should be added to the both terms.
∴ \frac{5+x}{3+x}=\frac{7}{6}
or, 7(3 + x) = 6(5 + x)
or, 21 + 7x = 30 + 6x
or, 7x – 6x = 30 – 21
∴ x = 9
∴ the required number = 9
Question 11. Let us express the following as ratio and let us write by understanding ratio of equality, ratio of leser inequality, ratio of greater inequality in each case :
1. 4 months and 1 year 6 months
Solution: 4 months:
1 year 6 months = 4 months (126) months
= 4 months: 18 months
= 2: 9 The ratio is of lesser inequality.
2. 75 paise and Re. 1 and 25 paise
Solution: 75p & Re. 1 & 25p
= 75p: 125p
=3:5 This ratio is of lesser inequality.
3. 60 cm and 0.6 meter
Solution: 60 cm. & 0.6 m.
= 60 cm: (0.6 x 100)cm 60 cm: 60 cm
= 1:1 This is equality.
4. 1.2 kg and gram.
Solution: 1.2 kg & 60 gm
= 1.2 kg: 60 gm
= (1.2 x 1,000) gm: 60 gm
=1200 gm 60 gm
= 20:1 This ratio is of greater inequality.
Question 12.
1. Let us write the ratio of p kg and q gram.
Solution: p kg & q gram
= (px 1000)gm: q gram
= 1000 p: q
2. Let us write when it is possible to find the ratio of x days and z months.
Solution: It is possible if both quantities are expressed in the same unit.
3. Let us write what type of mixed ratio of a ratio and its inverse ratio.
Solution: It will be equality.
4. Let us find the mixed ratio of a/b: c, b/c: a c/a: b
Solution: The compound ratio of \(\left(\frac{a}{b}: c\right) ;\left(\frac{b}{c}: a\right) \&\left(\frac{c}{a}: b\right)\) is \(\left(\frac{a}{b} \times \frac{b}{c} \times \frac{c}{a}\right):(c \times a \times b)=1: a b c\)
5. Let us write by calculating what ratio x2: yz will form with the mixed ratio xy: z2.
Solution: Let the required ratio = p : q
∴ \(\left(x^2 \cdot p\right):(y z \cdot q)=x y: z^2\)
or, \(\frac{p x^2}{q y z}=\frac{x y}{z^2}\)
∴ \(\frac{p}{q}=\frac{x y \cdot y z}{x^2 \cdot x^2}\)
= \(\frac{y^2}{x z}=y^2: x z\)
6. Let us calculate the compound ratio of inverse ratios of x2: yz/x, y2: zx/y, x2:yx/z
Solution: The inverse ratios of \(\left(x^2: \frac{y z}{x}\right),\left(y^2: \frac{z x}{y}\right) \&\left(z^2: \frac{x y}{z}\right) are \left(\frac{y z}{x}: x^2\right),\left(\frac{z x}{y}: y^2\right) \&\left(\frac{y x}{z}: z^2\right).\)
The required compound ratio is
\(\left(\frac{y z}{x} \times \frac{z x}{y} \times \frac{y x}{z}\right):\left(x^2 \times y^2 \times z^2\right)\)= \(x y z: x^2 y^2 z^2=1: x y z\)
Question 13. Let us find the mixed ratio or compound ratio of the following ratios
1. 4:5, 5:7 and 9: 11
Solution: The compound ratio of (4: 5), (5: 7) & (9: 11) is (4 x 5 x 9): (5 x 7 x 11)= 36: 77
2. (x+y): (xy), (x2 + y2) (x + y)2 and (x2 y2)2: (x4 – y4)
Solution: The compound ratio of
\((x+y):(x-y) ;\left(x^2+y^2\right):(x+y)^2 \&\left(x^2-y^2\right): x^4-y^4\)= \(\frac{(x+y)\left(x^2+y^2\right)\left(x^2-y^2\right)^2}{(x-y)(x+y)^2 \cdot\left(x^4-y^4\right)}\)
= \(\frac{(x+y)\left(x^2+y^2\right)(x+y)^2\left(x^2-y^2\right)^2}{(x-y)(x+y)(x+y)\left(x^2+y^2\right)(x-y)(x+y)}\)
= \(\frac{(x+y)^3(x-y)^2}{(x+y)^3(x-y)^2}=\frac{1}{1}=1: 1\)
Question 14.
1. If A: B 6: 7 and B: C = 8: 7, let us find A: C.
Solution: Find A : C; of A : B = 6 : 7 & B : C = 8 : 7
\(\frac{A}{C}=\frac{A}{B} \times \frac{B}{C}\)= \(\frac{6}{7} \times \frac{8}{7}\)
= \(\frac{48}{49}\)
∴ A : C = 48 : 49.
2. If A: B=2: 3, B: C=4:5 and C:D = 6:7,let us find A:D
Solution: \(\frac{A}{D}=\frac{A}{B} \times \frac{B}{C} \times \frac{C}{D}=\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7}=\frac{16}{35}\)
∴ A : D = 16 : 35.
3. If A: B=3: 4 and B: C = 2:3, let us find A: B: C.
Solution: Find A : B : C, if A : B = 3 : 4 & B : C = 2 : 3
A : B = 3 : 4
B : C = 2 : 3 = 4 : 6
∴ A : B : C = 3 : 4 : 6.
4. If x y = 2:3 and y: z = 4: 7 let us find x:y: z.
Solution: x : y = 2:3=8:12
y: z = 4:7 =12:21
x:y: z= 8: 12:21
Question 15.
1. If x : y = 3 : 4, let us find (3y-x): (2x + y).
Solution: If x : y = 3 : 4,
find (3y – x) : (2x + y)
Let x = 3k & y = 4k (where k is a real no & k ± 0)
∴ \(\frac{3 y-x}{2 x+y}=\frac{3 \times 4 k-3 k}{2 \times 3 k+4 k}=\frac{12 k-3 k}{6 k+4 k}=\frac{9 k}{10 k}=\frac{9}{10}=9: 10\)
∴ (3y – x) : (2x + y) = 9 : 10.
2. If a:b = 8: 7, let us show that (7a-3b): (11a-9b) = 7:5.
Solution: If a : b = 8 : 7; show that,
(7a – 3b) : (11a – 9b) = 7 : 5
Let a = 8k & b = 7k (where k is a real number & k ≠ 0)
∴ \(\frac{7 \mathrm{a}-3 \mathrm{~b}}{11 \mathrm{a}-9 \mathrm{~b}}=\frac{7 \times 8 \mathrm{k}-3 \times 7 \mathrm{k}}{11 \times 8 \mathrm{k}-9 \times 7 \mathrm{k}}=\frac{56 \mathrm{k}-21 \mathrm{k}}{88 \mathrm{k}-63 \mathrm{k}}=\frac{35 \mathrm{k}}{25 \mathrm{k}}=\frac{7}{5}=7: 5\)
∴ (7a – 3b) : (11a – 9b) = 7 : 5.
3. If p q = 5: 7 and p-q=-4, let us find the value of 3p+ 4q.
Solution: If p : q = 5 : 7 & p – q
= -4; find 3p + 4q
let p = 5kq &
q = 7k, (where k is a real number & k ≠ 0)
∴ 5k – 7k = -4 or -2k = -4
∴ k = 2
∴ 3p + 4q = 3 x 5k + 4 x 7k
= 15k + 28k
= 43k
= 43 x 2 = 86
3p + 4q = 86.
Question 16.
1. If (7x-5y): (3x+4y) = 7: 11, let us show that (3x-2y): (3x+4y) = 127: 473.
Solution: If (7x – 5y) : (3x + 4y) = 7 : 11, show that (3x – 2y) : (3x + 4y) = 127 : 473
\(\frac{7 x-5 y}{3 x+4 y}=\frac{7}{11}\)or, 11 x (7x – 5y) = 7 x (3x + 4y)
or, 77x – 55y = 21x + 28y
or, 77x – 21x = 28y + 55y
or 56x = 83y
∴ \(\frac{x}{y}=\frac{83}{56}\)
Let x = 83k & y = 56k, (where k is a real number & k ≠ 0)
∴ (3x – 2y) : (3x + 4y)
= (3 x 83k – 2 x 56k) : (3 x 83k + 4 x 56k)
= (249 – 112k) : (249k + 224k)
= 137k : 473k
= 137 : 473
∴ (3x – 2y) : (3x + 4y) = 137 : 473 Proved.
2. If (10x+3y): (5x+2y)=9:5, let us show that (2x + y): (x+2y) = 11 : 13.
Solution: If (10x + 3y) : (5x + 2y) = 9 : 5,
show that (2x + y) : (x + 2y) = 11 : 13.
\(\frac{10 x+3 y}{5 x+2 y}=\frac{9}{5}\)or, 5(10x + 3y) = 9(5x + 2y)
or, 50x + 15y = 45x + 18y
or, 50x – 45x = 18y – 15y
∴ \(\frac{x}{y}=\frac{3}{5}\)
Let x = 3k & y = 5k, (where k is a real number & k ≠ 0)
∴ (2x + y) : (x + 2y)
= (2 x 3k + 5k) : (3k + 2 x 5k) = (6k + 5k) : (3k + 10k)
= 11k : 13k = 11 : 13
∴ (2x + y) : (x + 2y) 11 : 13 Proved.
Question 17.
1. Let us calculate what term should be added to both terms of the ratio 2: 5 to make the ratio 6:11.
Solution: Let x be the number which should be added with both the terms of 2:5 to get the ratio of 6:11.
∴ \(\frac{2+x}{5+x}=\frac{6}{11}\)
or, 6(5 + x) = 11(2 + x)
or, 30 – 22 = 11x – 6x
or, +8 = +5x
∴ x = \(\frac{8}{5}\)
∴ The required number = \(\frac{8}{5}\).
2. Let us calculate what term should be subtracted from each term of the ratio a: b to make the ratio m : n.
Solution: Let the number = x.
∴ \(\frac{a-x}{b-x}=\frac{m}{n}\)
or, an – nx = bm – mx
or, mx – nx = bm – an
or, x(m – n) = bm – an
∴ \(x \frac{b m-a n}{m-n}\)
∴ The required number = \(\frac{b m-a n}{m-n}\)
3. What term should be added to the antecedent and subtracted from the consequent of ratio 4: 7 to make a compound ratio of 2: 3 and 5: 4?
Solution: Let the required number = x
According to the problem,
\(\frac{4+x}{7-x}=\frac{2}{3} \times \frac{5}{4} \text { or, } \frac{4+x}{7-x}=\frac{5}{6} \text { or } 6 \times(4+x)=5 \times(7-x)\)or, 24 + 6x = 35 – 5x
or, 6x + 5x = 35 – 24
11x = 11
∴ \(x=\frac{11}{11}=1\)
∴ The required number = 1.
Application 1. Let us see whether the four numbers 2, 3, 4, and 6 are in proportion or not.
Solution: 2 x 6=3 x 4 and 3 x 4 =2×6
2:3::4:6
Application 2. Let us see whether the four numbers 2.5, -2, -5, and 4 are in proportion or not.
Solution: 2.5 x 4 =(-2) x (-5) and (-2) x (-5)=2.5 x 4
Application 3. Let us see whether four the numbers 2, 7, 12, and 42 are in proportion or not.
Solution: 2 x 42 = 84 &.7 x 12 = 84
2:7:: 12:42 (Are in proportion)
Application 4. Let us see whether four terms -√2, 6, 1, and √18 are in proportion or not.
Solution:
Four terms -√2, 6, 1, and √18
(-√2) * (-√18)
= √36
= 6. & 6 1=6
(√2):6::1: (√18) (Are in proportion).
Application 5. Let us see whether 2a, 3b, 6ac, and 9bc are proportional or not.
Solution: 2a x 9bc=18abc & 3b x 6ac=18abc
Application 6. Let us see whether 8x, 5yz, 40qx, and 25qyx are proportional or not.
Solution: 8x, 5yz, 40qx & 25qyz
8x x 25qyz = 200qxyz & 5yz x 40qx=200qxyz
8x 5yz: 40qx: 25qyz (Are in proportion).
Application 7. If 8: y:: 2:21, let us write by calculating the value of y.
Solution: If 8 : y:: 2:21, find the value of y.
Ans. 8 x 21 = y x 2 or 2y= 168
y=168/2
= 84.
The value of y = 84.
Application 8. Let us find the fourth proportion of 6, 9, and 12.
Solution: 6x = 9 x 12
x =9×12/6
= 18. Answer
The fourth proportion of 6, 9, and 12 is 18.
Application 9. Let us write by calculating the fourth proportion of 5, 4, 25.
Solution: Let the 4th proportional = x
5:4:: 25: x
or, 5x = 4 x 25
x = 4×25/5
=20.
Fourth proportional = 20 Answer
Application 10. Let us write by calculating how many independent proportions can be obtained from the proportional numbers 5, 6, 10, and 12 and mention those proportions.
Solution: 5, 6, 10, and 12 are proportional.
5:6::10: 12
1. 5, 10, 6, 12;
2. 6, 5, 12, 10;
3. 10, 5, 12, 6
These 3 are the different forms of proportion.
Application 11. Let us write by calculating which number is to be added to each of 12, 22, 42, and 72 to make the sums proportional.
Solution: 12, 22, 42, 72
Let x be the number which should be added with each term so that the sums will be proportional.
∴ (12 + x) : (22 + x) :: (42 + x) : (72 + x)
or, \(\frac{12+x}{22+x}=\frac{42+x}{72+x}\)
or, 864 + 72x + 12x + x2 = 924 + 42x + 22x + x2
or, 84x – 64x = 924 – 864
or, 20x = 60
∴ \(x=\frac{60}{20}=3\)
∴ The required number = 3.
Application 12. Let us write by calculating which number is to be added to each of 3.6, 7, and 10 to make the sums proportional.
Solution: Let the required number = x
∴ (3 + x) : (6 + x) :: (7 + x) : (10 + x)
∴ \(\frac{3+x}{6+x}=\frac{7+x}{10+x}\)
or, 30+10 x+3 x+x^2=42+7 x+6 x+x^2
30 + 13x = 42 + 13x.
∴ If any real number (≠ 0) is added, the sums will be in proportional.
Application 13. Let us find the 3rd proportion of 9 and 15.
Solution: x = 15×15 / 9
x=25
Application 14. Let us find 3rd proportional of Rs. 3 and Rs. 12.
Solution: Let the 3rd proportional = Rs x.
∴ \(\frac{3}{12}=\frac{12}{x}\)
or, 3x = 12 x 12
∴ \(x=\frac{12 \times 12}{3}=48\)
∴ 3rd proportional = Rs. 48
Application 15. Let us write by calculating the mean proportional of 0.5 and 4.5.
Solution: Let the 3rd proportional = x
∴ \(\frac{9 p q}{12 p q^2}=\frac{12 p q^2}{x}\)
∴ \(x=\frac{144 p^2 q^4}{9 p q}=16 p q\)
Application 16. If the extreme terms of three positive continued proportional numbers are pqr, pr/q let us find the mean proportional.
Solution: Mean proportional = √0.5×4.5= √2.25 1.5 Ans.
Application 17. Let us find the mean proportional of positive numbers xy2 and xz2 [Let me do it myself].
Solution: Mean proportional = \(\sqrt{x y^2 \times x z^2}=\sqrt{x^2 y^2 z^2}=x y z\)
