WBBSE Solutions For Class 10 Maths Chapter 7 Theorems Related To Angles In A Circle Exercise 7.2
Question 1. I drew a circle and I drew two angles in the segment in that circle which (a) are formed with the same arc; (b) are not formed with the same arc.
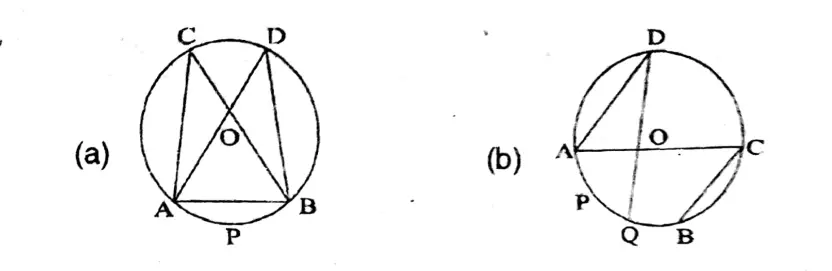
Question 2. I drew angles at the centre and the angle in the segment which (a) are formed with same arc; (b) are not formed with the same arc.
Read and Learn More WBBSE Solutions For Class 10 Maths
(a) In fig (1), the angle at the centre O and the angle in the segment are formed with the same arc.
(b) In fig (2) angle at the centre & angle in the segment are not formed with the same arc.

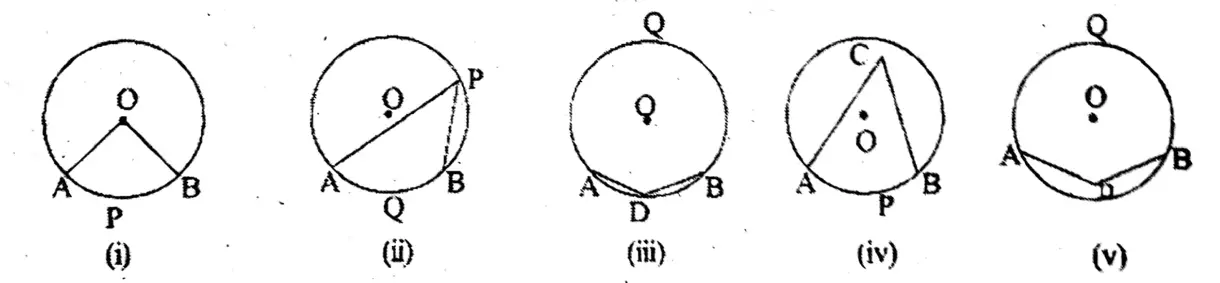
Question 3. Let us look at the picture and let us give an answer (O is the centre of the circle)
Solution:
(i) ∠AOB, is the angle at the centre of the arc APB.
(ii) ∠APB in the segment is formed with arc ÁQB
(iii) In fig (iii) ∠ADB is cyclically formed with arc AQB
(iv) In fig (iv) ∠ACB is cyclically formed with arc APB
(v) In fig (v) ∠ADB is not an angle in the segment formed with the arc AQB.

In fig. (i) two angles ∠ACB &∠ADB are in the same arc.
In fig. (ii)∠ACB & ∠ADB are two angles that lie in the segment ADCB.
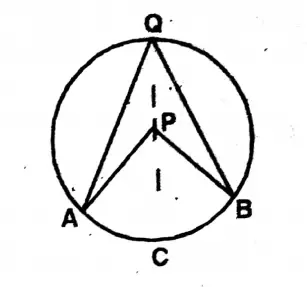
Question 4. I drew a circle with centre P and by drawing an angle ∠APB at the centre and an angle ∠AQB at the point on the circle by the arc ACB, we shall prove that, ∠APB2∠AQB
Solution:
I drew a circle with centre P and by drawing an angle∠APB at the centre and an angle ∠AQB at the point on the circle by the arc ACB
Let on the arc ACB of the circle with centre P, ∠APB is the angle at the centre & ∠AQB is the angle on the circumference.
To prove, ∠APB = 2 ∠AQB.
Join Q, P and produce to R.
Proof: In ΔAPQ, AP = PQ (Radii of the same circle)
∴ ∠PAQ = ∠AQP
Again, QP is produced to R.
∴ External ∠APQ = ∠PAQ + ∠AQP = ∠2AQP
Similarly, from ∠BQP, ∠BPR = 2∠BQP
∴ ∠APB = ∠APR + ∠BPR = 2 (∠AQP + ∠BQP)
= ∠AQB Proved
Question 5. The circle with centre O passes through three points A, B and C; if ∠ABO = 35° and ∠ACO = 45°, let us write by calculating the value of ∠BOC.
Solution:
Given
The circle with centre O passes through three points A, B and C; if ZABO = 35° and ZACO = 45°,
In ΔOAB, OA = OB (radii of the same circle) OAB= ∴ ∠OBA = 35°
In ΔOAC, OA = OC (radii of the same circle) OAC= ∴ ∠OCA = 45°
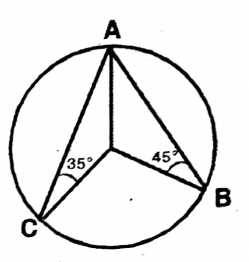
Solution: ∠BAC = 35° + 45° 80°
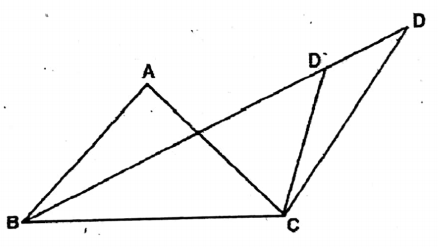
Question 7. ABC is an isosceles triangle with sides AB = AC; we draw ADBC in such a way that △DBC and △ABC lie on the same side of BC and ∠BAC = 2/BDC. Let us prove that the circle drawn with centre A and with radius AB is passing through point D, i.e., point D lies on the circle.
Solution:
Given
ABC is an isosceles triangle with sides AB = AC; we draw ADBC in such a way that ADBC and AABC lie on the same side of BC and ZBAC = 2/BDC.
Proof: Let the circle is not passing through D. If cuts BD at D’.
Join C, D’.
Now, BAC is the angle at the centre of the circle with
centre A and BDC is the angle on the circumference on
the same arc.
∴ ∠BAC = 2 ZBDC
But BAC 2 ZBDC (given)
∴ ∠BDC = <BD’C
It is not possible until point D. Coincide with D’ as an external angle of a triangle cannot be equal with its internal opposite angle.
∴ Point D is on the circle.