WBBSE Solutions For Class 10 Maths Chapter 7 Theorems Related To Angles In A Circle Exercise 7.3

WBBSE Solutions For Class 10 Maths Chapter 7 Theorems Related To Angles In A Circle Exercise 7.3

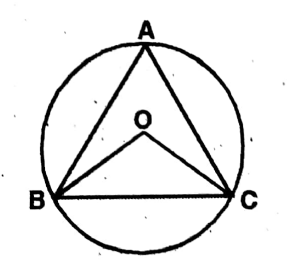
Question 1. O is the circumcentre of the isosceles triangle ABC, whose AB = AC, the points A and B, and C are on opposite sides of the center O. If ZBOC is 100°, let us write by calculating the values of ∠ABC and ∠ABO.

Solution: ‘O’ is the circumcenter of the isosceles triangle ABC, where AB = AC.

Join OB & OC.

Proof:

∴ ∠BOC is the angle at the centre & ∠BAC is the angle at the circumference on the same arcBC.

∴ \(\angle \mathrm{BAC}=\frac{1}{2} \angle \mathrm{BOC}=\frac{1}{2} \times 100^{\circ}=50^{\circ}\)

Again, as AB = AC,

∴ ∠ABC = ∠ACB

In ΔABC,

\(\angle \mathrm{BAC}+\angle \mathrm{ABC}+\angle \mathrm{ACB}=180^{\circ} \text { or, } 50^{\circ}+\angle \mathrm{ABC}+\angle \mathrm{ABC}=180^{\circ}\)

∴ \(50^{\circ}+2 \angle \mathrm{ABC}=180^{\circ}\)

∴ \(2 \angle \mathrm{ABC}=180^{\circ}-50^{\circ}=130^{\circ}\)

∴ \(\angle \mathrm{ABC}=\frac{130^{\circ}}{2}=65^{\circ}\)

Again, in ΔOBC, OB = OC (Radii of same circle).

∴ ∠OBC = ∠OCB

In ΔBOC, ∠BOC + ∠OBC + ∠OCB = 180°

or, 100° + 2∠OBC = 180°

∴ 2∠OBC = 180° – 100° = 80°

∴ \(\angle \mathrm{OBC}=\frac{1}{2} \times 80^{\circ}=40^{\circ}\)

Now, ∠ABO = ∠ABC – ∠OBC = 65° – 40° = 25°

∴ ∠ABC = 65° & ∠ABO =  25°

 

Read and Learn More WBBSE Solutions For Class 10 Maths

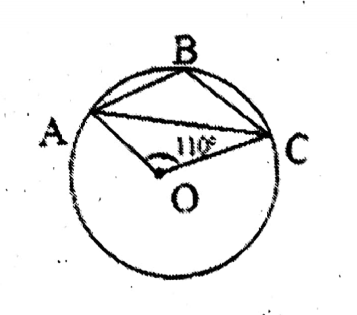
Question 2. In the adjoining, if O is the center of the circumcircle of ΔABC and ∠AOC = 110°; let us write by calculating the value of ∠ABC.

Solution:

Given

In the adjoining, if O is the center of the circumcircle of AABC and ZAOC = 110°

In the ∠AOC = 110°

∴ ∠ ABC = 1/2 of the angle at the center

= 1/2 x reflex AOC

= 1/2 x 250°

=125°

∠ ABC =125°

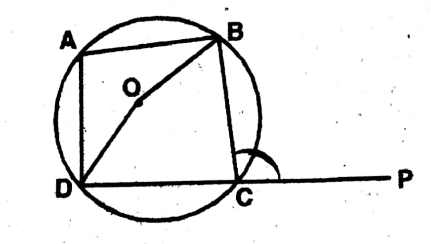
Question 3. ABCD is a cyclic quadrilateral of a circle with center O; DC is extended to point P. If ∠BCP = 108°, let us write by calculating the value of ∠BOD.

Solution:

Given

ABCD is a cyclic quadrilateral with the center of the circle O.

Side DC is produced to P such that BCP = 108°

Find ∠BOD.

∠BCD + BCP = 180°

∠BCD 180°- ∠BCP 180° – 108° = 72°

∠BOD = 2 x <BCD

= 2 x 72° = 144°

& Reflex ∠BOD = 360° – 144°

∠BOD = 216°.

Question 4. O is the center of the circle; ∠AOD = 40° and ∠ACB = 35°; let us write by calculating the value of ∠BCO and ∠BOD, and answer with reason.

Solution:

Given

O is the center of the circle ∠AOD = 40° & ∠ACB = 35°.

Find ∠BCO & BOD.

Produce CD, which cuts the circle at E.

∠AOE is the angle at the center and ∠ACE is the angle at the circumference on the same arc AE.

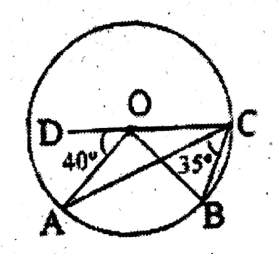
∴ ∠ACE = 1/2 

AOE = 1/2 x 40° = 20°

Now, ∠BCO = ∠BCA + ∠ACO

= ∠ACB + ∠ACE

= 35° + 20°

= 55°.

Again, ∠AOB is the angle at the center & ∠ACB is the angle at the circumference.

∴ ∠AOB = 2 x ∠ACB = 2 x 35° = 70°

∠BOD = ∠AOB+∠AOD

= 70° + 40°

= 110°

∴ ∠BCO = 55°

& BOD = 110°

Question 5. O is the center of the circle in the picture beside, if ∠APB = 80°, let us find the sum of the measures of ∠AOB and COD and answer with reason.

Solution:

Given

‘O’ is the center of the circle & ∠ADB = 80°.

To find the sum of ∠AOB + ∠COD.

Join B, C.

As ∠AOB is the angle at the center and DBC is the angle at the circumference on the same arc AB.

∴ ∠AOB = 2 x ∠ACB

Again, COD is the angle at the center and DBC is the angle at the circumference on the same arc CD.

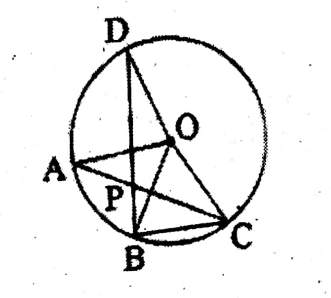
∠COD=2x ∠CBD

∠AOB+∠COD = 2x (∠ACB + ∠CBD)———(1)

Now, in ABCP, the side CP is produced to A.

∴ External BPA = <PCB + <PBC

∠APB = ∠ACB + <DBC

= ∠ACB+∠DBC= ∠APB = 80°————-(2)

Now, from (1) & (2), ∠AOB + ∠COB = 2 x (∠ACB + ∠DBC)= 2 x 80° = 160°.

Question 6. Like the adjoining figure, we draw two circles with centers C and D which inter- sect each other at points A and B. We draw a straight line through point A which intersects the circle with center C at point P and the circle with center D at point Q.

1. ∠PBQ = <CAD;

2. BPC = <BQD.

Solution: Two circles with centers C & D intersect each other at A & B.

A straight line passing through A cuts the circles at P & Q respectively.

To prove : 

∴ 1. ∠PBQ = ∠CAD

& 2. <BPC = <BQD.

Join A, B; A, C; P, C; A, D; D, Q; B, P; B, Q; B, C; B, D.

In the circle with center C,

∠ACP is the angle at the center &

∠ABP is the angle at the circumference on the same arc AP.

∴∠ABP =1/2 ∠ACP and CAP CPA [as, CA = CP (same radius)]

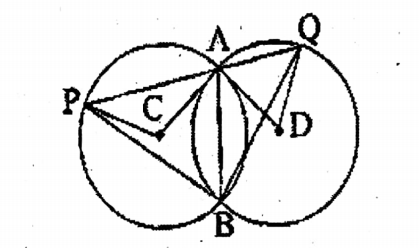
Now, in ∠CAP, ∠CAP + ∠CPA + ∠ACP = 180°

or, ∠CAP + ∠ACP = 180°

or, ∠CAP 180° – ∠ACP

∴∠CAP 90° – 1/2 

∠ACP 90°= ∠ABP

∴ ∠CAP 90°-∠ABP——(1)

Again, in the circle with center D,

∠ADQ is the angle at the center and ∠ABQ is the angle at the circumference on the same arc AQ.

∴∠ABQ= 1/2  ∠ADQ

In ∠ADQ, DA = DQ (radii of the same circle)

∴ ∠DAQ = ∠DQA

∴ ∠DAQ + ∠DQA = 2 ∠DAQ

In∠ADQ, ∠ADQ+ ∠DAQ + ∠DQA = 180°

or, ∠ADQ+2∠DAQ = 180°

or, 2 ∠DAQ 180° – ∠ADQ

∴∠DAQ = 90° – 1/2 

∠ADQ 90° – ABQ————-(2)

∴∠DAQ = 90° – ∠ABQ

Adding (1) & (2),

∠CAP +∠DAQ = 90° – ∠ABP + 90° – ∠ABQ

=180° (∠ABP + ∠ABQ) = 180° – ∠PBQ.

or, ∠PBQ = 180° – (∠CAP + ∠DAQ)

∴∠PBQ = CAD Proved.

Again, In ∠ABC, CA = CB (Radii of the same circle)

∠CAB = <CBA

& In ∠DAB, DA = DB (Radii of the same circle)

∴ ∠DAB = DBA

∴∠CAB+ ∠DAB = ∠CBA + ∠DBA

∠CAD = CBD but ∠CAD =∠PBQ (Proved before)

∴ ∠CBD = CAD =∠PBQ

∴ ∠CBD + ∠PBD =∠PAD+ ∠PBQ

or, CBP = DBQ [as BC= PC (Radii of same circle)] and BD = DQ

∴ ∠BPC = CBP and ∠DBQ = ∠BQD

∴ BPC = CBP =∠DBQ =∠BQD

∴ ∠BPC = ∠BQD Proved.

Question 7. If the circumcentre of triangle ABC is O; let us prove that ∠OBC + <BAC = 90°.

Solution:

Given

O is the circumcentre of the triangle ∠ABC.

To prove, ∠OBC + ∠BAC = 90°

BOC = 2BAC

∴ <BAC = 1/2 ∠BOC

In ΔOBC, ∠OBC = ∠OCB

∠OBC+∠OCB + ∠BOC = 180°

∴2∠OBC+BOC = 180°

or, 2∠OBC= 180° – ∠BOC

or, ∠OBC= 90° – 1/2 ∠BOC

= 90-∠BAC

∴∠OBC+∠BAC

= 90° Proved.

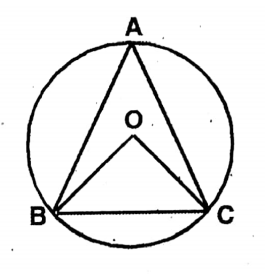
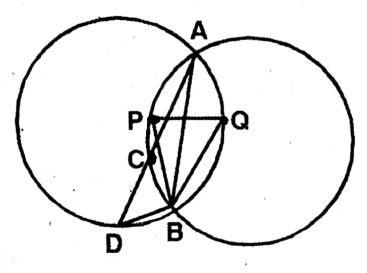
Question 8. Each of two equal circles passes through the center of the other and the two circles intersect each other at points A and B. If a straight line through point A intersects the two circles at points C and D, let us prove that ABCD is an equilateral triangle.

Solution:

Given

Each of two equal circles passes through the center of the other and the two circles intersect each other at points A and B. If a straight line through point A intersects the two circles at points C and D

Let P & Q are the centres of two equal circles. They cut each other at A and

Join, A,P; A,Q; B,P; B,Q; A,B; P,Q.

∴AP = BP = ΔAB = AQ = PQ

∴ΔAPQ & BQ are equilateral triangles.

∴∠PAQ=  ∠APQ= ∠AQP = ∠PBQ = ∠BPQ = ∠BQP = 60°.

Now, ∠APB =∠APQ+ ∠BPQ = 60° + 60° = 120°

∠AQB = ∠AQP+∠PQB = 60° +60° = 120°

∴ ∠APB = ∠AQB = 120°

In the circle with centre P, APB is the angle at the centre & ADB is the angle at the circumference on the same arc AQB.

∴∠ADB = 1/2 

∠APB = 1/2  x 120° = 60°

∠CDB = 60°

Again, in the circle with center Q, ZAPB & ZACB are the angles at the circumference on the same arc.

∠ACB = ∠APB = 120°.

∴∠BCD = 180° – ∠ACB= 180°- 120° = 60°

∴ In ABCD, CDB = ∠BCD = 60°

Remaining DBC= 180° (∠CDB + <BCD) 

= 180° – (60° 60°) = 60°

∴ All the angles of BCD are equal.

∴ ABCD is an equilateral triangle.

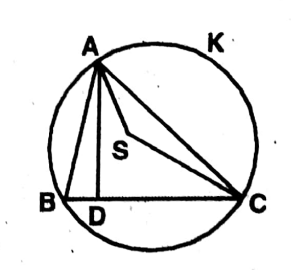
Question 9. S is the center of the circumcircle of AABC and if ADI BC, let us prove that <BAD = <SAC.

Solution: S is the circumcenter of △ABC & AD ⊥ BC.

To prove, ∠BAD = ∠SAC

Join, S, A & S, and C.

Proof: SA = SC (Radii of same circle)

Again, in △SAC, AS = SC

∠SAC = ∠SCA

Again, in △SAC,

∠ASC + ∠SAC + ∠SAC = 180°

or, ∠ASC + 2∠SAC = 180° [∵ ∠SAC = ∠SCA]

∴ 2∠SAC = 180° – ∠ASC

or ∠SAC = \(90^{\circ}-\frac{1}{2} \angle \text { ASC }\)          …(1)

Again, in the circle with center S, ∠ASC is the angle at the centre & ∠ABC is the angle at the circumference on the same arc ∠AKC.

∴ \(\angle \mathrm{ABC}=\frac{1}{2} \angle \mathrm{ASC}\)          …(2)

∠SAC = 90° – ∠ABC       …(3)

in ∠ABD, ∠ADB = ∠ADC = 90°

∴ ∠ADB + ∠BAD  = 90°

or, ∠BAD = 90° – ∠ADB = 90° – ∠ABC       …(4)

∴ From (3) & (4), ∠SAC = ∠BAD        Proved.

 

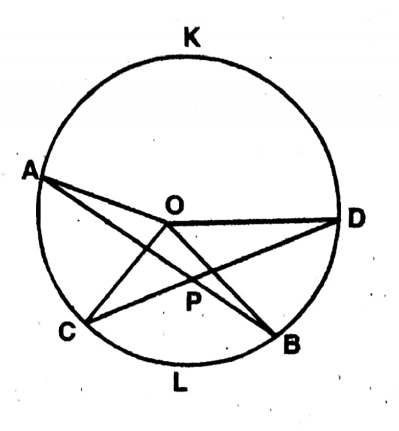
Question 10. Two chords AB and CD of a circle with center O intersect each other at the point P, let us prove that ∠AOD + ∠BOC = 2∠BPC. If ∠AOD and ∠BOC are supplementary to each other, let us prove that the two chords are perpendicular to each other.

Solution:

Given

Two chords AB & CD of a circle with center O,

intersect each other at P.

To prove,

∠AOD + ∠BOC = 2BPC

If ∠AOD & BOC are supplementary to each other, then prove that the chords are perpendicular to each other.

Join, O, A; O, B; O, C; O, D; & B, D.

In the circle with center O, AOB is the angle at the center & ABD is the angle at the circumference, in the same arc AKD.

∴∠ABD = 1/2 = ∠AOD

or, ∠AOD = 2 x ∠ABD

Again, in the circle with center O, ∠BOC is the angle at the center and BDC is the angle at the circumference on the same arc ZBLC.

∴∠BOC = 2 x <BDC

∴∠AOD + ∠BOC = 2(∠ABD + 2BDC) = (<PBD + BDP)——(1)

Now in the triangle PBD, Ext. ∠BPC

∴ ∠BPC = ∠PBD + 2BDP

From (1), ∠AOD +∠BOC = 2∠BPC (Proved 1st part)

Again, if ∠AOD + ∠BOC = 2 right angles

2 x ∠BPC =∠AOD +∠BOC = 2 right angles

∴∠BPC = 90°

BP PC, i.e., Two chords AB & CD are perpendicular to each other. Proved – 2nd part.

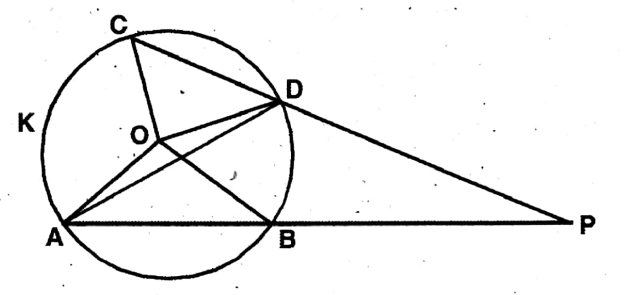
Question 11. If two chords AB and CD of a circle with center O, when produced, intersect each other at the point P, let us prove that ∠AOC – BOD = 2∠BPC.

Solution:

Given

Two chords AB and CD of the circle with center O, when produced, cut each other at P, outside the circle.

To prove, ∠AOC – BOD = 2 x <BDC

Join O, A; O, B; O, C; O, D; & A, D.

Proof: In the circle with center O,∠AOC is K

the angle at the center & ZADC is the angle at the circumference on the same arc. AKC, 

∴ ∠AOC = 2∠ADC

Again, in that circle BAD is the angle at

the center & BAD is the angle at the circumference on the same arc BD,

∴ ∠BOD = 2∠BAD

∠AOC – ∠BOD=2(∠ADC-∠BAD) —–(1)

In ΔAPD, External ∠ADC = ∠APD + ∠PAD = ∠APC + ∠PAD

or, ∠APC =∠ADC – ∠PAD

2(∠ADC-∠PAD) 2∠APC

∠AOC –

BOD = 2∠APC [from (1)]

Question 12. We drew a circle with point A of quadrilateral ABCD as the center which passes through points B, C, and D. Let us prove that CBD + /CDB = <BAD.

Solution: The circle is drawn with center A of the quadrilateral ABCD, passing through B, C, and D.

To prove, CBD + /CDB = 1/2 ∠BAD

Proof : 2∠BCD = 360 – <BAD

∴∠BCD = 180° -1/2 ∠BAD

From ABCD, ∠BDC + 4CBD = 180° – ∠BCD

or, <CBD + /CDB = 180° – (180° -1/2 ∠BAD) 

=1/2 ∠BAD Proved.

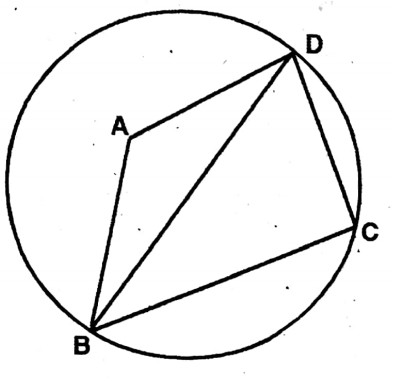
Question 13. O, is the circumcentre of AABC and OD is perpendicular on the side BC; let us prove that BOD = <BAC

Solution: O is the circumcentre & OD is perpendicular to BC. 

To prove,∠BOD = BAC

Join O, A; O, B; O, C; O, D &A, D. 

Proof: From ΔAOC, 

∠AOC+∠OAC+∠OCA = 180°

.. 2∠OAC = 180° – ∠AOC 90° – ∠ABC

∠BAD 90° – ∠ABC =∠OAC

.. <BAC = ∠OAC + ZOAB = ∠BOD Proved.

Chapter 7 Theorems Related To Angles In A Circle Exercise 7.3 Multiple Choice Question

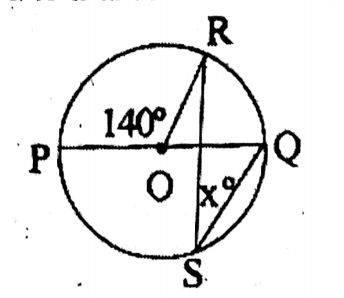
Question 1. In the adjoining figure, If ‘O’ is the center of the circle and PQ is a diameter then the value of x is

1. 140
2. 40
3. 80
4. 20

Solution: ∠ROQ 180° 140° = 40°

.. x = <RSQ = 1/2 x 40° = 20°

Answer: 4. 20°

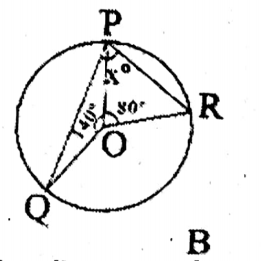
Question 2. In the adjoining figure, if O is the center of circle, then the value of x is

1. 70
2. 60
3. 40
4. 200

Solution: ∠BOR = 360° (140° +80°) = 360° 220° = 140°

∴∠QPR = 1/2  ZQOR= 1/2 x 140° = 70°

Answer. 2. 70°

Question 3. In the adjoining figure, if O is the center of the circle and BC is the diameter then the value of x is

1. 60
2. 50
3. 100
4. 80

Solution:∠AOC 1800° – 80° = 100°

∴∠ADC = x2 = 100°/ 2

= 50°

Answer. 2. 50°

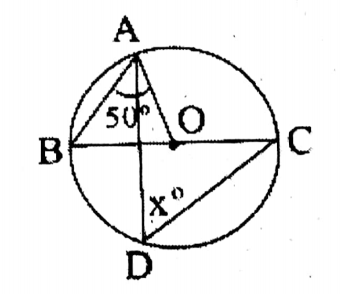
Question 4. If O is the circumcentre of AABC and ZOAB = 50°, then the value of ZACB is

1. 50°
2. 100°
3. 40°
4. 80°

Solution: If ∠OAB = 50°

∠AOB 180°

(50° + 50°) = 180° – 100° = 80°

∴ ∠ACB = 1/2

AOB = 1/2 x 80° = 40°

Answer. 3. 40°

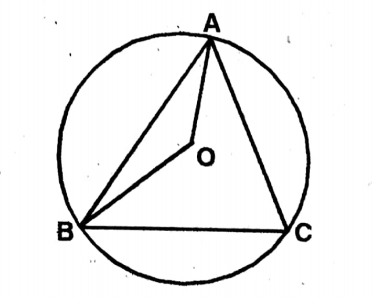
Question 5. In the adjoining figure, if O is centre of circle, the value of POR is

1. 20°
2. 40°
3. 60°
4. 80°

Solution: ∠POQ = 180° –  20° = 160°

∠QOR = 180° – 80° = 100°

∠POR 160° – 100° = 60°

Answer. 3. 60°

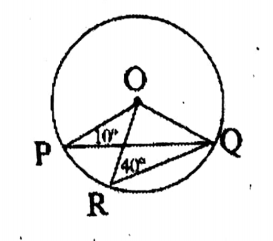
Chapter 7 Theorems Related To Angles In A Circle Exercise 7.3 True or False

1. In the adjoining figure, if O is the center of the circle, then ∠AOB = 2∠ACD.

False

2. point O lies within the triangular region ABC in such a way that OA OB and ZAOB = 2ZACB. If we draw a circle with centre O and length of radius OA, then the point C lies on the circle. 

True

Chapter 7 Theorems Related To Angles In A Circle Exercise 7.3 Let us Fill in the blanks

1. The angle at the Half center is the angle on the circle, subtended by the same arc.

2. The lengths of two chords AB and CD of a circle with centre O are equal. If APB and AQC are angles on the circle, then the values of the two angles are  Equal.

3. If O is the circumcentre of an equilateral triangle, then the value of the from angle formed by an side of the triangle is  120°.

Chapter 7 Theorems Related To Angles In A Circle Exercise 7.3 Short answers

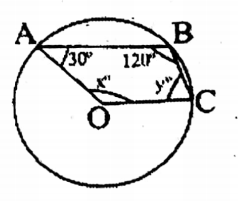
Question 1. In the adjoining figure, O is the center of the circle, if ∠OAB = 30°, ∠ABC = 120°,∠BCO = y° and ∠COA = x°, let us find x and y. 

Solution.

Given

In the adjoining figure, O is the center of the circle, if ∠OAB = 30°, ∠ABC = 120°,∠BCO = y° and ∠COA = x°

∠AOC = x° 360°- 2 x 120° = 120°

∠BCO = y°

=360° -2(120° +30° + 120°) = 360°

Question 2. O is the circumcentre of the triangle ABC and D is the midpoint of the side BC. If <BAC 40°, let us find the value of BOD. 

Solution. BOC = 2BAC = 2 x 40° = 80°

<BOD= (90° –  180-80 / 2)

= 90° – 50° = 40°

Question 3. Three points A, B, and C lie on the circle with center O in such B a way that AOCB is a parallelogram, let us calculate the value of the side ZAOC.

Solution. ∠AOC 360°-2/ABC

=1/3 x 360° = 120°

Question 4. O is the circumcentre of the isosceles triangle ABC and ABC= 120°; if the length of the radius of the circle is 5 cm, let us find the value of the side AB.

Solution. 

Given

O is the circumcentre of the isosceles triangle ABC and ABC= 120°; if the length of the radius of the circle is 5 cm

∠ACB = 180°-120° /2  = 30°

∴∠AOB 60°

As OA = OB,

∴ ∠OAB ∠OBA = 60°

∴ OA OB = AB = 5 cm.

Question 5. Two circles with centers A and B intersect each other at points C and D. The center B of the other circle lie on the circle with center A. If ZCQD = 70°, let us find the value of ZCOD.

Solution.

Given

Two circles with centers A and B intersect each other at points C and D. The center B of the other circle lie on the circle with center A. If ZCQD = 70°,

CAD (360°-4 x 70) = 80°

∠CPD= 1/2 ZCAD = 1/2 x 80° = 40°

Example :

Each semi-circle angle is one right angle.

All the semicircle angles are equal.

∠APB =∠AQB = ∠ARB =∠ASB.

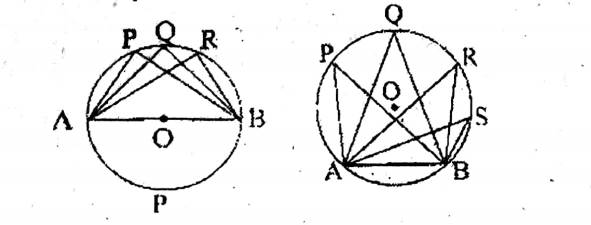
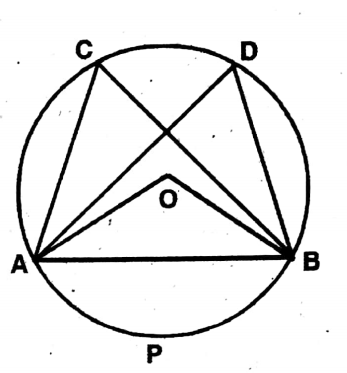
Question 6. Let us prove that all angles of a circle formed by the same arc are equal.

Solution: Let in the circle with center O, ∠ACB &∠ADB are the two angles at the circumference on the same arc ∠APB. 

To prove ∠ACB = ∠ADB.

Join O, A & O, B.

As on the arc ∠APB, AOB is the angle at the center and ∠ACB

& ∠ADB is the angles on the circumference.

∴∠AOB = 2∠ACB & ∠AOB = 2∠ADB

∴ ∠ACB = ∠ADB Proved.

Question 7. Let us prove that if all angles of a circle subtended by circular arcs be equal then the lengths of the arcs are equal.

Solution: Let O is the center of the circle & the angles ∠ACB, ∠ADB, and ∠AEB are the angles on the circumference are equal,

i.e.,∠ACB = ∠ADB = ∠AEB.

To prove that the angles are on an arc of equal length.

Proof: If the angle on the circumference is half of the angle at the center then they will be on the same arc.

∴ ∠AOB = 2∠ACB = 2∠ADB = 2∠AEB

∴ The angles on the same arc∠APB.

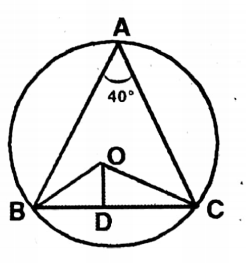
Question 8. Let us see the figure of the circle below and let us find the value of x. O is the center of the circle.

Solution: O is the center of the circle.

∠ABC and∠ADC are the front angles on the circle formed by the minor arc /CPA.

∴∠ABC = ∠ADC= 40° ( Given that ∠ADC = .40°)

and in ΔABC, ∠ABC + ∠ACB +∠BAC = 180°

∴ 40°+100° + x = 180°

or, x° 180° 140° = 40°

∴ x = 40.

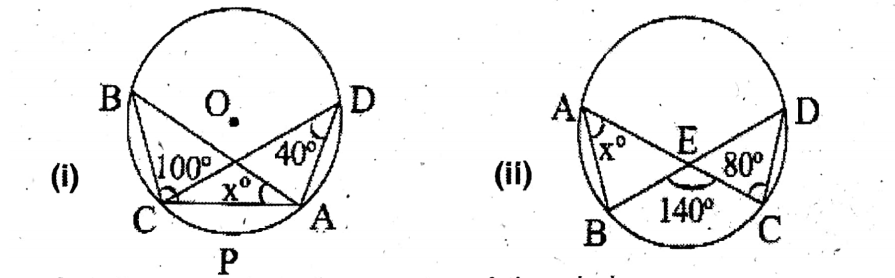
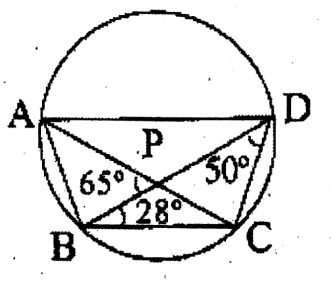
Question 9. In the adjoining figure, 65°. CBD = 28°; Let us determine the values of ∠ADB,∠ABD, <BAC, ∠ACB, CAD, and ∠ACD.

Solution:

In the adjoining figure, 65°. CBD = 28°;

<BAC = <BDC = 50° Again, ∠CAD = ADB = 28°

BDC = 50°, ∠APB = 28°

In ABPC, Exterior ∠APB = ∠PBC +∠PCB.

65° = 28° + ACB;

ACB = 37°

InΔABP ∠ABP + ∠BPA + ∠PAB = 180°

∠ABP = ∠ACB = 37°

∠ABP = ∠ADB = 37°

∠ACD = ∠ABD = 65°