WBBSE Solutions For Class 10 Maths Chapter 7 Theorems Related To Angles In A Circle Exercise 7.4
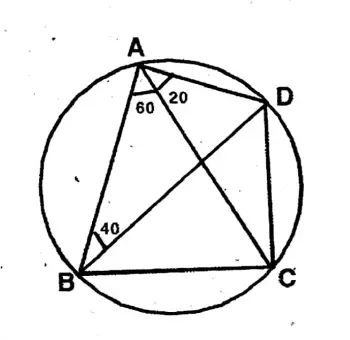
Question 1. In the adjoining figure, DBA = 40°, <BAC = 60°, and CAD = 20°; let us find the values of ZDCA and BCA. Also, let us see by calculating what the sum of BAD and ZDCB will be.
Read and Learn More WBBSE Solutions For Class 10 Maths
Solution:
Given
In the figure, DBA = 40°; <BAC = 60° & CAD = 20°.
<DCA & ∠DBA are the angles on the circumference on the same arc CD.
∴ ∠DCA =∠DBA = 40°
Now, BAD = <BAC + ∠CAD = 60° + 20° = 80°
The sum of the three angles of a triangle = 180°
∴ In ΔABD, <BAD + 2BDA +
∴ ∠BDA =180° – (BAD + ABD)
= 180 (80° + 40°)
= 180° -120° = 60°
ABD = 180°
∴ On the arc AB, the angle on the circumference ZBCA
ZBDA = 60°
∴ <BCD = ∠BCA + ∠ACD = 60° + 40° = 100°
∴ ∠BCD + ∠BAD
100° +80° = 180°
.. ∠DCA = 40°, ∠BCA = 60° & Sum of the ∠BAD + ∠BCD = 180°

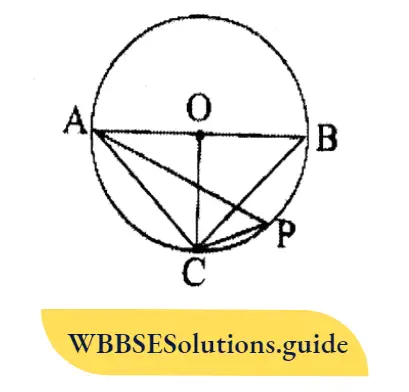
Question 2. In the adjoining figure, AOB is the diameter of the circle and O is the center of the circle. The radius OC is perpendicular on AB. If P is any point on minor arc CB, let us write by calculating the values of <BAC and ∠APC.
Solution:
Given
In the adjoining figure, AOB is the diameter of the circle and O is the center of the circle. The radius OC is perpendicular on AB. If P is any point on minor arc CB
As, AB LOC .. ∠AOC = ∠BOC = 90°
ΔAOC is an isosceles triangle.
.: AO = OC
∠OAC = ∠OCA
∠OAC+∠OCA = 90° [∠AOC = 90°]
or, ∠OAC+∠OAC = 90°
or, 2 ∠OAC = 90°
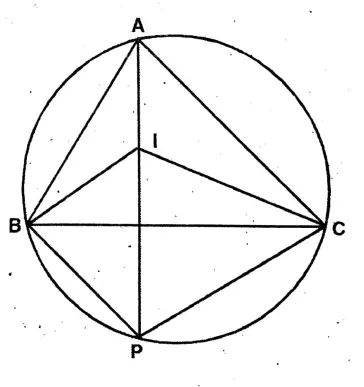
Question 3. O is the orthocentre of the triangle ABC and the perpendicular AD drew on BC when extended, Intersects the circumcircle of △ABC at point G; let us prove that OD = DG.
Solution:
Given
O is the orthocentre of the triangle ABC and the perpendicular AD drew on BC when extended, Intersects the circumcircle of AABC at point G
To prove, OD = DG.
Join B, G & C, G.
Proof: In the circumcircle of the ABC,
∠ACB is the angle on the circumference on arc AB.
∴ ∠ACB = ∠AGB
or, ∠ACB = ∠OGB
∠ECD = ∠OGB = ∠BGO———-(1)
Again, BEL AC & AD 1 BC.
∠OEC = ∠ODC = 90°
∠OEC+∠ODC= 90° + 90° = 180°
In the quadrilateral ODCE,
∠OEC+∠ECD +∠ODC +∠DOE = 4 right angles ∠ECD + ∠DOE
= 4 right angles (∠OEC + ∠ODC) 4 right angles – 2 right angles
= 2 right angles ∠ECD + ∠EOD =∠EOD + ∠BOD
∴∠ECD = <BOD = ∠BOG——-(2)
From (1) & (2), BGO = BOG
BG = BO
Now in two right-angled triangles,
Hypotenuse BG = Hypotenuse BO, BD is common.
∴ ABDG ≅ ABDO.
∴ OD = DG Proved.
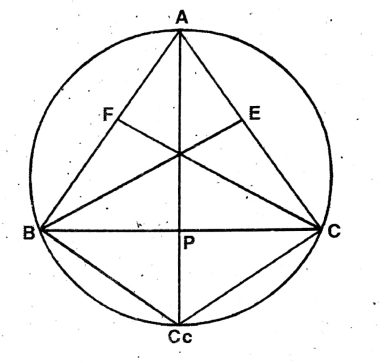
Question 4. I is the center of the incircle of AABC; Al produced intersects the circumcircle of that triangle at the point P, let us prove that PB = PC = PI
Solution:
I is the center of the incircle of △ABC; Al produced intersects the circumcircle of that triangle at the point P,
To prove PB = PC = PI
Join B, I; C, I; & P, B; P, C.
∴ The bisectors of the angles of a triangle meet at a point called In-centre.
∴ ∠BAI = ∠CAI = A/2,
∠ABI = ∠CBI = B / 2
∠ACI = ∠BCI = C/2
∠PBC & PAC arc the angles of the circumcircle of
ΔABC, on the arc PC.
∴∠PBC=∠PAC
Now, ∠IBP = ∠PBC + ∠CBI = ∠PAC + ∠CBI = ∠CAI + ∠CBI
A/ 2 + B/2 ———-(1)
The external angle of the ΔABI, ∠BIP = ∠BAI + ∠ABI =
A/2 + B/2
From (i) & (ii), ∠IBP = ∠BIP. In ΔPBI, ∠IBP = ∠BIP
∴ BP = PI——-(3)
Similarly, in∠PCI, ∠ICP = CIP
i.e. PC = PI———-(4)
∴ From (3) & (4), PB
PC = PI Proved.
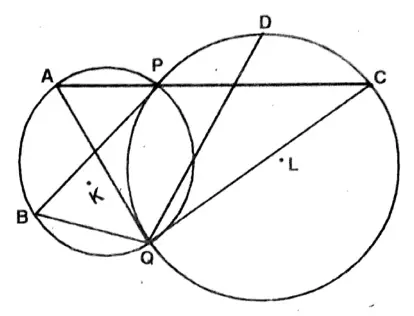
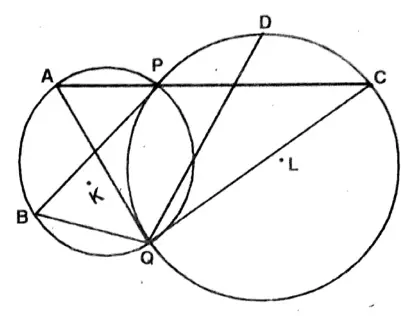
Question 5. Timir drew two circles that intersect each other at points P and Q. Through the point P two straight lines are drawn so that they intersect one of the circles at points A and B, and the other circle at points C and D respectively; let us prove that ∠AQC = ∠BQD.
Solution:
Given
Timir drew two circles that intersect each other at points P and Q. Through the point P two straight lines are drawn so that they intersect one of the circles at points A and B, and the other circle at points C and D respectively
To prove, ∠AQC = ∠BQD.
Join A, Q, B, Q, C, Q & D, Q
Proof: In the circle with center L, ∠PCQ &∠PDQ are the angles on the same circumference.
∠PCQ =∠PDC——-(1)
Again, in the circle with center K, ∠PAQ = ∠PBQ———(2)
As these are angles on the same arc.
Adding (1) & (2),
∠PAQ + ∠PCQ = ∠PBQ+ ∠PDC———(3)
In AACQ sum of the three angles = 180°
∠CAQ + ∠ACQ + ∠AQC = 180°
or, ∠PAQ +∠PCQ + ∠AQC = 180°——–(4)
Similarly in ABDC, the sum of three angles = 180°
∴ ∠DBQ+∠BDQ+∠BQD = 180°
or, ∠PBQ + ∠PDQ+ ∠BQD = 180°——-(5)
From (4) & (5),
∠PAQ + ∠PCQ + ∠AQC = ∠PBQ + ∠PDQ + ∠BQD——–(6)
Subtracting (3) from (4),
∠AQC = ∠BQD Proved.
Question 6. Two chords AB and CD of a circle are perpendicular to each other. If a perpendicular drawn to AD from the point of intersection of those two chords AB and CD are produced to meet BC at point E, let us prove that point E is the midpoint of BC.
Solution:
Given
Two chords AB and CD of a circle are perpendicular to each other. If a perpendicular drawn to AD from the point of intersection of those two chords AB and CD are produced to meet BC at point E
In the circle, AB & CD are perpendicular to each other & intersect at O. The perpendicular from O on chord AD cuts the chord BC at E.
To prove, E is the midpoint of BC.
Proof: In ΔAFD, ∠AFO = 90° as OF AD
In ΔAFO, ∠FAO+∠AOF = 90°
i.e., ∠DAQ + ∠ADO = 90°—-(1)
Again, in ΔAOD, ∠AOD = 90° as AO ⊥ DO
∴∠DAQ +∠ADO = 90°——(2)
From (1) & (2),∠AOF = ∠ADO
or, ∠ADO = ∠EOB as ∠AOF ∠EOB (vertically oppo-site)
∴ ∠EOB = ∠ADO
Or, ∠EOB = ∠ADC
∴ ∠EOB = ∠ABC (Angles on the same circumference)
∴ ∠EOB = ∠OBC =∠OBE
In ΔOEB, ∠EOB =∠OBE.
∴ BE = OE—–(3)
∠AOF+∠DOF = 90° (as AOD = 90°)
and ∠AOF+∠DAF 90°
∴∠DOF = <DAO
or,∠COE = ∠DÁB [∠COE = vertically ∠DOF]
∴<COE = <DCB [COE & DCB are angled on the same circumference]
i.e., ∠COE = ∠OCE
InΔOCE, ∠COE = ∠OCE
∴CE = OF ——– (4)
From (3) & (4), BE = CE
∴ E is the midpoint of BC.
Question 7. If in a cyclic quadrilateral ABCD, AB = DC, let us prove that AC = BD.
Solution: ABCD is a cyclic quadrilateral, AB = DC. To prove AC = BD. Proof: Join A, C & B, D.
Let AC & BD intersect at E.
∠CAB & ∠DAB are the angles on the same circumference.
∴∠CAB = ∠CBD
i.e.,∠EAB = ∠CDE
In ∠AEB & ∠DEC,
∠EAB = <CDE
∠AEB = ∠DEC (vertically opposite)
& AB = DC (given)
∴ΔAEB ≅ ADCB. (AAS)
∴AE = DE & BE = CE
∴ AC = AE + CE = DE+ BE = BD
∴ AC = BD.
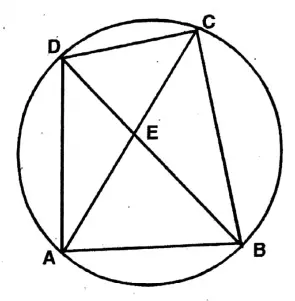
Question 8. OA is the radius of a circle with the center at O; AQ is its chord and C is any point on the circle. A circle passes through the points O, A; C intersects the chord AQ at the point P; let us prove that CP = PQ.
Solution:
OA is the radius of a circle with the center at O; AQ is its chord and C is any point on the circle. A circle passes through the points O, A; C intersects the chord AQ at the point P
Join O, A & O, Q.
Proof OQ & OA are two radii of the circle with center O.
In the isosceles ΔOQA,
∠OQA = ∠OAQ
Again, AO=CA is an isosceles triangle as OQ = OC (Radii of the same circle)
∴∠OQC = ∠OCQ
or, ∠OQA+∠AQC = ∠PCQ + ∠PCO
or, ∠OQA + ∠PQC = ∠PCQ + ∠PCO
∴ ∠PCO &∠PAO are the angles on the same circumference OP.
<PCO = <PAO = ∠OAQ (as ∠OQA = ∠OAQ)
∴ ∠PCO = ∠OQA
∴ ∠OAQ + ∠PQC = ∠PCQ + ∠OQA or, <PQC = ∠PCQ
∴ CP = PQ (As APCQ is an isosceles triangle).
Question 9. The triangle ABC is inscribed in a circle, and the bisectors AX, BY, and CZ of the angles <BAC, ZABC, and ZACB intersect at the points X, Y, and Z on the circle respectively, let us prove that AX is perpendicular to YZ.
Solution:
The triangle ABC is inscribed in a circle, and the bisectors AX, BY, and CZ of the angles <BAC, ZABC, and ZACB intersect at the points X, Y, and Z on the circle respectively
Join X, Y; Y, Z; Z, X.
Let AX cuts YZ at P.
∴∠AXY + Y = ∠AXY + ∠BYX + ∠BYZ
= ∠ABY+∠BAX + ∠BCZ
=∠A/2 + ∠B/2 + ∠C/2
=∠A+∠B+∠C/2
= 1 rt. angle
∴ In PYX, ∠YXP + ∠PYX = 1 rt. angle
∴ ZP = 1 rt. angle
∴ AX ⊥ YZ.
Question 10. The triangle ABC is inscribed in a circle. The bisectors of the angles <BAC, ∠ABC, and ∠ACB intersect at the points X, Y, and Z on the circle respectively, let us prove that in ΔXYZ, ∠YXZ = 90° – <BAC / 2
Solution: ΔABC is in a circle. Bisectors of <BAC, ∠ABC, & ∠ACB meet the circle at X, Y, and Z respectively.
To prove in ΔXYZ, ∠YXZ = 90° – 1/2 <BAC.
Proof: On the arc AY, ∠AXY = ZABY = 1/2 ZB
Similarly, on the arc AZ, ∠AXZ = ∠ACZ =1/2 ZC.
∴ Total ∠X = 1/2 ∠B + 1/2 ∠C
In ΔABC, 1/2 ∠A + 1/2 ∠B + 1/2 ∠C = 90°
1/2 ∠B + 1/2 ∠C = 90° – 1/2 ∠A
Or, ∠X = 90° – 1/2∠A
∴ ∠YXZ 90° – 1/2 <BAC.
Question 11. A perpendicular drawn on BC from point A of AABC intersects the side BC at point D and a perpendicular drawn on side CA intersects the side CA at the point E; let us prove that four points A, B, D, and E are concyclic.
Solution:
A perpendicular drawn on BC from point A of AABC intersects the side BC at point D and a perpendicular drawn on side CA intersects the side CA at the point E
Join D, E.
Proof: AD T BC & AE T CA
∴∠ADB = ∠ADC = 90°.
∠AEB = ∠BEC = 90°
∴ External EDC = internal opposite <BAE
∴<BDE + ∠EDC = 2 rt. angles
i.e., ∠BDE+∠BAE= 2 rt. angles
∴ Opposite angles of the quadrilateral are supplementary.
∴ Opposite angles or the cyclic quadrilateral are supplementary.
∴ A, B, D, E arc concyclic.
Chapter 7 Theorems Related To Angles In A Circle Exercise 7.4 Multiple Choice Question
Question 1. In the adjoining figure, O is the center of the circle, if ZACB = 30°, ZABC = 60°, ZDAB = 35° and ZDBC = x°, the value of x is
1. 35
2. 70
3. 65
4. 55
Solution. ∠BAC = 90°
∴ ∠BDC 90° – 35°= 55°
Answer: 4. 55°
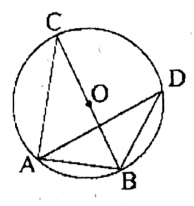
Question 2. In the adjoining figure, O is the center of the circle, if ∠BAD = 65°, BDC = 45°, then the value of CBD is
1. 65°
2. 45°
3. 40°
4. 20°
Solution: ∠CAD = ∠BAD – <BAC = 65° – 45° = 20°
∴ ∠CAD = CBD = 20°
Answer: 4. 20°
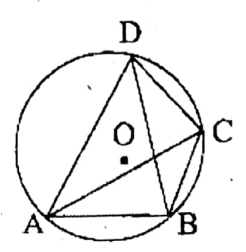
Question 3. In the adjoining figure, the O is the center of the circle, if ZAEB = 110° and CBE = 30°, the value of ∠ADB is
1. 70°
2. 60°
3. 80°
4. 90°
Solution: ∠ACB = ∠ADB = 180° – (70° + 30°) = 80°
Answer: 3. 80°
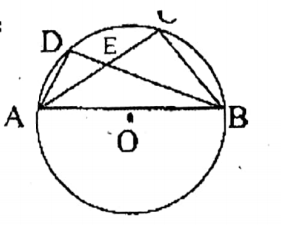
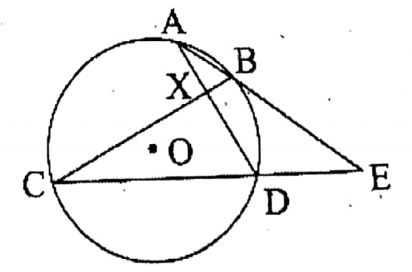
Question 4. In the adjoining figure, O is the center of the circle, if∠BCD = 28°, ∠AEC = 38° then the value of ∠AXB is.
1. 56°
2. 86°
3. 38°
4. 28°
Solution:
In the adjoining figure, O is the center of the circle, if∠BCD = 28°, ∠AEC = 38°
BCD = BAD = 28°
= ∠CBE 180° – (38° + 28°) 114°
∠ABX = 180° – 114° = 66°
∠AXB = 180° – (66° + 28°)= 86°
Answer: 2. 86°
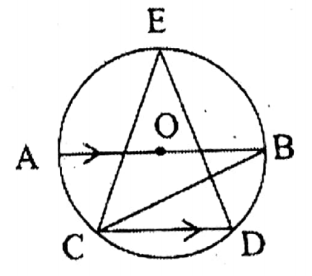
Question 5. In the adjoining figure, O is the center of the circle and AB is the diameter. If AB || CD, ZABC= 25°, the value of <CED is
1. 80°
2. 50°
3. 25°
4. 40°
Solution; ∠ABC= ∠BCD = 25° (alternate angle)
∴∠CED = 90° – 2 x 25° = 40°
Answer: 4. 40°
Chapter 7 Theorems Related To Angles In A Circle Exercise 7.4 True Or False
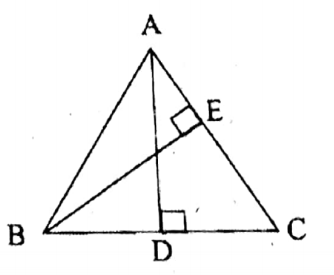
Question 1. In the adjoining figure AD and BE are the perpendiculars on sides BC and CA of the triangle ABC. A, B, D, and E are concyclic.
Solution: In AABC, AD & BE are the perpendiculars on BC and AC, respectively points A, B, C, D, and E are concyclic.
True.
Question 2. In ABC, AB = AC, BE, and CF are the bisectors of the angles B ABC and ACB and they intersect AC and AB at points E and F respectively. Four points B, C, E, and F, are not concyclic.
Solution: In ΔABC, AB = AC; BE & CF are the bisectors of ZABC & ZACB, respectively which cut at E & F.
Points B, C, E, and F are not concyclic.
True
Chapter 7 Theorems Related To Angles In A Circle Exercise 7.4 Fill In The Blanks
1. All angles in the same segment are Equal.
2. If the line segment joining two points subtends equal angles at two other points on the same side, then the four points are Concyclic.
3. If two angles on the circle formed by two arcs are equal then the lengths of the arcs Are equal.
Chapter 7 Theorems Related To Angles In A Circle Exercise 7.4 Short Answer
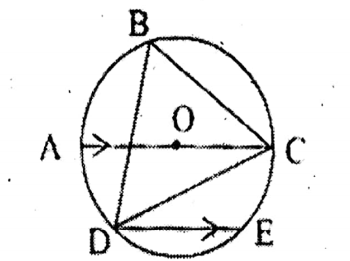
Question 1. In the adjoining figure, O is the center of the circle, AC is the diameter, and chord DE is parallel to the diameter AC. If CBD = 60°; let us find the value of ZCDE.
Solution:
In the adjoining figure, O is the center of the circle, AC is the diameter, and chord DE is parallel to the diameter AC. If CBD = 60°
∠CDE = 90°- ∠CBD 90° – 60°= 30°
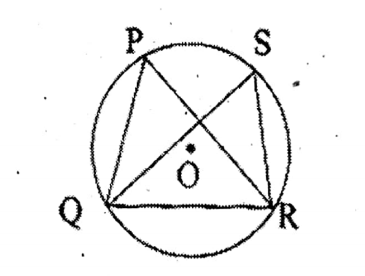
Question 2. In the adjoining figure, QS is the bisector of an angle /PQR, if SQR = 35° and ZPRQ 32°, let us find the value of ∠QSR.
Solution.
In the adjoining figure, QS is the bisector of an angle /PQR, if SQR = 35° and ∠PRQ 32°
∠SRP = SQR = ∠PSQ = 35°
∴∠QSR =∠QPR = 180° – (35° +35° + 32°) = 78°.
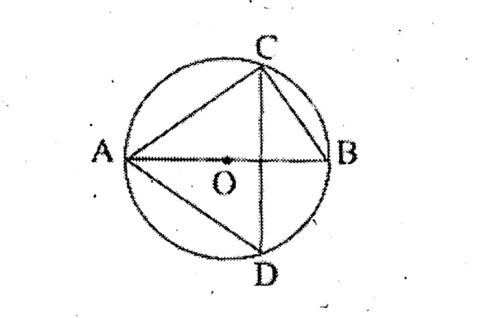
Question 3. In the adjoining figure, O is the center of the circle and AB is the diameter. If AB and CD are mutually perpendicular to each other and ZADC= 50°; let us find the value of CAD.
Solution:
In the adjoining figure, O is the center of the circle and AB is the diameter. If AB and CD are mutually perpendicular to each other and ZADC= 50°
BAD 90° = 50° = 40°
∴∠CAD = 2 x 40° = 80°.
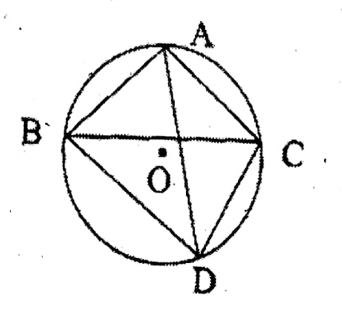
Question 4. In the adjoining figure, O is the center of the circle and AB = AC; if ZABC = 32°, let us find the value of BDC.
Solution:
In the adjoining figure, O is the center of the circle and AB = AC; if ZABC = 32°
∠ABC = ∠ACB = 32°
∴ BAC = 180° (32° 32°) = 116°
∠BDC = 180° – 116° = 64°
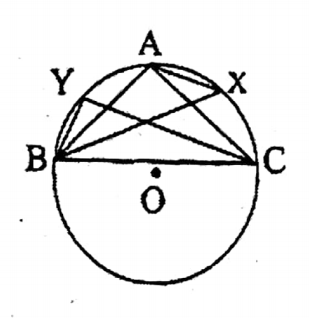
Question 5. In the adjoining figure, BX and CY are the bisectors of the angles ABC and ZACB respectively. If AB = AC and BY = 4 cm, let us find the length of AX.
Solution.
In the adjoining figure, BX and CY are the bisectors of the angles ABC and ZACB respectively. If AB = AC and BY = 4 cm
AX BY = 4 cm.
Question 6. Let us prove that the angle in the segment of a circle that is less than a semicircle is an obtuse angle.
Solution: In the figure, O is the center of the circle.
∴ The segment ACB is less than a semicircle.
To prove ∠ACB is an obtuse angle.
∴ ADB is a major arc.
In the reflex ∠AOB, the angle at the center standing on that arc is greater than 2 right angles.
∴ ∠ACB is an angle at the circle also standing on the same arc.
∠ACB is greater than 1 right angle.
∴ ∠ACB is an obtuse angle. Proved.
Question 7. Let us prove with the reason that the circle drawn with a hypotenuse of a right-angled triangle as diameter passes through the right angular vertex.
Solution: To prove that the circle drawn with BC as diameter passes through point A.
Proof: Let us suppose the circle does not pass through A. Then, let the circle intersects BA at point D.
∴∠BDC is 1 right angle ( angle in a semicircle is a right angle)
∴ BAC = 1 right angle (by hypothesis)
∴ <BAC = BDC.
This is impossible, if points D & A do not coincide,
since the exterior angle ∠BDC of Δ ADC > the interior
opposite angle ∠BAC.
∴ The circle passes through point A.