WBBSE Solutions For Class 10 Maths Chapter 8 Right Circular Cylinder Exercise 8.1
Question 1. If the length of the radius of the base of a right circular cylinder is 12 cm and the height is 21 cm, let us write by calculating its lateral surface area.
Solution:
Given
If the length of the radius of the base of a right circular cylinder is 12 cm and the height is 21 cm
The length of the radius of the cylinder is 12/2 cm = 6 cm.
∴The lateral surface area of a cylinder is = 2 x π x 6 x 21 sq cm.
= 2 x 22/7 x 6 x 21 sq cm.
= 792 sq cm.
The lateral surface area of a cylinder is 792 sq cm.
Read and Learn More WBBSE Solutions For Class 10 Maths
Question 2. The perimeter of a right circular cylinder is 44 meters and the height is 14 meters, let us write by calculating its lateral surface area.
Solution:
The perimeter of a right circular cylinder is 44 meters and the height is 14 meters
Surface area of the cylinder = circumference of base x height
= (44 x 14) sqm = 616 sqm.
Surface area of the cylinder = 616 sqm.
Question 3. The base area of a closed cylindrical water tank is 616 sq. meters and the height is 21 meters. Let us write by calculating the total surface area of that tank.
Solution:
Given
The base area of a closed cylindrical water tank is 616 sq. meters and the height is 21 meters.
Let the length of the radius of the circular base of the water tank = r meter.
∴ Base area = πr² sq meter
By the condition,
πr² = 616
or, 22/7 x r² = 616
or, r² = 616 7/22
r = √196
= 14
Total surface area of water tank is = (2лr² + 2лrh) sq meter [where height of cylinder = h meter]
= 2 x 22/7 x r(r + h) sq meter
= 2x 22/7 x 14(14+21) sq meter
= 3080 sqm.
Total surface area of water tank is 3080 sqm.
Question 4. If the perimeter of the base of any closed cylindrical pot is 22 dm and the height is 5 dm, let us write by calculating the area that will be colored to paint the outside of that pot.
Solution:
If the perimeter of the base of any closed cylindrical pot is 22 dm and the height is 5 dm
Let radius = r dm & height = h dm.
∴2πr = 22 &h=5
2 x 22/7 x r = 22.
r = 7/2 dm.
Question 5. The total surface area of a right circular cylinder with one end open is 1474 sq cm. If the length of the diameter of the base is 14 cm, let us write by calculating its height. Again, if the pot would be closed at two ends, let us write by calculating what would be its total surface area
Solution:
Given
The total surface area of a right circular cylinder with one end open is 1474 sq cm. If the length of the diameter of the base is 14 cm, let us write by calculating its height. Again, if the pot would be closed at two ends
The length of the radius of the base of the right circular cylindrical pot = 14/2 cm. = 7 cm.
Let the height of the pot is h cm.
∴The total surface area of pot = area of the base + area of the lateral surface
= (22/7×72+2 22/7 x 7 x h) sq cm.
= (154 + 44h) sq cm.
By the condition, 154 + 44h = 1474
∴ h = 30
∴ The height of the pot is 30 cm.
If the pot would be closed at two ends, the surface area of that pot
= Area of the upper end surface + 1474 sq cm.
22/7 x 72 + 1474) sq cm.
=.1628 sqcm.
Question 6. The length diameter of the base of a drum with a lid made of steel sheet is 4.2 dcm. If 112.20 sq dcm of steel sheet is required to make the drum, let us write by calculating the height of the drum. Again, if the price of 1 sq dcm of steel is Rs. 25, let us calculate the production cost of the drum.
Solution:
The length diameter of the base of a drum with a lid made of steel sheet is 4.2 dcm. If 112.20 sq dcm of steel sheet is required to make the drum, let us write by calculating the height of the drum. Again, if the price of 1 sq dcm of steel is Rs. 25
Let the height of the drum = h dcm.
The radius of the drum = 4.2/2 = 2.1 dcm.
According to the problem,
2.π x 2.1 (2.1+ h) = 112.20
or, 2x 22/7 x 22/7( 2.1+ h) = 112.20
(2.1+ h) = 1122x7x10 / 10×2×22×21
h 8.5 – 2.1 = 6.4 dcm.
Total surface area = 112.20 sq dcm = 1.1220 sqm.
Total cost Rs. 25 x 1.1220 = Rs. 28.05
Question 7. If the length of the diameter of the base of the glass is 11.2 cm and the height is 15 cm, let us calculate the volume of water that the glass will contain.
Solution:
If the length of the diameter of the base of the glass is 11.2 cm and the height is 15 cm
We understand, if the length of the diameter of the base of the glass is 11.2 cm, and the height is 15 cm, the glass will contain water
= π Χ (11.2/2)2 x 15 cubic cm.
=22/7 x 56/10 x 56/10 x 15
= 1478.4 sq cm.
The volume of water that the glass will contain = 1478.4 sq cm.
Question 8. The height of a right circular cylinder made of iron open at two ends is 42 cm. If the thickness of the cylinder is 1 cm and the length of its external diameter is 10 cm, let us calculate the volume of iron in it.
Solution:
Given
The height of a right circular cylinder made of iron open at two ends is 42 cm. If the thickness of the cylinder is 1 cm and the length of its external diameter is 10 cm
The length of the external radius of the cylinder = 10/2 cm. = 5 cm.
It is 1 cm in thickness.
Length of internal radius of the cylinder = (5-1) cm. = 4 cm. volume of iron
=22/7 (5²-4²) x 42 cubic cm.
= 2/7 x (5+4) (5-4) × 42 cubic cm.
[a²b² = (a + b) (a – b)]
=22/7 x 9 x 1 x 42 cubic cm.
= 22 x 9 x 6 cubic cm.
= 1188 cu cm.
Length of internal radius of the cylinder = 1188 cu cm.
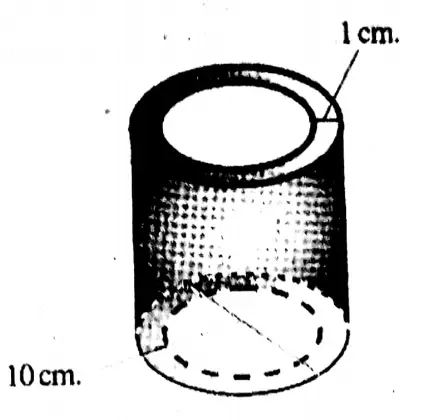
Question 9. If we color the inside and outside of the hollow right circular cylinder (Application 8) open at two ends, let us write by calculating how much area we shall color.
Solution: The sum of the inner and outer surface area of this hollow right circular cylinder open at two ends
=(2 ×π × 5 × 21+ 2x π x 4 x 21) sq cm.
= 2 × π x 21(5+4) sq cm.
= 2 x 22/7 x 21 x 9 sq cm.
= 1188 sq cm.
Question 10. If the inner and outer radii of a hollow right circular cylindrical pipe of 6 meter in length are 3.5 cm and 4.2 cm respectively, let us write by calculating the volume of the iron that the pipe contains. If I cubic decimetre of iron weighs 5 kilograms, let us write by calculating the weight of the pipe.
Solution:
If the inner and outer radii of a hollow right circular cylindrical pipe of 6 meter in length are 3.5 cm and 4.2 cm respectively, let us write by calculating the volume of the iron that the pipe contains. If I cubic decimetre of iron weighs 5 kilograms
Height of pipe = 6 m = 60 dcm.
Interval radius of pipe = 3.5/20 = 35/200 dcm.
The external radius of pipe = 4.2/20 = 42/100 dcm.
∴ Volume of Iron = π {(42/200)² – (35/200)² x 60} cu dcm.
= 22/7 x 77/200 x 7/200 x 60 cu dcm.
= 121 x 21 / 1000 cu dcm.
= 2541/ 1000 cu dcm.
= 2.541 cu dcm.
∴ Weight of 1 cu dcm of iron 5 kg.
∴ Weight of 2.541 cu dcm of iron = (2.541 x 5) kg
= 12.705 kg.
Question 11. If the area of the base of a cylinder is 13.86 sq meters and the height is 8 meters, let us calculate the volume of the cylinder.
Solution:
If the area of the base of a cylinder is 13.86 sq meters and the height is 8 meters
Let the length of the radius of the base of the cylinder is r. meter.
By the condition, πr²= 13.86
Or, 22/7 r² = 1386/100 x 7/22 = 441/100
∴r = 21/10 m.
∴The volume of the cylinder is 22/7 x 21/10 x 21/10 x 8 cubic meters
= 110.88 cu cm.
Question 12. If the perimeter of the base of a cylinder is 15.4 cm and the height is 10 cm, let us calculate its volume.
Solution: Let the radius of the base of the cylinder r cm & height = h cm = 10 cm.
∴Circumference = 2πr = 2 x 22/7 x r = 15.4
r = 154/10 x 7/2×22 = 49/20 cm.
∴The volume of cylinder πr2h
= 22/7 x 49/20 x 49/20 x 10 cu cm.
=3773/20
= 188.65 cu cm.
Question 13. If the glass of a tube light is 105 cm long and external circumference is 11 cm and it is 0.2 cm thick, let us write by calculating the volume (in cc) of the glass that will be required to make 5 such tube lights.
Solution: Let the length of external radius of tube light = r1 cm,
Length of internal radius = r2 cm and height is h cm.
By the condition,
External circumference is = 2r1 = 11 or,
\(r_1=\frac{11 \times 7}{2 \times 22}=\frac{7}{4}\)∴ The length of external radius is = \(\frac{7}{4}\) cm = 1.75 cm.
The glass of tube light is 0.2 cm thick.
∴ Length of internal radius of tubelight = r2
= (1.75 – 0.2)cm.
= 1.55 cm.
Question 14. Through a hole, 110 kiloliter of water enters a ship. After closing the hole a pump is connected for the drainage of water. If the length of the diameter of the pipe of the pump is 10 cm and the speed of water flow is 350 meters/minute, let us write by calculating the time that will be required by the pump to clear off all water in the ship.
Solution:
Through a hole, 110 kiloliter of water enters a ship. After closing the hole a pump is connected for the drainage of water. If the length of the diameter of the pipe of the pump is 10 cm and the speed of water flow is 350 meters/minute
The volume of water can be cleared off by the pump in 1 minute
=22/7 x 10/2 x 10/2 x1/100 x 3500 cubic dcm.
= 2750 cubic dcm = 2750 liters [1 cubic dcm. 1 liter.]
Time required to clear off 110 kilolitres of water =110000 / 2750
minutes 40 minutes.
So, the time required by the pump to clear off all water in the ship = is 40 minutes.
Question 15. A right circular cylindrical tank of 5 meters in height is fixed with water. Water comes out from there through a pipe having a length of diameter 8 cm at a speed of 225 meters/minute and the tank becomes empty after 45 minutes. Let us write by calculating the length of the diameter of the tank.
Solution:
A right circular cylindrical tank of 5 meters in height is fixed with water. Water comes out from there through a pipe having a length of diameter 8 cm at a speed of 225 meters/minute and the tank becomes empty after 45 minutes
Let the radius of the tank = r m.
∴Radius of pipe = 8/2 = 4 cm = 1/25 m.
∴ πr² x 5 = 45 x π (1/25)² X 225
5r² = 45×225 / 25×25
∴ r² = 45 x 1 x 9 / 5 x 25
=81/25
∴ r = 9/5 m.
∴Diameter of the tank = 2 x 9/5
= 18/5
3.6 m.
The length of the diameter of the tank is 3.6 m.