Chapter 5 Measurement Necessity Of Measurement In Our Daily Life
Measurement is the basis of science. In our daily life, we need to measure different things for different purposes.
See the following purposes:
- How far is your school from your house?
- When your school starts ?
- When your school close?
- How do you buy vegetables, fruits, rice, fish, etc. from the market?
- How do you buy packet milk, mustard oil or rice bran oil?
- How do you know that your friend has a fever?
- Which one is longer-door or the window of your study room?
- Which contains more milk-a cup of milk or a glass of milk?
- Which has a more area-your bedroom or your bathroom?
….. and so on.
Read and Learn More WBBSE Notes For Class 6 General Science and Environment
To answer all these questions, you need to measure something. Sometimes it may be the length, mass, time, volume, area, temperature, etc.
Now the question arises-how can you measure these things?
You need some instruments to measure length, time, etc.

For example, when we buy sugar or wheat, the grocer measures its mass (usually we call it weight) using a common balance. Sometimes an electronic balance is used for the same purpose for more accurate measurement.
When we fall sick, the doctor measures our body temperature by using a clinical thermometer.
Chapter 5 Measurement Physical Quantities
Anything that can be measured with certain instruments is called a physical quantity. Some of examples of physical quantities are length, breadth, height, area, volume, mass, weight, density, time, temperature, etc.
The number of physical quantities that can be measured are very large. All physical quantities are classified as fundamental and derived quantities.
| Class 6 History | Class 6 Social Science |
| Class 6 Geography | Class 6 Science |
| Class 6 Maths | Class 6 Science MCQs |
| Class 6 General Science | Class 6 Maths Solutions |
| Class 6 Geography | Class 6 Hindi |
Fundamental and Derived quantities :
Suppose you want to measure the floor area of your study room. Using a measuring tape, you will record the ‘length’ and ‘breadth’ of the floor and then multiply these two to get the actual floor area, i.e., Area = length and breadth.
Again, if you want to measure the volume of the room, by the same way you are to record the ‘height’ of the room and use the formula Volume = length x breadth x height.
Note that, while measuring ‘area’ you used the physical quantity ‘length’ for twice and while measuring ‘volume’ the physical quantity ‘length’ is used thrice.
“WBBSE Class 6 General Science Chapter 5 measurement solutions”
So, you understand that the physical quantity ‘length’ does not depend on other quantities whereas area, volume or density (Density = mass + volume) depend on other physical quantities.
Definition:
The physical quantities which do not depend on other quantities (i.e. which cannot be simplified further) are called fundamental quantities. Length, mass and time are examples of fundamental quantities.
The physical quantities which are expressed in terms of two or more fundamental quantities are called derived quantities. Area, volume, density, speed, force, momentum, etc. are examples of derived quantities.

Chapter 5 Measurement Units Of Measurement
All measurements are based on the comparison.
How?
Usually, the thing which to be measured is compared with a known constant quantity of the same nature as a ‘standard’. This standard quantity is nothing but a standard unit. Let us try to understand the meaning of this statement.
“WBBSE solutions for Class 6 Science measurement chapter”
Earlier, to measure the length the ancient men used various kinds of standards such as a footstep (a pace), an arms length (a cubit), a hand span, a foot or width of four fingers, etc.
Suppose, you measure the length of your study room with the help of your foot. If it is equal to twenty feet, you may say that the length of your study room is equal to twenty foots.
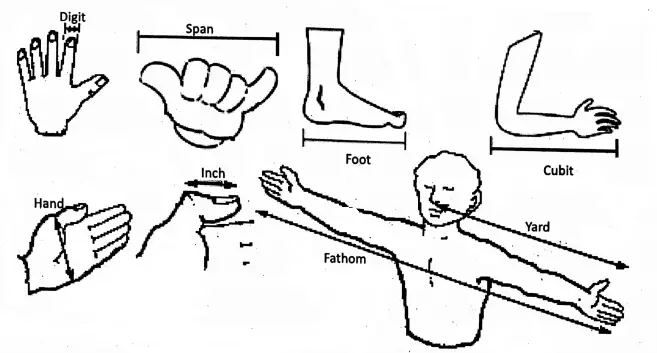
In this case, the foot is taken as the unit of length and twenty is the numerical value of the measurement. See the following where some earlier units of measurement of length are shown.
However, all these units vary from person to person and led to a lot of confusion.
You see that any measurement involves two things:
A number and a unit. No measurement is complete unless both the number and the unit are mentioned.
For example:
If your height is 1.5 metres, then 1-5 is the number and the metre is the standard unit. Your mass of 45 kg means that your mass is 45 times the standard mass of 1 kg. Here 45 is the number and kg is the standard unit.
“Class 6 WBBSE General Science Chapter 5 measurement exercises”
So, if we say that the mass of a body is 20-it is totally meaningless, rather we are to say 20 grams or 10 kilograms.
What is a unit?
Unit:
For the measurement of any physical quantity, some convenient and definite quantity of the same nature is chosen as a standard and the physical quantity is expressed by a numerical value to represent how many times the standard quantity is contained in the given physical quantity.
This standard quantity is called a standard unit. The units used to measure fundamental quantities such as length, mass, time are called fundamental units and the units used to measure derived quantities like area, volume, density, etc. are called derived units.
Chapter 5 Measurement System Of Units
In ancient days, different systems of units were used. In France in 1791, the metric system for standard units was first adopted. In this system, metre-kilogram-second (MKS) were taken as the base units.
Of length, mass and time respectively; And for measuring smaller physical quantities centimetre-gram-second (CGS) were taken as the base units of length, mass and time respectively.
To make measurement more scientific, convenient and uniform, scientists accepted a system of units called the SI units or International system of units in the year 1960.
It is used in science and technology all over the world in a uniform pattern. In this system, there are seven fundamental quantities.
| Physical Quantity | Unit | Symbol |
| Length | metre | m |
| Mass | kilogram | kg |
| Time | second | s |
| Electric current | ampere | A |
| Temperature | kelvin | K |
| Intensity of light | candela | cd |
| Amount of substance | mole | mol |
Multiples And Sub Multiples Of Metres
It is the fact that for the measurement of long lengths or distances, we require larger units of metre and for measuring smaller lengths, we require smaller units of the metre. For example, the distance from Howrah to Puri is 499000 m or 499 thousand metres.
To express such a long distance in metres is not practical. Therefore to measure larger lengths, we need different multiples of metres. Similarly, to measure the length of a small object like a pencil, pen or eraser, the metre is too big.
“Step-by-step solutions for measurement Class 6 WBBSE”
Therefore, to measure lengths smaller than a metre we need different sub-multiples (or fractions) of the metre. And see the tables.
Multiples of metre
| Multiples | Symbol | Relation |
| 1 decametre | dam | 10 metre |
| 1 hectometre | hm | 100 metre |
| 1 kilometre | km | 1000 metre |
Sub-multiples of metre
| Sub-multiples | Symbol | Relation |
| 1 decimetre | dm | 1/100 metre |
| 1 centimetre | cm | 1/100 metre |
| 1 millimetre | mm | 1/1000 metre |
Chapter 5 Measurement Measurement Of Different Physical Quantities
Measure of length
In general, the shortest distance between two ends of an object is called its length. Breadth, depth, height, thickness, radius, diameter, etc. are different physical quantities but all these are lengths.
The practical units of length are metre, centimetre, inch, foot, etc. for everyday use.
Definition of international standard metre:
A cylindrical bar made of an alloy of platinum (90%) and iridium (10%) was kept at the International Bureau of Weights and Measures in Paris, France.
The distance between two fine marks engraved on the platinum-iridium bar maintained at 0°C (or.273K) temperature is called the International Prototype of a metre.
“Step-by-step solutions for measurement Class 6 WBBSE”
You know that 1 centimetre = 1/100th part of 1 metre
1 inch (symbol”) = 2.54 centimetre
1 foot (symbol) = 12 inches or 0.3048 cm
Common instruments we use to measure length are rulers, metre scales and measuring tapes. Look at your ruler (15 cm long) and find that it is marked with centimetres on one side and inches on the other side.

To measure the length of a pencil, the zero mark of the scale is made to coincide with one of the ends of the pencil and the scale reading coinciding with the other end of the block is taken.
To reduce error in this measurement, the eye must be positioned at vertically above the point whose measurement is to be taken.
Measurement Of Area
In general, area means the space occupied by a flat shape or the surface of an object. Its SI unit is m2.
Suppose you are asked to measure the area of your science book. Place the book on a table and measure its length and breadth with an ordinary scale and then apply the formula: Area = length and breadth.
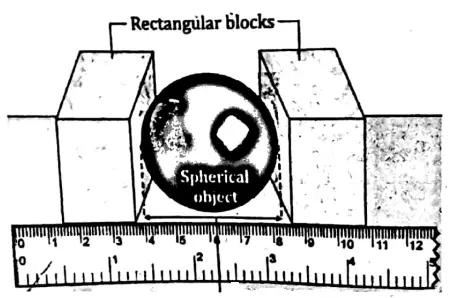
If you are said to measure the area of a spherical object like a football, you are to measure its diameter first. and like this, held the sphere in between two books or rectangular blocks.
Measure the distance between the inner edges of the blocks by an ordinary scale. This distance is the diameter of the sphere. Then apply the formula: Area = π × diameter x diameter. [π (pi) is a constant number whose value is 22/7 or 3.14].
The SI unit of area is square metre (symbol m2) where 1 m2 = 1 m x 1m = 100 cm x 100 cm = 10,000 cm2.
Measurement Of Volume
In general, volume is the quantity of space occupied by the closed surface of any shape of a substance (solid, liquid or gas). Its SI unit is cubic metre or m3 where 1m3= 1m x 1m x 1 m = 100 cm x 100 cm x 100 cm = 1000000 cm3.
If the length, breadth and height of a cube are of 1 m then the volume of the cube will be 1 m3. The volume of a liquid is expressed by the unit litre (symbol L).
Sometimes smaller unit of litre like millilitre (symbol ml) is used where 1 litre = 1000 millilitre.
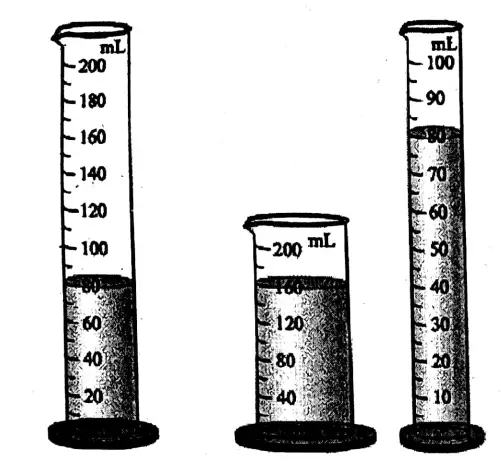
There are different instruments used to measure the volume of a liquid. A measuring cylinder is one of these. In the three measuring cylinders of different sizes (or volumes) are shown. They are graduated in ml from bottom to upwards.
Measuring cylinders are made of glass or plastic and availability of different sizes such as 50 ml, 100 ml, 200 ml, etc.
“WBBSE Class 6 General Science Chapter 5 important questions and answers”
Suppose you are said to measure the volume of tea in a cup or some milk, you are to pour the total amount of that liquid into an empty measuring cylinder.
Take the scale reading where the uppermost surface of the liquid touches the measuring cylinder. This is how you can know the required volume of some liquid.
Measurement Of Time
What is the meaning of ‘time’?
‘Time’
The interval between any two instances (or incidents or events) is called ‘time’.
If you are asked to say what is the time duration of your tiffin break?
Here, two events are the ‘starting of tiffin break’ and the ‘ending of tiffin break’. The interval between these two events is the actual required time.
The standard unit of time is second (s). It is actually measured in terms of a mean solar day. A mean solar day is a time taken by the earth to complete one rotation about its own axis. Its value is 24 hours.
That is, 1 mean solar day = 24 hours (24 x 60 x 60) seconds = 86400 s
Thus, 1s = 1/86400 part of 1 mean solar day
To measure the time of larger events, larger units like minutes, hours, days, months, years, decades, and centuries are used. For example, you express your age in years, months and days.
1 min = 60s
1h = 60 min
1 day = 24 h
1 year = 365¼ days
1 leap year = 366 days.
1 decade = 10 years
1 century = 10 decades
How To Measure Time
The instrument used to measure time is a clock or watch. The earlier people used to estimate time by looking at the visible position of the sun in the sky.
Then came the early clocks like sundial clocks, sand clocks, simple water clocks, etc. (see the shown below). The sundial clock has a flat plate called the dial and a metal rod which casts a shadow on the dial at different hour lines when the sun appears to move at different positions in the sky.

Nowadays, time is measured with the help of modern advanced clocks and watches like pendulum clocks, table clocks, wristwatches, digital clocks, stopwatches, modern atomic (quartz) clocks, etc.
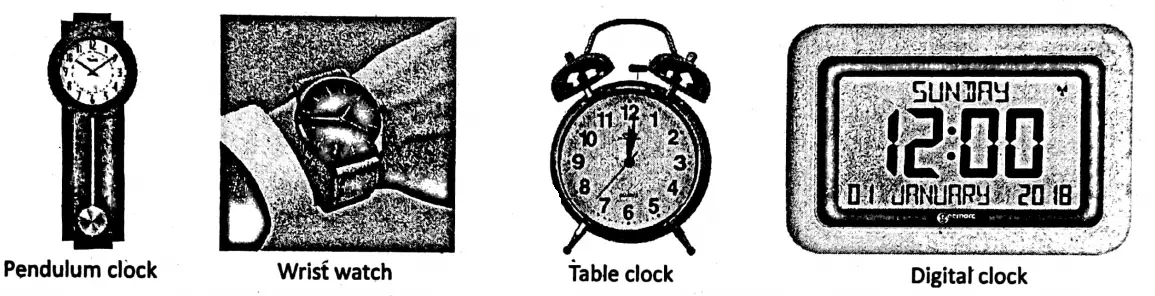
Our watches record time in seconds, minutes and hours. The minimum time it can measure is one second, i.e., by it less than a second cannot be measured. But in certain activities, there is a need to measure even a 1/100th fraction of a second accurately.
A digital clock is used for such purposes. For example, to measure the time taken by an athlete to finish a 100-metre race, the knob is to be pressed at the starting point and then at the finishing point.

The time interval gives the accurate time in seconds. For re-use, the knob is to be pressed once again to bring both the minute’s hand and the second’s hand to the initial position.
Stopwatch can measure 1/10th of a second accurately. Nowadays digital stopwatch is preferably used as it can measure 1/100th of a second.
Measurement Of Mass
The mass of a body is the amount of material substance contained in it. It can be measured by using a beam balance or physical balance. To measure the mass of rice, wheat, pulses, sugar and others, a shopkeeper usually uses standard weights like 1 kg, 500 g, 100 g, 50 g, etc.
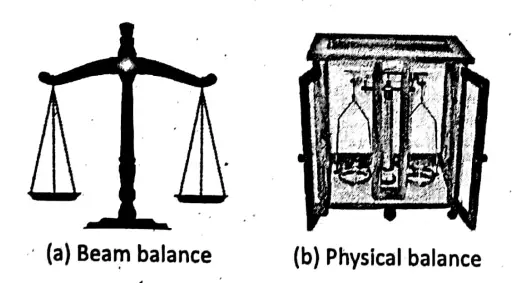
The body whose mass is to be measured is placed on the left pan and standard weights are placed on the right pan till the beam comes in a horizontal position.
To measure small masses to a precision of 1 mg or even less, a physical balance is mainly used in laboratories and in jeweller shops.
Chapter 5 Measurement Importance Of Estimation In Measurement
In our daily activities, we do not always do work with accurate measurements using instruments. In cases where actual measurement is practically not possible, we often make estimations or approximations.
For example:
- We add sugar to a cup of tea by estimation only.
- You may take 10 minutes to reach your school by walking. If you walk fast, you may take 9 minutes or if there is a jam on the road, the time maybe 11 minutes.
- For cooking food, if the amount of salt is slightly less or more, it does not make much difference.
- When we buy vegetables or groceries, the measurement may not be accurate. But when we buy gold, the measurement should be precise.
Note: Estimation is a skill that one learns by practice.
However, while dealing with some devices like computers, rockets, etc. accurate measurement of various parameters is a must. The errors that come in readings can be reduced by taking the average of a large number of measurements of the same quantity.
Measurement Of Plant Growth
You must know that plant growth means the process by which a plant grows in size. Apparently simply by looking you can estimate about the growth of a plant but to know the actual growth you must need an apparatus.
An auxanometer or arc-auxanometer is such an apparatus. See shown alongside. In this apparatus, there is a flexible wire attached with the plant apex at one end and a weight attached at its other end.
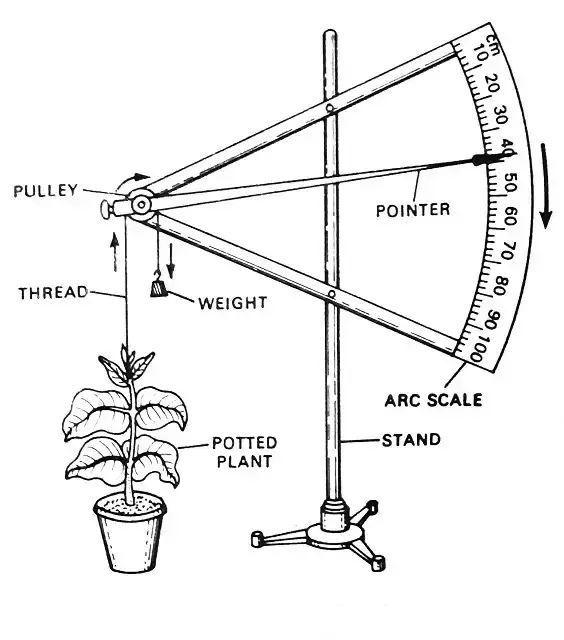
This wire passes over a pulley or a wheel. A pointer (or indicator) is attached with this wire. The pointed end of the indicator lies on a scale like an arc of a circle.
“Solved examples of measurement WBBSE Class 6 Science”
The indicator initially rests at ‘0’. When the height of the plant increases, the pulley rotates and accordingly the indicator moves over the scale. The scale reading gives the magnitude of plant growth over a certain period of time.
The rate of plant growth can be calculated by diving the increase in plant height by time.
Measurement Of Animal Growth
Using a centimetre scale we can measure the growth of man and other animals. In your physical education class, you must have seen the centimetre scale.
You are to stand straight in front of it and you are to note the point where your head touches the indicator. This length gives the measurement of your height in centimetres.
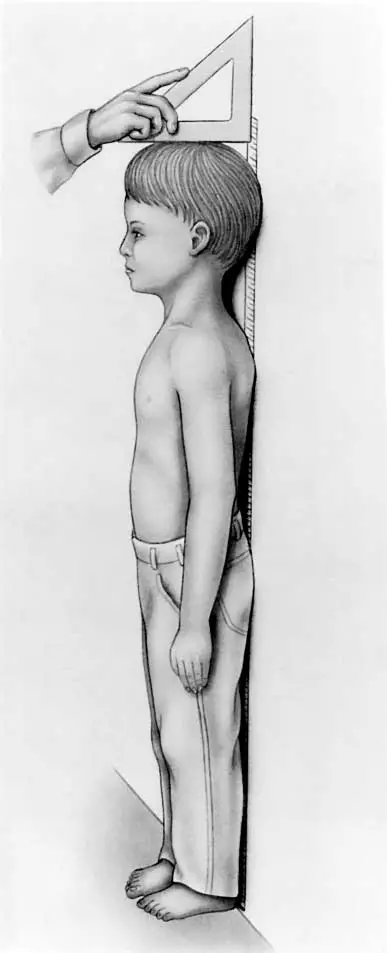
To measure the average height of all students in your class measure the height of all. Add all the values. Divide the total height by the number of students. You will get the average height of the students in your class.
“Best guide for Class 6 General Science WBBSE measurement chapter”
You can also find which height is maximum and which height is minimum. Taking the difference of these two values, you can also find the range of height of the students in your class.
WBBSE Notes For Class 6 General Science and Environment
-
- Chapter 1 Interdependence of Organisms and the Environment
- Chapter 2 Phenomena Around Us
- Chapter 3 Element, Compound and Mixture
- Chapter 4 Rocks and Minerals
- Chapter 5 Measurement
- Chapter 6 Primary Concept of Force and Energy
- Chapter 7 Statics and Dynamics of Fluid
- Chapter 8 The Human BodyChapter 9 Common Machines
- Chapter 10 Biodiversity and its Classification
- Chapter 11 Habits and Habitats of Some Important Animals
- Chapter 12 Waste Products
