Class 6 Math Solutions WBBSE Chapter 12 HCF And LCM Of Three Numbers Exercise 12
Question 1. Let’s find the greatest number which will divide both 564 and 630 to keep the remainder 3 in both cases.
Solution:
⇒ 564 – 3 = 561
⇒ and 630-3 = 627
∴ The greatest number is the H.C.F. of 561 and 627.
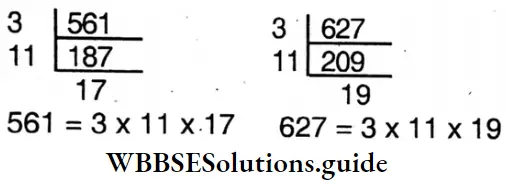
∴ H.C.F. = 3 x 11 =33
“WBBSE Class 6 Maths Chapter 12 HCF and LCM solutions”
Question 2. Let’s find the greatest number which divides 78,182 and 195 and keeps number remainder.
Solution: 78; 182; 195

∴ Required H.C.F = 13
Read and Learn More WBBSE Solutions For Class 6 Maths
Question 3. Mill bought a few exercise books for Rs. 80.50 p. Her brother bought a few more for Rs. 57.50 paise. Let’s find the maximum price of an exercise book and the total number of exercise books bought.
Solution:
Given
Mill bought a few exercise books for Rs. 80.50 p. Her brother bought a few more for Rs. 57.50 paise.
⇒ Rs. 80.50 = 8050 p
⇒ Rs. 57.50 = 5750 p
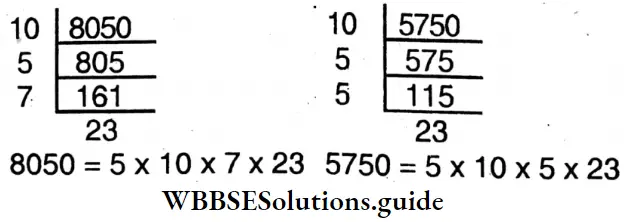
∴ H.C.F. = 5x 10 x 23 = 1150
∴ Maximum price of an exercise book = 1150 p.
⇒ Total Amount = (8050 + 5750) p = 13800 p.
∴ Number of exercise books = 13800/1150 = 12
Class 6 WBBSE Math Solutions Chapter 12 HCF And LCM Of Three Numbers Exercise 12.1
Question 1. Four bells ring at an interval of 45 min, 1 hour, 1 hr 15 min, and 1 hr 30 m. Let’s find bells ringing together at 12, when will these ring together again? Also, let’s find out how many times the bells will separately ring during these hours.
Solution:
Class 6 Math Solutions WBBSE
Given
Four bells ring at an interval of 45 min, 1 hour, 1 hr 15 min, and 1 hr 30 m.
⇒ 45 min = 45 mins
⇒ 1 hour = 60 mins
⇒ 1 hr 15 mins = 75 mins
⇒ 1 hr 30 mins = 90 mins
⇒ L.C.M. of 45,60,75, 90
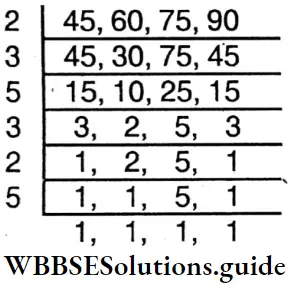
∴ Required L.C.M =2x3x5x3x2x5 = 900 mins = 15hrs.
⇒ The bells ring together at 12 room, then again the bells will ring together at 12 noon + 15 hrs. = 3 A.M.
⇒ Number of times 1st bell rings separately = 900 ÷ 45 = 20
⇒ Number of times 2nd bell rings separately = 900 ÷ 60 = 15
| Class 6 History | Class 6 Social Science |
| Class 6 Geography | Class 6 Science |
| Class 6 Maths | Class 6 Science MCQs |
| Class 6 General Science | Class 6 Maths Solutions |
| Class 6 Geography | Class 6 Hindi |
⇒ Number of times 3rd bell rings separately = 900 ÷ 75 = 12
⇒ Number of times 3rd bell rings separately = 900 ÷ 90 = 10
“WBBSE solutions for Class 6 Maths HCF and LCM of three numbers”
Question 2. Let’s work to find the least number of four digits which will be divisible by 12,15, 20, and 35.
Solution:
L.C.M. of 12,15, 20 and 35

= 2x2x3x5x7 = 420
⇒ Least number of 4 digits, divisible by 12,15, 20, and 35 is = 420 x 3 = 1260.
Question 3. Let’s work out to find the greatest number of five digits which when divided by 16, 24, 30 and 36 will leave a remainder 10 in each case.
Solution:
L.C.M. of 16, 24, 30 and 36

= 2x2x3x2x5x3x1 = 720
⇒ Greatest number of five digits = 99999
Class 6 WBBSE Math Solutions

∴ The required number = (99999 – 639) + 10
= 99360 + 10 = 99370.
“How to find HCF and LCM of three numbers Class 6 WBBSE”
WBBSE Math Solutions Class 6 Chapter 12 HCF And LCM Of Three Numbers Exercise 12.2
Question 1. There are three small tanks of capacity 35 liters, 56 liters, and 84 liters. Let’s find what will be the biggest capacity of a container that will measure the oil of the 3 tanks in exact whole numbers.
Solution:
Given
There are three small tanks of capacity 35 liters, 56 liters, and 84 liters.
⇒ To find the biggest capacity of a container we have to find the H.C.F. of 35 litres, 56 litres, and 84 litres

∴ The biggest capacity of the container = 7 litres.
Question 2. The length and breadth of our school hall are 2000 cm and 1600 cm respectively. Let s find the length of the longest tape which can measure both length and breadth in exact whole numbers.
Solution:
Given
The length and breadth of our school hall are 2000 cm and 1600 cm respectively.
⇒ To find the longest tape to measure 2000 cm and 1600 cm we have to find the H.C.F. of 2000 and 1600 cm.
⇒ 2000 cm = 20 m.
⇒ 1600 cm = 16 m.
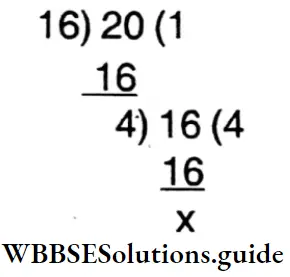
∴ Length of the tape = 4 m.
“Class 6 Maths WBBSE Chapter 12 HCF and LCM exercises”
Question 3. There is a stock of 1071 dhotis, 595 sarees, and 357 dresses. Let us calculate the maximum number of families among which these can be distributed equally. How many of these things will each family receive?
Solution:
Given
There is a stock of 1071 dhotis, 595 sarees, and 357 dresses.
⇒ Number of dhotis = 1071
⇒ Number of sarees = 595
⇒ Number of dresses = 357
WBBSE Math Solutions Class 6
Now find H.C.F. of 1071,595,357 357,595, 357

⇒ Number of Dhotis = \(\frac{1071}{119}=9\)
⇒ Number of Sarees = \(\frac{595}{119}=5\)
⇒ Number of Dresses = \(\frac{357}{119}=3\)
∴ Maximum number of families = 119.
“Step-by-step solutions for HCF and LCM Class 6 WBBSE”
Question 4. The perimeter of the front wheel of an engine is 1 m 4 dcm and the perimeter of its hind wheel is two and a half times more than the front wheel. Let’s find the least distance covered by the wheels when they will simultaneously take an exact number of complete revolutions.
Solution:
Given
The perimeter of the front wheel of an engine is 1 m 4 dcm and the perimeter of its hind wheel is two and a half times more than the front wheel.
⇒ The perimeter of the front wheel = 1 m 4 dcm = 14 dcm
⇒ and the perimeter of its hind wheel = 14 x 2\(\frac{1}{2}\)
= 14 x \(\frac{5}{2}\) dcm.
= 35 dcm.
⇒ Now, H.C.F. of 14 dcm and 35 dcm = 7 dcm.
∴ Least distance covered by the wheels = 7 dcm.
Question 5. Let’s find the H.C.F. of the following numbers,
- 24, 36, 54
- 24, 30, 40, 48
- 296, 703, 814
- 160,165, 305
- 165,264,286
- 906,1510,1057
Solution:
1. 24, 30, 40, 48
Solution:
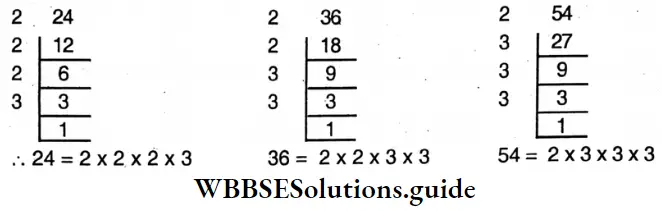
∴ H.C.F. = 2×3 = 6
2. 24, 30, 40, 48
Solution:

⇒ H.C.F. of 24, 30,40, 48
⇒ 24 = 2 x 2 x 2 x 3.
⇒ 30 = 2 x 3 x 5
⇒ 40 = 2 x 2 x 2 x 5
⇒ 48 = 2 x 2 x 2 x 2 x 3
∴ H.C.F. = 2

“WBBSE Class 6 Maths Chapter 12 important questions and answers”
3. 296,703,814
Solution:
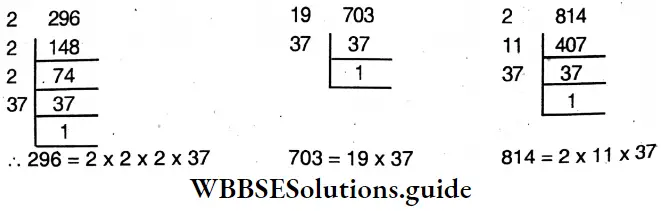
H.C.F. of 296, 703, 814
∴ Required H.C.F. = 37
4. 160,165, 305
Solution:

⇒ H.C.F. of 160, 165, 305
∴ H.C.F. = 5
WBBSE Class 6 Maths Solutions
5. 165, 264, 286
Solution:
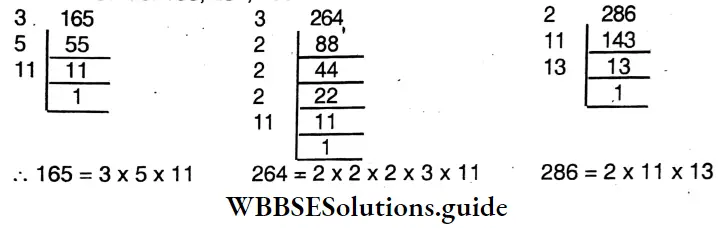
⇒ H.C.F. of 165, 264, 286
∴ H.C.F. = 11
“Solved examples of HCF and LCM of three numbers WBBSE Class 6”
6. 906, 1510, 1057
Solution:
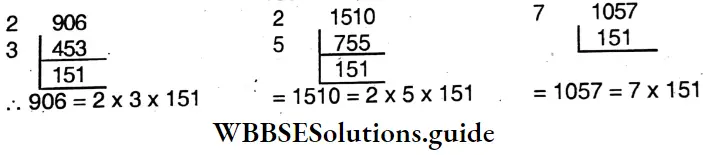
⇒ H.C.F. of 906, 1510, 1057
∴ Required H.C.F. = 151
Question 6. Let’s find the greatest number which divides 306,810 and 2214 and keeps the number remainder.
Solution:
⇒ To find the required greatest number we have to find the H.C.F. of 306, 810, and 2214.

∴ H.C.F. = 18.
∴ The required number = 18.
Question 7. The traffic signal lights at three different crossings of a road change at every 16 seconds, 28 sec, and 40 sec respectively. If the signal lights changed together at 8 a.m in the morning, let’s find when the three signal lights will change together again.
Solution:
Given
The traffic signal lights at three different crossings of a road change at every 16 seconds, 28 sec, and 40 sec respectively. If the signal lights changed together at 8 a.m in the morning,
L.C.M. of 16 sec, 28 sec, and 40 sec

∴ L.C.M = 2x2x2x2x7x5 = 560 sec = 9 mins 20 sec.
⇒ The three signal lights will change together 9 min 20 sec after 8 am, i.e., 8 hr 9 min 20 sec.
Question 8. There are three sticks in our house of lengths 45 cm, 50 cm, and 75 cm. Let’s find the least length of a tape which can be completely measured by each stick.
Solution:
Given
There are three sticks in our house of lengths 45 cm, 50 cm, and 75 cm.
⇒ To find the required length of the tape we have to find the LC.M. of 45,50, and 75.
Class 6 Math WBBSE Solutions
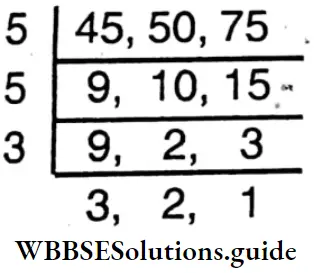
⇒ L.C.M. = 5x5x 3x3x2 = 450
∴ The least length of the tape = 450 cm.
Question 9. Let’s find the least number which is divisible by 15,20,24 and 32.
Solution:
The least number is the L.C.M. of 15, 20, 24, and 32.

∴ L.C.M. = 2x2x2x3x5x4 = 480
“Best guide for HCF and LCM of three numbers Class 6 WBBSE”
Question 10. Let’s find the L.C.M. of the following:
- 36, 60, 72
- 24, 36, 45, 60
- 105,119,289
- 144,180, 348
- 110,165, 330
- 204, 408, 306
Solution:
Class 6 Math WBBSE Solutions
1. 36, 60,72
Solution:
L.C.M. of 36, 60, 72

∴ L.C.M. = 2x2x3 x 3x5x2 = 360
2. 24, 36, 45, 60
Solution:
L.C.M. of 24, 36, 45, 60

∴ L.C.M. = 2x2x3x3x5x2 = 360
3. 105,119,289
Solution:
Class 6 Math WBBSE Solutions
⇒ L.C.M. of 105,119, 289
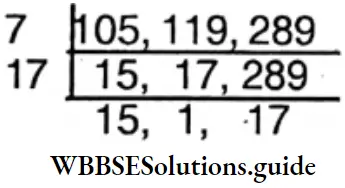
∴ L.C.M. = 7x 17 15 x 17 = 30345
4. 144,180, 348
Solution:
⇒ L.C.M of 144,180, 348

∴ L.C.M. = 2x2x3x3x4x5x29 = 20880
5. 110, 165, 330
Solution:
⇒ L.C.M Of 110, 165, 330

⇒ L.C.M = 2x2x3x3x4x5x29 = 20880
6. 204, 408, 306
Solution:
WBBSE Class 6 Maths Solutions
⇒ L.C.M of 204, 408, 306

⇒ L.C.M = 2x2x3x17x2x3 = 1224
Question 11. Let’s find the H.C.F. and the L.C.M. of the following.
1. 6 Rs. 50 paise, 5 Rs. 20 paise and 7 Rs. 80 paise.
Solution:
⇒ Rs. 6, 50p = 650p
⇒ Rs. 5, 20p = 520p
⇒ Rs. 7, 80p = 780p
⇒ H.C.F.
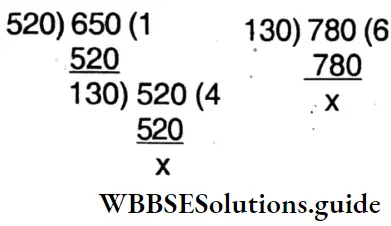
⇒ H.C.F. = 130p = Rs. 1 30p
⇒ L.C.M.

L.C.M. = 2x2x3x5x10x13 = 7800p = Rs. 78.
2. 2 m 28 cm, 3 m 42 cm, 4 m 56 cm.
Solution:
WBBSE Class 6 Maths Solutions
⇒ 2 m 28 cm. = 228 cm.
⇒ 3 m 42 cm = 342 cm.
⇒ 56 cm = 456 cm.
⇒ H.C.F
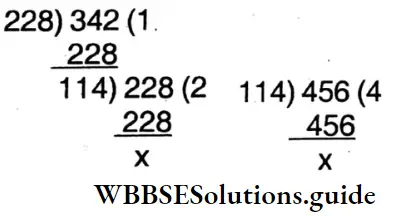
⇒ H.C.M. = 114 cm
= 1 m 14 cm
L.C.M

L.C.M = 2 x 2 x 2 x 3 x 3 x 1 9 = 1 368 cm
= 13 m 68 cm
3. 3 I 600 ml, 4 I 800 ml, 6 I.
Solution:
⇒ 3 litre 600 ml = 3600 ml
⇒ 4 litre 800 ml = 4800 ml
⇒ 6 litre = 6000 ml
WBBSE Class 6 Maths Solutions
H.C.F
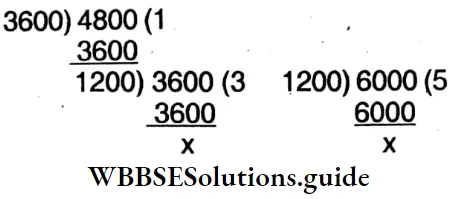
⇒ H.C.F. = 1200 ml.
= 1 litre 200 ml
L.C.M

L.C.M. = 2 x 2 x 3 x 3 x 3 x 4 x 5 x 100 = 72000 ml.
= 72 litre,
4. 6 hours 4 min 30 sec, 2 hours 42 min.
Solution:
⇒ 6 hr, 4 min 30 sec – (6 x 3600 + 4 x 60 + 30) secting
= 21600 + 240 + 30 sec = 21870 sec
⇒ 2 hr 42 min = (2 x 60 + 42) = 162 min
= 162 x 60 sec
WBBSE Class 6 Maths Solutions
H.C.F

H.C.F.= 9720 sec
L.C.M

L.C.M = 9 x 9 x 3 x 4 x 9 x 10
= 87480 sec
= 1458 min
= 24 hr 18 min
Question 12. From the pairs of numbers given below, let’s find if the product of two numbers is equal to the product of their H.C.F and L.C.M
1. 87,145
Solution:
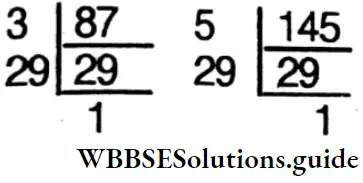
⇒ 147 = 5×29
⇒ L.C.M = 3 x 5 x 29 = 435
∴ Product of the two numbers = 87 x 145 = 12615
⇒ Product of their H.C.F. x L.C.M. = 29 x 435 = 12615
∴ Product of the two numbers = Product of their H.C.F. x L.C.M.
2. 60, 75
Solution:

⇒ 60 = 2x2x3x5
⇒ 75 = 3 x 5 x 5
⇒ H.C.F = 3×5 = 15
⇒ L.C.M = 2x2x3x5x5 = 300
⇒ Product of the two numbers = 60 x 75 = 4500
⇒ Product of their H.C.F. x L.C.M. = 15 x 300 = 4500
∴ Product of the two numbers = Product of their H.C.F. x L.C.M.
3. 42, 63
Solution:
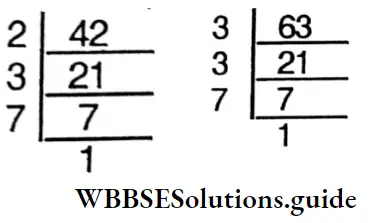
⇒ 42 = 2 x 3 x 7
⇒ 63 = 3x3x7
∴ H.C.F. = 3×7 = 21
⇒ L.C.M. = 2x3x3x7 = 126
⇒ Product of the two numbers = 42 x 63 = 2646
Class 6 WBBSE Math Solutions
⇒ Product of their H.C.F. and L.C.M. = 21 x 126 = 2646
⇒ Product of the two numbers = Product of their H.C.F. and L.C.M.
4. 186, 403
Solution:
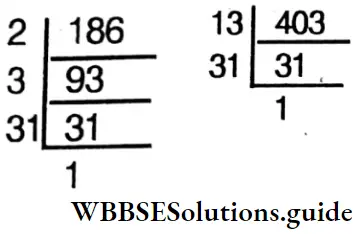
⇒ 186 = 2x3x31
⇒ 403= 13×31
⇒ H.C.F. = 31
⇒ L.C.M. = 2x3x13x31 =2418
⇒ Product of the two numbers = 186 x 403 = 74958
⇒ Product of their H.C.F. and L.C.M. = 74958
∴ Product of the two numbers = Product of their H.C.F. and L.C.M.
Question 13. The L.C.M. and H.C.F. of the two numbers are 2175 and 145 respectively. If one number is 725, let’s find the other number.
Solution:
Given
The L.C.M. and H.C.F. of the two numbers are 2175 and 145 respectively. If one number is 725
⇒ L.C.M. = 2175
⇒ H.C.F. = 145
∴ Product of the two numbers = Product of L.C.M. and H.C.F. = 2175 x 145
⇒ One number = 725
∴ Other number = \(\frac{2175 \times 145}{725}=435\)
Question 14. Let’s find the H.C.F. of 145 and 232. Using H.C.F. let us find L.C.M.
Solution:
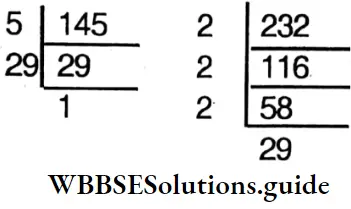
⇒ 145 = 5×29
⇒ 232 = 2 x 2 x 2 x 29
∴ H.C.F. = 29
∴ H.C.F. x L.C.M. = Product of two numbers
∴ 29 x L.C.M. = 145×232
∴ L.C.M = \(\frac{145 \times 232}{29}=1160\)
∴ L.C.M. = 1160
Class 6 WBBSE Math Solutions
Question 15. Let’s find the L.C.M of 144 and 384. Using L.C.M let’s find their H.C.F.
Solution:

⇒ 144 = 2x2x2x2x3x3
⇒ 384 = 2x2x2x2x2x2x2x3
∴ L.C.M = 2x2x2x2x2x2x2x3x3 = 1152
⇒ H.C.F x L.C.M = Product of two numbers
∴ H.C.F x 1152 = 144×384
⇒ HCF = \(\frac{144 \times 384}{1152}=48\) = 48
∴ H.C.F = 48
Question 16. Find the least number that must be subtracted from 5834, so that the result is divisible by 20, 28, 32, and 35.
Solution:

⇒ L.C.M. = 2x2x5x7x8 = 1120
∴ The required least number = 234
Class 6 WBBSE Math Solutions
Question 17. Let’s find the greatest number which divides 2300 and 3500 to leave the remaining 32 and 56 respectively.
Solution:
⇒ The required number is the H.C.F. of (2300 – 32) = 2268 and (3500 – 56) = 3444

⇒ H.C.F. = 84
∴ Required greatest number = 84
Question 18. Let’s find the greatest number that divides 650, 775 and 1250 to keep equal remainder in all cases.
Solution:

⇒ H.C.F. = 25
∴ Required greatest number = 25
Question 19. The sum of two numbers is 384 and their H.C.F. is 48, what may be the 2 possible numbers?
Solution:
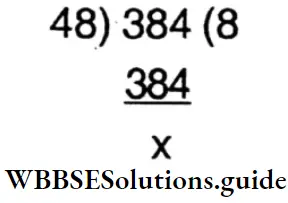
8 = 1+7……..(1)
= 2 + 6 …….(2)
= 3 + 5 …….(3)
= 4 + 4 …….(4)
⇒ In 1st case, the numbers are (48 x 1) and (48 x 7) = 48, 336.
⇒ In 2nd case, the numbers are (48 x 2) and (48 x 6) = 96, 288.
⇒ But it is not possible as the H.C.F of 96 and 288 is 96.
⇒ In 3rd case, the numbers are (48 x 3) and (48 x 5) = 144, 240.
⇒ In 4th case, the numbers are (48 x 4) and (48 x 4) = 192, 192.
⇒ But it is not possible as the H.C.F of 192 and 192 is 192.
.-. Required numbers are (48, 336) and (144,240).
Question 20. The H.C.F. and L.C.M. of two numbers are 12 and 720. Let’s try to find how many pairs are possible and what may be those numbers.
Solution:
⇒ The factors of 12 are 1,2, 3, 4, 6, and 12.
Case 1 12×1= 12; 720-1 =720
⇒ H.C.F. =12, L.C.M. = 720
∴ (12, 720) is possible.
Case 2 12×2 = 24; 720 + 2 = 360
⇒ H.C.F. = 24, L.C.M. = 360
∴ (24,360) is not possible.
Case 3 12×3 = 36; 720 + 3 = 240
⇒ H.C.F. = 12, L.C.M. = 720,
∴ (36, 240) is possible.
Case 4 12 x 4 = 48; 720 + 4 = 180
∴ (48, 180) is possible.
⇒ H.C.F. = 48, L.C.M. = 720
Case 5 12×6 = 72; 720 + 6=120
⇒ H.C.F. =24, L.C.F. = 360
∴ (72,120) is not possible.
Case 6 12×12= 14; 720 + 2 = 60
⇒ H.C.F. = 12 L.C.M. = 60
∴ (60, 144) is possible.
∴ 4 pairs are (12, 720); (36,240); (48,180), and (60, 144)
Question 21. Let us find the least number from which if 4000 is subtracted, the result will be divisible by 7,11, and 13.
Solution:
⇒ L.C.M. of 7, 11 and 13 = 7×11 x 13 = 1001
∴ Required number = 4000 + 1001 = 5001
Question 22. Let’s find two pairs of numbers between 50 and 100, whose H.C.F. is 16.
Solution:
⇒ 16 x 3 = 48
⇒ 16×4 = 64
⇒ 16×5 = 80
⇒ 16×6 = 96
⇒ 16×7 = 112
⇒ As the numbers are in between 50 and 100.
∴ The numbers are, (64, 80) and (80, 96).
“Easiest method to find HCF and LCM of three numbers Class 6 WBBSE”
Question 23. Let us find a number that is divisible by 28, 33, 42, and 77 and t nearest to 98765.
Solution:
L.C.M. of 28, 33, 42, and 77

L.C.M. = 2 x 3 x 7 x 11 x 2 = 924

∴ The required number = 107 x 924 = 98868.
Question 24. Let us find the least number divisible by 13 such that when the number is divided by 8,12,16 and 20, it leaves 1 as the remainder of all the cases.
Solution:
L.C.M of 8, 12, 16 and 20

⇒ If it leaves 1 as the remainder the number is 240 + 1 = 241 which is not possible as 241 is not divisible by 13.
⇒ Again, the L.C.M is 240 x 2 = 480 and 480 + 1 = 481, it is divisible by 13.
∴ The required number = 481.
