WBBSE Solutions For Class 6 Maths Chapter 14 Concept Of Line Segment Ray And Point

Class 6 Math Solutions WBBSE Chapter 14 Concept Of Line Segment Ray And Point

Let’s draw, observe, and write what I know

My friends and I draw pictures, observe and identify the things we know, let’s note down

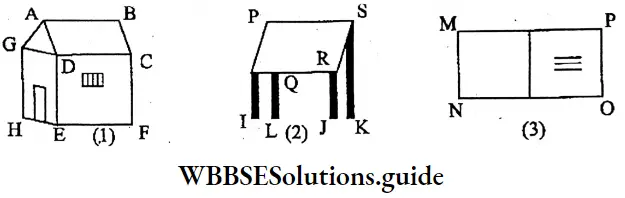
Example 1. Figure (1) is the picture of a ____.
Answer:

⇒ Figure (1) is a picture of a cottage or house.

Example 2. In the picture of the house we can find many ___ [Straight lines or Angular points]
Answer:

⇒ In the picture of the house we can find many Angular points.

“WBBSE Class 6 Maths Chapter 14 concept of line segment ray and point”

Read and Learn More WBBSE Solutions For Class 6 Maths

Example 3. Let’s mention the four angular points — ______, ____, _____, ______ and mark them with ‘O’ in the picture.
Answer:

⇒ The four angular points are A, B, C, and D.

Example 4. Again, we find several ____[Ray/Line segment] in the picture of the house. From Figure (1) let us find and name 4 of the line segments ____, ___, _____, and _____
Answer:

⇒ Again, we find several line segments in the picture of the house. From Figure (1) 4 names of the line segments are AB, BC, CD, and GD.

Example 5. We find the line segments DE and DC are intersecting at ______.
Answer:

⇒ We find the line segments DE and DC intersect at D.

Class 6 Math Solutions WBBSE

Example 6. Again, in Figure (1) ______ and ____ line segments have intersected at E.
Answer:

⇒ Again, in Figure (1) DE and EF line segments have intersected at E

Class 6 History	Class 6 Social Science
Class 6 Geography	Class 6 Science
Class 6 Maths	Class 6 Science MCQs
Class 6 General Science	Class 6 Maths Solutions
Class 6 Geography	Class 6 Hindi

Example 7. But, we see the 2 line segments DE, CF, and the line segments DC and _____ are on the same plane but they will never intersect each other, no matter how far they are produced on either side.
Answer:

⇒ But, we see the 2 line segments DE, CF, and the line segments DC and EF are on the same plane but they will never intersect each other, no matter how far they are produced on either side.

Example 8. The line segments DE and DC are on the same plane and intersect each other at ____, hence these lines are called _____(Intersecting/Parallel).
Answer:

⇒ The line segments DE and DC are on the same plane and are intersecting each other at D, hence these lines are called Intersecting.

Example 9. The line segments DE and CF are on the same plane but will never meet, no matter how far they are produced. Hence, these line segments are (Intersecting/Parallel).
Answer:

The line segments DE and CF are on the same plane but will never meet, no matter how far they are produced. Flence these line segments are parallel.

Class 6 WBBSE Math Solutions Chapter 14 Concept Of Line Segment Ray And Point Exercise 14

Question 1. From the picture (2), let’s identify 4 angular points and name them _______, _________, ________, ______
Solution:

⇒ From the picture (2), let’s identify 4 angular points and name them I, J, K, L.

Question 2. Let’s identify and write the four line segments which are named in the picture (2) _______, ______ and ______
Solution:

Let’s identify and write the four line segments that are named in the picture (2) SP, PQ, QR, and SR.

“WBBSE solutions for Class 6 Maths line segment ray and point”

Question 3. From the picture (2), let’s identify two pairs of intersecting line segments on a plane and find the points at which they intersect.
Solution:

1. SP and PQ are two pairs of intersecting line segments at P as intersecting points.
2. SP and SR are two pairs of intersecting line segments at S as an intersecting point.
3. SR and QR are two pairs of intersecting line segments at R as an intersecting point.
4. QR, and PQ are two pairs of intersecting line segments at Q as an intersecting point.

Question 4. In the picture (2), let’s find two pairs of parallel line segments on a plane that are already named in the figure.
Solution:

⇒ PQ || SR and SP || QR are two pairs of parallel line segments on a plane.

Question 5. From picture (3) — let’s identify and write 3 intersecting points and 4 line segments already named in the picture.
Solution:

3 intersecting points: M, N, O.

4 line segments: MN; NO; OP and PM.

Class 6 Maths Solutions WBBSE Chapter 14 Concept Of Line Segment Ray And Point 14.1

Question 1. Let’s draw 6 concurrent straight lines and name them.
Solution:

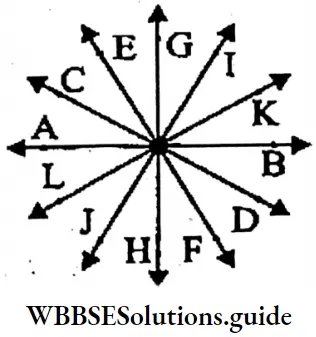
⇒ The 6 concurrent straight lines are \(\overrightarrow{A B}, \overrightarrow{C D}, \overrightarrow{E F}, \overrightarrow{G H}, \overrightarrow{I J}, \ \overrightarrow{K L}\)

“Class 6 Maths WBBSE Chapter 14 line segment ray and point exercises”

Question 2. 5 non-collinear points are to be drawn and find how many straight lines can be drawn through them.
Solution:

A, B, D, and E, are 5 non-collinear points

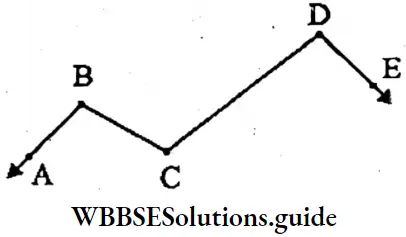
⇒ Through the point A, we can draw 4 straight lines.

⇒ Through the point B, we can draw 3 straight lines.

⇒ Through the point C, we can draw 2 straight lines.

⇒ Through the point D, we can draw 1 straight line

Question 3. Let’s draw 5 points that are collinear.
Solution:

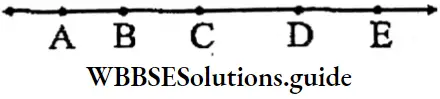
The points A, B, C, D, and E are 5 collinear points.

WBBSE Math Solutions Class 6 Chapter 14 Concept Of Line Segment Ray And Point 14.2

Question 1. Let’s identify the points of intersection in the following figures and note them down.

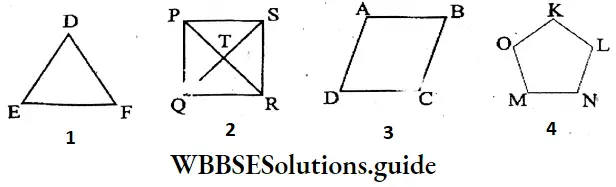
Solution:

1. D, E, and F are the points of intersection.
2. P, Q, R, S, and T are the points of intersection.
3. A, B, C, and D are the points of intersection.
4. K, L, M, N, and O are the points of intersection.

Question 2. In the figures given below, let’s identify line segments and rays and note them down.

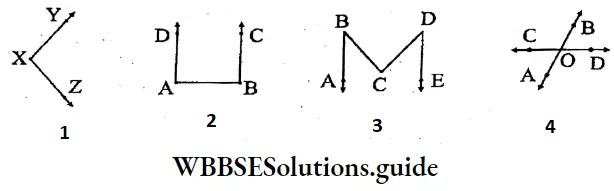
Solution:

1. Line segments = \(\overline{X Y}, \overline{X Z}\)

⇒ Rays = \(\overrightarrow{X Y}, \overrightarrow{X Z}\)

2. Line segments = \(\overline{\mathrm{AD}}, \overline{\mathrm{AB}}, \overline{\mathrm{BC}}\)

⇒ Rays = \(\overrightarrow{A D}, \overrightarrow{B C}\)

“Step-by-step solutions for line segment ray and point Class 6 WBBSE”

3. Line segments = \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DE}}\)

⇒ Rays = \(\overrightarrow{B A}, \overrightarrow{D E}\)

4. Line segments = \(\overline{\mathrm{AB}}, \overline{\mathrm{CD}}\)

⇒ Rays = \(\overrightarrow{O B}, \overrightarrow{O C}\)

Question 3.

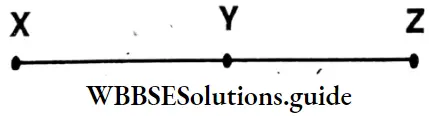
1. What are these three points X, Y, and Z called?
2. How many line segments are formed with these three points?

Solution:

⇒ The points X, Y, and Z are called collinear points.

⇒ Three line segments are formed with these points.

Question 4. From the figure:

1. Let’s find and write three pairs of parallel lines.
2. Let us find and write three pairs of intersecting lines.
3. Let us find and write six-line segments.

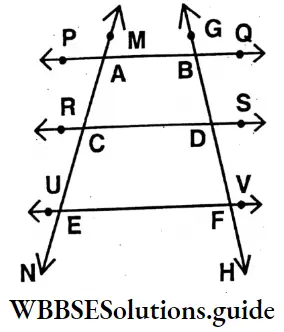
Solution:

1. \((\stackrel{\leftrightarrow}{A B}, \overleftrightarrow{C D}),(\overleftrightarrow{C D}, \overleftrightarrow{E F}),(\stackrel{\leftrightarrow}{A B}, \overleftrightarrow{E F})\)

2. \((\stackrel{\leftrightarrow}{\mathrm{PQ}}, \stackrel{\leftrightarrow}{\mathrm{MN}}) ;(\stackrel{\leftrightarrow}{\mathrm{PQ}}, \overleftrightarrow{\mathrm{G}-1}) \&(\stackrel{\leftrightarrow}{\mathrm{MN}}, \stackrel{\leftrightarrow}{\mathrm{RS}})\)

3. \((\overline{\mathrm{PB}}, \overline{\mathrm{AC}}, \overline{\mathrm{CE}}, \overline{\mathrm{BD}}, \overline{\mathrm{DF}}, \& \overline{\mathrm{AB}})\)

Question 5. From the figure:

1. Let’s find the points of intersection.
2. Let’s write all sets of collinear points separately.
3. Let’s write the line segments separately.
4. Let’s write the concurrent line segments.

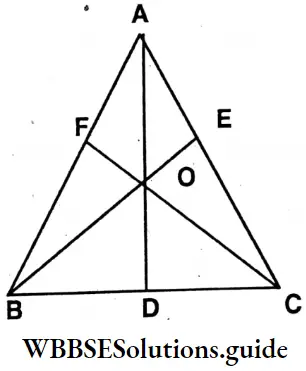
Solution:

1. A, F, B, D, C, E and 0.
2. (A, F, B); (A, O, D), (A, E, C); (B, D, C); (C, 0, F), (B, O, E).
3. AB, BC, CA, AF, FB, AB, AD, OD, BO, BE, OE, CO, CF, OF, AE EC BD DC
4. AD, BE and CF.

Question 6. Let us put (√) for correct and (x) for wrong answers

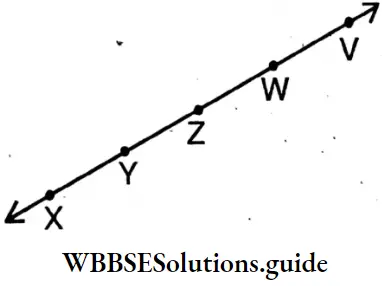
1. On the line segment \(\overrightarrow{\mathrm{YW}}\), Z and W are coliinear.

2. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{WV}}\) are the same rays.

3. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{ZX}}\) are same rays.

4. On the ray \(\overrightarrow{\mathrm{YX}}\), Z is a point.

“WBBSE Class 6 Maths Chapter 14 important questions and answers”

Solution:

1. On the line segment \(\overrightarrow{\mathrm{YW}}\), Y, Z and W are coliinear. (√)

2. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{WC}}\), \(\overrightarrow{\mathrm{WV}}\) WV are the same rays- (√)

3. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{ZX}}\) are the same raYs- (X)

4. On the ray \(\overrightarrow{\mathrm{YX}}\), Z is a point. (X)

Question 7. Let’s try and find the answers

1. How many straight lines can be drawn through one fixed point?
Solution: Infinite

2. How many straight lines can be drawn through two fixed points?
Solution: One

3. How many line segments can be drawn through three non-collinear points?
Solution: Three

4. How many endpoints are there in a line segment \(\overline{\mathrm{AB}}\)?
Solution: A, B

5. How many endpoints are there in ray \(\overrightarrow{\mathrm{AB}}\)?
Solution: A, B

6. Straight line, line segment, and ray — of these three which one has a fixed length?
Solution: Line segment

7. Are the rays \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BA}}\) same?
Solution: Not Same

“Solved examples of line segment ray and point WBBSE Class 6”

8. Are the line segments \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{BA}}\) equal? In what way are they equal?
Solution: Yes

9. What is the maximum number of points at which two line segments can meet?
Solution: One

WBBSE Math Solutions Class 6

10. Let’s find the maximum number of points at which three non-concurrent lines can intersect.
Solution: Three

Question 8. Let’s draw ourselves

1. \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{RS}}\) are two line segments interseceting at O.

2. Using a scale, let us draw \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) and \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) as two Parallel lines

3. Let’s draw a ray \(\overrightarrow{\mathrm{MN}}\) on which S is a point.

4. Let’s draw two line segments AC and DC meeting at C.

Solution:

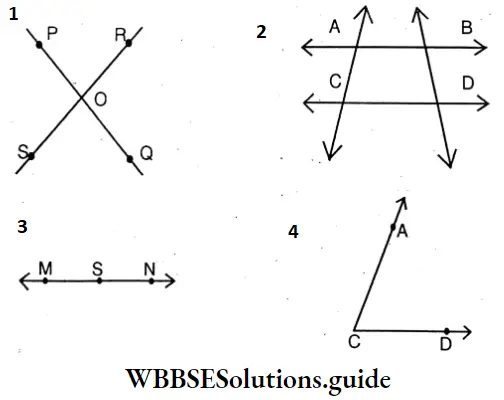
1. PQ and RS are two line segments interesting at O.
2. AB and CD are two parallel line segments.
3. MN is a rayon which S is a point.
4. AC and CD are two line segments meeting at C.

Question 9. From the figure given below, let’s measure the lengths with scale and fill in the blank spaces accordingly.

1. \(\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}\)=____ \(\mathrm{cm} \cdot=\overline{\mathrm{PR}}\)

2. \(\overline{\mathrm{QR}}+\overline{\mathrm{RS}}\) = _____ \(\mathrm{cm}\) = _____

3. \(\overline{\mathrm{PS}}\) = ____ + \(\overline{\mathrm{QR}}\) + _____

4. \(\overline{\mathrm{PR}}-\overline{\mathrm{QR}}\) = _______ cm = _______

5. PR – PQ = ______ cm

6. QS – QR = _______ cm.

7. QS – RS = ______ cm.

Solution:

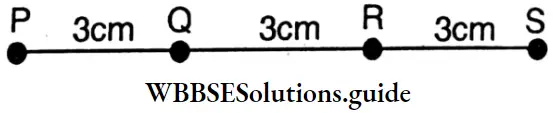
1. \(\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}=(3+3) \mathrm{cm} \cdot=\overline{\mathrm{PR}}=6 \mathrm{~cm}\)

2. \(\overline{\mathrm{QR}}+\overline{\mathrm{RS}}=(3+3) \mathrm{cm} .=\overline{\mathrm{QS}}=6 \mathrm{~cm}\)

3. \(\overline{\mathrm{PS}}=\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}+\overline{\mathrm{RS}}\)

4. \(\overline{\mathrm{PR}}-\overline{\mathrm{QR}}=3 \mathrm{~cm} .=\overline{\mathrm{PQ}}\)

5. \(\mathrm{PR}-\mathrm{PQ}=(6-3) \mathrm{cm}=3 \mathrm{~cm}\)

6. \(\mathrm{QS}-\mathrm{QR}=(6-3) \mathrm{cm}=3 \mathrm{~cm}\)

7. \(\mathrm{QS}-\mathrm{RS}=(6-3) \mathrm{cm}=3 \mathrm{~cm}\)