WBBSE Chapter 18 Square Root Exercise 18
Question 1. 441 oranges were picked from Nisar’s fruit garden. Oranges are to be kept in a basket. Each basket will contain as many oranges as there are many baskets. Let’s calculate to find the number of baskets.
Solution:
⇒ Total number of oranges = 441
⇒ No. of baskets = \(\sqrt{441}=\sqrt{21 \times 21}=21\)
Question 2. Today morning I arranged the books in the almirah of my room. On each shelf, I arranged books equal to the number of shelves of the almirah. But 5 books remained out of the almirah. If the total number of books is 86, let’s find the number of shelves of the almirah.
Solution:
Given
Today morning I arranged the books in the almirah of my room. On each shelf, I arranged books equal to the number of shelves of the almirah. But 5 books remained out of the almirah. If the total number of books are 86,
⇒ Total number of books = 86.
⇒ But 5 books remained out of the almirah.
∴ The total number of books in the almirah = 86 – 5 = 81.
∴ Number of shelves of the almirah = \(\sqrt{81}=\sqrt{9 \times 9}=9\)
Read and Learn More WBBSE Solutions For Class 6 Maths
Question 3. In the playground, we decided to arrange ourselves and stand square. After some have formed this square, it’s found that 4 friends are staying apart. If they join the square, it will not remain square anymore. 40 students are present today in our class. Let’s calculate in this arrangement how many students are there in each row.
Solution:
Given
In the playground, we decided to arrange ourselves and stand square. After some have formed this square, it’s found that 4 friends are staying apart. If they join the square, it will not remain square anymore. 40 students are present today in our class.
⇒ Number of students present today = 40.
⇒ To make a square form 4 students will be excess.
∴ Number of students required to make a square form = 40 – 4 = 36.
∴ Number of students is each row = \(\sqrt{36}=\sqrt{6 \times 6}=6\)
“WBBSE Class 6 Maths Chapter 18 square root solutions”
Question 4. In the Sukanta Memorial Library of our locality, the members contributed as many rupees as there are members. If the total collection is Rs. 729 let’s find the number of members of the library.
Solution:
⇒ Total collections from the members = Rs. 729
⇒ As each members contribute as many rupees as there are members.
∴ Number of members = \(\sqrt{729}=\sqrt{3 \times 3 \times 3 \times 3 \times 3 \times 3}\)
Question 5. To dig a pond in Raghunathpur village, the number of people employed worked for as many numbers of days as there were number of people working, and got as payment Rs. 12375.
Solution:
⇒ Number of people working and get as payment Rs 12375.
⇒ If each, gets daily wage of Rs. 55.
⇒ Number of people joined the work =\(\sqrt{\frac{12375}{55}}=\sqrt{225}=\sqrt{15 \times 15}=15\)
Question 6. If each gets a daily wage of Rs. 55 then let’s find how many pepole joined the work.
Solution:
⇒ The total money collected = Rs. 4096.
⇒ As each member paid an amount 4 times the number of members.
∴ Number of members went for the trip
= \(\frac{\sqrt{4096}}{4}=\sqrt{1024}=\sqrt{4 \times 4 \times 4 \times 4 \times 2 \times 2}\)
= 4x4x2 = 32
Question 7. Today is Children’s Day. Few of us distributed toffee and biscuits among the other students of the school. But 800 toffees were left. So each took twice the number of toffees as we are in number. Let’s calculate among how many of us those 800 toffees were divided.
Solution:
Given
Today is Children’s Day. Few of us distributed toffee and biscuits among the other students of the school. But 800 toffees were left. So each took twice the number of toffees as we are in number.
⇒ Each took twice the number of toffees as we are in number.
⇒ 800 toffee were left.
∴ Number of children = \(\sqrt{\frac{800}{2}}=\sqrt{400}=\sqrt{20 \times 20}=20\)
“WBBSE solutions for Class 6 Maths square root chapter”
| Class 6 History | Class 6 Social Science |
| Class 6 Geography | Class 6 Science |
| Class 6 Maths | Class 6 Science MCQs |
| Class 6 General Science | Class 6 Maths Solutions |
| Class 6 Geography | Class 6 Hindi |
Question 8. Safikul uncle of Atla village brought 780 saplings of papaya tree. He decided to plant them in as many rows as there are number of plants in each row. But by trying to do, he fell short of 4 saplings. In how many rows did Rafikul’s uncle decide to plant the saplings, let’s find.
Solution:
Safikul uncle of Atla village brought 780 saplings of papaya tree. He decided to plant them in as many rows as there are number of plants in each row. But by trying to do, he fell short of 4 saplings.
⇒ The number of saplings of the papaya tree = 780 He fell short of 4 saplings.
∴ Total number of saplings required = 780 + 4 = 784
∴ Number of rows = \(\sqrt{784}=\sqrt{4 \times 4 \times 7 \times 7}\) = 4 x 7 = 28.
Question 9. I made a square cardboard box which has many square cells. Each row has many cells as there are a number of rows. My brother kept one 5 rupee, one two rupee, and a one rupee coin in each cell. If total money kept is Rs. 1152, then let’s find how many cells there are in each row of may cardboard box.
Solution:
Given
I made a square cardboard box which has many square cells. Each row has many cells as there are a number of rows. My brother kept one 5 rupee, one two rupee, and a one rupee coin in each cell. If total money kept is Rs. 1152
⇒ The total money kept is Rs. 1152.
⇒ My brother kept one 5 rupee, a two rupee and a one rupee coin in each cell.
∴ Number of cells = \(\sqrt{\frac{1152}{5+2+1}}=\sqrt{\frac{1152}{8}}\)
= \(\sqrt{144}=\sqrt{12 \times 12}=12\)
“Class 6 Maths WBBSE Chapter 18 square root exercises”
Question 10. Let’s find the value of the following
1. Square of 7 = ____
Solution: Square of 7 = 7 x 7 = 49
2. Square root of 121 = _______
Solution: Square root of 121 = √121
= \(\sqrt{11 \times 11}=11\)
3. 9² = _______
Solution: 92 = 9 x 9 = 81
4. √100 = ______
Solution: \(\sqrt{100}=\sqrt{10 \times 10}=10\)
5. √49 = _________
Solution: \(\sqrt{49}=\sqrt{7 \times 7}=7\)
6. √144 = ______
Solution: \(\sqrt{144}=\sqrt{12 \times 12}=12\)
7. \(\sqrt{3^2 \times 2^2}\) = ________
Solution: \(\sqrt{3^2 \times 2^2}=\sqrt{9 \times 4}\)
= \(\sqrt{36}=\sqrt{6 \times 6}=6\)
8. \(\sqrt{5 \times 7 \times 5 \times 7}\) = ________
Solution: \(\sqrt{5 \times 7 \times 5 \times 7}=\sqrt{5^2 \times 7^2}\) = 5 x 7 = 35
9. \(\sqrt{13 \times 13}\) = _____
Solution: \(\sqrt{13 \times 13}\) = 13
“Step-by-step solutions for square root Class 6 WBBSE”
Question 11. Let’s find the square root of the following by finding factors
1. 169
Solution: \(\sqrt{169}=\sqrt{13 \times 13}=13\)
2. 225
Solution: \(\sqrt{225}=\sqrt{15 \times 15}=15\)
3. 4² + 3²
Solution: \(\sqrt{4^2+3^2}=\sqrt{16+9}\)
= \(\sqrt{25}=\sqrt{5 \times 5}=5\)
4. √144
Solution: \(\sqrt{144}=\sqrt{12 \times 12}=12\)
5. 576
Solution: \(\sqrt{576}=\sqrt{4 \times 4 \times 6 \times 6}\) = 4 x 6 = 24
6. 15² + 20²
Solution: \(\sqrt{15^2+20^2}=\sqrt{225+400}\)
= \(\sqrt{625}=\sqrt{5 \times 5 \times 5 \times 5}\)
= \(5 \times 5=25\)
7. 900
Solution: \(\sqrt{900}=\sqrt{3 \times 3 \times 10 \times 10}\)
Class 6 WBBSE Math Solutions Chapter 18 Square Root Exercise 18.1
Question 1. Let’s find if 108, 64,162, 81 are square numbers or not let us find the smallest whole number other than ‘0’ with which these should be multiplied or divided to give a square number.
1. 108
Solution:

⇒ 108 = 2x2x3x3x3
∴ 108 is not a square number.
⇒ If 3 is multiplied or divided with 108, it will be a square number.
∴ 108 x 3 = 324, a square number or, 108 ÷ 3 = 36, a square number
“WBBSE Class 6 Maths Chapter 18 important questions and answers”
2. √64
Solution:
= \(\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2}\)
=2x2x2=8
∴ 64 is a square number.
3. 162
Solution:

∴162 = 3x3x3x3x2
∴ 162 is not a square number.
⇒ If 2 is multiplied or divided with 162, it will be a square number.
∴ 162 x 2 = 324 = 18 x 18, a square number,
or, 162 ÷ 2 = 81 = 9 x 9, a square number.
4. √81
Solution:
= \(\sqrt{3 \times 3 \times 3 \times 3}\) =3×3 = 9
∴ 81 is a square number.

Class 6 Maths Solutions WBBSE Chapter 18 Square Root Exercise 18.2
Question 1. Apart from 0, by which least whole number the following numbers must be divided to get square numbers
- 845
- 450
- 18 x 6
- 25 x 35
1. 845
Solution:

845 = 13x13x5
⇒ Hence, it is not a square number.
⇒ If we divide the number by 5, we will get a square number.
∴ The required number is 5.
2. 450
Solution:

∴ 450 = 5x5x3x3x2
⇒ Hence, it is not a square number, if we divide the number by 2, it will be a square number.
∴ The required number is 2.
“Solved examples of square root WBBSE Class 6”
3. 18×6
Solution:
= (3 x 3 x 2) x (2 x 3)
=3x3x2x2x3
⇒ Hence, it is not a square number, if we divide the number by 3, it will be a square number.
∴ The required number is 3.
4. 25 x 35 = (5 x 5) x (5 x 7)
Solution:
⇒ Hence, it is not a square number, if we divide the number by 35 (5 x 7), it will be a square number.
∴ The required number = 35.
Question 2. By which least whole number apart from 0, the following numbers should be multiplied to give a square number:
1. 432
Solution:

=2x2x3x7x7x3
⇒ Hence, 588 is not a square number, if we multiply 3 with it, it will be a square number.
∴ The required number is 3.
Class 6 Maths Solutions WBBSE
2. 588
Solution:

= 2x2x3x7x7x3
⇒ Hence 588 is not a square number, if we multiply 3 with it, it will be a square number.
∴ The required number is 3
3. 25×20
Solution:
= 5x5x2x2x5
⇒ Hence, it is not a square number, if we multiply 5 with it, it will be a square number.
∴ The required number is 5.
4. 24x 28
Solution:
=2x2x2x3x2x2x7
⇒ Hence, it is not a square number, if we multiply 2x3x7 with it, it will be a square number.
∴ The required number is 2 x 3 x 7 = 42.
WBBSE Math Solutions Class 6 Chapter 18 Square Root Exercise 18.3
Question 1. Let’s work out to find the least square number other than 0, which is divisible by 12,16, 20, and 24.
Solution:

∴ L.C.M.of 12, 16, 20 and 24 = 2x2x2x2x3x5 = 240
⇒ Hence, 240 is not a least square number
⇒ If we multiplied 240 by 3 x 5, then it will be the least square number.
∴ The required least square number.
= 240 x 3 x 5 = 3600.
Question 2. The product of two positive whole numbers is 98 and the greater one is twice the smaller number. Let’s find the two numbers.
Solution:
⇒ Greater number = 2x smaller number
⇒ Greater number x smaller number = 98
⇒ or, (2 x smaller number) x smaller number = 98
⇒ or, 2 x (smaller number)² = 98
∴ (Smaller number)² = 98/2 = 49
∴ Smaller number = √49 =7
∴ Greater number = 2 x smaller number = 2×7 = 14
∴ The required numbers are 7 and 14.
Question 3. Let’s find which least square number has factor 17.
Solution: The least square number which has a factor =17×17 = 289
Question 4. Let’s find the least square number other than 0 which is divisible by 10,15,20 and 30. Also, let’s write the next square number which will be divisible by these numbers.
Solution:

∴ L.C.M. = 2x2x3x5 = 60
⇒ It is not a square number. If we multiplily by 3 x 5, we will get a square number.
∴ Least square number = 60 x 3 x5 = 900.
∴ The next square number = 900 x 4 = 3600.
WBBSE Math Solutions Class 6
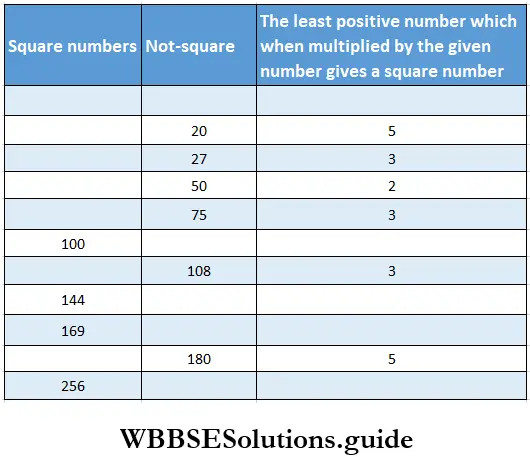
Question 5. Let’s analyse the given numbers and place them in their respective columns-20, 27, 50, 75, 100, 108,144, 169,180, 256
Solution:
⇒ 20 = 2 x 2 x 5 – it is not a square number
⇒ 27 = 3 x 3 x 3 – it is not a square number
⇒ 50 = 5 x 5 x 2 – it is not a square number
⇒ 75 = 5 x 5 x 3 – it is not a square number
⇒ 100 = 2 x 2 x 5 x 5 – it is a square number
⇒ 108 = 6 x6 x 3 – it is not a square number
⇒ 144 = 2 x 2 x 6 x 6 – it is a square number
⇒ 169 = 13 x 13 – it is a square number
⇒ 180 = 2 x 2 x 3 x 3 x 5 – it is not a square number
256 = 4 x 4 x 4 x 4 – it is a square number
Question 6. This year on Netaji’s birthday, the students present in Physical Education class were made to stand in rows of 18,24,27, at different points of time, to march past At one point of time we formed a solid square. Let us find the least number of students present in school on that day.
Solution: L.C.M of 18, 24, 27

= 2 x 2 x 2 x 3 x 3 x 3
= 216
⇒ It is not a square number, if we multiply 2×3 with it, it will be a square number.
∴ Least number of students = 216x2x3 = 1296
WBBSE Math Solutions Class 6
Question 7. The product of two positive numbers is 147. The greater number is 3 times the smaller number. Let’s find the numbers.
Solution:
⇒ Greater number = 3 x smaller number .
⇒ Greater number x smaller number = 147
⇒ or, 3 x smaller number x smaller number = 147
⇒ or, (Smaller number)² = 147/3 = 49
∴ Smaller number = √49 = 7
⇒ Greater number = 3×7 = 21.
“Best guide for Class 6 Maths WBBSE square root problems”
Question 8. Arrange the following in ascending order of their value:
⇒ \((\sqrt{36}+\sqrt{25}),(\sqrt{49}+\sqrt{9}) ;(\sqrt{25}+\sqrt{100}),(\sqrt{4}+\sqrt{16})\)
Solution:
⇒ \((\sqrt{36}+\sqrt{25})\)
= 6 + 5 = 11
⇒ \((\sqrt{49}+\sqrt{9})\)
= 7 + 3 = 10
⇒ \((\sqrt{25}+\sqrt{100})\)
= 5 + 10 = 125
⇒ \(\sqrt{4}+\sqrt{16}\)
= 2 + 4 = 6
⇒ In ascending order
6 ∠ 10 ∠ 11 ∠ 15
i.e., \(\sqrt{4}+\sqrt{16} ; \sqrt{49}+\sqrt{9} ; \sqrt{36}+\sqrt{25} ; \sqrt{25}+\sqrt{100}\)
WBBSE Class 6 Maths Solutions
Question 9. Of three positive numbers, the product of first and second is 24 second and third is 48 and that of first and third is 32. Let’s find the three numbers.
Solution:
⇒ 1st number x 2nd number = 24
⇒ 2nd number x 3rd number = 48
⇒ 1st number x 3rd number = 32
⇒ (1st number x 2nd number) x (1st number x 3rd number)/ (2nd number x 3rd number)
∴ (1st number)² = 16
∴ 1st number = √16 = 4
⇒ Again, 1st number x 2nd number = 24
⇒ or, 4 x 2nd number = 24
∴ 2nd number = 24/4 = 6
⇒ Again, 2nd number x 3rd number = 48
⇒ 6 x 3rd number = 48
∴ 3rd number = 48/6 = 8
∴ Required numbers are 4, 6, and 8.
Question 10. On Republic Day, our Physical Education teacher made all students stand in rows having 12,15, and 20 students, at different points of time, for march past. At one point of time, the students were arranged in solid square. Let’s find out at least how many students were present in school on that day.
Solution:
L.C.M. of 12, 15 and 20

= 2 x 2 x 3 x 5
⇒ But 60 is not a square number, if we multiply 3 and 5 with it, it will be square number.
∴ The required number = 60 x 3 x 5 = 900.
WBBSE Class 6 Maths Solutions Chapter 18 Square Root Exercise 18.4
Question 1. Let’s find the square number nearest to 1000.
Solution:
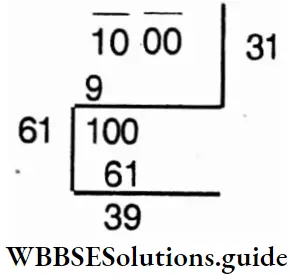
∴ 1000 – 39 = 961 is a square number.
∴ √961 = 31
⇒ Next square number is (32)² = 1024
⇒ 1024- 1000 = 24 ∠ 39
∴ Square number nearest to 1 000 is 1024.
Question 2. Let’s find the least number that will be subtracted from 9585 to give a square number.
Solution:
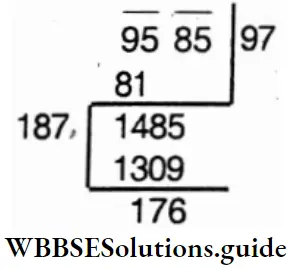
∴ The required number is 176.
Question 3. Let’s find what least number must be added to 5320 to make it a perfect square.
Solution:
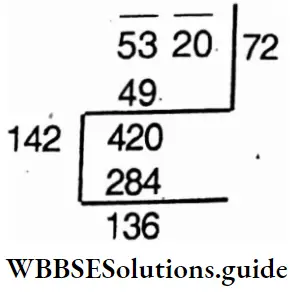
Next square number is (73)² = 5329.
∴ The required number that is to be added to 5320 to make a square number is 5329-5320 = 9.
Question 4. Let’s find the least square number other than 0, which is divisible by 15, 25, 35, 45.
Solution:
L.C.M.of 15,25, 35 and 45
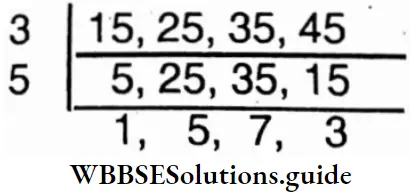
= 3x5x5x7x3 = 1575.
⇒ It is not a square number, if we multiply 7 with it, it will be a square number.
∴ The required least square number = 1575 x 7 = 11025.
Question 5. Let’s find the least square number of 4 digits which are divisible by 8, 15, 20, and 25.
Solution:
L.C.M. of 8, 15, 20 and 25

= 2 x 2 x 5 x 2 x 3 x 5 = 600
⇒ If we multiply 600 by 2 and 3 then we get a square number.
∴ The least-square number of 4 digits = 600 x 6 = 3600.
Question 6. Let’s find the least square number of 4 digits.
Solution:
The least 4 digit number is 1000.

⇒ 1000- 39 = 961 is a square number.
⇒ √961 =31
⇒ Next square number = (32)² = 1 024.
∴ Least square number of 4 digits = 1 024.
“How to calculate square root easily Class 6 WBBSE”
Question 7. Let’s find the greatest square number of 4 digits.
Solution:
⇒ The greatest number of 4 digits = 9999.
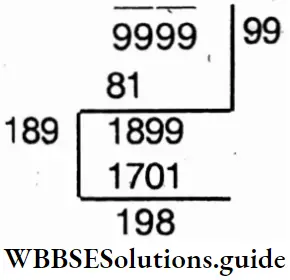
⇒ The greatest square number of 4 digits = 9999 -198 = 9801.
Question 8. Let us find the square root of the following by the method of division:
Solution:
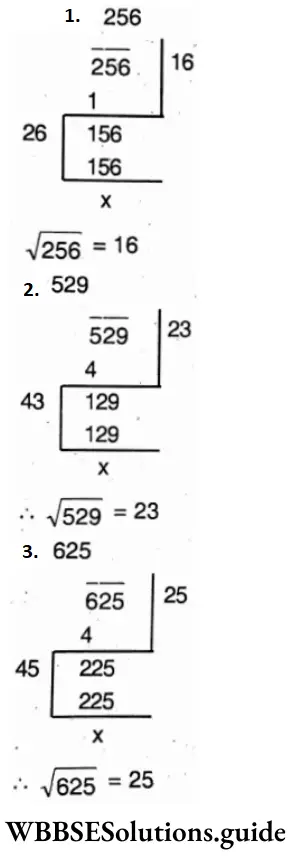
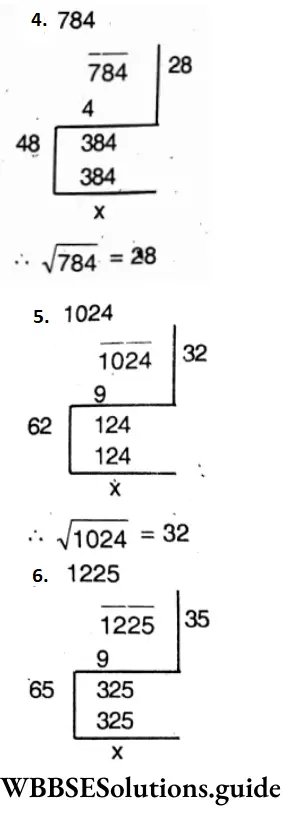
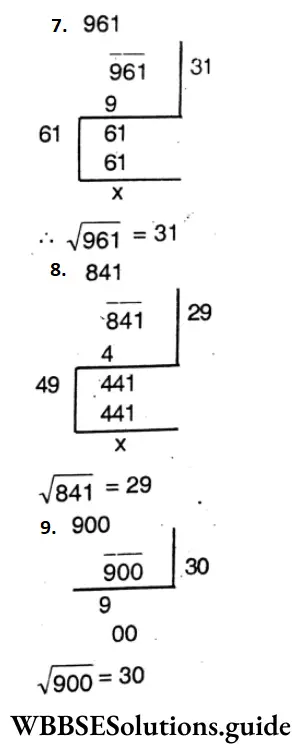

Question 9. Without finding square root, let us find the possible digits in unit’s place and number of digits in the square root number:
1. 784
Solution:
⇒ Possible digits in unit’s place = 2, 4
∴ Number of digits in the square root number = 2
Class 6 Math WBBSE Solutions
2. 3676
Solution:
⇒ Possible digits in 4 unit’s place = 6
∴ Number of digits in the square root number = 2
3. 160000
Solution:
⇒ Possible digits in unit’s place = 0
⇒ Number of digits in the square root number = 3
4. 1225
Solution:
Possible digits in unit’s place = 5
∴ Number of digits in the square root number = 2
5. 2401
Solution:
⇒ Possible digits in unit’s place = 1,9
∴ Number of digits in the square root number = 2
6. 10201
Solution:
⇒ Possible digits in unit’s place =,1,9.
∴ Number of digits in the square root number = 3
“Understanding square root concepts for Class 6 WBBSE Maths”
Question 10. Let’s find two square numbers nearest to 5000.
Solution: 5000

⇒ Nearest to 5000 = (70)² and (71)²
= 4900 and 5041
Question 11. The product of two numbers is 1576 and their quotient is 9/7, let’s find the numbers.
Solution:
⇒ 1st number x 2nd number = 1575
and \(\frac{1 \text { st number }}{2 \text { nd number }}=\frac{9}{7}\)
∴ \((1 \text { st number } \times 2 \text { nd number }) \times \frac{1st number }{2nd num ber}=1575 \times \frac{9}{7}\)
∴ (1st number)² = 225 x
⇒ 1st number = \(\sqrt{225 \times 9}\) = 15 x 3 = 45
∴ 2nd number = 1575 ÷ 45 = 35
∴ The numbers are 45, 35.
Question 12. Let us find what digit will be placed in * of 202*, so that it becomes a square number.
Solution: 202 *
⇒ 1 st if we put 1, then 2021 is not a square number.
⇒ 2nd if we put 2, then 2022 is not a square number.
⇒ 3rd if we put 3, then 2023 is not a square number.
⇒ 4th, if we put 4, then 2024 is not a square number.
⇒ 5th if we put 5, then 2025 is a square number.
∴ The required digit is 5.
