Class 6 WBBSE Math Solutions Chapter 22 Drawing Of Different Geometrical Figures Exercise 22
Question 1. In the following figures, let’s identify which two straight lines have intersected at right angles.
Solution:
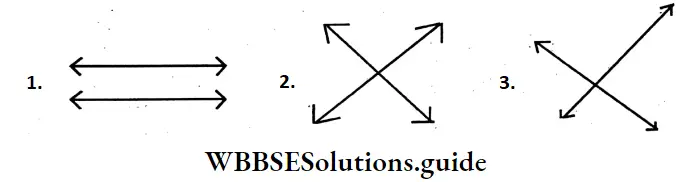
In the figures (2) and (3), the two straight lines intersected at right angles.
Question 2. Let’s fill in the blanks:
1. At 3’o clock the arms of the clock will be at _____
Solution: A 3’o clock the arms of the clock will be at [right angles].
2. The straight lamp post on the road is at _______ to the ground.
Solution: The straight lamp post on the road is at [right angles] to the ground.
Question 3. Let me write two such things which are at right angles to each other.
Solution: Walls and the floor of a room are at right angles to each other.
Read and Learn More WBBSE Solutions For Class 6 Maths
Question 4. Let us draw a line segment AB of length 4 cm; a point O is taken on the line segment AB, such that AO = 1 cm and OB = 3 cm. Now, at O, let’s draw a perpendicular AB.
Solution:
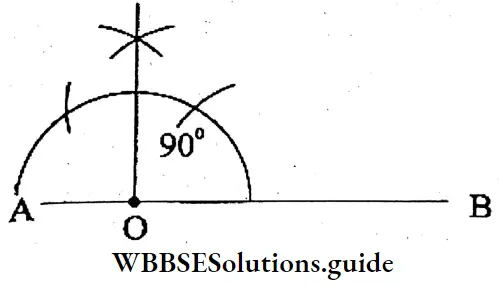
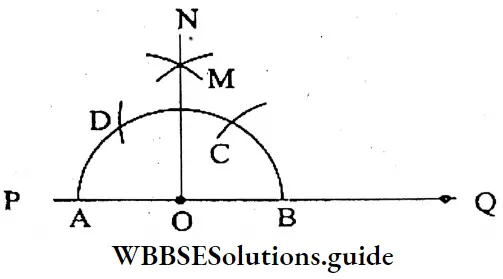
Question 5. A line segment PQ of length 4 cm is drawn. A point O is taken on the segment PQ. With the help of scale and pencil, compass, let’s draw perpendicular OM on PQ at O.
“WBBSE Class 6 Maths Chapter 22 drawing of different geometrical figures solutions”
Solution:
| Class 6 History | Class 6 Social Science |
| Class 6 Geography | Class 6 Science |
| Class 6 Maths | Class 6 Science MCQs |
| Class 6 General Science | Class 6 Maths Solutions |
| Class 6 Geography | Class 6 Hindi |
Draw a line segment PQ of 4 cm. Take a point O on PQ. Now, a perpendicular OR is drawn on PQ at O.

Question 6. A line segment XY of length 5 cm is drawn. A point P is taken outside the line segment XY. With a set square, let’s draw a perpendicular PL, on line segment XY from point P.
Solution:
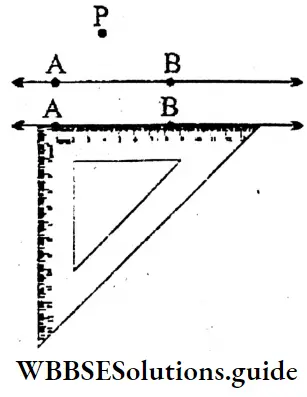
⇒ A line segment XY of length 5 cm is drawn. A point is taken outside the line segment XY.
⇒ Now, with the help of a scale and a set square, I draw a perpendicular PL on the line segment XY from the point P.
“WBBSE solutions for Class 6 Maths geometrical figures drawing”
Question 7. A line segment AB of length 8 cm is taken. A point P is taken on the line segment AB, so that AP = 3 cm, and BP = 5 cm, let’s draw a perpendicular PL on the line segment AB, at point P with the help of scale and pencil and a compass.
Solution:
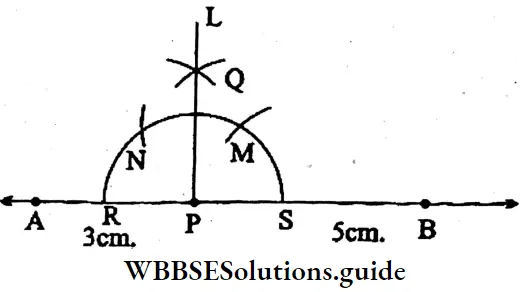
⇒ Draw a straight line AB of 8 cm. A point P is taken on AB, such that AP – 3 cm and PB = 5 cm.
⇒ Now, a perpendicular PL is drawn on AB at P with a scale pencil and a compass.
Question 8. A line segment AB of length 6 cm is drawn. Let’s take a point K outside this line segment. With the help of scale and compass, let’s draw a perpendicular KL on the line segment AB.
Solution:
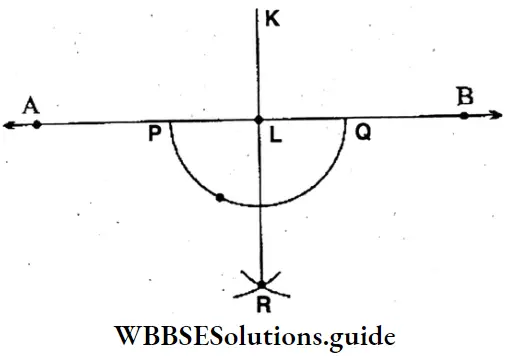
⇒ A straight line AB of length 6 cm is taken. A point K is taken outside AB. Now, with centre K, an arc is drawn which cuts AB at P and Q.
⇒ Now, with centre P and Q, two arcs with radii more than 1/2 of PQ are drawn, which cut each other at R. Join KR which cuts AB at L. KL is the required perpendicular on AB.
“Class 6 Maths WBBSE Chapter 22 drawing geometric shapes exercises”
Question 9. Let’s draw a triangle ABC with the help of scale and pencil. From the three vertices A, B and C of the triangle, perpendiculars AP, BQ and CR are drawn on the sides BC, AC and AB respectively. Let’s see from the figure, if the line segments AP, BQ and CR are concurrent, i.e., they intersect at a point.
Solution:
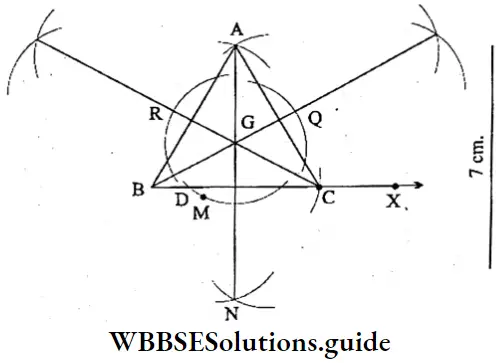
⇒ A triangle ABC is drawn. From three vertices A, B and C of the triangle ABC, three perpendiculars AP, BQ and CR are drawn. The three perpendiculars AP, BQ and CR meet at O, i.e., perpendiculars are concurrent.
“Step-by-step solutions for drawing geometrical figures Class 6 WBBSE”
Question 10. With the help of a set square, let us draw a right-angled triangle ABC such that ABC = ∠90°. From point B, let’s draw a perpendicular on the hypotenuse AC. Let’s also find if the perpendiculars from A, B and C on the opposite sides meet at point. If so, name the point.
Solution:
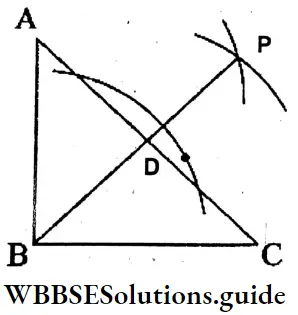
⇒ ABC is a right-angled triangle, ABC = ∠90°. A perpendicular BD is drawn on AC. AB is perpendicular on BC from point A and BC is particular on AB from point C.
⇒ These three perpendiculars meet at B.
Question 11. At a fixed point on a straight line ___ perpendicular can be drawn.
Solution: At a fixed point on a straight line one perpendicular can be drawn.
Question 12. From a fixed point outside a straight line _____ (one/more than one) perpendicular can be drawn to that straight line.
Solution: From a fixed point outside a straight line one perpendicular can be drawn to the straight line.
“WBBSE Class 6 Maths Chapter 22 important questions and answers”
Question 13. Let’s draw a line segment AB, let’s take any two points P and Q on the line segment. Let’s draw two perpendiculars PM and QN at P and Q on the line segment AB; let’s find if line segments PM and QN are parallel or intersecting.
Solution:
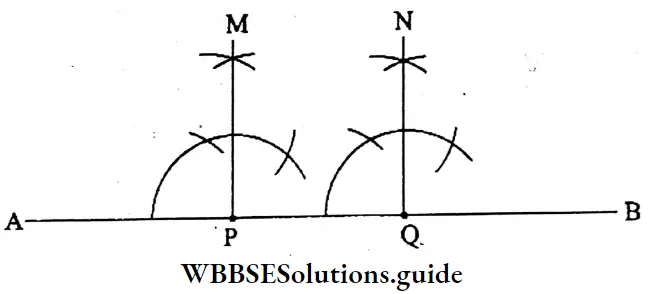
Let P and Q are the two points on the line segment AB. Two perpendiculars r PM and QN are drawn on AB at P and Q. Here PM and QN are two parallel lines.
Question 14. Let’s draw a line segment of length 4 cm; taking this length as radius a circle is drawn. Let the centre of the circle be named O. A chord AB which is not a diameter is drawn. From O a perpendicular OM is drawn on the chord AB. Let’s measure the line segments AM and BM with a scale and write the conclusion derived.
Solution:
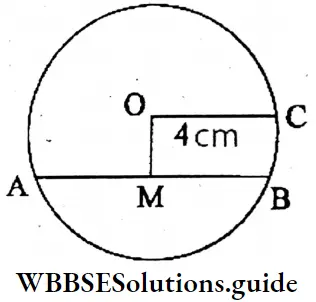
⇒ O is the centre of the circle of radius 4 cm (OC).
⇒ AB is a chord. A perpendicular OM is drawn from the centre O. AB is bisected at M.
⇒ AB = 6.6 cm; AM = BM = 3.3 cm.
Class 6 Maths Solutions WBBSE Chapter 22 Drawing Of Different Geometrical Figures Exercise 22.1
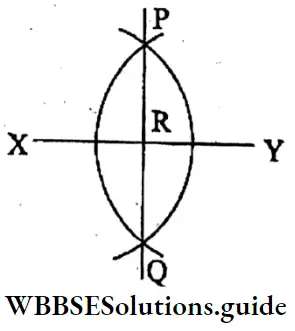
I drew a line segment XY with scale and pencil on my exercise book. I Now we shall draw the perpendicular bisector of line segment XY with the help of scale, pencil and pencil compass.
Solution:
⇒ A line segment XY is drawn with a scale and pencil. Now, with centres X and Y, two arcs with the same radius are drawn on both sides of XY.
⇒ The arcs intersect each other at C and D. Join C and, D which cuts XY at P.
∴ XP = PY = 4 cm.
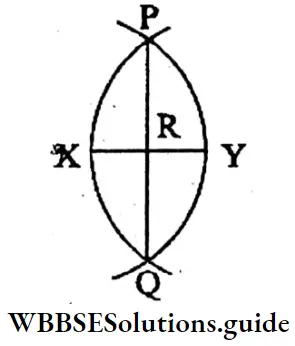
Question 1. If take a radius, less than half the length of the line segment XY and try to draw an arc with centres X and Y, on both sides, what shall I find?
Solution: Now, with centres X and Y, we draw two arcs with a radius less than half the length of line segment XY on both sides.
Question 2. Again, if I draw arcs with centres X and Y and a radius equal to the length 1 more than half the length of the line segment, what shall I observe?
Solution:
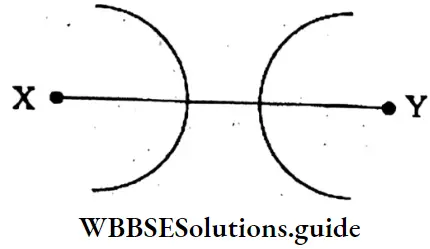
⇒ Again, with centres X and Y, we draw two more arcs with a radius half of the length of line segment XY.
⇒ The two arcs cut the previous arcs at QR and MN.
WBBSE Math Solutions Class 6 Chapter 22 Drawing Of Different Geometrical Figures Exercise 22.2
Question 1. Let’s draw a line segment AB of length 5 cm with scale and pencil. By folding the paper, let us find the perpendicular bisector of the line segment AB. Then, we actually measure the two bisected parts with scale.
Solution:
1. Let’s take a thick paper. It is folded at any end and then unfolded. The line formed by the fold is marked with a pencil.
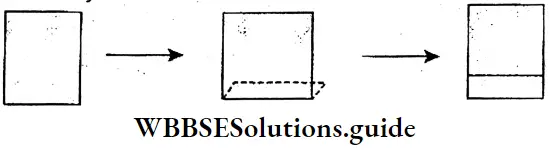
2. On this, two points A and B are taken. Now the paper is again folded in such a way that points A and B coincide. Again, on this fold mark a line segment. CD is drawn and we get the mid point of the line segment AB. That D is the midpoint of the line segment AB and the line segment CD is perpendicular at D on line segment AB.
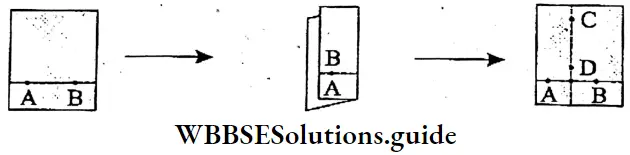
Hence, the line segment CD is perpendicular to the line segment AB at its midpoint. Line segment CD is called the Perpendicular Bisector of the line segment AB.
The perpendicular bisector of a line segment divides it into two equal parts.
“Solved examples of geometrical figure drawing WBBSE Class 6”
Question 2. Let’s draw a line segment of length 8 cm with scale and pencil. Then let’s draw a perpendicular bisector of this line segment and each part measured.
Solution:
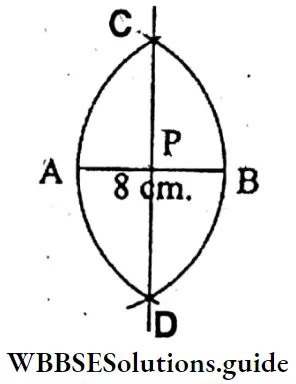
Let AB is a line segment of 8 cm. Now with centres A and B two arcs with radii more than 1/2 of AB are drawn on both sides of AB. They intersect each other at C and D. Join C, D which cuts AB at P.
AP = PB = 4 cm.
Question 3. Let’s draw a line segment PQ of length 6 cm with scale and pencil, now, taking line segment PQ as diameter, let’s draw a circle.
Solution:
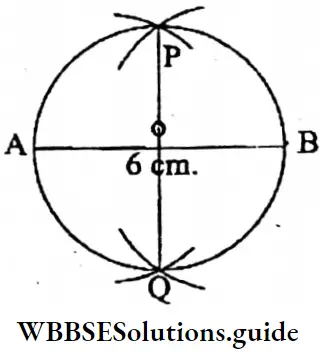
Let PQ is a line segment of length 6 cm. It is bisected at O. Now, with centre O and radius PO a circle is drawn.
“Best guide for Class 6 Maths WBBSE drawing geometrical figures”
Question 4. With the help of scale and pencil, a line segment AB of length 8 cm is drawn. Let’s divide the line segment AB into four equal parts and measure each part.
Solution:
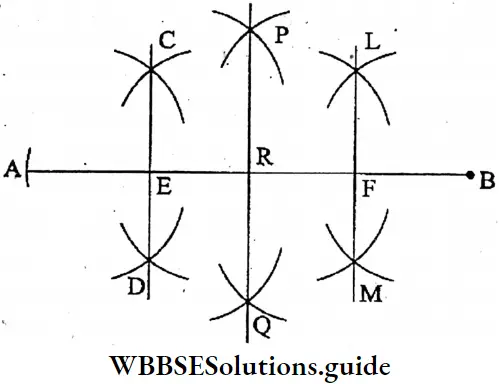
- First we bisect the line segment AB into equal parts such that AR = RB.
- Again, we bisect the line segment AR and RB into two equal parts such that AE = ER and RF = FB. Hence, the segment AB is divided four equal parts.
∴ AE = EF = RF = FB = 2 cm.
WBBSE Math Solutions Class 6
Question 5. Let’s draw two circles whose diameters are 5 cm and 7 cm respectively.
Solution:
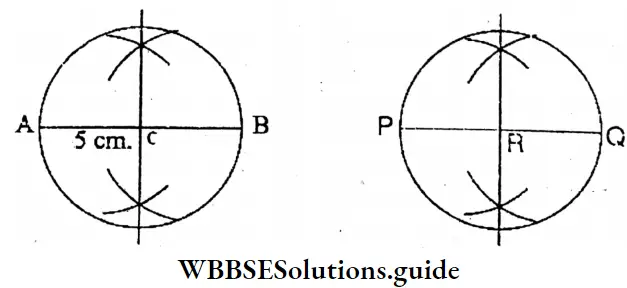
⇒ AB and PQ are two line segments of lengths 5 cm and 7 cm respectively. Line segment AB is bisected at C and line segment PQ is bisected at R.
⇒ Now, with centres C and R two circles are drawn with radii of 2.5 cm and 3.5 cm respectively.
Question 6. Masum drew a triangle ABC. Then with the help of scale and pencil, compass, she bisected the sides BC, AC and AB perpendicularly. She verified that the three perpendicular bisectors are concurrent. When found concurrent, she named it O. Now with centre O and radius equal to the line segment AO, she drew a circle.
Solution:
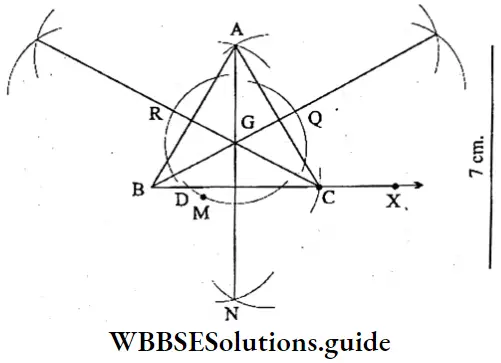
ABC is a triangle, the sides BC, CD and DA are bisected at D, E, and F. These 3 bisectors meet at O. Now, with centre O and radius OA, a circle is drawn which passes through B and C. Point O is called circumcentre of the triangle ABC.
WBBSE Class 6 Maths Solutions Chapter 22 Drawing Of Different Geometrical Figures Exercise 22.3
Question 1. Let us draw the following angles with the help of protractor: 30°, 42°, 105°, 67°, 88°, 120°, 205°, 282°.
Solution:
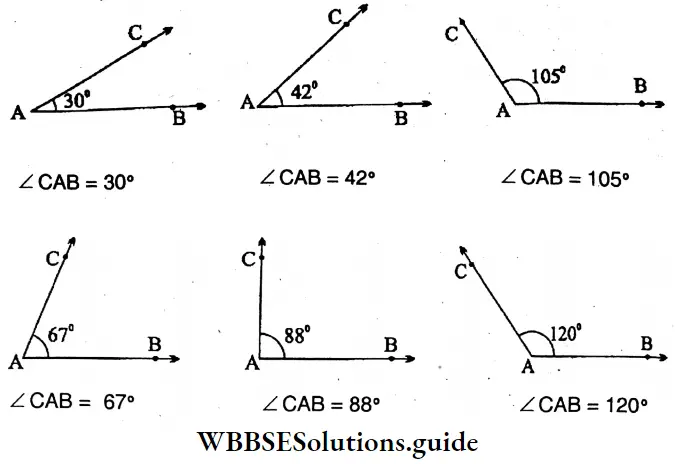
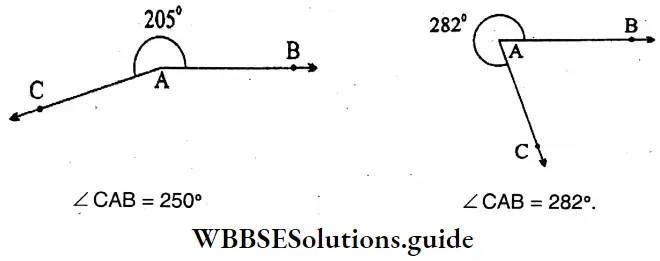
Question 2. When a clock shows the following time, the angles formed by their arms are to be drawn with a protractor on the exercise book.
1. 3 p.m.
Solution: At 3 p.m.: The angle formed by the arms is 90°.
2. 5 a.m.
Solution: At 5 p.m.: The angle formed by the arms is 150°.
3. 10a.m
Solution: At 10 a.m.: The angle formed by the arms is 60°.
4. 4 p.m.
Solution: At 4 p.m.: The angle formed by the arms is 120°.
WBBSE Class 6 Maths Solutions
Question 3. Let’s draw the following angles with the help of set square and bisect them with a scale, pencil and compass.
1. 30°
Solution:
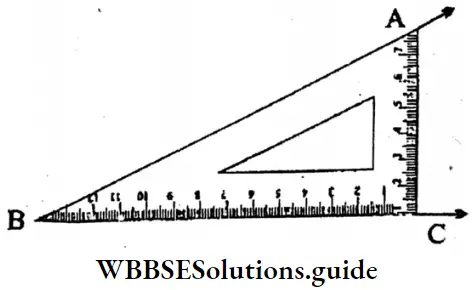
⇒ ∠ABC = 30°
⇒ PB is the bisector ∠ABC.
2. 45°
Solution:
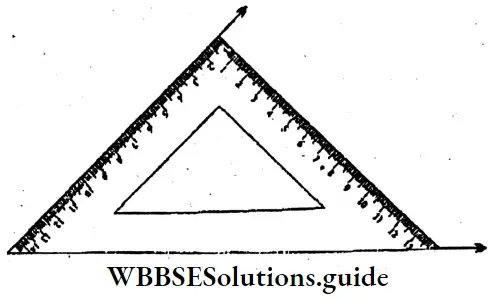
⇒ ∠PQR = 45°
⇒ QC is the bisector ∠PQR.
3. 60°
Solution:
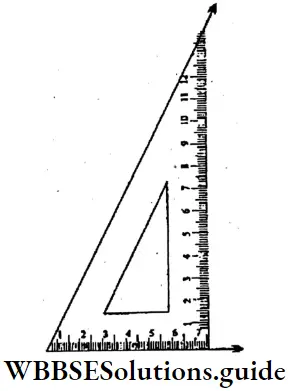
⇒ ∠MBN = 60
⇒ BR is the bisector of ∠MBN.
4. 90°
Solution:
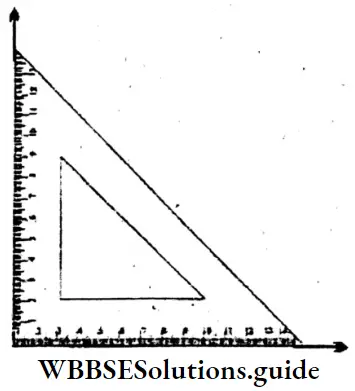
∠XYZ = 90°
YP is the bisector of ∠XYZ.
5. 105°
Solution:
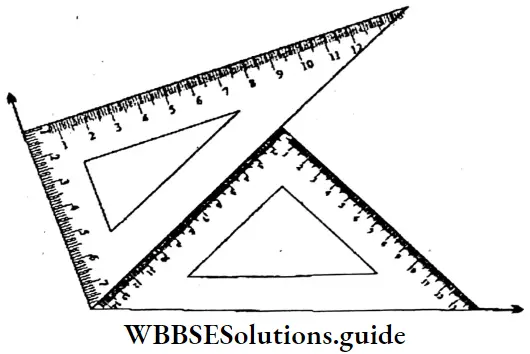
⇒ ∠ABC = V ABR + VRBC = 60° + 45° = 105°
⇒ ∠BK is the bisector of ∠ABC.
“How to draw geometric shapes using instruments Class 6 WBBSE”
Question 4. Without using a protractor let us draw an angle of 45° with a scale, pencil, compass.
Solution:
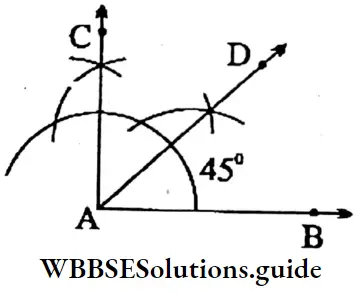
⇒ 1st BAC = 90° is drawn
⇒ Now, ∠BAC is bisected, ∠BAD = 45°, and ∠CAD = 45°.
Question 5. Let’s draw an angle of 120° with the help of a protractor, then divide it into 4 equal parts with the help of scale, pencil and compass.
Solution:
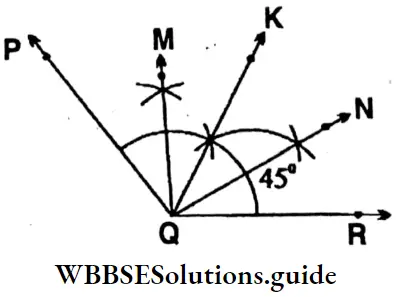
⇒ With the protractor 1st ∠PQR = 120° is drawn. Now, 1st bisect the ∠PQR into two equal parts.
⇒ QK is the bisector of ∠PQR. The two equal angles are ∠PQK and ∠KQR, each equal to 60°.
⇒ Again, bisect two angles ∠PQK and ∠KQR.
∴ 4 equal parts of ∠PQR are ∠PQM = ∠MQK = ∠KQN = ∠NQR = 30°.
“Understanding geometry drawing concepts for Class 6 WBBSE Maths”
Question 6. Let’s draw a triangle ABC with the help of a scale and pencil. Then the three angles of the triangle are bisected. Let’s find if the bisectors of the angles are concurrent.
Solution:
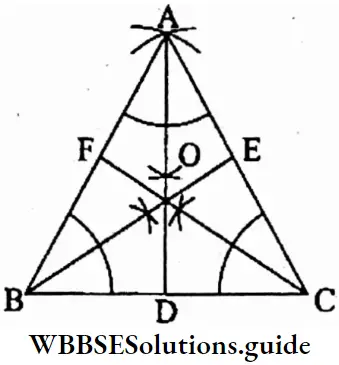
Let ABC is a triangle. Its 3 angles are ∠BAC, ∠ABC and ∠ACB. Now, with the help of a compass and scale these angles are bisected.
AD, BE and CF are the three bisectors of the angles respectively. The bisectors of the angles meet at O. The point ‘O’ is called the in centre of the triangle.
Question 7. Let’s draw any angle ∠PQR using a scale, pencil and compass. Z PQR is bisected and the bisector of ∠RQP is produced up to point X. Again with scale, pencil and compass, ∠PQS is bisected by QY. What angle do QX and QY line segments make with each other? — Let us measure by protractor.
Solution:
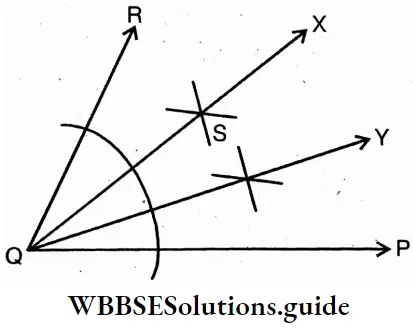
⇒ Angle PQR is drawn using scale. Now, with help of compass ∠PQR is bisected. ∠PQR = 70°
⇒ QS is the bisector of ∠PQR.
∴ ∠RQS = ∠SQP = 35°.
⇒ Again, ∠PQS is bisected by QY with a compass.
∴ ∠SQY= ∠YQP = 17.5°.
∴ ∠XQY= ∠YQP = 17.5°.
“WBBSE Class 6 Maths geometrical drawing step-by-step guide”
Question 8. Let’s draw a line segment PQ. At points P and Q of PQ, two perpendiculars PR and QS are drawn with scale, pencil and compass, ∠QPR and ∠PQS are bisected using scale, pencil and compass. The triangle so formed — its angles are measured and their values are written.
Solution:
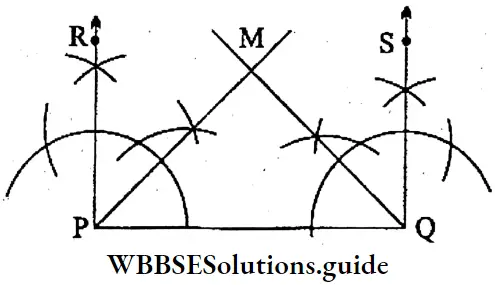
⇒ PQ is a line segment. At P and Q two perpendiculars RP and SQ are drawn with the help of scale and compass.
∴ ∠RPQ = ∠SQP = 90°.
⇒ Again, ∠RPQ and ∠SQP are bisected with the help of scale and compass. The bisectors meet each other at A. Therefore, ΔAPQ is formed.
⇒ Now, ∠APQ = 1/2 of 90° = 45°
and ∠AQP = 1/2 of 90° = 45°
∴ ∠PAQ = 180°- (45° + 45) = 180°- 90° = 90°.
