Class 6 WBBSE Math Solutions Chapter 25 Fun With Numbers Exercise 25
Question 1. Let’s observe the interesting numbers.
Solution:
Let’s observe the interesting numbers
⇒ 11 x 11 = 121
⇒ 11 x 11 x 11 = 1331
⇒ 11 x 11 x 11 x11 = 14641
⇒ 11 x 11 x 11 x 11 x 11 = 161051
Other interesting numbers
⇒ 10 x 1 = 10; 1+0=1
⇒ 11 x 1 = 11; 1+1=2
⇒ 12 x 1 = 12; 1+2=3
⇒ 13 x 1 = 13; 1+3=4
⇒ 14 x 1 = 14; 1+4=5
⇒ 15 x 1 = 15; 1+5=6
⇒ 16 x 1 = 16; 1+6=7
⇒ 17 x 1 = 17; 1+7=8
⇒ 18 x 1 = 18; 1+8=9
⇒ 19 x 1 = 19; 1+9=10
Read and Learn More WBBSE Solutions For Class 6 Maths
An interesting arrangement of the square and square root of natural number.
⇒ 1 =1 =1²
⇒ 1 + 3 = 4 = 2²
⇒ 1 + 3 + 5 = 9 = 3²
⇒ 1 + 3 + 5 + 7 = 16 = 4²
⇒ 1 + 3 + 5 + 7 + 9 = 25 = 5²
⇒ 1 + 3 + 5 + 7 + 9 + 11 = 36 = 6²
⇒ 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49 = 7²
Class 6 WBBSE Math Solutions
Question 2. By arranging the buttons, let’s understand the relation between square and square root of natural numbers.
Solution:
By arranging the buttons, let’s understand the relation between square and square root of natural numbers.

Class 6 Math Solutions WBBSE Chapter 25 Fun With Numbers Exercise 25.1
Question 1. With four 4 ‘4s’, let us make numbers from 1 to 18.
Solution:
1. \(\frac{4+4}{4+4}=\frac{8}{8}=1\)
2. \(\frac{4}{4}+\frac{4}{4}=1+1=2\)
3. \(\frac{4+4+4}{4}=\frac{12}{4}=3\)
4. \(\frac{4-4}{4}+4=0+4=4\)
5. \(\frac{4+4 \times 4}{4}=-\frac{4+16}{4}=\frac{20}{4}=5\)
6. \(4+\frac{4+4}{4}=4+2=6\)
7. \(4+4-\frac{4}{4}=8-1=7\)
8. \(4+\frac{4 \times 4}{4:}=4+4=8\)
9. \(4+4+\frac{4}{4}=8+1=9\)
10. \(\frac{44-4}{4}=\frac{40}{4}=10\)
11. \(\frac{4}{4}+\frac{4}{4}=\frac{4 \times 10}{4}+1=11\)
12. \(\frac{44+4}{4}=\frac{48}{4}=12\)
13. \(\frac{44}{4}+\sqrt{4}=11+2=13\)
14. \(4(4-4)-4=14 \cdot 4-4=14\)
15. \(4 \times 4-\frac{4}{4}=16-1=15\)
16. \(4+4+4+4=16\)
17. \(4 \times 4+\frac{4}{4}=16+1=17\)
18. \(44 x \cdot 4+\cdot 4=17 \cdot 6+\cdot 4=18\)
Question 2. With five ‘9s’, let me make 1000.
Solution:
⇒ \(999+\frac{9}{9}=999+1000\)
Question 3. Let’s solve puzzles with Roman letters:
1. If 9 is taken from 6,10 is taken from 9,50 is taken from 40, we get 6 – let’s try now it can be made possible.
Solution:
⇒ If 9 is taken from 6 i.e., VI-IX = 0,
⇒ 10 is taken from 9 i.e., IX – X = 1
⇒ 50 is taken 40 i.e., XL – L = 2
∴ We get, with three match sticks I made VI.
2. By just shifting one match stick, let us get our answer correct.
Solution: As there are three sticks on both sides.
WBBSE Class 6 Maths Solutions
Question 4. There are 5 apples in a basket. Let’s divide them among 5 girls in such a way that each gets 1 apple but one apple remains in the basket.
Solution: If 4 girls get I apple each while the fifth girl gets the basket in the remaining apple still in it.
Question 5. Azim has 3 match sticks. He asked me to write 4 with those 3 match sticks. Let me try to do.
Solution: Azim has 3 match sticks I write 4 with 3 match sticks IV.
Question 6. I have 3 match sticks. I took 2 more sticks to write 8.
Solution: I have 3 match sticks. I took 2 more sticks.
⇒ Total number of sticks = 3 + 2 + 5
⇒ I write – VIII.
Question 7. I have 7 match sticks and 6 buttons. I arranged the 7 match sticks on a table in a form given below.
Solution:
⇒ If I start from 1, the next one will be 3.
⇒ I start with 2, the next one will be 4.
⇒ I start at 5, the next one will be 7.
⇒ I start from 6, and the next one will be 1.
⇒ The button I have placed already.
⇒ So, next can not start from button 6.
Question 8. Few other fun with match sticks:
1. With 6 match sticks I made 1/7 as 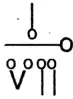
Solution:
With 5 match sticks I made \(\frac{1}{3} \text { as } \frac{1}{\text { III }}\)
WBBSE Class 6 Maths Solutions
2. Let’s make 2 fractions whose value is 1/3.
Solution:
With 6 match sticks I made \(\frac{2}{6} \text { as } \frac{11}{V 1}\)
Question 9. I have 12 match sticks. I shall make a puzzle with these 12 match sticks and try to solve them. With these 12 sticks, 4 squares (and a big square) have been found.
1. First removing 2 sticks, 2 different-sized squares are made.
Solution:
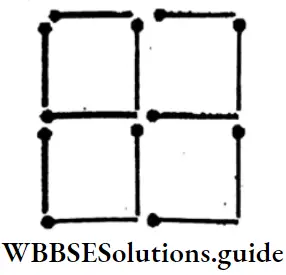
One small and one big squares.
2. By shifting 3 sticks, let’s try to get 3 equal-sized squares.
Solution:
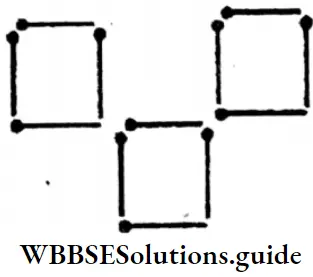
Three equal-sized squares
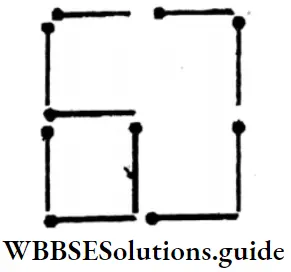
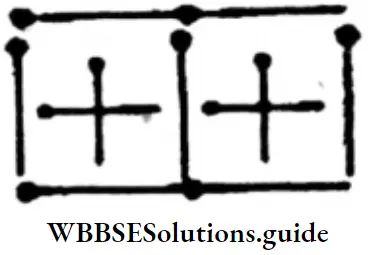
3. Again, by changing side of 4 sticks, 3 equal-sized squares can be formed
Solution:
Three equal-sized squares.
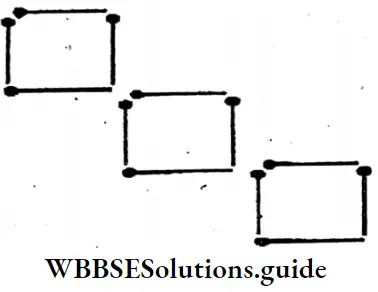
4. Just by moving 2 sticks, let’s try to get 7 different-sized squares. (In this case 2 sticks may be placed diagonally.)
Solution:
Seven different-sized squares.
WBBSE Math Solutions Class 6
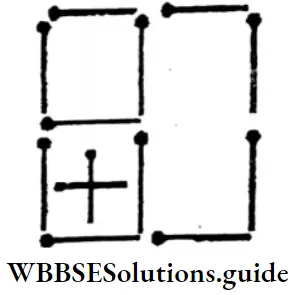
5. I moving 4 sticks, let’s try to make 10 small and big squares (but in this case 2 sticks can be put diagonally).
Solution:
10 small and big squares.
Question 10. We know 2 + 2 = 2 x 2 i.e., two 2’s added and two 2’s multiplied gives the same value.
1. For 3 natural numbers _____, _____, and _____, it is found that their sum is equal to their product. i.e., ____ + ______ + _______ = ______ x _______ x ________
Solution: 1 + 2 + 3 = 1 x 2 x 3
2. Let us find 4 natural numbers, whose sum and product are the same. i.e., ____ + ____ + ______+ ____ + ______ + _____ + _______ + _____
Solution: 1+1+2+4=1x1x2x4
3. Is it possible to have 5 natural numbers where this relation holds good ? (find myself) Yes, I can make the sum and product of 5 natural numbers are equal, one example is: 1+1+1+2+5=1x1x1x2x5
Let us try to find other numbers _____ + _____ + _____ + _____ + ______ = ______ x _______ x _______ x ________ x ________
Solution: 1 + 1 + 1 + 3 + 3 = 1 x 1 x 1 x 3 x 3
Question 11.
⇒ 1 x 1 = 1
⇒ 11 x 11 = 121
⇒ 111 x 111 = 12321
⇒ 1111 x 1111 = 1234321
_______ x _____ = ________
_________ x ______ = _______
Solution:
⇒ 1 x 1 = 1
⇒ 11 x 11 = 121
⇒ 111 x 111 = 12321
⇒ 1111 X 1111 = 1234321
⇒ 11111 X 11111 = 123454321
⇒ 111111 X 111111 = 12345654321
