Class 6 Math Solutions WBBSE Chapter 5 Concept Of Algebraic Variables
Example: To make 15 such triangles, let us find the number of match sticks required without actually forming the triangles.

Solution:
The number of match sticks required without actually forming the triangles Are
Total number of match sticks = 3 x Number of triangles.
If there are triangles, No. of match sticks required = 3n.

WBBSE Class 6 Maths Solutions Chapter 5 Concept Of Algebraic Variables Exercise 5.1
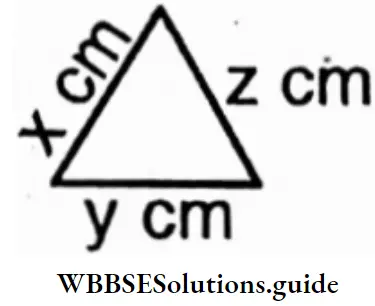
Question 1. Let us find the perimeter of the triangle in terms of x, y, and z.
Solution:
The perimeter of the triangle = x cm + ycm + z cm = (x+y+z) cm.
Read and Learn More WBBSE Solutions For Class 6 Maths
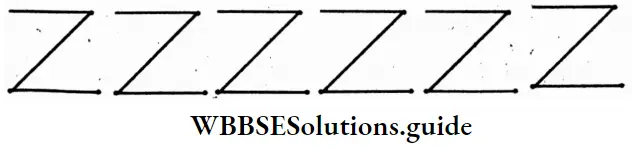
Question 2. Let me form the letters V, Z, E, D………with match sticks, as given below, and try to form a relation to find the total number of match sticks required for any of these figures.
Solution:
1. 
Total number of match sticks = 2x
2. 
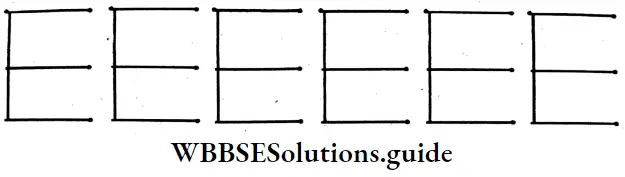
Total number of match sticks = 3x
3. 
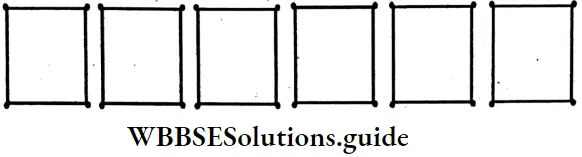
Total number of match sticks = 4x
4. 
Total number = 4x Where x = Number of sticks in V, Z, E, D.

Question 3. I am 4 years younger than my brother. If my brother’s age is x years, let me write my age in terms of my brother’s age.
Solution:
My brother’s age = x years
I am 4 years younger than my brother.
∴ My age = (x – 4) years.
| Class 6 History | Class 6 Social Science |
| Class 6 Geography | Class 6 Science |
| Class 6 Maths | Class 6 Science MCQs |
| Class 6 General Science | Class 6 Maths Solutions |
| Class 6 Geography | Class 6 Hindi |
My age in terms of my brother’s age is (x minus 4) years.
“WBBSE class 6 maths chapter 5 solutions”
Question 4. Rafika Begum and Aajma Khatoon are making garlands. Aajma Khatoon made 6 garlands more than Rafika Begum. Let us form a relation to find the number of garlands Aajma Khatoon made.
Solution:
Given
Rafika Begum and Aajma Khatoon are making garlands. Aajma Khatoon made 6 garlands more than Rafika Begum.
Let Rafika Begum made x garlands.
Aajma Khatoon made 6 garlands more than Rafika Begum.
∴ Aajma Khatoon made (x + 6) garlands.
Question 5. In our shop, there are many oil pastel color boxes. Each box has 12 pastel colours. Without counting, let us form a relation to find how many pastel colors are there in the shop.
Solution:
Given
In our shop, there are many oil pastel color boxes. Each box has 12 pastel colours.
Let there are x number of colour boxes.
Each box contains 12 pastel colors.
∴ Number of total pastel colours in the shop = 12 x.
Question 6. Today at a program of our school we seated ourselves in many rows. In each row there are 15 students. Let us form a relation to find the total number of students seated in the program of our school.
Solution:
Given
Today at a program of our school we seated ourselves in many rows. In each row there are 15 students.
Let there are x number of rows in the school. In each row there are 15 students.
∴ Total number of students = 15x.
“concept of algebraic variables WBBSE class 6 maths”
Question 7. Sitting beside a pond, Partha and Tirtha, both were trying to catch fish. Partha caught 5 fishes more than Tirtha. Let us express the number of fishes caught by Partha in terms of the number of fishes caught by Tirtha.
Solution:
Given
Sitting beside a pond, Partha and Tirtha, both were trying to catch fish. Partha caught 5 fishes more than Tirtha.
Let Tirtha caught x number of fishes. Partha caught 5 fishes more than Tirtha.
∴ Partha caught (x – 5) fishes.
Class 6 Maths Solutions WBBSE
Question 8. Mita and Maya are making paper boats. Mita made 2 boats less than Maya. Let us form a relation to find the number of boats made by Mita.
Solution:
Let Maya made x number of boats. Mita made 2 boats less than Maya.
∴ Mita made (x – 2) boats.
Question 9. Father bought several packets of sweets. If each packet contains 5 sweets, let us form a relation to find the total number of sweets bought by the father.
Solution:
Let father buy x packets of sweets. Each packet contains 5 sweets.
∴ Total number of sweets father bought = 5x.
Question 9. Grandmother prepared coconut sweets today. She gave my brother 2 more sweets than she gave me and my sister 3 less. Let us form a relationship to find how many sweets my brother and sister got in terms of the unknown number of sweets I got.
Solution:
Let I get x number of sweets.
My brother got (x + 2) sweets.
My sister got (x – 3) sweets.
“WBBSE class 6 maths chapter 5 important questions”
Question 10. In the expressions given below, let us identify the variables and constants:
1. x + 2
Solution: x + 2 — variable x Constant 2
2. 5
Solution: 5 – Constant 5
3. y – 6
Solution: y-6 – variable y Constant6
4. 2p + 8
Solution: 2p + 8 – variable p – Constant 2, 8
5. -4
Solution: – 4 – Constant 4
6. 5 (3x – 2) + 5
Solution: 5 (3x-2)+5 – variable x – Constant 5, 3, – 2
7. 10-2p
Solution: 10p-2 – variable p – Constant 10,-2
8. 15z
Solution: 15z – variable z – Constant 15
9. x + 2y
Solution: x + 2y – variable x,y – Constant 2
“what are algebraic variables class 6 WBBSE”
Question 11. Let us express in language the following expressions:
1. y + 6
Solution: Sum of y and 6
2. a-2
Solution: Difference of a and 2
3. 5y
Solution: 5 times of y or y is multiplied by 5
4. a/9
Solution: a is divided by 9
5. 3x
Solution: 3 times of x or x is multiplied by 3
6. 5x+2
Solution: Sum of 2 and 5 times of x
7. a+b
Solution: Sum of a and b
8. 6x-4
Solution: Difference of 6 times of x and 4
9. x>5
Solution: x is greater than 5
10. x≥7
Solution: x is greater than or equal to 7
11. y ≯ 10
Solution: y is not greater than 0
12. y≤10
Solution: y is less than or equal to 10
13. x ≮ 7
Solution: x is not less than 7
14. x<9
Solution: x is less than 9
15. x≥12
Solution: x is greater than or equal to 12
16. x≥5
Solution: x is not greater than 5
Forming expressions with signs and symbols

Solution:
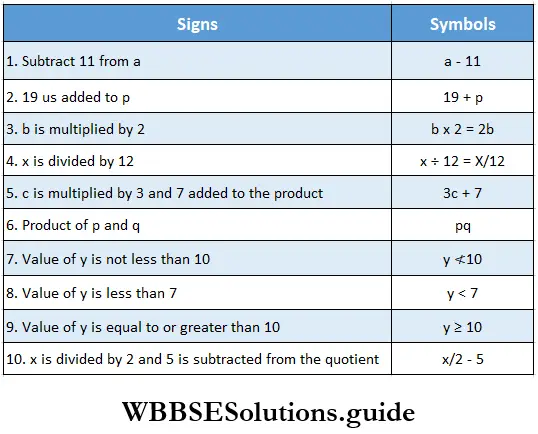
Chapter 5 Concept Of Algebraic Variables, Exercise 5.2
Question 1. Let us write in language the following expressions.
1. 10a
Solution: Ten times of a or a is multiplied by 10
2. a + c
Solution: Sum of a and c
3. x – y
Solution: Difference of x and y
4. 9x + 2
Solution: Sum of 9 times of x and 2
5. x + y + z
Solution: Sum of x, y and z
6. 3 x – 7
Solution: Seven less than three times of x
7. p/3-4
Solution: Four less than one-third of p
8. x > 6
Solution: x is greater than 6
9. p ≯ 9
Solution: p is not greater than 9
“difference between constants and variables in algebra”
Question 2. Let us form the algebraic expressions of the following with signs and symbols
1. Sum of a and 7
Solution: a + 7
2. Subtract 9 from y
Solution: y – 9
3. Multiply a by 3
Solution: 3a
4. x is greater than 13
Solution: x>13
5. y is not equal to 5
Solution: y ≠ 5
6. x is divided by 8
Solution: x/8
7. Sum of ten times p and 7
Solution: 10p + 7
8. 8 is subtracted from 3 times x
Solution: 3x – 8
9. Sum of x and y
Solution: x + y
10. Product of x and y
Solution: x X y
11. k is less than y
Solution: k < y
12. b is not less than 8
Solution: b ≮ 8
“how to form algebraic expressions using variables”
Question 3. Let us find the difference between the following sets of algebraic expressions:
- x+5, x-5, 5x
- 2p+3, 2p-3, 3p+2, 3p-2
Solution:
1. x+5 → Sum of x and 5
x- 5 → 5 is subtracted from x
5x → 5 times of x
2. 2p + 3 → Sum of twice p and 3
2p – 3 → 3 less than twice of p
3p + 2 → Sum of times of p and 2
3p – 2 → 2 less than 3 times of p
3. Let us prepare four different algebraic expressions with the variable x and constant 6. Let us write in a statement the expressions formed and find the difference amongst them :
Solution:
Four algebraic expressions x + 6; x – 6, 6x + 2 ; 6x – 2
x + 6 → Sum of x and 6
x – 6 > Difference of x and 6
6x + 2 > Sum of six times of x and 2
6x – 2 > Difference of six times of x and 2
4. Let us prepare four different algebraic expressions with the variable x and two different constants 9 and ![]()
Solution:
Four different algebraic expressions with variable x and two different constants 9 and 11.
9X + 11 → Sum of nine times of x and 11
11X —9 → Difference of 11 times x and 9
9x X 11 → Product of 11 and nine times of x
9 ÷ 11x → Nine divided by 11 times of x
5. With two variables and one constant, let us prepare four different expressions and find the difference among them
Solution:
Four different algebra expression with two variables and one constant. 2x + y + 1, 2x + 1 – y, 2y + x + 1, 2y + 1 – x
2x + y + 1 → Sum of twice x and y and 1
2x + 1 – y → y is subtracted from the sum of twice x and 1
2y + x + 1 → Sum of twice y and x and 1
2y + 1 – x → x is subtracted from the sum of twice y and 1.
Problem 4. Let us match the two sides
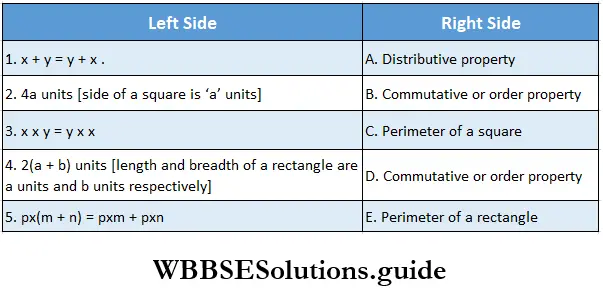
Solution: 1. B, 2. C, 3. D, 4. E, 5. A
Question 5. Let us read and fill in the gaps
1. Present age of Mukti is x years, 4 years later her age will be ![]() years.
years.
Solution:
Present age of Mukti is x years, 4 years later her age will be [x + 4] years.
2. Present age of Firoz is y years; 7 years ago his age was ![]() years.
years.
Solution:
Present age of Firoz is y years; 7 years ago his age was [y- 7] years.
3. In Kumud’s garden there are x number of saplings of marigold. But in Shahida’s garden, there are three times more saplings than Kumud’s garden. There are ![]() saplings in Shahid’s garden.
saplings in Shahid’s garden.
Solution:
In Kumud’s garden there are x number of saplings of marigolds. But in Shahida’s garden there are three times more saplings than Kumud’s garden. There are [3x] saplings in Shahida’s garden.
4. Funds were collected for repairing the roads of Durganagar. Habib paid Rs. x but Muskan paid Rs. 10 more than twice the money Habib paid. Muskan paid Rs ![]() .
.
Solution:
Funds were collected for repairing the roads of Durganagar. Habib paid Rs. x but Muskan paid Rs. 10 more than twice the money Habib paid. Muskan paid Rs. [2x + 10].
5. The height of David is 3 cm less than Aminur. If height of Aminur is ‘x’ cm, height of David is ![]() cm.
cm.
Solution:
Height of Devid is 3 cm less than Aminur. If the height of Aminur is ‘x’ cm, height of David is [x- 3] cm.
Problem 6. Let us prepare stories which will satisfy the following expressions
1. Rs. (x + 18)
Solution:
∴ price of my exercise book is Rs. x. Price of Mihir’s exercise book is Rs.18 more than mine. Hence, price of Mihir’s exercise book is Rs. (x + 18).
“basic operations on algebraic variables class 6 maths”
2.(y — 21) cm.
Solution:
∴ Length of my classroom is y cm, but the length of another room is 21 cm less than my classroom. So the length Of the other room is (y – 21) cm.
3. 5x years
Solution:
My sister’s age is x years and I am 5 times older than her.
∴ My age is 5x years.
“examples of algebraic variables in real life WBBSE”
4. p/4
Solution:
A man bought p cakes, his 4 boys, each boy got p/4.
5. (2x + 3) metres
Solution:
The length of a room is x m but the length of another room is 3 m more than the twice of the 1st room.
∴ The length of 2nd room is (2x + 3) metres.
6. (3 x – 5) hours
Solution: A boy took x hours to do all the sums of an exercise but his friend took 5 hours less than thrice of the time taken by the 1 st boy.
∴ So, the 2nd boy took (3x – 5) hours to do the sums.
