WB Class 7 Math Solution Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2 Solved Problems
Natural numbers: 1, 2, 3, 4, 5, …… are counting numbers or natural numbers such that 1 is the first natural number and there is no last natural number.
⇒ The natural numbers is denoted by N and is written as N = (1, 2, 3, 4, )
Whole numbers: The numbers 0, 1, 2, 3, . . . . . . . are called whole numbers.
⇒ The whole numbers is denoted by w and is written as w= (0, 1, 2, 3. . . . . .
Integers: The numbers……., -4, -3, -2, -1, 0, 1, 2, 3 ……. are called integers. The integers is denoted by z and is written as z = (…, -3, -2, -1, 0, 1, 2, 3 …)
⇒ The integers greater than 0, i.e 1, 2, 3,…. are called positive Integers and the integers less than 0, i.e. -1, -2, -3, . . . . are called Negative Integers.
⇒ 0 (zero) is an integer that is neither positive nor negative.
Read and Learn More WBBSE Solutions for Class 7 Maths
Addition:
Question 1. Add with the help of a number line
1. {(+3) + (-5)} + (-10)
2. {(+3) + {(-5)+(-10)}
Solution:
1. {(+3)+(-5)) + (-10)
Wbbse Class 7 Maths Solutions
⇒ {(+3)+(-5)}+(-10)=-12
2. (+3)+ {(-5)+(-10)}
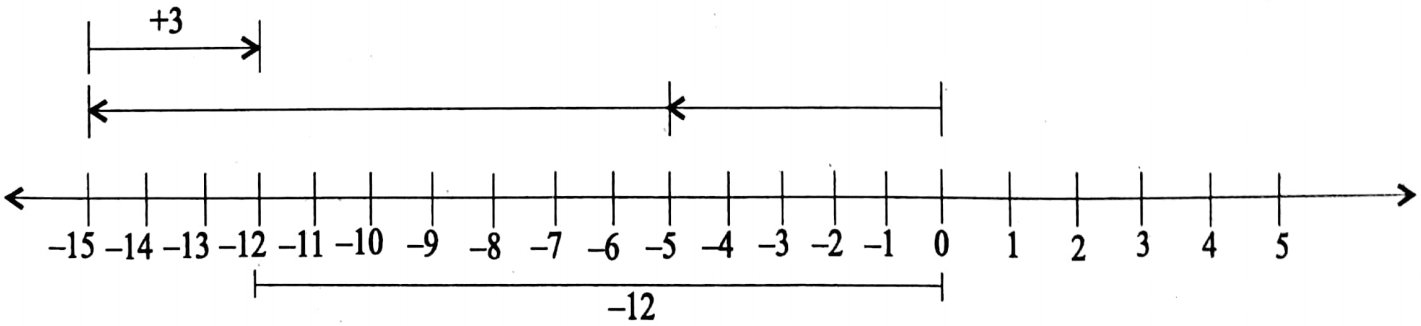
⇒ (+3)+{(-5)+(-10)}=-12
⇒ From (1) and (2), we can write,
⇒ {(+3)+(-5)}+(-10)= (+3) + {(-5)+(-10)}
These integers follow the associative law of addition.
WB Class 7 Math Solution Subtraction
Question 1. Subtraction by using the number line
1. {(+4) (-7)}-(-6)
2. (+4) {(-7)-(-6)}
Solution:
1. {(+4) (-7)} – (-6)= {(+4) + (+7)} + (+6)
Wbbse Class 7 Maths Solutions
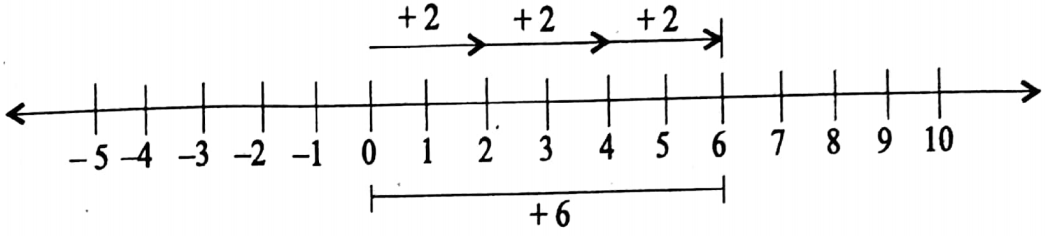
= {(+4) – (-7)} – (-6)} = +17
2. (+4) – {(-7) – (-6)}
= (+4) – {(-7) + (+6)}
= (+40 + {(+7) + (-6)}
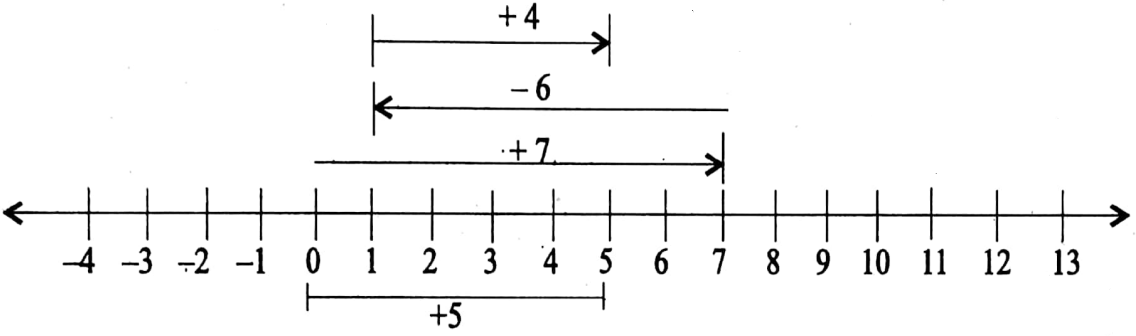
So (+4) – {(-7)-(-6)} = +5
Hence from (1) and (2), we can write
{(+4) (-7)}-(-6) ≠(+4) – {(-7) – (-6)}
Wbbse Class 7 Maths Solutions
Thus subtracting on the number line we found that for the subtraction of integers, the law of association does not hold.
Multiplication
Question 1. Multiply with the help of a number line
1. (+3) × (+2)
2. (+3) × (-2)
3. (-3) × (-2)
Solution:
1. (+3) x (+2) = (+3)+(+3)
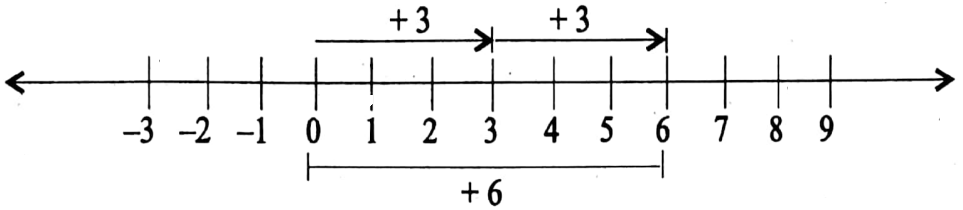
⇒ (+3) x (+2) = +6
⇒ (+2) x (+3) = (+2) + (+2)
Wbbse Class 7 Maths Solutions
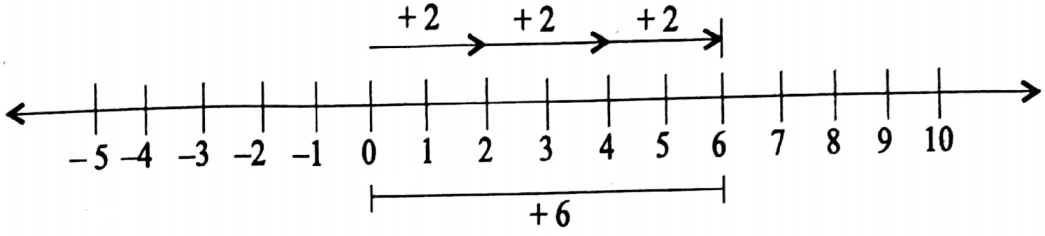
(+2) × (+3)= +6
So (+3) x (+2) = (+2) x (+3)
Hence two integers follow the commutative law of multiplication.
2. (+3) x (-2) = (-2)+(-2)+(-2)
(+3) x (-2) = -6
3. (-3) x (-2) = {(-2)+(-2)+(-2)}
Wbbse Class 7 Maths Solutions
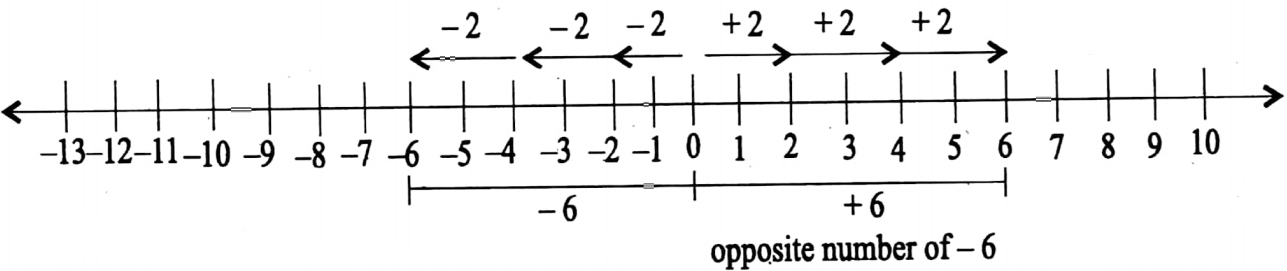
(-3) x (-2) = +6
WB Class 7 Math Solution Divide
Question 1.(-24) ÷ {(-2)+8}
2. (-24)÷ (-2)+(-24) ÷ 8
Solution:
Given
1. (-24) ÷ {(-2) + 8}
= (-24)÷ 6
=-4
(-24) ÷ {(-2) + 8} =-4
2. (-24)÷ (-2)+(-24) ÷ 8
= (+12) + (-3)
= +9
(-24)÷ (-2)+(-24) ÷ 8 = +9
So (-24) ÷ {(-2)+8) ≠ (-24)÷ (-2) + (-24) ÷ 8
Thus distributive law does not hold for the division of numbers (excluding zero).
Such important points: For a nonzero integers a, b, c
1. a + (b + c) = (a + b) + c [Associative law of addition ]
2. a x (b x c) = (a x b) x c [Associative law of multiplication]
3. a x (b+c) = a x b+a x c [Distributive law of multiplication]
4. a – (b – c) ≠ (a – b) -c
5. a ÷ (b + c) ≠ a ÷ b + a ÷ c
6. a+b=b+ a [Commutative law of addition]
7. a – b ≠ b – a
Wbbse Class 7 Maths Solutions
8. a x b = b x a [Commutative law of multiplication]
9. a ÷ b ≠ b ÷ a
Question 1. Choose the correct answer
1. The value of (-3)+(-4)+(+10) is
1. – 17
2. +3
3. – 10
4. +9
Solution:
Given
(-3)+(-4)+(+10)
= (-7) + (+10)
= +3
So the correct answer is 2. +3
2. The value of (-15) – {(+3) + (-7)} is
1. -11
2. -19
3. +11
4. +19
Solution:
Given
(-15) – {(+3) + (-7)}
= (-15) – (-4)
= -15 + 4
= -11
So the correct answer is 1. -11
3. The value of (-24) ÷ (+4) × (-3) is
1. +2
2. -2
3. +18
4. -18
Solution:
Given
(-24) ÷ (+4) x (-3)
= (-6) × (-3)
= +18
So the correct answer is 3. +18
Wbbse Class 7 Maths Solutions
Question 2. Write ‘true’ or ‘false’
1. The value of (-6) x (-5) x (-7) x (+3) is -630
Solution:
Given
(-6) × (-5) × (-7) × (+3)
= (+30) × (-21)
=-630
So the statement is true.
2. The value of (-4) ÷ (-2) x (+2) – (+4) is 0
Solution:
Given
(-4) ÷ (-2) x (+2) – (+4)
= (+2) x (+2) – (+4)
= (+4) – (+4)
= 0
So the statement is true.
3. The value of (-15)+(-5) of (+3) x (-4) is 4
Solution:
Given
(-15)÷(-5) of (+3) x (-4)
= (-15)÷(-15) x (-4)
= (+1) × (-4)
=-4
So the statement is false.
Question 3. Fill in the blanks
Wbbse Class 7 Maths Solutions
1. The value of (-18) + 
+3=-6
Solution: (-18)÷ +3=-6
⇒ (-18)÷ =-6 -3
⇒ (-18) ÷ = -9
⇒ 
⇒ = \(\frac{-18}{-9}\) = +2
2. x (-1) + 9 = 0
Solution: × (-1) + 9 = 0
⇒ × (-1) = -9
⇒ = \(\frac{-9}{-1}\) = 9
3. (-11) x (-9) x (-5) × (-6) × (-3) =
Solution: (-11) x (-9)-x (-5) x (-6) x (-3)
= (+99) x (+30) x (-3)
= (+2970) × (-3)
= – 8910.
Question 4. Verify, if the distributive law of multiplication holds for integers in the following cases.
1. (-3) x (8+ 4)
2. (-4) x {(-6) + (+3)}
Solution:
1. (-3) x (8 + 4)
= (-3) x (12)
=-36
(-3) x (8 + 4)
= (-3) x (8) + (-3) x (4)
= (-24) + (-12)
-36
∴ (-3) x (8+4)=(-3) x (8) + (-3) x (4)
2. (-4) x {(-6) + (+3)}
=(-4) (-3)
= + 12
(-4) x (-6) + (-4) x (+3)
= (+24) + (-12)
= + 12
∴ (-4) × {(-6) + (+3)} = (-4) x (-6) + (-4) x (+3)
Question 5. Divide
1. (-275) ÷ (-25)
2. (-150)÷(+15)
Solution:
1. (-275) ÷ (-25)= +11
2. (-150)÷(+15)=-10
WB Class 7 Math Solution Addition Subtraction Multiplication And Division Of Integers
Addition Subtraction Multiplication And Division Of Integers Exercise 4.1
Question 1. From the number line, let us write the predecessor (just before) and successor(just after) of the integers given below:
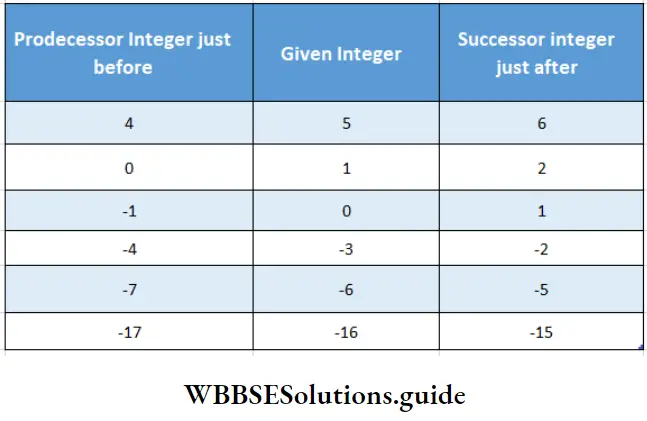
Solution:
- For the addition of 2 positive integers on the number line, from the position of the first integer one has to move further right.
- For the addition of 2 negative integers on a number line, from the position of the first integer one has to move further left.
- For subtraction of 2 positive integers on a number line, from the position of the first integer one has to move to the left.
- For subtraction of 2 negative integers on a number line, from the position of the first integer one has to move to the left.
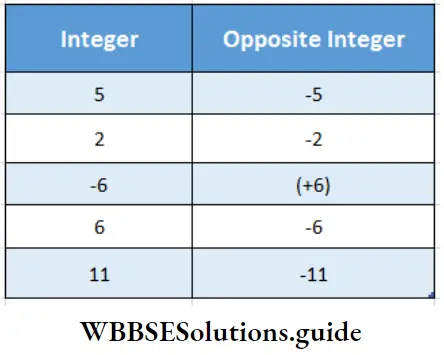
Question 2. Let us complete the table given below:
Solution:
Question 3. Let’s fill up the chart below, with the steps followed by chhotu along the stairs.
Solution:
Question 4. Let us complete the chart below for Manai going up or down along the numbered steps of the stair
Solution:
Addition Subtraction Multiplication And Division Of Integers Exercise 4.2
Question 1. Let us match the two sides verifying the laws :
Solution:
(1) — (2) : (2)- (3) – (4)– (5)- (1)
Question 2. Let us write a negative integer which is the sum of two negative integers.
Solution:
(- 7) = (- 5) + (- 2)
Question 3. Let us write a negative integer which is the difference of two positive integers.
Solution:
(-15) = (+ 6) -(+21)
Question 4. Let us write such a negative integer which is the difference of two negative integers.
Solution:
(-12) = (- 32) – (- 20)
Class 7 Math Solution WBBSE Addition Subtraction Multiplication And Division Of Integers Exercise 4.3
Question 1. 6 x (-8)
Solution :
6 × (-8) = (- 8) + (- 8) + (- 8) + (- 8) + (- 8) + (- 8) = 48 = – (6 × 8)
Question 2. 7 × (-3)
Solution :
7 × (-3) = (- 3) + (- 3) + (- 3) + (- 3) + (- 3) + (- 3) + (- 3) = – 21
= -(7×3)
Question 3. 9 × (- 12)
Solution :
9 × (- 12) = (- 12) + (- 12) + (- 12) + (- 12) + (- 12) + (- 12) + (- 12) + (-12) + (-12)
= -108
= – (9 × 12)
Question 4. (- 4) x 3
Solution :
(- 4) x 3 = 4 x (- 3)
= – 12
Question 5. 6 x (- 8)
Solution :
6 x (- 8) = 8 x (- 6) = – 48
Question 6. 7x(-3)
Solution:
7x(-3)= (- 7) x 3 = – 21
Class 7 Math Solution WBBSE Addition Subtraction Multiplication And Division Of Integers Exercise 4.4
Question 1. Let’s find the value of (- 5) × (- 2) starting from (- 5) × 2
Solution:
Given
⇒ (- 5) × 2 =-10
⇒ ( -5) × 1 = 10-(-5) = -10 + 5 = – 5
⇒ (- 5) × 0 = -5-(-5) =-5 + 5 = 0
⇒ ( 5) × (-1)= 0 – (-5) = 0 + 5 = 5
⇒ ( 5) × (-2)= 5 – (-5) = 5 + 5 = 10
⇒ (- 5) × (-2)= 5 – (-5) = 5 + 5 = 10
Question 2. Let’s find the value of (- 7) × (- 3) starting from (- 7) × 3
Solution:
Given
⇒ (- 7) × 3 = – 21
⇒ (- 7) × 2= -21 -(-7)= – 1 4 – (- 7)= – 21 + 7= -14 =
⇒ (- 7) × 1 = – 1 4 – (- 7)= – 14 + 7= -7
⇒ (- 7) × 0 = – 7 – (- 7)= -7 + 7= 0
⇒ (- 7) × (- 1) = 0 – (- 7)= 0 + 7= 7
⇒ (- 7) × (- 2) = 7 – (- 7)= 7 + 7 = 14
⇒ (- 7) × 3 = 1 4 – (- 7)= 14 + 7 = 21
Question 3. Let s find the value of (- 6) × (- 4) starting from (- 6) × 2
Solution :
Given
⇒ (- 6) × 4 = – 24
⇒ (-6) × 3 = – 24 – (- 6)= – 24 + 6= – 18
⇒ (- 6) × 2 = -18 -(-6)= – 18 + 6= -12
⇒ (- 6) × 1 = -12-(- 6)= -12 + 6= – 6
⇒ (- 6) × 0 = (- 6) – (- 6)= – 6 + 6 = 0
⇒ (- 6) × (- 1 ) .= 0 – (- 6)= 0 + 6= 0= 6
⇒ (- 6) × (- 2)= 6 – (- 6)= 6 + 6= 12
We know if a and b are integers then (- a) × (- b) = ab.
4. (- 7)× (- 9) = 63
5.(- 2) × (- 33) = 66
6. 0 × (- 6) = 0
7.(- 12) × (- 3) = 36
8. (- 7) × 0 = 0
Addition Subtraction Multiplication And Division Of Integers Exercise 4.5
Question 1. Let’s complete the table given below:
Solution:
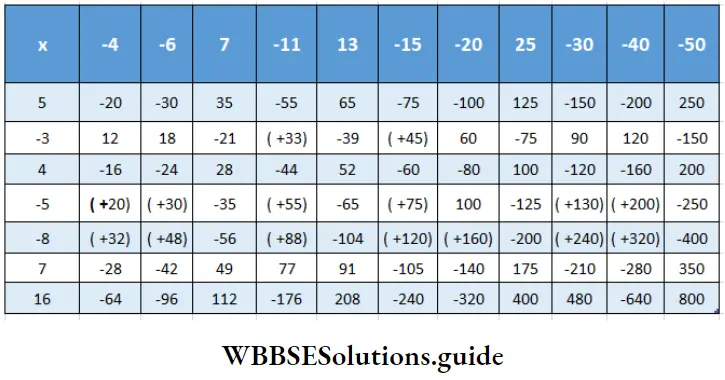
Question 2. (- 7) × 7 + 12 x (- 8)
Solution:
(- 7) × 7 + 12 x (- 8) = – 49 – 96
= -145
(- 7) × 7 + 12 x (- 8) = -145
Question 3.(- 20) × 11 + (- 35) × 20
Solution:
(- 20) × 11 + (- 35) × 20 = – 220 – 700
= -920
(- 20) × 11 + (- 35) × 20 = -920
Question 4.(- 8) × 45 + (- 6) × 12
Solution:
(- 8) × 45 + (- 6) × 12 = -120 – 72
= -192
(- 8) × 45 + (- 6) × 12 = -192
Question 5. 4 × (- 4) + (- 5) × 5
Solution:
4 × (- 4) + (- 5) × 5 = – 1 6 – 25 =- 41
4 × (- 4) + (- 5) × 5 =- 41
Question 6. (- 6) × (- 10) + (- 4) × 4
Solution:
(- 6) × (- 10) + (- 4) × 4 = + 60 – 16= 44
(- 6) × (- 10) + (- 4) × 4 = 44
Question 7. (- 9) × 3 + 7 x (- 4)
Solution:
(- 9) × 3 + 7 x (- 4) = – 27 – 28
= -55
(- 9) × 3 + 7 x (- 4) = -55
Addition Subtraction Multiplication And Division Of Integers Exercise 4.6
Question 1. (- 6) × (- 5) × (- 7) × (- 3)
Solution:
(- 6) × (- 5) × (- 7) × (- 3) = 30 × (- 7) × (- 3) = -210 × (- 3) = 630.
(- 6) × (- 5) × (- 7) × (- 3) = 630.
Question 2. (- 5) × (- 2) × (- 10) x (- 8) × (- 3)
Solution:
(- 5) × (- 2) × (- 10) x (- 8) × (- 3) = 10 x (- 10) × (- 8) x (- 3)
= 1 00 × (- 8) × (- 3) = 800 × (- 3) =-2400.
(- 5) × (- 2) × (- 10) x (- 8) × (- 3) = -2400.
Question 3. (- 11) × (- 12) (- 2)
Solution:
(- 11) × (- 12) (- 2) = 1 32 × (- 2) = – 264.
(- 11) × (- 12) (- 2) = – 264.
Question 4. (- 11) × (- 9) × (- 5) × (- 6) × (- 3)
Solution:
(- 11) × (- 9) × (- 5) × (- 6) × (- 3) = 99 × (- 5) × (- 6) × (- 3)
= – 495 × (- 6) × (- 3) = 2970 × (- 3) = – 8910.
(- 11) × (- 9) × (- 5) × (- 6) × (- 3) = – 8910.
Question 5. Let’s complete the chart below and write our decision.
Solution:
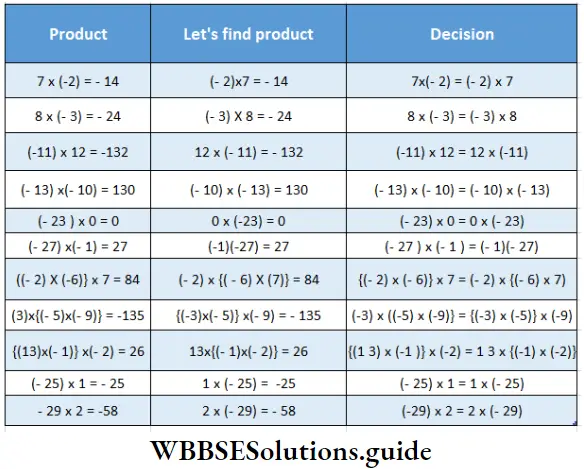
Addition Subtraction Multiplication And Division Of Integers Exercise 4.7
Question 1. 9 × (8 + 3) ______ 19 × 8 + 9 × 3 [Let’s put = / ≠]
Solution :
9 × (8 + 3) = 9 × 8 + 9 x 3
Question 2. 6 × (5 +4)______ 6 × 5 + 6 × 4 [Let’s put = / ≠]
Solution:
6 × (5 + 4) = 6 × 5 + 6 × 4
Class 7 Math Solution WBBSE Addition Subtraction Multiplication And Division Of Integers Exercise 4.8
Question 1. Mizanoor, Tirtha and Nafura appeared for an examination, there were 1 0 Questions in the examination. In this examination, one will get 5 marks for each correct answer and – 2 marks for each incorrect answer.
1. Mizanoor has got 6 correct and the rest 4 incorrect answers.
Solution :
Mizanoor obtained = 6×5 + 4 ×(-2)
= 30 – 8 – 22 marks.
2. Tirtha has got 5 correct and the remaining 5 incorrect answers.
Solution:
Tirtha obtained = 5 × 5 + 5 (- 2)
= 25 – 10 = 15 marks.
3. Nafura has got 3 correct and the remaining 7 incorrect answers.
Solution :
Natura obtained = 3 × 5 + 7 (- 2)
= 15 – 14 = 1 marks.
Question 2. In a furniture shop, 15 wooden almirahs were sold in a month, from 10 almirahs, there was a profit of Rs. 300 per almirah, But for the remaining 5 almirahs there was a loss of Rs. 200 per almirah. What is the profit or loss of the shop owner for the month, let’s find out.
Solution :
Given
In a furniture shop, 15 wooden almirahs were sold in a month, from 10 almirahs, there was a profit of Rs. 300 per almirah, But for the remaining 5 almirahs there was a loss of Rs. 200 per almirah.
Total profit from 10 almirahs = 10 × Rs. 300 = Rs. 3000.
Total loss from 5 almirahs = 5 × Rs. 200 = Rs. 1 000.
Total profit in this month by 15 almirahs
= Rs. 3000 – Rs. 1000 = Rs. 2000.
Question 3. In another mine, the lift goes down 4 m in every one minute.
1. What will be the position of the lift after an hour, Let’s find.
Solution:
In 1 hour i.e in 60 minutes it goes down
= 4 60 = 240 m.
2. If the lift starts from 15m above the ground, let’s find the position
of the lift after 30 mins.
Solution: In 30 min, the lift will go down = 4 × 30 = 120 m.
As the lift starts from 1 5 meters above the ground
∴ After 30 minutes the position of the lift will be
{(- 1 20 m) + 1 5 m} = -1 05 m i.e 1 05 m below
Addition Subtraction Multiplication And Division Of Integers Exercise 4.9
Question 1. 16 ÷ {(-4)4-2} ≠ 16 ÷ (-4) – 16 ÷ 2
Solution :
L H S = 1 6 -s- {(-4) 4- 2} = 1 6 + (- 2) = – 8
RHS = 16 ÷(-4)4-16÷2 = -4 + 8 = +4
∴ LHS ≠RHS
Question 2. (- 70)- {(7) – (- 5)} ≠ (- 70) + (7) + (- 70) ÷ (- 5)
Solution :
L H S = (- 70) ÷ {(7) > (- 5)} = – 70 ÷ 2 = – 35
R H S = (- 70) + 7 + (- 70) + (- 5) = – 10 + 14 = 4
= 14 = 4
∴ LHS ≠ RHS
Addition Subtraction Multiplication And Division Of Integers Exercise 4.10
Question 1. Let’s Calculate the values mentally :
1. (- 10) × 4 = ________
Solution:
(- 10) × 4 ________
= (- 10) × 4 =-40
2. ( – 15) × ________= -90
Solution:
( – 15) × ________= 90
= ( – 15) × 6= -90
3. 25 × ________= – 125
Solution:
25 × ________= – 125
= 25 ×(-5) = -125
4. (- 16) x ________= 96
Solution:
(- 16) x ________=96
(- 16) x 6 = 96
5. (-13)× ________ =-104
Solution:
(-13) × ________ =-104
(-13) x 8 =-104
6. ________21 =-126
Solution:
_______21 =-126
– 6 × 21 = -126
7. ________=-42
Solution:
________=-42
14 × -3 = -42
8. ________ (- 30) = 330
Solution:
________ (- 30) = 330
-11 × (- 30) = 330
9. (-26) + ________=1
Solution:
-26 + ________=1
-26 ÷ -26 =1
10. ________ = – 29
Solution:
________ = – 29
29 ÷ 1 = – 29
11. ________+ (- 59) = – 1
Solution:
________+ (- 59) = – 1
59 ÷ (- 59) = -1
12. 87 ________= – 87
Solution:
87 ________= – 87
87 ÷ -1= -87
Question 2. In an examination Joseph answered 15 questions, of which 9 answers were correct but the remaining 6 were incorrect- If he gets 5 marks for each correct answer and his total is 33, let’s find, the marks allotted for incorrect answers in the examinations.
Given
In an examination Joseph answered 15 questions, of which 9 answers were correct but the remaining 6 were incorrect- If he gets 5 marks for each correct answer and his total is 33
The total marks obtained by Joseph is 33
He got 5 marks for each of his 9 correct answers
Marks for his correct answer 9 × 5 45
For a wrong answer, his marks are reduced by
= (45 – 33) marks = 12 marks
For 6 incorrect answers, his marks were reduced by 12 marks
For 6 incorrect answers, he got = – 12
Marks for 1 incorrect answer is (- 12) + 6 = – 2. (Solution: )
Question 3. Rehana and Sayan both appeared for an examination & each of them will have to answer 12 questions
1. Rehana got 36 marks in total by answering 8 questions correctly and the remaining 4 questions incorrectly. If she got 6 marks for each correct answer, let’s find the total marks obtained by him.
2. Let’s find the total marks obtained by Sayan if he answered 6 questions correctly and 6 questions answered incorrectly.
Solution :
Rehana got for eight correct answer = 6 × 8 = 48 but she got less (48 – 36) = 1 2 for 4 wrong answer
Marks for each wrong answer = 12 ÷ 4 = 3.
In the case of Sayan :
For 6 correct answer, he got = 6 × 6 = 36 & marks deducted for 6 wrong answer = 6 × 3 = 18
∴ Sayan obtained = 36 – 1 8 = 18 marks.
Question 4. The temperature of a certain place is 12° C The temperature reduces uniformly in every hour and reaches – 4°C after 8 hours. Let’s find the rate of reduction of temperature per hour.
Solution:
Given
The temperature of a certain place is 12° C The temperature reduces uniformly in every hour and reaches – 4°C after 8 hours.
Total temperature reduced in 8 hours = 12°C -(-4°C)= 16°C
16°C
∴ Rate of reduction of temperature per hour = \(\frac{16^{\circ}}{8}\) = 2°C
Question 5. A lift in a mine moves down 24 m in 8 mins. If it moves in a uniform rate, let’s find at what distance below the surface, it will be after 6 mins. If the lift starts from a height of 10 m above the ground, let’s find how deep the lift will go from the surface after 70 mins.
Solution:
Given
A lift in a mine moves down 24 m in 8 mins. If it moves in a uniform rate, let’s find at what distance below the surface, it will be after 6 mins. If the lift starts from a height of 10 m above the ground
The lift moves down 24 meter in 8 min.
∴ In 6 minutes it moves down = \(\frac{24}{8}\) × 6 m = 18 meters.
Again the lift moves down in 70 minutes = \(\frac{24}{8}\) × 70 m = 21 0 meters.
As it is 10 m above the ground, so in 70 min. the lift will go down
from the surface = (21 0 – 1 0) m = 200 meter.
Question 6. Let us fill up the blank squares:
1. – 16 ÷ (-2) +________ = -1
Solution : or, = – 1 – 8 = – 9
∴ 8 + – 9 = – 1.
2. 20 – 50 + ___________ = – 1
Solution :
Or, ___________= – 1 + 30
= 29
∴ -30 + 29 = – 1.
3. 41 × (- 5) + = – 3
Solution:
Or. _______ = – 3 + 205 = 202
∴ 205 + 202 = – 3
4. (-9)×(-3)×_______= -81
Solution :
Or, ________ = (- 81 ) ÷ 27 = – 3
Or, 27 × _____________ = 81
∴ (- 9) × (- 3) × – 3 = – 81
5. (-15) ÷ (-5)- ______ = -1
Solution:
Or, 3 – = – 1
Or, 3 + 1 = ______ ie, ________= 4
∴ (-15) ÷ (- 5) -__________ = – 1
6. (-18) ÷ ___________+ 3 = -6
Solution:
Or, – 18 ÷ _______ = – 6 – 3 = – 9
Or, (-18) ÷ (-9) = 2
∴ (-18) – 2 + 3 = -6
7. ______ ÷ 4 – 2 = – 7
Solution :
Or, _________ 4 – 2 = – 7 + 2 = – 5
Or , ________= – 5 x 4 = – 20
∴ – 20 ÷ 4 – 2 = -7
8. ___________ ×(-1) + 9 = 0
Solution :
Or, × (- 1 ) = – 9
Or, = (- 9) ÷ (- 1) = 9
∴ 9 ×(- 1) + 9 = 0
Question 7. Let us take 2 examples to show that the cumulative law holds in case of multiplication but does not hold for the division of integers. Solution :
1. Commulative law holds for Multification:
Example:
1. 32 x (- 4) = – 128 And (- 4) × 32 = – 128
∴ 32 x (- 4) = (- 4) × 32
2. (- 20) x 5 = – 100 and 5 x (- 20) = – 100
∴ (-20) × 5 = 5 × (-20) = – 100 ‘
∴(- 20) × 5 = 5 × (- 20)
2. Commutative law does not hold for Division.
Example:
1. 32 ÷ (- 4) = – 8 and (- 4)÷ 32 = \(\frac{1}{8}\)
∴ 32 ÷ (- 4) ≠ (- 4) ÷ 32
2. (- 20) ÷ 5 = – 4 & 5÷ (- 20) = – \(\frac{1}{4}\)
∴ (- 20) ÷-5 ≠ 5 (- 20)
Question 8. Let us take 2 examples to show that the commutative law holds in case of multiplication but does not always hold for the division of integers.
Solution:
1. Distribution law holds for Multiplication
1. 40 x {(- 8) + 4} = 40 x (- 4) = – 160
And 40 x (- 8) + 40 x 4 = – 320 + 160 = – 160
∴ 40 x {(- 8) + 4} = 40 x (- 8) + 40 x 4
2. 25 x (7 + 3) = 25×10 =250
And 25 x 7+ 25 x 3 = 175 + 75 = 250
∴ 25 x (7 + 3) = 25 x 7 + 25 x 3
2. Distribution law does not hold for Division:
1. For left distribution:
40 ÷ {(-8) + 4} = 40 ÷ (-8) + 40 – 4 = -5 + 10 = 5
& 40 ÷ {(- 8) + 4} = 40 + (- 4) = – 1 0
∴ 40 ÷ {(-8) + 4} * 40 -h (- 8) + 40 -r 4
2. For Right distribution.
{(- 8) + 4} 40 = – 4 ÷ 40 = – \(\frac{1}{10}\)
And {(-8) + 4} ÷ 40= \(\frac{-8}{40}+\frac{4}{40}=\frac{-1}{5}+\frac{1}{10}=\frac{-2+1}{10}=-\frac{1}{10}\)
Question 9. Let us find the values of the following
1. (- 125) ÷ 5
Solution:
(- 125) ÷ 5 = – 25
2. (-144) ÷6
Solution:
(-144) ÷6 = – 24
3. (- 49)÷ 7
Solution:
(- 49)÷ 7 = – 7
4. 225 ÷ (-3)
Solution:
225 ÷ (-3) = – 75
5. 169 ÷ (- 13)
Solution:
169 ÷ (- 13)= -13
6.100 ÷ (-5)
Solution:
100 ÷ (-5)= – 20
7. (-81) ÷ (-9)
Solution:
(-81) ÷ (-9) = 9
8. (- 150) ÷ (-5)
Solution:
(- 150) ÷ (-5) = (-81) + (-9)= 30
9. (-121) ÷ (-11)
Solution:
(-121) ÷ (-11)= 11
10.(- 275) ÷ (-25)
Solution:
(- 275) ÷ (-25) = 11