Class 7 Math Solution WBBSE Arithmetic Chapter 2 Ratio Exercise 2 Solved Problems
Ratio: A ratio is a method to compare two quantities of the same kind having same unit, obtained by dividing the first quantity by the second quantity.
⇒ Hence, the ratio is an abstract number, it has no units.
⇒ The ratio of a to b is written as a: b and is read as ‘a is to b’.
Terms of the ratio:
⇒ The two number which forms the ratio are called the “Terms of the ratio”.
Read and Learn More WBBSE Solutions for Class 7 Maths
⇒ The first term of the ratio is called ‘Antecedent’ and the second one is called the ‘Consequent”.
⇒ In the ratio 37, 3 is called the antecedent of the ratio, whereas 7 is called ‘Consequent’.
⇒ The ratio can be expressed in fractional form. The antecedent becomes the numerator and the consequent becomes the denominator of the fraction.
The ratio are mainly of two types:
1. Simple ratio
2. Mixed or Compound ratio
1. Simple ratio: The ratio between two quantities of the same kind is known as the simple ratio.
Example: 34, 8: 12.
2. Mixed or Compound ratio: The ratio whose antecedent is the product of the antecedents of two or more simple ratios and whose consequent is the product of the consequents of those ratios is termed as a mixed or compound ratio.
Example: The compound ratio of 2: 3, 5: 4, and 6: 8 is (2 x 5 x 6): (3 x 4 x 8) = 60: 96 = 5:8 [dividing each term by 12]
The simple ratio are of three types:
1. Ratio of greater equality (or Major Ratio): In this type of ratio, the antecedent is greater than the consequent.
Example: 5: 3.
2. Ratio of lesser inequality (or Minor Ratio): In this type of ratio, the antecedent is less than the consequent.
Example: 3: 7.
3. Ratio of Equality (or Equal Ratio): In this type of ratio, the antecedent is exactly equal to the consequent.
Example: 4: 4 or 1: 1.
Inverse Ratio: Of two ratios, if the antecedent and consequent of one are respectively the consequent and antecedent of the other, they are said to be inverse ratio or reciprocal to one another.
Example: the inverse ratio of 4:5 is 5: 4
The reciprocal fraction of \(\frac{7}{9} \text { is } \frac{9}{7}\)
Proportional part: To divide a given quantity into proportional parts is to divide it into parts that will be proportional to certain numbers.
Class 7 Math Solution WBBSE
Example: suppose divide ₹ 640 among A, B, and C in such a way that the money each gets will be in a ratio of 5: 3: 2. Find, how much money each of them gets.
Given
suppose divide ₹ 640 among A, B, and C in such a way that the money each gets will be in a ratio of 5: 3: 2.
A’s money B’s money: C’s money = 5:3:2
∴ Proportional part of A’s money = \(=\frac{5}{5+3+2}=\frac{5}{10}\)
⇒ Proportional part of B’s money = \(=\frac{3}{5+3+2}=\frac{3}{10}\)
⇒ Proportional part of C’s money=\(=\frac{2}{5+3+2}=\frac{2}{10}\)
⇒ Total money= ₹640
∴ A gets = ₹ \(\left(640 \times \frac{5}{10}\right)\) = ₹ 320
B gets = ₹ \(\left(640 \times \frac{3}{10}\right)\) = ₹ 192
C gets = ₹ \(\left(640 \times \frac{2}{10}\right)\) = ₹128
Question 1: The ratio of the ages of Samir and Aloke is 2: 3. If the age of Aloke is 12 yrs, then find the age of Samir.
Solution:
Given
The ratio of the ages of Samir and Aloke is 2: 3. If the age of Aloke is 12 yrs
\(\frac{\text { Age of Samir }}{\text { Age of Aloke }}=\frac{2}{3}\) \(\frac{\text { Age of Samir }}{12 \mathrm{yrs}}=\frac{2}{3}\)
∴ Age of Samir =
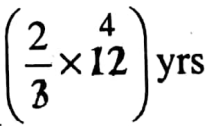
= 8 yrs.
The age of Samir = 8 yrs.
Wbbse Class 7 Maths Solutions
Question 2. The ratio of two numbers is 3: 4 and their H. C. F. is 15. Find the numbers and their L. C. M.
Solution:
Given
⇒ The ratio of two number is 3: 4.
⇒ Let the numbers are 3x and 4x [where x is common multiple and x > 0]
⇒ The H. C. F. of 3x and 4x is x and L. C. M. is (3 x 4 x x) or 12x.
⇒ According to question, x = 15
∴ The numbers are 3 x 15 or 45 and 4 x 15 or 60
⇒ Their LCM is 12 x 15 = 180.
Class 7 Math Solution WBBSE
Question 3. Reduce the following ratios into their lowest form and find their inverse ratios.
1. 225: 150
2. 20 ab: 25 ab [a ≠ 0, b ≠ 0]
Solution :
1. 225: 150
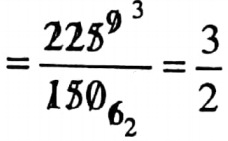
= 3 : 2
The inverse ratio of 3: 2 is 2: 3.
2. 20 ab: 25 ab
= 4 5 [dividing each term by 5ab]
⇒ The inverse ratio of 4 5 is 5:4
Wbbse Class 7 Maths Solutions
Question 4: Reduce the following into the ratio of the whole number and find their inverse ratio.
1. \(\frac{3}{8}: \frac{5}{16}\)
2. 0-125: 2.5
Solution: \(\frac{3}{8}: \frac{5}{16}\)
[L.C.M of 8 and 16 is 16]
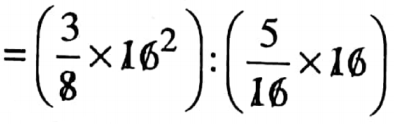
[Multiplying both terms by 16]
The inverse ratio of 6: 5 is 5: 6.
2. 0.125: 2.5
= \(\frac{0 \cdot 125}{2 \cdot 5}\)
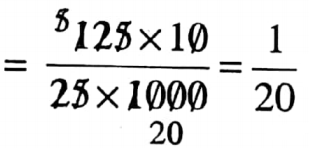
= 1:20
The inverse ratio of 1: 20 is 20: 1.
Class 7 Math Solution WBBSE
Question 5. Find the mixed ratio of the following ratios and identify the mixed ratio and find if these are ratios of greater or lesser inequality or ratio of equality.
1. 2 : 3, 4 : 5, and 6: 8
2. \(2 \frac{1}{3}: 3 \frac{1}{2}, 4 \frac{1}{2}: 5 \frac{2}{3} \text { and } 6: 1 \frac{1}{2}\)
3. 5:6, 3:2 and 4:5
Solution:
1. The mixed ratio of 2: 3, 4: 5, and 6: 8 is (2 x 4 x 6): (3 x 5 x 8) =48:120=
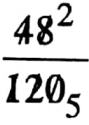
=2:5 [ratio of lesser in equality]
2. \(2 \frac{1}{3}: 3 \frac{1}{2}=\frac{7}{3}: \frac{7}{2}\)
\(4 \frac{1}{2}: 5 \frac{2}{3}=\frac{9}{2}: \frac{17}{2}\)\(6: 1 \frac{1}{2}=6: \frac{3}{2}\)
The mixed ratio of \(\frac{7}{3}: \frac{7}{2}, \frac{9}{2}: \frac{17}{2} \text { and } 6: \frac{3}{2}\) is
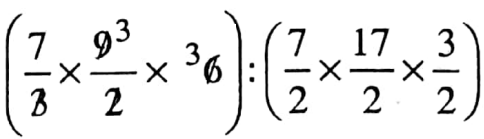
= 63 : \(\frac{357}{8}\)
= 36 x 8 : ![]() [Multiplying each term by 8]
[Multiplying each term by 8]
= 504:357
= 168:119
[ratio of greater inequality]
3. The mixed ratio of 5: 6, 3: 2, and 4: 5 is (5 x 3 x 4): (6 x 2 x 5)
= 60: 60
= 1:1 [ratio of equality]
Wbbse Class 7 Maths Solutions
Question 6: If A B = 2: 3 and B C 4 5. then find A: B: C.
Solution:
Given
A: B = 2:3= (2 x 4) : (3 x 4) = 8: 12
B: C 4:5 (4 x 3):(5 x 3) = 12 15
∴ A B C = 8: 12: 15
Question 7: If A: B=3: 4, B: C = 5:6, and C: D = 7: 8. then find
1. A: D and 2. A: B: C: D
Solution:
Given
A: B=3: 4, B: C = 5:6, and C: D = 7: 8
1.
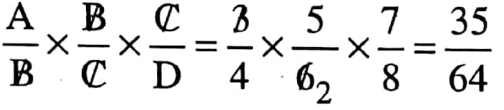
⇒ A:D= 35: 64
2. A:B = 3: 4 = (3 x 5): (4 x 5) = 15: 20
B:C = 5:6 (5 x 4): (6 x 4) = 20:24
A:B:C = 15 20 24
= (15 x 7):(20 x 7): (24 x 7)
= 105:140:168
Again, C:D = 7:8 = (7 x 24) (8 x 24)
= 168: 192
A:B: C:D = 105: 140: 168: 192
Wbbse Class 7 Maths Solutions
Question 8: The ratio between the speeds of two trains is 5: 6. If the first train runs 200 km in 5 hours find the speed of the second train.
Solution:
Given
The ratio between the speeds of two trains is 5: 6. If the first train runs 200 km in 5 hours
The first train in 5 hours runs 200 km
The first train in 1-hour runs \(\frac{200}{5}\) km = 40 km
∴ The speed of the 1st train is 40 km/hr
Let the speed of the second train is x km/hr.
According to question, 40: x = 5: 6
⇒ \(\frac{40}{x}=\frac{5}{6}\)
⇒ 5x = 40 x 6
⇒ 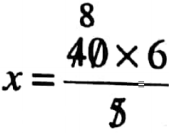
= 48
∴ The speed of the 2nd train is 48 km/hr.
Question 9: The ratio of the costs of two cars is 2 : 3 and the cost of the second car is 3,00,000. Find the cost of the first car. If the cost of the first car was 50,000 more, then find the ratio of their costs.
Solution:
Given
The ratio of the costs of two cars is 2 : 3 and the cost of the second car is 3,00,000. Find the cost of the first car. If the cost of the first car was 50,000 more
Let the cost of 1st car is ₹ x
According to question, x: 3,00,000 = 2:3
⇒ \(\)
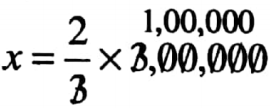
⇒ x= 2,00,000
∴ The cost of the first car is 2,00,000
If the cost of 1st car was 50,000 more, then the ratio of their cost is (2,00,000+ 50,000): 3,00,000
= 2,50,000 3,00,000
= 5:6
The ratio of their costs = 5:6
Question 10. Out of 100 sums, Arpita got 70 sums correct. Out of 80 of those sums, Kabita got 60 sums correct. Express them in ratio to find, who got more sums correct.
Solution:
Given
Out of 100 sums, Arpita got 70 sums correct. Out of 80 of those sums, Kabita got 60 sums correct.
Of Arpita the ratio of correct sums and the total sum is
70:100 = 7:10 = 7 x 2 : 10 x 2
= 14: 20
Of Kabita, the ratio of correct sums of the total sum is 60: 80 3:4 = 3 x 5:4×5 = 15:20
As 15 > 14,
∴ \(\frac{15}{20}>\frac{14}{20}\)
i.e 15:20:14:20
So Kabita got more sums correct.
Wbbse Class 7 Maths Solutions
Question 11: In a particular type of steel, the ratio of iron and carbon is 47: 3. Calculate to find in 300 kg of such steel how much iron is there.
Solution:
Given
In a particular type of steel, the ratio of iron and carbon is 47: 3.
The proportional parts of iron is
\(\frac{47}{47+3}=\frac{47}{50}\)The proportional parts of carbon is
\(\frac{3}{47+3}=\frac{3}{50}\)The quantity of steel in 300 kg of such steel is
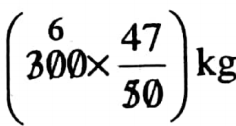
and the quantity of carbon is
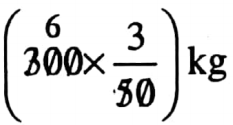
= 18 kg
The quantity of steel in 300 kg of such steel is 18 kg.
Question 12: In a certain year, Vivekananda Youth Library received a Govt. grant of 74,350 and collected a subscription of 4350. Also, they got 1300 by selling old paper etc. If the entire money is spent on buying new books, for binding of old books, and paying salaries to employees in the ratio of 15: 3:2. Calculate for how much money new books were bought.
Solution:
Given
In a certain year, Vivekananda Youth Library received a Govt. grant of 74,350 and collected a subscription of 4350. Also, they got 1300 by selling old paper etc. If the entire money is spent on buying new books, for binding of old books, and paying salaries to employees in the ratio of 15: 3:2.
Total income is ₹(74,350 + 4350+ 1300) = ₹80,000.
The entire money is spent of buying new books, for binding of old books, and paying salaries to employees in the ratio of 15:3:2.
Proportional parts of money on buying new books is \(\frac{15}{15+3+2}=\frac{15}{20}\)
The cost for buying new books is
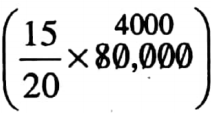
= ₹ 60,000
The cost for buying new books = ₹ 60,000
Wbbse Class 7 Maths Solutions
Question 13. The ratio between the average temperatures of Kolkata and Mumbai is 8: 7 and that between Kolkata and Delhi is 4: 5. Find the ratio of the average temperature of Mumbai and Delhi.
Solution:
Given
The ratio between the average temperatures of Kolkata and Mumbai is 8: 7 and that between Kolkata and Delhi is 4: 5.
\(\frac{\text { Temperature of Kolkata }}{\text { Temperature of Mumbai }}=\frac{8}{7}\)
⇒ \(\frac{\text { Temperature of Mumbai }}{\text { Temperature of Kolkata }}=\frac{7}{8}\)
again, ⇒ \(\frac{\text { Temperature of Kolkata }}{\text { Temperature of Delhi }}=\frac{4}{5}\)
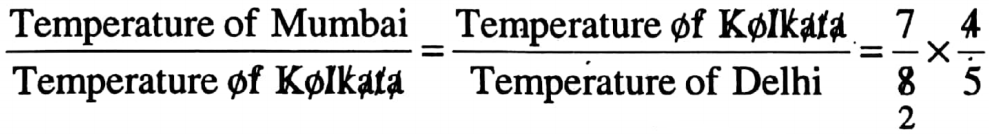
∴ Temperature of Mumbai = Temperature of Delhi = 7: 10
Class 7 Math Solution WBBSE
Question 14. Divide 23,001 between A and B in the \(\frac{2}{3}: \frac{3}{4}\)
Solution:
\(\frac{2}{3}: \frac{3}{4}:\left(\frac{2}{3} \times 12\right):\left(\frac{3}{4} \times 12\right)=8: 9\)Proportional part of A’s money = \(\frac{8}{8+9}=\frac{8}{17}\)
Proportional part of B’s money = \(\frac{9}{8+9}=\frac{9}{17}\)
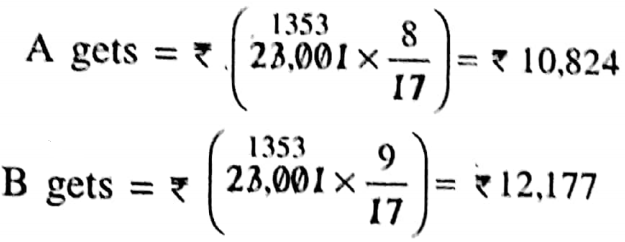
Class VII Math Solution WBBSE Ratio
Ratio Exercise 2
Question 1.1 kg of rice costs Rs. 40 and 1 kg of pulse costs Rs. 100. Let’s find the ratio of the prices of rice and pulse.
Solution:
Given
1 kg of rice costs Rs. 40 and 1 kg of pulse costs Rs. 100.
⇒ \(\frac{\text { Price of } 1 \mathrm{~kg} \text { rice }}{\text { Price of } 1 \mathrm{~kg} \text { pulse }}=\frac{\text { Rs. } 40}{\mathrm{RS} .100}\)
⇒ \(\frac{40}{100}\)
⇒ \(\frac{2}{5}\)
2:5
∴ The ratio of the prices of rice and pulse =2:5
Question 2. ∠BAC: ∠ABC: ∠ACB = What?
Solution :
∠BAC : ∠ABC: ∠ACB = 60= : 50° : 703 =6:5:7
Question 3. The price of a pencil is Rs. 3 and the cost of a toffee is 50 paise. Let’s write the ratio of the prices of a pencil and a toffee.
Solution :
Given
The price of a pencil = Rs. 3 = 300 p.
The price of a toffee = 50p
⇒ \(\frac{\text { The price of a pencil }}{\text { The price of a toffee }}=\frac{300 p}{50 p}\)
⇒ \(\frac{6}{1}\)
6:1
∴ The ratio of the price of a pencil and a’toffeee is 6 : 1.
Question 4. Let’s find the ratio of the values of a 50 p coin, a rupee coin, and a two rupee coin.
Solution :
The value of a 50 p. coin; a rupee coin ; a two rupee coin
= 50 : 100 : 200 = 1 : 2 : 4
Class VII Math Solution WBBSE
Question 5. Lima’s age is 12 yrs 6 m, Ratul’s age is 12 yrs 4 m and Noorjahan’s age is 12 yrs. Let’s write the ratio of their ages.
Solution :
Given
Lima’s age = 12 yrs 6 m = (12 × 12 + 6) m = 150 m
Rahul’s age = 12 yrs 4 m = (12 × 12 + 4) m = 148 m.
Noorjahan’s age = 12 yrs = (12 × 12) m = 144 m.
∴ The ratio of their ages
= 150 m : 148 m : 144 m = 150 : 148 : 144 = 75 : 74 : 72
Question 6. Let’s write the ratio of the angles of a right-angled isosceles triangle.
Solution:
The angles of right angles isosceles triangle are 90°, 45° & 45°
∴ The ratio of the angles = 90° : 45° : 45° =2:1:1
Question 7. Let’s write the ratio of the angles of an equilateral triangle.
Solution :
Each angle of an equilateral triangle = 60°
∴ The ratio of the 3 angles of an equilateral triangle
= 60° : 60° : 60° =1:1:1
Question 8. The ratio of the ages of Pulakbabu and Manikbabu is 7: 9. If the age of Manikbabu is 72 years, let’s find the age of Pulakbabu.
Solution:
Given
The ratio of the ages of Pulakbabu and Manikbabu is 7: 9. If the age of Manikbabu is 72 years
⇒ \(\frac{\text { Age of Pulakbabu }}{\text { Age of Manikbabu }}=\frac{7}{9}\)
Or , \(\frac{\text { Age of Pulakbabu }}{72 \mathrm{yrs}}=\frac{7}{9}\)
Or, 9 Age of Pulkbabu= 7 × 72 yars
∴ Age of Pulakbabu = \(\frac{7 \times 72}{9}\) = 56 yrs
Class VII Math Solution WBBSE
Question 9. The ratio of the prices of two books is 2 : 5. If the price of the first book is Rs. 32.20, let’s find the price of the other book.
Solution :
Given
The ratio of the prices of two books is 2 : 5. If the price of the first book is Rs. 32.20
⇒ \(\frac{\text { The price of the } 1 \text { st book }}{\text { The price of the } 2 \text { nd book }}=\frac{2}{5}\)
Or , \(\frac{\text { Rs. } 32.20}{\text { The price of the } 2 \text { nd book }}=\frac{2}{5}\)
Or, 2 x The price of the 2nd book = 5 × Rs. 32.20
The price of the 2nd book = \(\frac{5 \times \text { Rs. } 32.20}{2}\)
=5 × Rs. 16.10 = Rs. 80.50
The price of the 2nd book = Rs. 80.50
Question 10. The ratio of the circumference and diameter of a circle is 22: 7. If the length of the diameter of the circle is 2m Idem., let’s calculate its circumference.
Solution:
Given
The ratio of the circumference and diameter of a circle is 22: 7. If the length of the diameter of the circle is 2m Idem
⇒ \(\frac{\text { Circumference }}{\text { Diameter }}=\frac{22}{7}\)
Or, \(\frac{\text { Circumference }}{2 \mathrm{~m} \mathrm{1dcm}}=\frac{22}{7}\)
Or, 7 x circumference = 22 × 2m 1 dcm
Circumference= \(\frac{22 \times 21 \mathrm{dcm}}{7}\)
= 66 dcm
= 6m 6dcm.
Circumference = 6m 6dcm.
Question 11. From our class seven, out of 150 students, 90 students and from 140 students of class six, 80 students participated in a sit-in-draw competition. Let’s express in ratio to find which of the two class has a greater participation.
Solution :
Given
From our class seven, out of 150 students, 90 students and from 140 students of class six, 80 students participated in a sit-in-draw competition.
In Class 7:
The ratio of participent = \(\frac{90}{150}=\frac{3}{5}\)
= \(\frac{3 \times 7}{5 \times 7}=\frac{21}{35}\)
In Class 6:
The ratio of participant
= \(\frac{80}{140}=\frac{4}{7}\)
= \(\frac{4 \times 5}{7 \times 5}=\frac{20}{35}\)
∴ Class 7 has a greater participation.
Question 12. The ratio of two numbers is 5: 7 and their H.C.F is 13. Let us find the numbers.
Solution:
Given
The ratio of two numbers is 5: 7 and their H.C.F is 13.
Let the numbers be 5x & 7x
Their H C F x = 13 (given)
1st number is 5x = 5 × 13 = 65
The 2nd number is 7x = 7 × 13 = 91
⇒ 65 and 91.
Class VII Math Solution WBBSE Ratio Exercise 2.1
Question 1. I shall prepare tea by mixing liqueur tea and milk in the same ratio. Let’s find how many cups of liqueur tea and how many cups of milk will be needed for preparing tea.

1. 24 Cups of tea, let’s find the ratio of liqueur tea and milk.
Solution:
In 24 Cups of tea, the ratio of liqueur tea and milk = 1 6 cups: 8 cups=2:1.
2. 15 Cups of tea, let’s find how many cups of milk are required.
Solution:
In 15 cups of tea, milk requires 5 cups.
Question 2. In the table given below, let’s fill up the blank squares
Let’s find the mixed ratio of the following :
1. 5 :3 , 8 : 12 & 7: 3
Solution:
A mixed ratio of 5: 9, 8: 12 & 7 : 3 is
⇒ \(\frac{5}{9} \times \frac{8}{12} \times \frac{7}{3}=\frac{5 \times 2 \times 7}{9 \times 3 \times 3}\)
⇒ \(\frac{70}{81}\)
70: 81
5 :3 , 8 : 12 & 7: 3 = 70: 81
2. 1.2: 5, 3.5: 7 and 6: 4
Solution :
Mixed ratio of 1 .2 : 5, 3.5 : 7 & 6 : 4 is
⇒ \(\frac{12}{10 \times 5} \times \frac{35}{10 \times 7} \times \frac{6}{4}\)
⇒ \(\frac{9}{50}\)
= 9:50
1.2: 5, 3.5: 7 and 6: 4 = 9:50
Class VII Math Solution WBBSE
3. \(\frac{3}{5}: 2, \frac{5}{6}: 3\) and 4:5
Solution :
Mixed ratio of\(\frac{3}{5}: 2, \frac{5}{6}: 3\) and 4:5
⇒ \(\frac{3}{5} \times \frac{1}{2} \times \frac{5}{6} \times \frac{1}{3} \times \frac{4}{5}\)
⇒ \(\frac{1}{15}\)
= 1:15
\(\frac{3}{5}: 2, \frac{5}{6}: 3\) and 4:5 = 1:15
Class VII Math Solution WBBSE Ratio Exercise 2.2
Question 1. Reduce the following ratios to their lowest form and let’s find their inverse ratio.
1. 12: 15
Solution :
12 : 15 = 4 : 5
Its inverse ratio = 5:4
2. 36: 54
Solutions :
36 : 54 = 2 : 3
Its inverse ratio = 3:2
3. 75: 120
Solution :
75 : 120 = 5 : 8
Its inverse ratio = 8:5
4. 169: 221
Solution :
169 : 221 = 13 : 17
Its inverse ratio
= 17: 13
5. 9xy : 12xy
Solution :
9xy : 12xy = 3 : 4
Its inverse ratio = 4:3
6. 429: 663
Solution :
429 : 663 = 11 : 17
Its inverse ratio = 17:11
7. 3b: 12c
Solution :
3b : 12c = b : 4c
Its inverse ratio = 4c : b
8. 25xyz : 625xyz (Where a, b, x, y, z are not zero).
Solution :
25xyz : 625xyz =1 : 25
Its inverse ratio = 25 : 1
Question 2. Reduce the following into the ratio of whole numbers and let’s find their inverse ratio.
1. 2.5: 12.5
Solution : 2.5 : 12.5 = 1 : 5
Its inverse ratio = 5:1
2. \(\frac{5}{8}: \frac{7}{16}\)
⇒ \(\frac{5}{8}: \frac{7}{16}=\left(\frac{5}{8} x^{16}\right):\left(\frac{7}{16} x^{16}\right)\)
10: 7 and its inverse
Ratio= 7: 10
3. 0.7: 0.49
Solution:
0.70 : 0.49 = 10 : 7 = & its inverse ratio = 7:10
4. \(\frac{2}{5}: \frac{3}{4}\)
Solution:
⇒ \(\frac{2}{5}: \frac{3}{4}=\left(\frac{2}{5} x^{20}\right):\left(\frac{3}{4} x^{20}\right)\)
= 8: 15
Its inverse ratio = 15: 8
5. \(22: 4 \frac{5}{7}\)
Solution :
⇒ \(22: \frac{32}{7}=2: \frac{3}{7}\)
= 14 : 3 & its inverse ratio
= 3:14
\(22: 4 \frac{5}{7}\) = 3:14
6. \(\frac{7}{15}: \frac{3}{20}\)
Solution :
⇒ \(\frac{7}{15}: \frac{3}{20}\)
⇒ \(\left(\frac{7}{15} x^{60}\right):\left(\frac{3}{20} x^{60}\right)\)
= 28 : 9 & its inverse
Ratio = 9: 28
Class VII Math Solution WBBSE
7. \(1 \frac{2}{5}: \frac{7}{10}\)
Solution : \(1 \frac{2}{5}: \frac{7}{10}=\left(\frac{7}{5} x^{10}\right):\left(\frac{7}{10} x^{10}\right)\)
Inverse ratio = 1: 2
8. 4. 4: 5.61
Solution : 4. 4 : 5.61 = 4.40 : 5.61 = 440 : 561
= (440 ÷11): (561÷11) = 40: 51 & its inverse ratio
Question 3. Let’s find the mixed ratio of the following ratios and let’s identify the mixed ratio and find if these are ratios of greater or lesser inequality or ratio of equality.
1. 8: 6, 3: 6 and 26: 13
Solution :
A mixed ratio of 8: 6, 3: 6 & 26: 13 is
⇒ \(\frac{8}{6} \times \frac{3}{6} \times \frac{26}{13}=4: 3\)
The mixed ratio is of greater inequality.
2. \(\frac{7}{5} \times \frac{1}{3} \times \frac{5}{7} \times \frac{16}{17} \times \frac{3}{16}\)
Solution :
Mixed ratio of \(\frac{7}{5}: 3, \frac{5}{7}: 1 \frac{1}{16} \& 3: 16\) is
⇒ \(\frac{7}{5} \times \frac{1}{3} \times \frac{5}{7} \times \frac{16}{17} \times \frac{3}{16}\)
⇒ \(\frac{1}{17}\)
The mixed ratio is of lesser inequality.
= 1:17
The mixed ratio is of lesser inequality.
3. 8: 5, 7: 12 and 22: 13,
Solution :
Mixed ratio of 8: 5, 7: 12 and 22: 13 is
⇒ \(\frac{8}{5} \times \frac{7}{12} \times \frac{22}{13}\)
= \(\frac{308}{195}\)
= 308:195
The mixed ratio is of greater inequality.
4. \(\frac{2}{3}: 5, \frac{7}{8}:\)
Solution :
Mixed ratio of \(\frac{2}{3}: 5, \frac{7}{8}:\) is
⇒ \(\frac{2}{3} \times \frac{1}{5} \times \frac{7}{8} \times \frac{1}{2}=\frac{7}{120}\)
= 7:20
Question 4. Out of 100 sums, Rita got 60 sums correct. Out of 80 of those sums, Binoy got 50 sums correct. Let’s express them in ratio to find, who got more sums correct.
Solution:
Given
Out of 100 sums, Rita got 60 sums correct.
∴ Rita’s ratio = \(\frac{60}{100}=\frac{3}{5}\) = 3:5
Out of 80 sums Binoy got 50 sums correct
∴ Bjnoy’s ratio = \(\frac{50}{80}=\frac{5}{8}\)
= 5: 8
Now , \(\frac{3}{5}=\frac{3 \times 8}{5 \times 8}\)
= \(\frac{24}{40}\)
∴ Binoy got more sums correct.
Question 5. In this year’s Madhymik examination out of 150 examinees of our school, 100 examinees passed with a grade – A. In another nearby school out of 100 examinees, 80 examinees passed with a grade – Of a. Let’s find which school has got a better result getting a grade – Of a, in this year’s Madhyamik examination.
Solution :
Given
In this year’s Madhymik examination out of 150 examinees of our school, 100 examinees passed with a grade – A. In another nearby school out of 100 examinees, 80 examinees passed with a grade – Of a
In our school, out of 150 examinees, 100 examinees got
∴ Ratio of getting grade A = \(\frac{100}{150}\)
= \(\frac{2}{3}\)
= 2:3
Percentage of getting grade A
= \(\frac{2}{3} \times 100 \%\)
= \(\frac{200}{3} \%\)
= \(66 \frac{2}{3} \%\)
In another school out of 100 examinees, 80 examinees got a grade A.
Ratio of getting grade A = \(\frac{80}{100}\)
= \(\frac{4}{5}\)
= 4: 5 and the percentage of getting grade A = \(\frac{4}{5}\) 100%
= 80 %
∴ The neighbouring school got a better result getting a grade of A.
Question 6. The ratio of the costs of two houses is 4 : 3 and the cost of the second house is Rs. 4,20,000. Let’s find the cost of the first house. If the cost of the first house was Rs. 70,000 more, then let’s find the ratio of their costs.
Solution:
Given
The ratio of the costs of two houses is 4 : 3 and the cost of the second house is Rs. 4,20,000. Let’s find the cost of the first house. If the cost of the first house was Rs. 70,000 more,
⇒ \(\frac{\text { Cost of 1st house }}{\text { Cost of 2nd house }}=\frac{4}{3}\)
⇒ \(\frac{\text { Cost of 1st house }}{\text { Rs. } 4,20,000}=\frac{4}{3}\)
∴ 3 × cost of 1st house = 4 × Rs. 4,20,000
Cost of 2nd house = \(\frac{4 \times 4,20,000}{3}\)
= Rs. 4 x 1 ,40,000 = Rs, 5,60,000
Question 7. From a bamboo, a piece of bamboo is cut off. It is found that the ratio of the two pieces is 3: 1. From the table below, let’s find the possible lengths of the two pieces and the length of the bamboo.
Solution:

∴ Ratio of the length of the bamboos = 40 dcm: 60 dcm = 2:3 (Ans.)
Class 7 Math Solution WBBSE Ratio Exercise 2.3
Question 1. Last year, the ratio of literate and illiterate people of Rashkundu Village was 4: 1. If the population of the village is 6550, let’s find the numbers of literate and illiterate people
Solution :
Given
⇒ Last year, the ratio of literate and illiterate people of Rashkundu Village was 4: 1. If the population of the village is 6550
⇒ Ratio of literate & illiterate people = 4:1
⇒ Total population of the village = 6550
∴ Proportional part of literate people = \(\frac{4}{4+1}=\frac{4}{5}\)
⇒ And proportional part of illiterate people = \(\frac{4}{4+1}=\frac{4}{5}\)
∴ No. of literate people = \(\frac{4}{5} \times 6550\) = 4 × 1310
= 5240
⇒ No. of illiterate people = \(\frac{4}{5} \times 6550\)= 1 × 1310 = 1310
Question 2. If Rs. 640 is divided between Bishu and Aparna in the ratio of 5 : 3, let’s find how much each would get.
Solution :
Given
⇒ Rs. 640 is divided between Bishu and Aparna in the ratio of 5 : 3
⇒ The ratio of Bishu’s amount = 5:3
∴ Proportional part of Bishu’s amount = \(\frac{5}{5+3}=\frac{5}{8}\)
⇒ And Proportional part of Aparna’s amount = \(\frac{3}{5+3}=\frac{3}{8}\)
⇒ Total amount = Rs. 640
∴ Bishu’s share = Rs. \(640 \times \frac{5}{8}\) = Rs. 80 × 5= Rs. 400
⇒ Aparna’s share = Rs. \(640 \times \frac{5}{8}\) = Rs. 80 × 3 = Rs. 240
Question 3. In a particular type of steel, the ratio of iron and carbon is 49: 1. Let’s calculate to find, in 250 quintals of such steel how much iron is there.
Solution :
Given
⇒ In a particular type of steel, the ratio of iron and carbon is 49: 1.
⇒ Ratio of Iron & Carbon = 49: 1
⇒ And Proportional part of Iron = \(\frac{49}{49+1}=\frac{49}{50}\)
⇒ And proportional part of Carbon =\(\frac{1}{49+1}=\frac{1}{50}\)
⇒ The total quantity of steel = 250 quintals
∴ Quality Of Iron = \(\frac{49}{50} \times 250\) quintal
49 5 quintal = 245 quintal
Question 4. Out of 143 girls in a school, the ratio of the number of girls who can only sing and those who can dance is 9: 2. If 3 more girls were found to sing, then let’s find the new ratio of girls who can sing and those who can dance.
Solution :
Given
⇒ Out of 143 girls in a school, the ratio of the number of girls who can only sing and those who can dance is 9: 2. If 3 more girls were found to sing
⇒ Ratio of number of girls who can sing & number of. girls
⇒ Who can dance = 9:2
∴ Proportional part of girls who can sing = \(\frac{9}{9+2}=\frac{9}{11}\)
⇒ And proportional part of girls who can dance = \(\frac{2}{9+2}=\frac{2}{11}\)
⇒ Total number of girls = 143
∴ No. of girls who can sing = \(\frac{9}{11} \times 143\) = 9×13 = 117
⇒ No. of girls who can dance = \(\frac{2}{11} \times 143\)
⇒ If 3 more girls are found to sing, the total number of girls who can sing
= 117 + 3 =120.
= 2 × 13 = 26
∴ A new ratio of girls who can sing and those who can dance
= 120 : 26 = 60 : 13.
Class 7 Math Solution WBBSE Question 5. In 240 ml of Dettol-water, the ratio of the volumes of water and Dettol is 1 : 3. If 60 ml of water is added to it, let’s find the ratio of the volume. water and Dettol in the new mixture.
Solution :
Given
⇒ In 240 ml of Dettol-water, the ratio of the volumes of water and Dettol is 1 : 3. If 60 ml of water is added to it,
⇒ Ratio of volume water and Dettol = 1:3
∴ Proportional volume of water = \(\frac{1}{1+3}=\frac{1}{4}\)
⇒ And proportional volume of Dettol = \(\frac{3}{1+3}=\frac{3}{4}\)
⇒ Total volume of Dettol water mixture = 240 ml.
∴ Volume of water in this mixture = \(\frac{1}{4} \times 240 \mathrm{ml}\) = 60 ml.
⇒ And Volume of Dettol in the mixture = \(\frac{3}{4} \times 240 \mathrm{ml}\) = 180 ml
Question 6. The monthly income of a man is Rs. 24,750. He pays house rent of Rs. 750 and the remaining money is spent on household expenses and the education of children in the ratio of 3:1. Let’s find how much money is spent on household expenses.
Solution :
Given
⇒ The monthly income of a man is Rs. 24,750. He pays house rent of Rs. 750 and the remaining money is spent on household expenses and the education of children in the ratio of 3:1.
⇒ Total monthly income = Rs. 24,750.
⇒ He pays for House rent = Rs. 750
⇒ Remaining money = Rs. 24000.
⇒ Now the ratio of expenses for household & educational experiences = 3:1
⇒ Proportional part of household expenses = \(\frac{3}{3+1}=\frac{3}{4}\)
⇒ And proportional part of educational expenses = \(\frac{1}{3+1}=\frac{1}{4}\)
∴ Expenses for household = \(\frac{3}{4}\) × Rs.2400
= 3 × Rs. 6,000 = Rs. 18,000.
Question 7. In a certain year, Vivekananda Youth Library received a Govt. grant of Rs. 74,350 and collected a subscription of Rs. 4,350. Also, they got Rs. 1,300 by selling old papers, etc. If the entire money is spent on buying new books, for binding old books and paying salaries to employees in the ratio of 15 : 3: 2. Now let’s calculate how much money new books were bought.
Solution :
Given
In a certain year, Vivekananda Youth Library received a Govt. grant of Rs. 74,350 and collected a subscription of Rs. 4,350. Also, they got Rs. 1,300 by selling old papers, etc. If the entire money is spent on buying new books, for binding old books and paying salaries to employees in the ratio of 15 : 3: 2.
Total income of Vivekananda Youth Library
= Rs (74350 + 4350 + 1300) = Rs. 80,000
Now, the ratio of expenses for buying newÿooks, for binding old books
And paying salary to employees = 15 : 3 : 2
∴ Proportional part for expenditure on buying new books
= \(\frac{15}{15+3+2}\frac{15}{20}=\frac{3}{4}\)
∴ Expenditure for buying new books
= Rs. 80,000 x \(\frac{3}{4}\)
= Rs. 20,000 × 3
= Rs. 60,000
Proportional part for expenditure on buying new books is Rs. 60,000
Class 7 Math Solution WBBSE Question 8. 1050 people have come for training at a training center. They were asked to sit in three big halls in the ratio of Let’s find how many people will sit in each room.
Solution :
Given
⇒ 1050 people have come for training at a training center.
⇒ Ratio of sitting in three big rooms = 11:3:3\(\frac{1}{2}\)
= 11:3: = 22: 6: 7
∴ Proportional part of sitting in the 1st room = \(\frac{22}{22+6+7}\) = \(\frac{22}{35}\)
⇒ Propotional part of sitting in the 2nd room = \(\frac{6}{22+6+7}\) = \(\frac{6}{35}\)
⇒ The proportional part of sitting in the 3rd room = \(\frac{7}{22+6+7}\) = \(\frac{7}{35}\)
Total number of people = 1050
∴ No. of people will sit in 1st room = \(\frac{22}{35} \times 1050\) = 66o
⇒ No. of people will sit in 2nd room =\(\frac{6}{35} \times 1050\) = 180
⇒ No. of people will sit in 3rd room = \(\frac{7}{35} \times 1050\) = 210
Question 9. Rs. 12,000 is divided among Madhu, Manas, Kuntal, and Indra 2, let’s calculate how much each will get.
Solution :
Given
⇒ Rs. 12,000 is divided among Madhu, Manas, Kuntal, and Indra 2,
⇒ Ratio of amount of Madhu, Manas, Kuntal & Indra = 2 : 3 : 4 : 2
⇒ Proportional part of Madhu’s money = \(\frac{2}{2+3+4+2}=\frac{2}{11}\)
⇒ Proportional part of Manas’s money = \(\frac{3}{2+3+4+2}=\frac{3}{11}\)
⇒ Proportional part of Kuntal’s money = \(\frac{4}{2+3+4+2}=\frac{4}{11}\)
⇒ Proportional part of Indra’s money = \(\frac{2}{2+3+4+2}=\frac{3}{11}\)
⇒ Total Amount = Rs. 12100
∴ Madhu will get = \(\frac{2}{11} \times \text { Rs. } 12100\) = 2 x 1100 = Rs. 2200
⇒ Manas will get = \(\frac{3}{11} \times \text { Rs. } 12100\) = 3 x 1100 = Rs. 3300
⇒ Kuntal will get = \(\frac{4}{11} \times \text { Rs. } 12100\) = 4 x 1100 = Rs. 4400
⇒ Indra will get = \(\frac{2}{11} \times \text { Rs. } 12100\) = 2 x 1100 = Rs. 2200
Question 10. The sum of the three angles of a triangle ABC is -180° The ratio of ∠BAC, ∠ABC, and ∠ACB is 3: 5: 10. If the value of ∠BAC is decreased by 10° ar|d value of an ∠ABC is increased by io°- Let’s calculate the new ratio of the three angles.
Solution :
Given
⇒ The sum of the three angles of a triangle ABC is -180° The ratio of ∠BAC, ∠ABC, and ∠ACB is 3: 5: 10. If the value of ∠BAC is decreased by 10° ar|d value of an ∠ABC is increased by 1o°
⇒ Ratio of the. 3 angles of a triangle = 3 : 5 : 10
⇒ Proportional part of the 1st angle ( ∠BAC) = \(\frac{3}{3+5+10}=\frac{3}{18}\)
⇒ Proportional part of the 2nd angle ( ∠ABC ) = \(\frac{5}{3+5+10}=\frac{5}{18}\)
⇒ And proportional part of the 3rd angle ( ∠ACB)=\(\frac{10}{3+5+10}=\frac{10}{18}\)
⇒ The sum of the three angles of a triangle = 180°
⇒ Measure of 1st angle ( ∠BAC ) = \(\frac{3}{8} \times 180^{\circ}\) = 3 ×10° = 30°
⇒ Measure of 2nd angle ( ∠ABC ) = \(\frac{5}{18} \times 180^{\circ}\)= 5 × 10° = 50°
⇒ Measure of 3rd angle ( ∠ACB ) = \(\frac{10}{18} \times 180^{\circ}\)= 10 × 10° = 100°
⇒ After decreasing – 10° , the value fo 1st angle ( ∠BAC ) = 30°-105 -20°
⇒ After increasing 10° > the value of 2nd angle ( ∠ABC ) = 50° +10° =60°
⇒ The new ratio of the three angel = 20° : 60° : 100° =2:6:10
= 1:3:5
Question 11. Let’s divide Rs. 9,000 among three friends in such a way that the second friend gets twice the amount the first friend gets. and the third friend gets half of the total sum of money the two friends have got. Let’s calculate how much amount of money each friend will get. [if the first friend gets Re.1, the second friend will get Rs.2, and the third friend will get Rs. \(\frac{1+2}{2}\)= Rs \(\frac{3}{2}\). The ratio of the amount of money that three friends get is = 1:2:1 = 2:4:3
Solution:
Let the 1st friend get Re. 1
⇒ 2nd friend gets = 2 x Re. 1 = Rs. 2
⇒ The 3rd friend gets = Rs. \(\frac{1+2}{2}\) = \(\frac{3}{2}\)
∴ The ratio of the amount of money that three friends get
= 1:2:\(\frac{3}{2}\) = 2:4:3
⇒ Total amount of money = Rs. 9,000
⇒ Proportional part of money of 1st friend =\(\frac{2}{2+4+3}=\frac{2}{9}\)
⇒ Proportional part of moeny of 2nd friend = \(\frac{4}{2+4+3}=\frac{4}{9}\)
⇒ Proportional part of money of 3rd friend = \(\frac{3}{2+4+3}=\frac{2}{9}\)
∴ 1 st friend will get = Rs. \(9000 \times \frac{2}{9}\) = Rs. 1000 × 2 = Rs. 2000
⇒ 2nd friend will get = Rs. \(9000 \times \frac{4}{9}\) = Rs. 1000 × 4 = Rs. 4000
⇒ 3rd friend will get =Rs. \(9000 \times \frac{3}{9}\) = Rs. 1000 × 3 = Rs. 3000.
Question 12. For constructing a road in our village, the ratio of the money spent for the last four,r years is 2: 4 : 3: 2. If the total money spent in those four years is Rs. 132 lac, then let’s find how much money was spent on the second year and total money spent on first and third year.
Solution :
⇒ The ratio of the amount of money spent for the last four year = 2:4:3:2
∴ Proportional amount of money spent on 1 st year = \(\frac{2}{2+4+3+2}=\frac{2}{11}\)
⇒ Proportional amount of money spent on 2nd year = \(\frac{4}{2+4+3+2}=\frac{4}{11}\)
⇒ Proportional amount of money spent on 3rd year = \(\frac{3}{2+4+3+2}=\frac{3}{11}\)
⇒ And the Proportional amount of money spent on 4th year = \(\frac{2}{2+4+3+2}=\frac{2}{11}\)
⇒ Total money spent in those four years = Rs. 132 lac.
⇒ Amount of money spent on the second year
= \(\frac{4}{11}\) × 132 lac = 4×12 lac = 48 lac.
⇒ Amount of money was spent on the third year
= \(\frac{2}{11}\) × Rs. 132 lac = 2 x 12 lac = 24 lac.
⇒ Amount of money spent on the first year
= \(\frac{3}{11}\) × Rs. 132 lac = 3 x 12 lac = 36 lac.
Total Amount of money spent on the 1st and 3rd year
= 24 lac + 36 lac = 60 lac.
Another was :
⇒ Let the amount of money spent on the 1st year = Rs. 2x lac.
⇒ Amount of money spent on the 2nd year = Rs. 4x lac.
⇒ Amount of money spent on the 3rd year = Rs. 3x lac.
⇒ Amount of money spent on the 4th year = Rs. 2x lac.
⇒ Total amount of money spent on four years = Rs. 132 lac.
2x + 4x + 3x + 2x = 132
11x = 132
x = \(\frac{132}{11}\)
x = 12
⇒ Amount of money spent on the 2nd year
= Rs. 4x lac = Rs 4 × 12 lac = Rs. 48 lac
⇒ Amount of money spent last year and 3rd year
Rs. (2x + 3x) = 5x = Rs. 5 × 12 lac = 60lac
Class 7 Math Solution WBBSE Question 13. During retirement, Binoybabu gets Rs. 1,96,150. He donated Rs. 20,000 to the school library and the remaining amount he divided among his wife, son, and daughter in the ratio of 5: 4: 4. Let’s find out how much money he gave each of them.
Solution :
Given
During retirement, Binoybabu gets Rs. 1,96,150. He donated Rs. 20,000 to the school library and the remaining amount he divided among his wife, son, and daughter in the ratio of 5: 4: 4.
⇒ The total amount of money Binoybabu gets = Rs. 1,96,150
⇒ He gives a donation for the school library = Rs. 20,000
⇒ Remaining among = Rs. 1,76,150
⇒ The ratio of the amount of money he divided among his wife, son daughter = \(\frac{5}{5+4+4}=\frac{5}{13}\)
⇒ Proportional amount of money for his wife = \(\frac{5}{5+4+4}=\frac{5}{13}\)
⇒ Proportional amount of money for his son = \(\frac{4}{5+4+4}=\frac{4}{13}\)
⇒ Proportional amount of money for his daughter = \(\frac{4}{5+4+4}=\frac{4}{13}\)
⇒ Amount of money he gave to his wife = \(\frac{15}{4}\) Rs. 176150
= Rs. 5 × 13550= Rs. 67750.
⇒ Amount of money the gave to his son = \(\frac{4}{13}\)
Rs. 4 ×13550 = Rs. 54200
⇒ Amount of money the gave to his daughter = \(\frac{4}{13}\) × Rs. 176150
= Rs. 54200
Question 14. Aminoor uncle cultivated brinjal and potato in a ratio of 4 : 3 is his 35 katha land. He made a profit of Rs. 150 per katha for brinjal and Rs. 125 per katha for potato. Let’s calculate the total amount of profit of Aminoor’s uncle from his cultivation of brinjal and potato in his total land.
Solution :
Given
⇒ Aminoor uncle cultivated brinjal and potato in a ratio of 4 : 3 is his 35 katha land. He made a profit of Rs. 150 per katha for brinjal and Rs. 125 per katha for potato.
⇒ Ratio of area land for cultivation brinjal and potato = 4:3
⇒ The total area of land of Aminoor uncle = 35 Katha
⇒ Area of land for cultivation of brinjal = \(\frac{4}{7}\) x Rs. 35 Katha
= 4 × 5 katha = 20 Katha.
⇒ Area of land for cultivation potato = (35 – 20) Katha = 15 Katha
⇒ Now profit for cultivation of brinjal = Rs. 150 per Katha& profit for cultivation potato = Rs. 125 per Katha
⇒ Profit for cultivation of brinjal in 20 Katha = Rs. 150 × 20 = Rs. 3000
⇒ Profit for cultivation of potato in 15 Katha = Rs. 125× 15 = Rs. 1875
⇒ The total amount of profit of Aminoor’s uncle for the cultivation of brinjal & potato
= Rs. 3000+ Rs. 1875
= Rs. 4875
⇒ Ratio of profit for cultivation of brinjal & potato
= Rs. 3000: Rs. 1875
= 200: 125 (dividing both by 15)
= 8:5 (dividing both by 2)
