WBBSE Solutions For Class 7 Maths Arithmetic Chapter 3 Proportion Exercise 3 Solved Problems

Class 7 Math Solution WBBSE Arithmetic Chapter 3 Proportion Exercise 3 Solved Problems

1. When the values of two ratios are equal, they are said to be in proportion and one is called proportional to the other.

2. Four quantities a, b, c and d are said to be in proportion or proportional when a: b : : c : d or a:b = c d [The symbol ‘: :’ stand for ‘as’]
a is called the 1st term of the proportions.

Similarly, b, c, and d are called the 2nd term, 3rd term and 4th term respectively.

So, \(\frac{1 \text { st term }}{2 \text { nd term }}=\frac{3 \text { rd term }}{4 \text { th term }}\)

⇒ 1st term x 4th term = 2nd term x 3rd term

i.e., The product of the extreme terms = The product of the two mean terms.

Example: 6 18 15: 45 are in proportional.

Read and Learn More WBBSE Solutions for Class 7 Maths

Here 6 x 45 18 x 15 = 270

Continued Proportion: Three quantities of the same kind are said to be in continued proportion when the ratio of the first to the second is equal to the ratio of the second to the third.

The second quantity is called a mean proportional between the 1st and 3rd.
If three quantities a, b and c are in continued proportion then a b : : b: c

⇒ \(\frac{a}{b}=\frac{b}{c} \Rightarrow b^2=a c\)

where b is called the mean proportional of a and c.

Example: 3:6 : : 6: 12

Here 3 x 12 = 6 x 6 = 36

Types of Proportions: There are two types of proportion

1.  Simple proportion or Direct proportion
2. Inverse proportion

1. Simple proportion or Direct proportion: Simple proportion constitutes of two ratios formed with simultaneous increase or decrease of two correlated quantities.

If two ratios a:b and c:d indicate the simultaneous increase or decrease, then the simple or direct proportion will be a: b : : c:d

2. Inverse proportion: If two ratios be such that one is equal to the inverse ratio of the other, then the proportion thus formed is an Inverse proportion.

Example: If two ratios a: b and c d then they form an inverse proportion.

i.e. a:b : : d:c [inverse of c:d]

or c: d : : b: a [inverse of a:b]

Wbbse Class 7 Maths Solutions

Question 1: Find if the pair of ratios given below are equal and also find if four members are in proportion

1. 6: 4 and 15: 10
2. 4-2: 1-4 and 21: 7
3. 5x: 6x and 3y: 4y [y ≠0, x ≠ 0]

Solution:

1.  6: 4 = 3: 2

15: 10  = 3: 2

∴ 64 and 15: 10 are equal.

Hence 6, 4, 15 and 10 are in proportion.
We can write 6: 4 : : 15: 10

2. 4.2: 1.4 = 3: 1

21: 7 = 3: 1

∴ 4.2: 14 and 21: 7 are equal.

Hence 4.2, 1.4, 21 and 7 are in proportion.
We can write 4.2: 1.4 : :  21: 7

3. 5x: 6x = 5: 6
3y: 4y = 3: 4

∴ 5x: 6x and 3y: 4y are not equal.

Hence 5x, 6x, 3y, 4y are not in proportion.

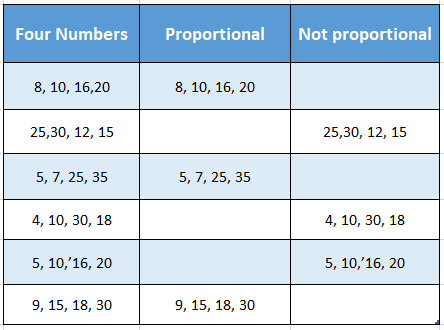
Question 2. Verify whether the following numbers are in proportion

1. 3, 4, 6, 8
2. 12, 18, 10, 15
3. 18, 8, 15, 6

Solution:

1. 3, 4, 6, 8
Here, product of extreme = 3 x 8 24 and product of means = 4 x 6 = 24

∴ Product of extreme = product of means
Hence the four members are in proportion.

2. 12, 18, 10, 15
Here, product of extreme = 12 x 15 = 180 and product of means = 18 x 10 = 180

∴ Product of extreme = product of means
Hence the four members are in proportion.

3. 18, 8, 15, 6
Here, product of extreme = 18 x 6 = 108 and product of means = 8 × 15 = 120

∴ Product of extreme product of means
So, the four members are not in proportion.

Question 3. Form different proportionality with 6, 8, 12, 16:

Solution:

Given Numbers 6, 8, 12, 16

Numbers	Extreme	Means	Product of extreme = Product of means	Proportion	Expressed as fraction
6, 8, 12, 16	6.16	8.12	6 x 16 = 8 x 12	6: 8 : : 12: 16	\(\frac{6}{8}=\frac{12}{16}\)
8, 6, 16, 12	8.12	6.16	8 x 12 = 6 x 16	8: 6 : : 16: 12	\(\frac{8}{6}=\frac{16}{12}\)
6, 12, 8, 16	6.16	12.8	6 x 16 = 12 x 8	6: 12 : : 8 : 16	\(\frac{6}{12}=\frac{8}{16}\)
12, 6, 16, 8	12.8	6, 16	12 x 8 = 6 x 16	12: 6 : : 16: 8	\(\frac{12}{6}=\frac{16}{8}\)

 

Question 4. Find the missing term from the given proportion 

1. *: 45 : 20
2. 6: * : : 10: 15
3. 8: 12 : : *: 24
4. 5: 10 : : 15: *

Solution:

1. *: 4 : : 5: 20

Let 1st term of the given proportion be x

So, x: 4 : : 5: 20

⇒ \(\frac{x}{4}=\frac{5}{20}\)

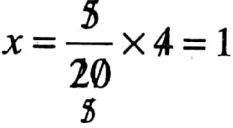
∴ 1st term is 1.

2. 6: * : : 10: 15

Let 2nd term is x

∴ 6: x : : 10:

⇒ \(\frac{6}{x}=\frac{10}{15}\)

⇒ 10x = 6 x 15

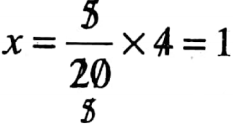
∴ 2nd term is 9.

3. 8: 12 : : *: 24

Let 3rd term is x
8: 12 : :  x: 24

⇒ \(\frac{8}{12}=\frac{x}{24}\)

⇒ 12x = 8 x 24

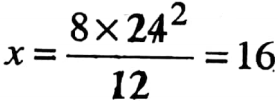
∴ 3rd term is 16.

4. 5: 10 : : 15: *

Let 4th term is x

⇒ \(\frac{5}{10}=\frac{15}{x}\)

⇒ 5x = 15 x 10

⇒ \(x=\frac{15 \times 10^2}{8}\)

⇒ x = 30

∴ 4th term is 30.

Wbbse Class 7 Maths Solutions 

Question 5. Find whether the following sets of numbers are in continued proportion and write the proportionality

1. 6, 8, 12
2. 5, 25, 125
3. 4, 10, 25

Solution:

1. 6, 8, 12

6 × 12 = 72 ≠(8)²

i.e., 1st term × 3rd term ≠ (mean term)²

So, 6, 8, 12 are not in continued proportion.

2. 5, 25, 125

5 × 125 = 625 = (25)²

i.e., 1st term x 3rd term = (mean)²

So, 5, 25 and 125 are in continued proportion.
The proportionality is 5 25 25: 125

3. 4, 10, 25

4 x 25 = 100 = 10²

1st term x 3rd term = (2nd term)²

So, 4, 10 and 25 are in continued proportion.
The proportionality is 4: 10 : : 10 : 25

Question 6: Of the three numbers in continued proportion, 1st and 2nd numbers are 16 and 20 respectively. Find the third number of this proportion.

Solution: Let the 3rd term of the continued proportion be x.
So, 16, 20 and x. are in continued proportion.

∴ 16: 20 : : 20: x

⇒ \(\frac{16}{20}=\frac{20}{x}\)

⇒ 16x = 20 x 20 = 400

⇒ \(x=\frac{400}{16}=25\)

∴ 3rd term is 25.

Question 7. Find the mean proportion of

1. 9 and 16
2. a and b
3. 1.5 and 13.5

Solution:
1. Let the positive mean proportion of 9 and 16 is x

∴ 9: x : : x: 16

⇒ \(\frac{9}{x}=\frac{x}{16}\)

⇒ x² =144
⇒x= √144 = 12

∴ Mean proportion 9 and 16 is 12

2. Mean proportion of a and b is ±√ab

3. Mean proportion of 1.5 and 13.5 is

\(\sqrt{1 \cdot 5 \times 13 \cdot 5}\)

 

= \(\sqrt{\frac{15}{10} \times \frac{135}{10}}\)

= \(\sqrt{\frac{15 \times 15 \times 3 \times 3}{10 \times 10}}\)

= \(\frac{15 \times 3}{10}=\frac{45}{10}\)

= 4.5

Wbbse Class 7 Maths Solutions

Question 8. If 6 men can do a piece of work in 20 days. Find in how many days will 12 men finish the same work.

Solution:

Given 6 men can do a piece of work in 20 days.

In the mathematical language, the problem is,

Men (number)
6
12

Time (days)
20
?

For a particular work, if the number of persons increases, less time is required to finish the work.

But if the number of people decreases, the time required will be increased.

∴ So the number of men and time are in inverse proportion.

In proportionality, we take the inverse of the relation.
∴ 12: 6 : : 20: ?

Product of extreme = product of means
∴ 12 x 4th term = 6 x 20

⇒ 4 th term =

Hence 12 men will take 10 days to finish the work.

Question 9: Ramesh babu used 24 ploughs to cultivate his whole land in 15 days. Find if he wanted to cultivate the same land in 10 days, how many ploughs he would have needed?

Solution:

Given

Ramesh babu used 24 ploughs to cultivate his whole land in 15 days.

In the mathematical language the problem is,

Time (days)
15
10

Number of ploughs
24
? (x) [say]

To cultivate the whole land, as time decreases, the required number of ploughs will be increased. So the time and number of ploughs are in inverse proportion.

So, 10: 15 : : 24: x

⇒ \(\frac{10}{15}=\frac{24}{x}\)

⇒ 10 x = 24 x 15

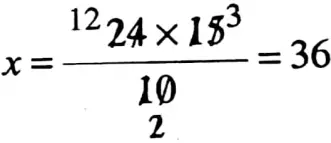
∴ 36 ploughs would have been needed.

Wbbse Class 7 Maths Solutions

Question 10. In a flood relief camp, there is the provision of food for 4000 people for 190 days. After 30 days, 800 people went away elsewhere. Find for how many days the remaining food lasts for the remaining people in this camp.

Solution:

Given

In a flood relief camp, there is the provision of food for 4000 people for 190 days. After 30 days, 800 people went away elsewhere.

Let the required number of days be x.

In the mathematical language, the problem is,

No of people (by heads)
4000
4000 -800 = 3200

Time (days)
190 – 30 =160
x

As the number of people decreases therefore the certain quantity of food will cover more number of days for the same heads. So the number of people and the number of days are inversely proportional so,

3200: 4000 : : 160: x

⇒ \(\frac{3200}{4000}=\frac{160}{x}\)

∴ That food will go on for 200 days for 3200 people.

Question11. When water freezes to ice, its volume increases by 10%. Find the ratio of a certain volume of water and its corresponding volume of ice.

Solution:

Given

When water freezes to ice, its volume increases by 10%

100 cubic units of water when freezes to ice, its volume becomes (100 + 10) cubic units or 110 units.

So the ratio of certain volume of water and its corresponding volume of ice is, 100: 110 or 10: 11

Question 12. The cost of 5 tables is 8000. Calculate the price of 8 tables.

Solution:

Given  The cost of 5 tables is 8000.

In the mathematical language the problem is,

No of Tables
5
8

Price of Tables (in rupees)
8000
?

If the number of tables increases the price will increases. If the number of tables decreases price will decrease.

So the number of tables and the price of the tables are directly proportional.

∴ 5: 8 : : 8000: ?

∴ Cost of tables (?) =

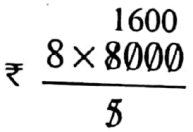
= ₹12800

The price of 8 tables = ₹12800

Question 13. The ratio of the ages of father and son is 5: 2. After 10 years the ratio of their ages will be 2: 1. Find the present ages of father and son.
years.

Solution:

Given

The ratio of the ages of father and son is 5: 2.

Let the father’s age is 5x years and son’s age is 2x years.

[where x is the common multiple and x > 0]

After 10 years the father’s age will be (5x + 10) years and son’s age will (2x + 10)

According to the conditions,

\(\frac{5 x+10}{2 x+10}=\frac{2}{1}\)

Wbbse Class 7 Maths Solutions

⇒ 5x+10 = 2(2x+10)

⇒ 5x+10 = 4x = 20

⇒ 5x – 4x = 20 – 10

⇒ x = 10

∴ The present age of the father is (5 x 10) years or 50 years and the age of the son is (2 x 10) years or 20 years.

 

Class 7 Math Solution WBBSE Proportion

Proportion Exercise 3.1

Question 1. Let’s find if the pair of ratios given below are equal and also find if four members are in proportion.

1. 7: 2 and 28: 8

Solution:

Here 7: 2 = (7 × 4) : ( 2× 4) (Multiplying both by 4)

= 28: 8

∴ 7 : 2:: 28: 8

∴ They are proportional. ,

2. 9: 7 and 18: 14
Solution:

Here 9 : 7 = (9 × 2) : (7 × 2) (Multiplying both by 2)

= 18 : 14

∴  9 : 7: : 18: 14

∴  They are proportional.

3. 1.5 : 3 and 4.5: 9.
Solution :

Here 1 .5 : 3 = (1 .5 x 3) : (3 x 3) (Multiplying both by 3)

= 4.5 : 9

∴  1 .5 : 3 : : 4.5 : 9

∴  They are proportional.

4. 7 : 3 and 5 : 2.
Solution:

Here 7:3≠ 5:2

∴  They are not in proportional.

5. 3ab : 4aq and 6b : 8q.
Solution :

Here \(\left(3 a b \times \frac{2}{a}\right)\) : \(\left(4 a b \times \frac{2}{b}\right)\) = 6b : 8q

∴ 3ab ; 4aq : : 6b :.8q

∴ They are in proportion

6. 5.2: 6.5 and 4: 5
Solution:

Here \(\frac{5.2}{1.3}: \frac{6.5}{1.3}\) = 4:5

∴ 5.2: 6.5 :: 4 : 5

∴ They are in proportion.

7. 3y : 7y and 12 p : 28p.
Solution :

Here \(\left(3 y \times \frac{4 p}{y}\right):\left(7 y \times \frac{4 p}{y}\right)\)

= 12p :28p

∴ 3y : 7y : : 12p : 28y

∴ They are in proportion.

8. 5pq : 7pr and 15s : 21 q [ here a, q, y, p, r are not zeros ]
Solution :

Here 5pq : 7pr ≠ 15s : 21 q

∴ They are not in proportion.

Question 2. The length and breadth of a rectangular figure are 10 cm and 6 cm respectively. The length and breadth of figure are increased by 2 cm. Let’s find if the ratios of length to breadth remain same.
Solution :

Given

The length and breadth of a rectangular figure are 10 cm and 6 cm respectively. The length and breadth of figure are increased by 2 cm.

Length : Breadth = 10 cm : 6 cm = 5 : 3

Now, New length =.(10 + 2) cm = 12 cm.

New breadth (6 + 2) cm = 8 cm.

∴ New length : New breadth = 12 cm : 8 cm = 3 : 2

Here the length: Breadth are not the same.

Class 7 Math Solution WBBSE

Question 3. Paranbabu bought 500 gm of sugar for Rs. 17.50 and Deepenbabu bought 2 kg of sugar for Rs. 70. Let’s find if the 12p ; 28py amounts of sugar and their prices are in proportion.
Solution :

Given

Paranbabu bought 500 gm of sugar for Rs. 17.50 and Deepenbabu bought 2 kg of sugar for Rs. 70.

Paranbabu bought 500 gm sugar for Rs. 17.50

∴ Here the cost price = Rs. 35 per kg.

Deepenbabu bought 2 kg sugar for Rs. 70.

∴ Here the cost price = Rs. 35 per kg.

∴ They bought equal quantity of sugar at same price

Question 4. Fill in the blank squares :

1. 5 : 7 : : 25 : 35
Solution:

⇒ 5 : 7 : : 25 : 35

As 5 × 5 = 25

7× 5 = 35

2. 6 : 7 : : 30 : 35
Solution:

⇒ 6 : 7 : : 30 : 35

As 6 × 5 = 30

7 × 5 = 35

3. 21 : 28 : : 3 : 4
Solution:

21 : 28 : : 3 : 4

⇒  As \(\frac{21}{7}\) = 3

= \(\frac{28}{7}\) = 4

4. 9 : 24 : : 3 : 8
Solution:

9 : 24 : : 3 : 8 A

As \(\frac{9}{3}\) = 3

⇒ \(\frac{24}{3}\) = 8

Class 7 Math Solution WBBSE Proportion Exercise 3.2

Question 1. Let’s verify whether 7, 5, 14 and 10 are in proportion.
Solution :

Given

7, 5, 14 and 10

Here product of extreems = 7 × 10 = 70

And product of means = 5 × 14 = 70

∴ Product of extremes = product of means

Hence, the four numbers are in proportion.

Question 2. Let’s verify whether 10, 5, 14 and 7 are in proportion.
Solution :

Given

10, 5, 14 and 7

Here the product of extreme = 10 × 7 = 70

And product of means = 5 × 14 = 70

∴  Product of extremes = Product of means

Hence, the four numbers are in proportion.

Question 3. Let’s verify whether 14, 5, 10 and 7 are in proportion.
Solution :

Given

14, 5, 10 and 7

Here product of extremes = 1 4 × 7 = 98

And product of means = 5 × 10 = 50

∴ Product of extremes

Hence, the four numbers are Product Not in proportion.means

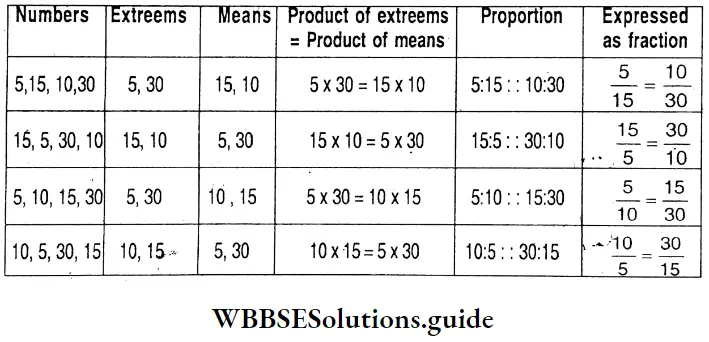
Question 4. Let’s prepare table as above and form different proportion with 5, 15, 10 and 30.

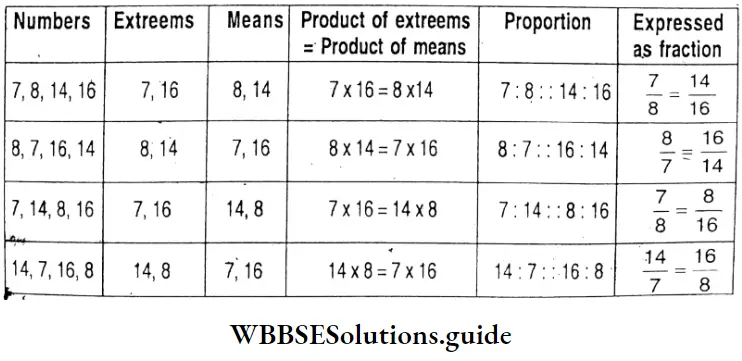
Question 5. Let’s prepare table as above and form different proportions with 7, 8, 14, 16.
Solution:

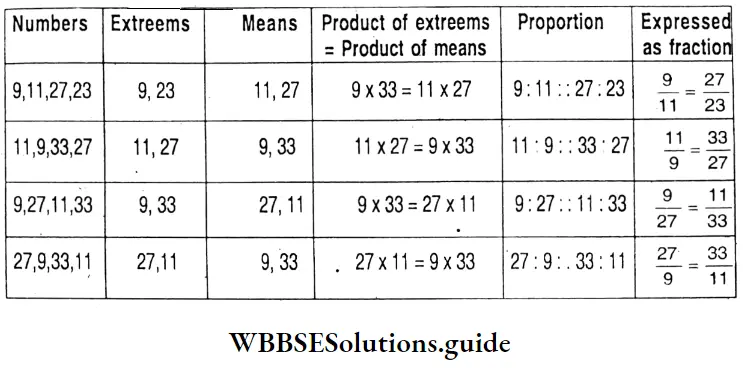
Question 6. Let’s form different proportions with 9, 11, 27 and 33
Solution:

Class VII Math Solution WBBSE Proportion Exercise 3.3

Question 1. Let’s find whether the following sets of numbers are in continued proportion, and let’s write the proportionality :

1. 5, 10, 20
Solution:

⇒ 5, 10, 20

Here 5 ×  20 = 100= (10)²

Hence 1 st term x 3rd term = (2nd term)² or (mean)²

∴ 5, 10 and 20 are in continued proportion.

∴ 5: 10: : 10: 20

2. 8, 4, 2
Solution: 

⇒ 8, 4, 2

Here 8 × 2 = 16= (4)²

i.e. 1st term x 3rd term = (2nd term)² or (mean)²

∴ 8, 4, and 2 are in continued proportion.

∴ 8: 4 :: 4 : 2

3. 7, 14, 28
Solution:

⇒ 7, 14, 28

Here 7× 28 = 196= (14)²

Hence, 1st term x 3rd term = (2nd term)² or (mean)²

∴ 7, 14, and 28 are in continued proportion.

∴  7: 14 : : 14: 28

4. 81, 9, 18
Solution :

⇒ 81, 9, 18

Here 81 x 18 = 1458

Henc# 1st term x 3rd term= (2nd term)²

∴ 81, 9 and 18 are not in continued proportion.

5. 4, 6, 12
Solution :

⇒ 4, 6, 12

Here 4 x 12 = 48 ≠ (6)²

Hence, 1st term x 3rd term ≠ (2nd term)²

∴ 4, 6 and 12 are not in continued proportion.

6. 4, 10, 25
Solution :

⇒ 4, 10, 25

Here 4 × 25 = 100 = (10)²

Hence, 1st term x 3rd term = (2nd term)² or (mean)²

∴ 4, 10, and 25 are in continued proportion

∴ 4: 10 :: 10 : 25

Class VII Math Solution WBBSE Proportion Exercise 3.4

Proportion Exercise 3.5

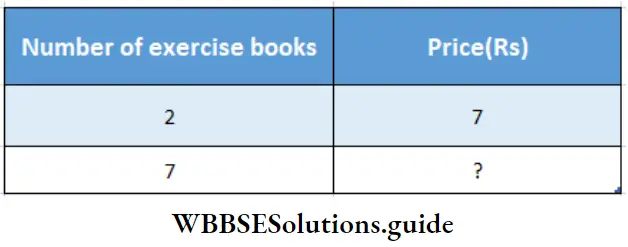
Question 1. Sumit bought 2 exercise books for Rs. 1 4. Let’s find how much he will pay for 7 such exercise books.
Solution :

Given

Sumit bought 2 exercise books for Rs. 1 4.

Here no. of exercise books and cost price are in direct proportion

∴  2 : 7 : : 14: ?

Or, 2 × 4th term = 7 × 14

∴ 4th term = \(\frac{7 \times 14}{2}\) = 49

∴ Price of 7 exercise book = Rs. 49.

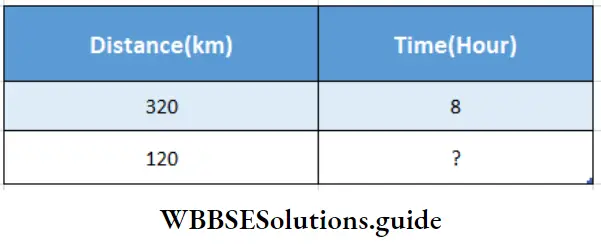
Question 2. A jeep covers a distance of 320 km in 8 hours, keeping the same speed, let’s find how long the jeep will take to cover a distance of 120 km.
Solution :

Given

A jeep covers a distance of 320 km in 8 hours,

Here distance and time are in direct proportion.

∴ 320 : 120: : 8 : ?

∴ 320 × 4th term = 120 × 8

∴ 4th term = \(\frac{120 \times 8}{320}\) = 3

∴ Time required to cover 120 km = 3 hour

Question 3. 720g of chromium is needed to make 6kg of stainless steel. Let’s find how much cromium will be needed to make 11 kg of stainless steel.
Solution :

Given

720g of chromium is needed to make 6kg of stainless steel.

Quantity of stainless steel (kg) Quantity of Cromium (gm) .

Here quantity of stainless steel & quantity of cromium are in direct proportion.

∴ 6:11 : : 720 : ?

∴  6 × 4th term = 11 x 720

∴  4th term = \(\frac{11 \times 720}{6}\)

= 1320 gm = 1.32 kg.

∴  1.32 kg of cromium will be needed.

Question 4. There are 3 litres of syrup in 10 litre of a soft drink (sherbat). Let’s find how much syrup will be required to make 5 litres of soft drink.
Solution :

Given

There are 3 litres of syrup in 10 litre of a soft drink (sherbat).

Volume of Soft drink (litre) Volume of syrup (litre)

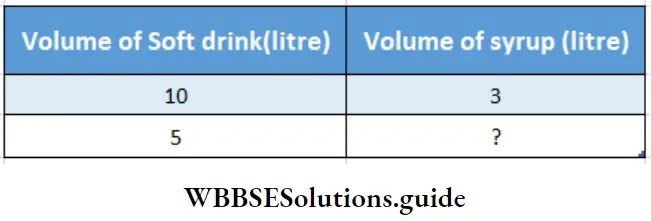
Here volume of soft drink & volume of syrup are in direct proportion.

∴ 10 : 5 : : 3 : ?

∴  10 × 4th term = 5 × 3

∴  4th term = \(\frac{5 \times 3}{10}=\frac{3}{2}\)

= 1.5 litre of syrup is required.

Class Vii Math Solution WBBSE Question 5. Let me form a practical problem on direct proportion and try to solve it.

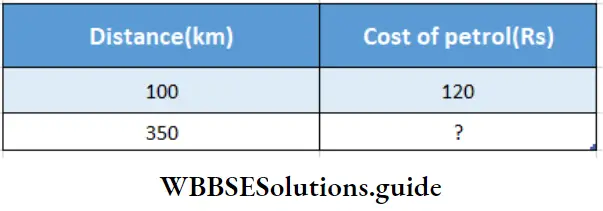
A car can travel 100 km on the cost of petrol of Rs. 120

1. How much would the petrol cost for a journey of 350 km?
2. How many would they travel for the cost of Rs. 300 petrol?

1. How much would the petrol cost for a journey of 350 km?
Solution:

Here the distance travelled & the cost of petrol are in direct proportion.

100 : 350: : 120: ?

∴ 350 × 120

∴ 100 x 4th term = 350 x 1 00

∴ 4th term = \(\frac{350 \times 120}{100}\)  = 420

∴ To travel 350 km. cost of petrol will be Rs. 420.

Question 6. How many would the can travel for the cost of Rs. 300 petrol?
Solution:

Here the cost of petrol & the distance travelled are in direct proportion.

∴ 120 : 300: :100: ?

∴ 120 ×  4th term = 300 × -1 00

∴ 4th term = \(\frac{300 \times 100}{120}\) = 250

With cost of Rs. 300, petrol, one can go = 250 km

WBBSE Class 7 Math Solution Proportion Exercise 3.6

Question 1. Let’s complete the table given below

Question 2. 8 men can do a piece of work in 15 days. Let’s find in how many days will 10 men finish the same work.
Solution :

Given

8 men can do a piece of work in 15 days.

For doing a work if the number of men were increased the time required would decrease.

∴ Number of men and time (no. of days) are in inverse proportion.

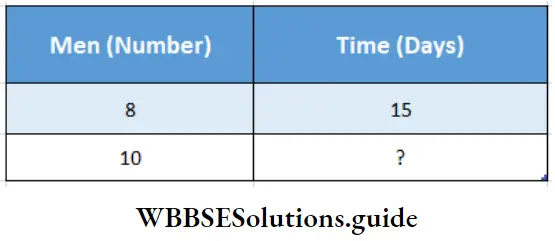
In proportionality let’s take the inverse of relation.

∴ 10: 8 = 15: ?

∴ Product of extremes = Product of means

10 ×  4th term = 8 ×15

∴  4th term = \(\frac{8 \times 15}{10}\)

Hence, 10 men will take 12 days to finish the work.

Question 3. 1 2 men had provision of food for 20 days. Let’s find, if there are 40 men, how long will the provision last?
Solution:

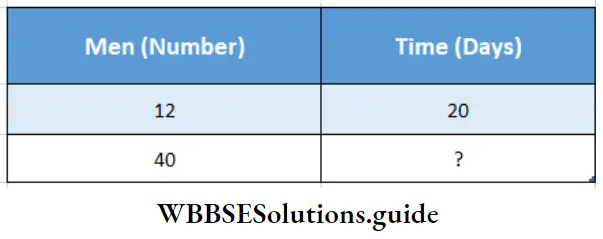
Given

12 men had provision of food for 20 days.

Here if the number of men increased, no. of days decreased.

A number of men and a number of days are in inverse proportion.

Let us take the inverse relation.

12 : 40 = 7 × 20

Product of extreems = Product of means

12 × 20 = 40  × ?

∴ 4th term = \(\frac{12 \times 20}{40}\) = 6

∴  For 40 men provision last for 6 days.

Question 4. Arunbabu used 1 6 ploughs to cultivate his whole land in 1 0 days. Let’s find, if he wanted to cultivate the same land in 8 days, how many ploughs he would have needed.
Solution :

Given

Arunbabu used 16 ploughs to cultivate his whole land in 1 0 days.

No. of days No. of Ploughs

Here no. of days & no. of ploughs are in inverse proportion.

10 : 8 = ? : 16

∴ Product of extrems = Product of means

10 × 16 = 8 × ?

∴ 4th term = \(\frac{10 \times \cdot 16}{8}\) = 20

∴ 20 ploughs are required to cultivate the same land.

Question 5. In a flood relief camp, there is a provision of food for 4000 people for 1 90 days. After 30 days, 800 people went away elsewhere. Let’s find for how many days the remaining food lasts for the remaining people in this camp.
Solution:

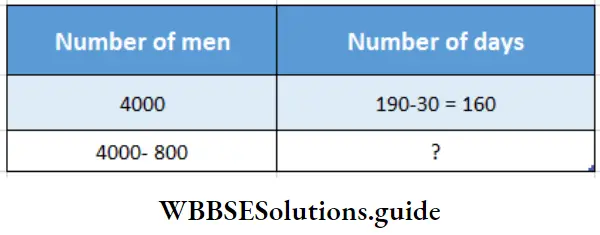
Given

In a flood relief camp, there is a provision of food for 4000 people for 1 90 days. After 30 days, 800 people went away elsewhere.

Here No. of men decreased, so no. of days will increase.

No. of men and no. of days are in inverse proportion.

3200 : 4000= 160 : ?

.;. Product of extremes- Product of mean

3200 x? = 4000 × 160

= \(\frac{4000 \times 160}{3200}\)

= 200

∴ Remaining food last for 200 days.

Question 6. The cost of 3 umbrellas or 1 chair is Rs. 600. Let’s calculate the price of 2 umbrellas and 2 chairs.
Solution :

Given

The cost of 3 umbrellas or 1 chair is Rs. 600.

Cost of 1 chair = Cost of 3 umbrellas

Cost of 2 chair = Cost of 3 × 2 = 6 umbrellas.

Cost of 2 umbrellas + 2 chairs =-2 + 6 = 8 umbrellas.

Here no. of umbrella & the price are in direct proportion.

∴ 3 : 8 = 600 : ?

∴  i.e Product of extremes = Product of means

3 × ? = 8 ×  600

∴ Price = \(\frac{8 \times 600}{3}\) = 1600

∴ Required price = Rs. 1600.

WBBSE Class 7 Math Solution Question 7. Let’s find the ratio of the number of students present and number of students absent today in our class. We also find the ratio of number of students present and the number of students absent today in class six. Let’s find in the ratios are equal and also find if the four numbers are in proportion.
Solution :

Let in class 7 no. of student present & absent are 42 & 8.

Ratio of number of students absent today in class 7

= 42 : 8 = 21 : 4

Again in class 6 no. of student present & absent are 40 & 1 0

Ratio of number of student present and number of student absent to day in Class 6 = 40: 1 0 = 4 : 1

These two ratios are not equal,

And the four numbers (42, 8, 40, 10) are not in proportional.

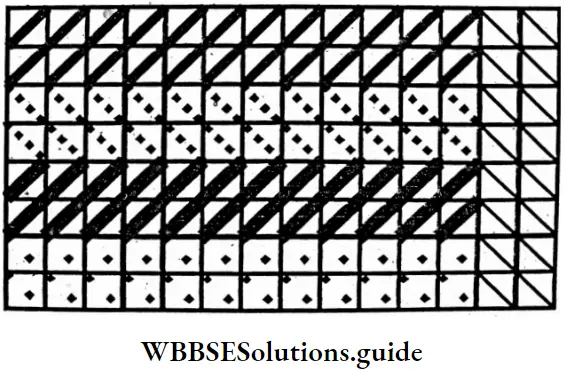
Question 8. Let us count the number of squares of different colours and answer the questions given below.

1. Ratio of red squares and blue squares.
Solution: 9:2.

2. What is the ratio of brown & violet squares?
Solution: 12:13.

What is the ratio of red & green squares?
Solution: 3 :2.

Ratio of brown and yellow squares?
Solution: 3 :2.

Which four of the coloured squares are in proportion?
Solution: Red, green, brown & yellow.

Question 9. In two types of ‘sherbet’ the ratios of syrup and water are 2: 5 and 6:10. Let’s find, which one is sweeter.
Solution :

Given

In two types of ‘sherbet’ the ratios of syrup and water are 2: 5 and 6:10.

In 1st type of Sherbat, Syrup : Water = 2:5= \(\frac{2}{5}\)

In 2nd type of Sherbat, Syrup : Water = 6:10 = 3:5= \(\frac{3}{5}\)

∴ 2nd one is more sweeter.

Question 10. When water freezes to ice, its volume inceases by 1 0%. Let’s find the ratio of a certain volume of water and its corresponding volume of ice.
Solution :

Given

When water freezes to ice, its volume inceases by 1 0%.

Set the volume of water = 100 cc.

∴ The volume of ice = \(\left(100+\frac{10}{100} \times 100\right) \mathrm{cc}\)

= (100 + 10) cc. = 110 cc.

∴ Ratio of volume of water and corresponding volume of ice

= 1 00 cc : 1 1 0 cc =10:11.

Ratio of volume of water and corresponding volume of ice =10:11.

WBBSE Class 7 Math Solution Question 11. My age is 12 years and my father’s age is 42 years. Let’s find the ratio of our ages.
Solution :

Given

My age 12 years

My father’s age = 42 years

∴The ratio of my age and my father’s age

= 12 year : 42 years = 2:7.

Question 12. The ratio of storybooks and textbooks of Preetam is 2: 5. If Preetam has 4 story books, then let’s find how many textbooks he has.
Solution :

Given

The ratio of story books and textbooks of Preetam = 2:5

⇒  \(\frac{\text { No. of story books }}{\text { No. of textbooks }}=\frac{2}{5}\)

⇒ \(\frac{4}{\text { No. of text books }}=\frac{2}{5}\)

Or, 2 x number of textbooks = 4 × 5

Number of text books\(\frac{4 \times 5}{2}\) = 10

Question 13. For making a flower garland of china roses (Jaba) and Indian marigold (gada), 105 of these flowers were collected. If the ratio of chinaroses and marigold is 3 : 4, let’s find how many china roses and marigolds are there. Let’s also find how many more chinaroses must be collected so that the ratio of these two types of flowers become equal.
Solution :

Given

For making a flower garland of china roses (Jaba) and Indian marigold (gada), 105 of these flowers were collected. If the ratio of chinaroses and marigold is 3 : 4,

Total No. of flowers = 105

The ratio of no. of Jaba flowers and no. of gada flowers = 3:4 =

∴ No. of Chinaroses (Jaba) flowers = \(\frac{3}{7}\) × 105 = 45

Number of Marigold (gada) flowers= \(\frac{4}{7}\) × = 60

To make the ratio of two types of flowers equal,

Number of  chinaroses (Jaba) flowers required = 60 – 45 = 1 5.

Question 14. Let the small squares in the square given below, are coloured according to your own will with 5 different colours from those 5 types of coloured squares, let’s choose any pair of colours and find the ratio between their number of squares. Of these ratios, also identity the ratios of greater inequality, ratio of lesser inequality and ratio of equality. Out of these ratios, if the numbers of four different coloured squares are found in proportion, then note that proportionality too.
Solution :

Given

Let the small squares in the square given below, are coloured according to your own will with 5 different colours from those 5 types of coloured squares,