WB Class 7 Math Solution Arithmetic Chapter 6 Time And Distance Exercise 6 Solved Problems
⇒ Speed: When a moving body changes its position, it covers a certain distance at a certain time. The rate of change of distance is known as speed.
⇒ In other words, the distance covered by a moving body in a unit of time is known as speed. The distance covered is directly proportional to the time taken by the body.
1. \(\text { Speed }=\frac{\text { Distance covered }}{\text { Time required to cover the distance }}\)
2. \(\text { Time required }=\frac{\text { Distance covered }}{\text { Speed }}\)
3. Distance covered x = Speed x Required time.
Relative speed: Relative speed is the speed of one object relative to another object.
1. If two objects move in the same direction, then relative speed = difference of their speeds.
2. If two objects move in the opposite direction, their relative speed = the sum of their speeds.
Read and Learn More WBBSE Solutions for Class 7 Maths
Question 1. Choose the correct answer
1. Ramen covered a distance of 276 km in 6 hours in a bus. The speed of the bus in km/ hr is
1. 48 km/hr
2. 46 km/hr
3. 40 km/hr
4. 42 km/hr.
Solution:
Given
⇒ Ramen covered a distance of 276 km in 6 hours in a bus.
\(\text { Speed }=\frac{\text { Distance covered }}{\text { Time required }}\)=\(\frac{276}{6}\) km/hr
= 46 km/hr
So the correct answer is 2. 46 km/hr
Wbbse Class 7 Maths Solutions
2. A train of length 100 m. moving with a speed of 60 km / m. passes a tree. How long will it take to do so?
1. 4 sec
2. 5 sec
3. 6 sec
4. 7 sec
Solution:
Given
⇒ A train of length 100 m. moving with a speed of 60 km / m. passes a tre
⇒ To cross a tree, the train will have to travel a distance equal to its own length. So here the train will have to travel 100 m.
The speed of the train is 60 km/h.
60 km = 60 × 1000 m = 60000 m
1 hour = (60 x 60) sec = 3600 sec.
i.e., 60000 m is covered by the train in 3600 sec.
1 m is covered by the train in \(\frac{3600}{60000}\) sec
100 m is covered by the train in
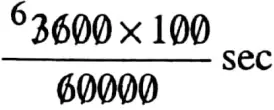
= 6 sec
∴ The required time is 6 sec.
So the correct answer is 3. 6 sec
3. A train runs at the rate of 40 km an hour. How far will it run in 21 minutes?
1. 7 km
2. 14 km
3. 18 km
4. 20 km.
Solution:
Given
⇒ A train runs at the rate of 40 km an hour.
⇒ In the mathematical language
Time (mins)
60
21
Distance (km)
40
?
⇒ Speed being constant the time and distance are in direct proportion.
∴ 60: 21 : : 40 : ? (Required distance)
∴ Required distance(4th Proportion) =

= 14 km
⇒ So the correct answer is 2. 14 km
Wbbse Class 7 Maths Solutions
Question 2. Write true or false
1. A bus covers a distance of 110 km in 3 hrs 40 mins. The speed of the bus is 30 km. / h.
Solution:
Given
⇒ A bus covers a distance of 110 km in 3 hrs 40 mins.
⇒ 3 hrs 40 mins (3 x 60+40) mins. = 220 mins.
⇒ In mathematical language, the problem is
Required time (mins)
220
60
Distance covered (km)
110
?
⇒ The required time and distance covered are directly proportional.
So 220: 60 : : 110: ? (Required distance)
∴ Required distance (4 th proportion) =

Speed of bus is 30 km / h
So the statement is true.
WB Class 7 Math Solution 2. A man takes 12 hours to travel 72 km. He takes 5 hours to travel 48 km. Let he takes x hours to travel 48 km.
Solution:
Given
A man takes 12 hours to travel 72 km. He takes 5 hours to travel 48 km.
In mathematical language the problem is
Distance covered (km)
72
48
Time taken (hr)
12
x
The time taken and the distance covered is directly proportional.
So, 72: 48 : : 12: x
⇒ \(\frac{72}{48}=\frac{12}{x}\)
⇒ 72x = 12 x 48

⇒ x=8
He takes 8 hours to travel 48 km. So the statement is false.
Question 3. Fill in the blanks
1. The distance covered in 3 hrs at 5.6 km/hr is _______ km
Solution: The distance covered in 1 hour is 5.6 km
The distance covered in 3.5 hours is (3 x 5.6) km = 16.8 km
2. The distance covered by a moving body is the product of its — and the time taken
Solution: Speed.
Wbbse Class 7 Maths Solutions
Question 4. To pass a bridge of length 230 m a train of length 170 m took 20 sec. Calculate to find how long will this train take to pass a 110 m long platform.
Solution:
Given
To pass a bridge of length 230 m a train of length 170 m took 20 sec.
When a train crosses a bridge, then the train has to cover a distance of its own length + the length of the bridge. That is (230+ 170) m or 400 m.
If a train crosses a platform of length 150 m, then the train has to cover a distance is (170+110) m or 280 m.
In mathematical language, the problem is
Distance (metre)
400
280
Time (sec)
20
? (x)[say]
Speed remains constant, and time and distance are in direct proportion.
∴ 400: 280 : : 20: x
⇒ \(\frac{400}{280}=\frac{20}{x}\)
⇒ 400x = 20× 280

⇒ x = 14
∴ The train would take 14 secs to cross the platform.
Question 5. A train passes two brides of lengths 210 m and 122 m in 25 sec and 17 sec respectively. Calculate the length and speed of the train.
Solution:
Given
A train passes two brides of lengths 210 m and 122 m in 25 sec and 17 sec respectively.
Let the length of the train be x m. When the train crosses a bridge of length 210 m then the train has to cover a distance of length (210 + x) m.
Similarly to cross the second bridge of length 122 m; the train has to cover a distance of length (122 + x) m.
In the mathematical language, the problem is,
Time taken (sec)
25
17
Distance covered (m)
(x + 210)
(x + 122)
Speed remains constant, time and distance are in direct proportion.
∴ 25: 17 : : (x + 210): (x + 122)
⇒ \(\frac{25}{17}=\frac{x+210}{x+122}\)
⇒ 25 (x+122) = 17 (x + 210)
⇒ 25x + 3050 = 17x+ 3570
⇒ 25x – 17x = 3570 – 3050
⇒ 8x= 520

⇒ x= 65
∴ The length of the train is 65 meter.
In 25 sec the train travels (65+ 210) m or 275 m
In 1 sec the train travels \(\frac{275}{25}\) m
In 1 hr or 3600 sec the train travels

= 39600 mt = 39.6 km
∴ The length of the train is 65 mt. and speed is 39.6 km/hr.
Wbbse Class 7 Maths Solutions
Question 6. Two trains of lengths 170 m and 180 m are approaching each other with speeds of 45 km/hr and 30 km/hr along two tracks. Calculate how long will they take to pass each other after meeting.
Solution:
Given
Two trains of lengths 170 m and 180 m are approaching each other with speeds of 45 km/hr and 30 km/hr along two tracks.
After the two trains meet, they would pass each other i.e., the two trains would simultaneously pass a distance equal to sum of their own length.
∴ The distance two trains will cover (170 + 180) m or 350 m.
When the two trains travel in opposite directions, in 1 hour they would cover a distance of (45+30) km or 75 km or 75000 m.
1 hour = 3600 sec.
In the mathematical language the problem is,
Distance (metre)
75000
350
Time (sec)
3600
?
Time and distance are direct proportion.
∴ 75000: 350 : : 3600 ?
∴ Time taken

= \(\frac{84}{5}\) sec. = 16.8 sec
∴ The train will pass each other in 16.8 sec.
Alternative Method:
75000 metres is covered in 3600 sec
1 metre is covered in \(\frac{3600}{75000}\) sec
350 metre is covered in
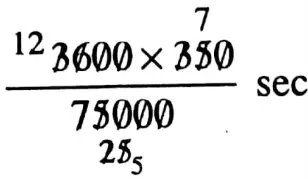
= \(\frac{84}{5}\) sec = 16.8 sec
WB Class 7 Math Solution Time And Distance
Time And Distance Exercise 6
Question 1. On Saturday, I was cycling at a speed of 13 km/hr. I covered a certain distance in 2 hrs. On Sunday cycling at the same time at a speed of 11 km/hr.I covered a certain distance. Let us find out on which day. I could travel a distance more in 2 hours and how much? Hence, keeping time constant, try to find a relation between speed and distance (direct or inverse proportion)
Solution :
Given
On Saturday, I was cycling at a speed of 13 km/hr. I covered a certain distance in 2 hrs. On Sunday cycling at the same time at a speed of 11 km/hr.I covered a certain distance.
My speed of cycling is 13 km/hr.
∴ I will cover in 2 hrs. = 13 × 2 = 26 km.
Next day Sunday my speed is 1 1 km/hr.
∴ I will cover in 2 hrs. on Sunday = 2 ×11 =22 km.
∴ On Saturday I cover 26 – 22 = 4 km more.
∴ Speed & distance are in direct proportion.
Question 2. On Monday,l went to market cycling at a speed of1 2 km/hr. But on Tuesday) went to market cycling at a speed of 15 km/hr. If the distance between my house and market is 2km, then let’s us find, on which day. I took less time to reach the market. Hence, keeping distance same, let’s form a relation between speed and time required (direct or inverse proportion).
Solution :
For Monday:
Given
On Monday,l went to market cycling at a speed of1 2 km/hr. But on Tuesday) went to market cycling at a speed of 15 km/hr. If the distance between my house and market is 2km,
Speed = 12 km/hr.
Distance = 2 km.
Time required = \(\frac{\text { Distance Covered }}{\text { Speed }}\)
= \(\frac{2 \mathrm{~km}}{12 \mathrm{~km} / \mathrm{hr} .}=\frac{2}{12} \mathrm{hr}\)
= \(\frac{1}{6} \mathrm{hr}\) hr.
= \(\frac{1}{6} \times 60\) min.
= 10 min
For Tuesday:
Speed = 15 km/hr. Distance = 2 km
Time required = \(\frac{\text { Distance Covered }}{\text { Speed }}\)
= \(\frac{2 \mathrm{~km}}{15 \mathrm{~km} / \mathrm{hr} .}=\frac{2}{15} \mathrm{hr}\)
= \(\frac{2}{15} \times 60\) min.
= 8 min
∴ On Tuesday I took less time to reach the market (10m – 8m) = 2m
Here as the distance same, when speed in increasing time is decreasing i.e. speed & time are in inverse proportion.
Question 3. Keeping speed constant, let’s find the relation between time and distance [let’s prepare a story and find the relation]
Solution :
A passenger train of length 156 meters is traveling with a speed of 24 km/hr. Find the time taken by this train to cross a goods train of length 1 64 metres,’ which .is at rest by the side of the path of the passenger train.
Total length of the two trains = (156m + 164m) = 320 meters
Speed the train = 24 km/hr. i.e. the train goes 24 km = 24000 m in 1 hr
= 60 × 60 = 3600 sec
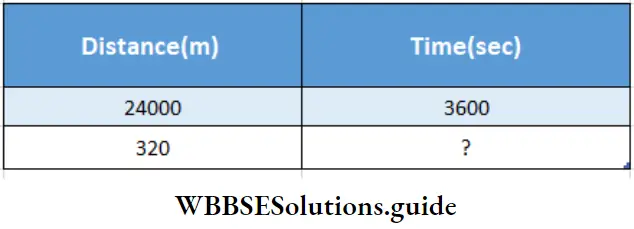
Here distance & time are in direct proportion.
∴ 24000 : 320: : 3600:?
Time = \(\frac{320 \times 3600}{24000}\)
= 48 sec
The relation between time and distance= 48 sec
Question 4. I covered a distance of 12 km in 40 min in a bus. Let’s find the speed of the bus in km/hr.
Solution :

Given
I covered a distance of 12 km in 40 min in a bus.
Time and distance are in direct proportion
40 : 60: : 12 : ?
Distance = \(\frac{60 \times 12}{40}\)km
= 18 km
WB Class 7 Math Solution Question 5. A train of length 100m, moving with a speed of 60 km/hr. passes a tree. How long will it take to do so, lets calculate.
Solution:
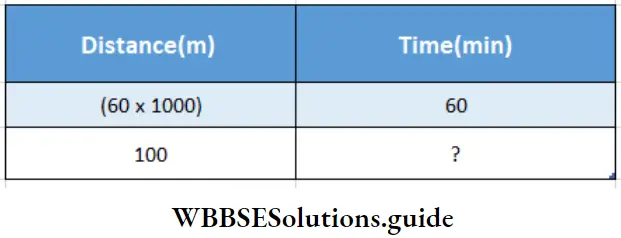
Given
⇒ A train of length 100m, moving with a speed of 60 km/hr. passes a tree.
⇒ Distance and time are in direct proportion
⇒ (60 × 1000): 100:: 60:?
⇒ Time = \(\frac{100 \times 60}{60 \times 1000}\)
= \(\frac{1}{10}\) min
= \(\frac{1}{10} \times 60\)
= 6 sec
It will take 6 sec. to do so.
Question 6. Moving with a uniform speed a taxi takes 6km 12 min to cover a distance of 217 km. Let us calculate how much time it would take to cover a distance of 273 km. (Mention the relation to calculate).
Solution :
Given
⇒ Moving with a uniform speed a taxi takes 6km 12 min to cover a distance of 217 km.
⇒ 6 hr 12 min = (6 × 60 + 12) min = 372 min

Here, Distance and time are in direct proportion.
217: 273:: 372:?
Time = \(\frac{273 \times 372}{217}\)
It would take 7 hr. 48 m. to cover the distance.
Question 7. Today, Ayanda of our locality covered a distance of 100 km in 2 hrs 5 min. on his motorbike. But Shibuya covered the same distance on his cycle in 6 km 40 min. Let’s write the ratio of their speeds.
Solution:
Given
Today, Ayanda of our locality covered a distance of 100 km in 2 hrs 5 min. on his motorbike. But Shibuya covered the same distance on his cycle in 6 km 40 min.
2 hrs 5 min = (120 + 5) min
6 hrs 40 min = (360 + 40) min = 400 min
Ayanda covered in 125 min a distance of 1 00 km. = \(\frac{125}{100}\) min
∴ He covered in 1 min a distance of km.
∴ His speed is \(\frac{125}{100}\) km/min = \(\frac{4}{5}\) km/rnln.
Shibuda covered in 400 min a distance of 100 km.
∴ He covered in 1 min a distance of \(\frac{100}{400}\) km.
∴ His speed is \(\frac{100}{400}\) km/min. = \(\frac{100}{400}\) km/min.
∴ Ratio of their speed = \(\frac{100}{400}\) km/min : \(\frac{100}{400}\) km/min.
⇒ \(\frac{4}{5}\): \(\frac{1}{4}\) = 16:5
Question 8. Moving with a uniform speed a railway wagon covers a distance of 49.5 km. in 2hrs 45 min. How long it will take to reach a station situated at a distance of 58.5 km?
Solution :
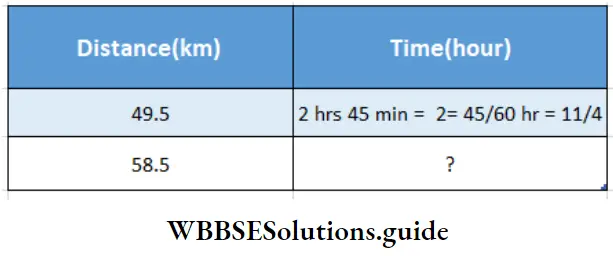
Given
Moving with a uniform speed a railway wagon covers a distance of 49.5 km. in 2hrs 45 min.
Distance & Time are in direct proportion
49.5 : 58.5 : : \(\frac{11}{4}\): ?
Time = \(\frac{58.5 \times \frac{11}{4}}{49.5}\)
= \(\frac{585}{495} \times \frac{11}{4}\)
= \(\frac{13}{4}\)
= 3 hr 15 min
∴ It will take 3 hr. 15 min. to reach the station
WB Class 7 Math Solution Question 9. My uncle went to Panchla on his motorbike, worked there for an hour, and returned home after 3hrs 30min. If he maintained a uniform speed of 40 km per hour, let us find the distance of Panchla from his home.
Solution :
Given
My uncle went to Panchla on his motorbike, worked there for an hour, and returned home after 3hrs 30min. If he maintained a uniform speed of 40 km per hour,
Total time taken 3 hrs 30 min but he worked there for 1 hr.
Total time for journey to go & return = 2 hr 30 min
= 2 \(\frac{1}{2}\) hr
= \(\frac{5}{2}\) hr
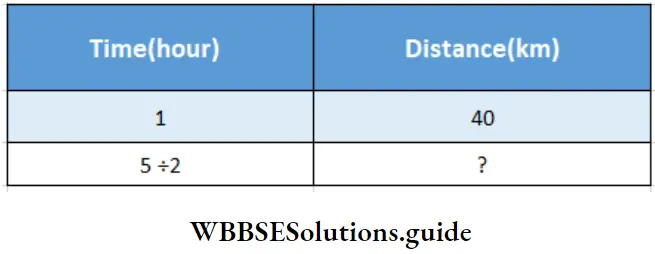
Time and Distance are in direct proportion,
1: \(\frac{5}{2}\) :: 40 ?
Distance = \(\frac{\frac{5}{2} \times 40}{1}\)
= 100
∴ 2 × distance to Panchla from his home = 100 km.
∴ Distance to Panchla from his home = \(\frac{100}{2}\)
= 50 km.
Distance to Panchla from his home = 50 km.
Question 10. A bus left Kolkata at 7:30 AM and without halting anywhere on its way reached Digha at 12 noon. If the uniform speed of the bus is 45 km/ hour, let us find the distance of Digha from Kolkata.
Solution :
Given
The bus left Kolkata at 7:30 AM & reached Digha at 1 2 noon.
Total time required to go Digha from Kolkata
= (12 Noon) -(7:30 AM) = 4 \(\frac{1}{2}\) hr
= \(\frac{9}{2}\) hr

1:\(\frac{9}{2}\):: 45?
∴ Distance = \(\frac{\frac{9}{2} \times 45}{1}\)
= \(\frac{405}{2}\) km
= 202. 5km
∴ Distance from Digha to Kokata = 202.5 km.
Question 11. A 70 m long train runs at a speed of 75 km/hr. Let us calculate how long it would take to pass a platform of length 105 metre.
Solution :
Given
A 70 m long train runs at a speed of 75 km/hr.
To pass a platform a train has to cover the length of platform + length of the train = (105 + 70) m = 175 m
Speed of the train = 75 km/hr.

∴ Distance & time are in direct proportion
75000: 175:: (60 × 60):?
Time = \(\frac{60 \times 60}{75000} \times 175\)
= \(\frac{42}{5}\) sec
= 8 \(\frac{2}{5}\)
∴ It would take 8 \(\frac{2}{5}\) sec. to pass the platform
WB Class 7 Math Solution Question 12. A 90 m long train takes 25 sec to pass a pole. Let me calculate the speed of the train in km/hr.
Solution :
Given
A 90 m long train takes 25 sec to pass a pole.
To pass the pole, a train has to cover its own length.
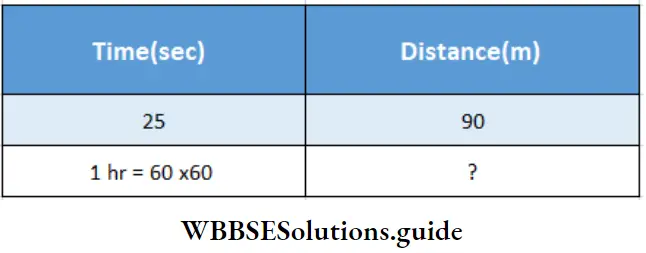
Time & Distance are in direct proportion.
25 :60 × 60 : : 90 : ?
∴ Distance = \(\frac{60 \times 60 \times 90}{25}\)m
= 12.96 km
∴ Speed of the train = 12.96 km/hr.
Question 13. To pass a bridge of length 250m a train of length 150m took 30 sec. Let’s calculate how long will this train take to pass a 130 m-long platform.
Solution:
Given
To pass a bridge of length 250m a train of length 150m took 30 sec.
Length of the train + length of the bridge
= (250 + 1 50) m = 400 m.
And length of platform + length of the train = (1 30 + 1 50) m = 280 m
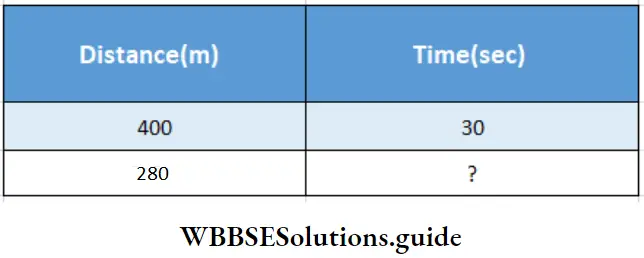
Time & distance are in direct proportion.
400 : 280: : 30:?
Time = \(\frac{280 \times 30}{400}\)
= 21 sec
∴ This train will take 21 sec. to pass the platform
Question 14. A passenger in a train found that the train took 15 sec to pass the platform. If the speed of the train is 60km per hour, let us find the length of the platform.
Solution :
Given
A passenger in a train found that the train took 15 sec to pass the platform. If the speed of the train is 60km per hour
Here the speed of the train = 60 km/hr. = 60000 m/hr. ,
The train took 15 sec to cross a platform

Distance = \(\frac{15 \times 60000}{60 \times 60}\)
∴ Length of the platform = 250 m.
Question 15. A train takes 4 sec to pass a telegraph post and 20 sec to pass a 264 m-long bridge. Let us find the length of the train and also its speed.
Solution :
Given
A train takes 4 sec to pass a telegraph post and 20 sec to pass a 264 m-long bridge.
In 20 sec the train covered its own length + the length of the bridge (264 m) & in 4 sec the train covered its own length (Subtracting) In 16 sec the train goes 264 m
In 4 sec the train goes \(\frac{264}{16} \times 4\) = 66m
Length of the train = 66 m.

4 : 3600 : : 6 : ?
Distance = \(\frac{3600 \times 66}{4} \mathrm{~m}\)
= \(\frac{3600 \times 66}{4 \times 1000}\) km
= 59.4 km
∴ Speed of the train = 59.4 km/hr.
WBBSE Class 7 Math Solution Question 16. A train passes two bridges of lengths 21 0m and 1 22m in 25 sec and 17 sec respectively. Let us calculate the length and speed of the train.
Solution :
Given
A train passes two bridges of lengths 21 0m and 1 22m in 25 sec and 17 sec respectively.
In 25 sec, the train covered its own length + a bridge of length 210m & in 17 sec, it covered its own. Length + a bridge of length 122m (Subtracting) we get in 8 sec, the train goes 88 m
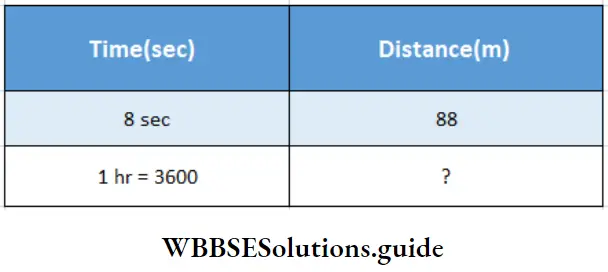
Time & distance are in direct proportion.
8 : 3600 : : 88 : ?
Distance = \(\frac{3600 \times 88}{8}\)
= 39600m
= 39.6 km
∴ Speed of the train = 39.6 km/hr.
Now again:

Time & distance are in direct proportion.
8: 15:: 88:?
Distance = \(\frac{25 \times 88}{8}\)
∴ Length of the train = (275- 210) m = 65 m
Question 17. A 100 m long train, remaining at a speed of 48 km/hr passes a tunnel in 21 sec. Let’s calculate the length of the tunnel.
Solution :
Given
A 100 m long train, remaining at a speed of 48 km/hr passes a tunnel in 21 sec.
Speed of the train = 48 km/hr
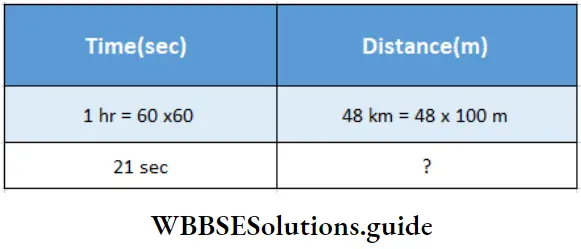
60 × 60:21 :: 48 × 1000:?
∴ Distance = \(\frac{21 \times 48 \times 1000}{60 \times 60}\) = 280 m
∴ Length of the tunnel = Total distance – Length of train
= (280 – 100)m = 180 m
Length of the tunnel = 180 m
Question 18. A train takes 1 0 sec to pass a man standing on the platform 1 50m long and passes the platform in 22 sec. Let us calculate the length and speed of the train.
Solution :
Given
A train takes 1 0 sec to pass a man standing on the platform 1 50m long and passes the platform in 22 sec.
In 22 sec. the train goes 150 m long platform + its own length
In 1 0 sec. the train goes its won length
(Subtracting) in 12 sec the train goes 150 m
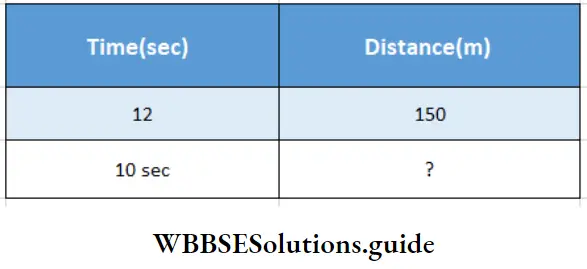
12: 10:: 150:?
∴ Distance = \(\frac{10 \times 150}{12}\)= 125 m/hr
∴ Length of the train = 125 m
Again to find speed:
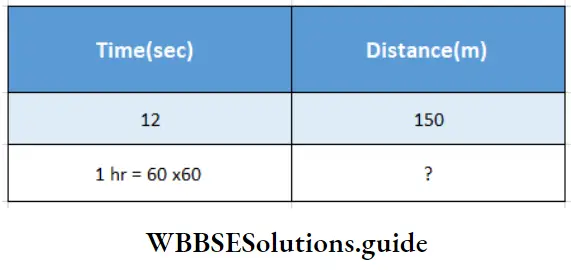
12 : (60×60) : : 150 : ?
∴ Distance = \(\frac{(60 \times 60) \times 150}{12}\) m/hr
= \(\frac{60 \times 5 \times 150}{1000}\) km
= 45 km
∴ Speed = 45 km/hr.
Question 19. Two trains of length 250 m and 200 m are approaching each other in two tracks side by side at speeds of 45 km/hr. and 36 km/hr. Let us find, after meeting each other, how long will they take to pass each other. [Let’s put numbers ourselves].
Solution :
Given
Two trains of length 250 m and 200 m are approaching each other in two tracks side by side at speeds of 45 km/hr. and 36 km/hr.

Total length of the two trains (250 + 200) m = 450 m.
Relative speed of the two train = (45 + 36) km/hr. = 81 km/hr
Time & distance are in direct proportion.
∴ (81 x 1000): 450:: 3600:?
∴ Required time = \(\frac{450 \times 3600}{81 \times 1000}\) = 20 sec
∴ They will take 20 sec to pass each other.
WBBSE Class 7 Math Solution Question 20. A goods train 250m long is running at a speed of 33 km/hr. Behind it another mail train 200m long and running at a speed of 60 km/hr. It is running in same direction on a different track & after meeting the goods train overpasses it. Let us find how long will the mail train take to overpass the goods train.
Solution :
Given
A goods train 250m long is running at a speed of 33 km/hr. Behind it another mail train 200m long and running at a speed of 60 km/hr. It is running in same direction on a different track & after meeting the goods train overpasses it.
Relative speed of the two train, when they are running in the same direction
= (60 – 33) = 27 km/hr.
Total distance covered by the mail train to over passes the other train
= (250 + 200) = 450 m.

Time & distance are in direct proportion.
∴ (27x 1 000): 450:: (60 × 60):?
∴ Time = \(\frac{450 \times 60 \times 60}{27 \times 1000}\)
= 60 sec
= 1 min
∴ The mail train will take 1 min. to overpass the goods train.
