WBBSE Solutions For Class 7 Maths Arithmetic Chapter 7 Areas Of Rectangles And Square Exercise 7 Solved Problems

WBBSE Class 7 Math Solution Chapter 7 Areas Of Rectangles And Square Exercise 7 Solved Problems

⇒ Surface: A surface is that plane figure which has only length and breadth, but no thickness.

⇒ Rectangle: A parallelogram is called a rectangle D whose each angle is right angle.

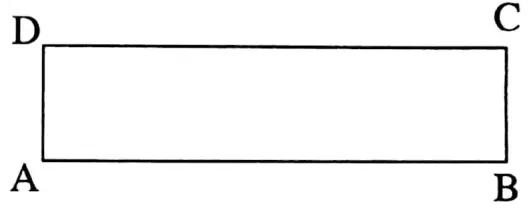
⇒ In a rectangle opposite sides are parallel and equal in length.

⇒ In rectangle ABCD, AB = DC, AD = BC and ∠A= ∠B =∠C = ∠D = 90°

Read and Learn More WBBSE Solutions for Class 7 Maths

⇒ The greater side of a rectangle is its length and the smaller side is its breadth or width. The length and breadth are known as the dimensions of the rectangle.

⇒ Square: A rectangle whose adjacent side are equal in length is called a square.

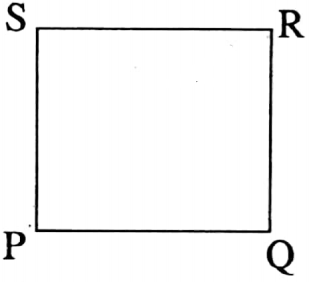
In square PQRS, PQ = QR = RS = SP and ∠P = ∠Q= ∠R = ∠S = 90°

⇒ Perimeter: The total length of the bounding lines of a figure is known as its perimeter. The perimeter is the sum of the lengths of its all sides. [semi-perimeter is the half of perimeter]

⇒ Area: Area is the measure of the quantity of surface occupied by a figure.

Some important formulas:

1. Perimeter of rectangle = 2 (length + breadth)
⇒ Semi-perimeter of rectangle = length + breadth
⇒ Area of rectangle = length x breadth

2. Perimeter of square = 4 x length of each side
⇒ Area of square = (length of side)²

3. Area of 4 walls of a room = perimeter x height
= 2 x (length + breadth) x height

Points to Note:

1. 1 Arc 100 sq. mt
2. 1 Sq. mt = 10000 sq. cm

Wbbse Class 7 Maths Solutions

Question 1. Choose the correct answer 

1. The perimeter of a square of side 3.5 cm is

1. 10-5 cm
2. 14 cm
3. 12-25
4. None of these

Solution: The perimeter of a square of side 3-5 cm is (4 x 3-5) cm are 14 cm

So the correct answer is 2. 14 cm

2. The area of a rectangle whose length is 18 cm and breadth is 15 cm is

1. 66 cm
2. 66 sq. cm
3. 270 cm
4. 270 sq cm

Solution: The area of a rectangle is (18 x 15) sq. cm = 270 sq. cm

So the correct answer is 4. 270 sq cm

3. If the area of a square is 12.25 sq. cm, then its perimeter is

1. 14 cm
2. 3.5 cm
3. 28 cm
4. 4.5 cm.

Solution: The area of square is 12.25 sq. cm

Let the length of each side of the square is x cm [x > 0]
∴ Area = x² sq. cm

According to the question:

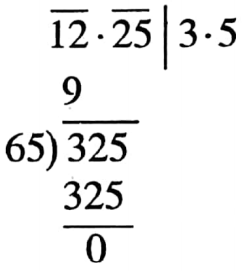
x² = 12.25

⇒ x=√12.25

⇒x= 3.5

∴ Length of each side of a square is 3.5 cm

Perimeter is (4 x 3.5) cm = 14.0 cm = 14 cm

So the correct answer is 1. 14 cm

Question 2. Write true or false

1. 1 Sq. km = 1000 Sq. m

Solution: 1 Sq. km = 1 km x 1 km

= 1000 m x 1000 m

= 1000000 sq.m

So the statement is false.

2. If the area of 3 cm square is 9 Sq. cm

Solution: Length of each side of a square is 3 cm

Area is (3 x 3) sq. cm = 9 sq. cm

So the statement is true.

3. If the length, breadth and height of a room is 8m, 6m and 5m respectively, then the area of its four wall is 140 sq. m.

Solution: Area of four walls of a room
= 2 (length + breadth) x height sq. unit
= 2 (8+6) x 5 sq. m
= 2 x 14 x 5 sq. m
= 140 sq. m

So the statement is true.

Question 3. Fill in the blanks

1. 1 Sq. m = _____ Sq. Hm.

Solution: 1 Sq. m = 1 m x 1m

= \(\frac{1}{100} \mathrm{Hm} \times \frac{1}{100} \mathrm{Hm}\)

= \(\frac{1}{10000}\) Sq. Hm

= 0.0001 Sq.cm

1 Sq. m = 0.0001 Sq.cm

2. 5 Sq. cm = _____ Sq.mm.

Solution: 5 Sq. cm = 5 cm x 1 cm

= 5 x 10 mm x 10 mm

= 500 sq. mm

5 Sq. cm = 500 sq. mm

Wbbse Class 7 Maths Solutions

3. The area of a square piece of land is 3600 sq. m. The cost of fencing all around the land at ₹ 4.50 per metre is ₹ _____

Solution:

Given

The area of a square piece of land is 3600 sq. m

∴ The length of each side = √3600 m

= 60 m.

Perimeter = (4 x 60) m = 240 m.

The cost of fencing all around the land at ₹4.50 per metre is ₹(240 x 4.50) or 1080.

Question 4. Distinguish between 5 metres square and 5 square metres.

Solution: 5 metres square means the area of the square each of whose sides is 5 metres.

So area of the square is 5 x 5 sq. m or 25 sq. m.

Again 5 Sq. m is meant the area of a rectangle or square the product of whose length and breadth is 5 sq. mt.

(such as 5 m x 1 m, 10m x 1/2 m etc).

Question 5. The length and breadth of a rectangular plot of land are 40 m and 30 m respectively. There is path 3 m wide running all around the plot outside. Calculate the area of the path.

Solution:

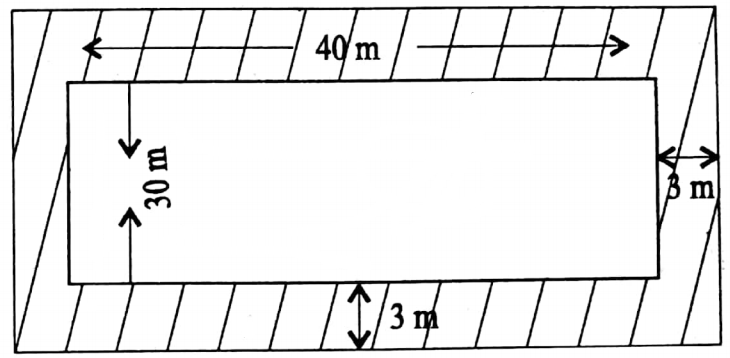
Given

⇒ The length and breadth of a rectangular plot of land are 40 m and 30 m respectively. There is path 3 m wide running all around the plot outside.

⇒ The area of the rectangular plot of land of length 40 m and breadth 30 m without path is (40 x 30) sq. m or 1200 sq. m.

⇒ The length of the plot of land including the path is (40+ 3 x 2) m or 46 m and that of breadth is (30+ 3 x 2) m or 36 m.

∴ The area of the plot of land including the path is (46 x 36) sq. m = 1656 sq. m.

∴  Area of the path is (1656-1200) sq. m = 456 sq. m.

Question 6. The length of the rectangular room is thrice of its breadth. The cost of varnishing the floor of the room at ₹ 7.50 per square metre is 810. Find the perimeter of the room.

Solution:

Given

The length of the rectangular room is thrice of its breadth. The cost of varnishing the floor of the room at ₹ 7.50 per square metre is 810.

Let the breadth of the room is x m.
∴ Length is 3x m.

Area of the floor is (3x x x) Sq. m = 3x² Sq.m.

The cost of varnishing the floor of the room at ₹ 7.50 per sq. m is ₹(3x² × 7.50)

According to question, 3x² x 7.50 =₹ 810

⇒ x² = \(\frac{810}{3 \times 7 \cdot 50}\)

⇒x=√36=6

∴ Breadth of the room is 6 m and length is (6 x 3) m or 18 m.

Perimeter is 2 (18 +6) m = 48 m.

Wbbse Class 7 Maths Solutions

Question 7. The cost of cultivation of a 25 m long piece of land in 150. If the breadth of the land be 10 m less, the cost would have been 75. Calculate the breadth of the land.

Solution:

Given

The cost of cultivation of a 25 m long piece of land in 150. If the breadth of the land be 10 m less, the cost would have been 75

Let the breadth of the land is x m.
Length of the land is 25 m.
Area of land is (25 x x) sq. m = 25 x sq. m

⇒ If the length of the land is 25 m and its breadth be (x 10)m. Then the area of land will be 25 (x-10)sq. m

⇒ The cost of cultivation of 25x sq. m land is ₹ 150

⇒ The cost of cultivation of 1 sq. m land is ₹  \(\frac{150}{25 x}\)

⇒ The cost of cultivation of 25(x-10) sq. m land is ₹ \(\frac{150 \times 25(x-10)}{25 x}\)

⇒ According to the question,

\(\frac{150(x-10)}{x}=75\)

⇒ 150×1500 = 75x
⇒ 150x75x = 1500
⇒ 75x = 1500

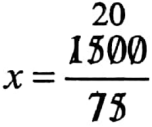
⇒ x= 20

∴ The breadth of the land is 20 m.

Question 8. The length and breadth of a rectangular hall is 24 m and 15 m respectively. Find how many square tiles of side 5 dcm

Solution:

Given

⇒ The length and breadth of a rectangular hall is 24 m and 15 m respectively.

⇒ The area of floor is (24 x 15) sq. m = 360 sq. m

⇒ Area of each square tiles is (5 x 5) sq. dcm = \(\frac{25}{100}\) sq.m

‎ ∴ Number of tiles is \(\left(360 \div \frac{25}{100}\right)\)

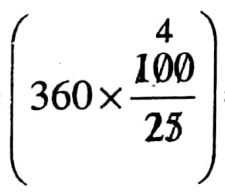
= 1440

Question 9. The length, breadth and height of a room of my school are 8 m, 6 m and 5 m respectively.

1. Find the cost of cementing the floor at ₹ 75 per square metre.
2. Find the cost of whitewashing its ceiling at ₹ 52 per sq. m..
3. The room has 2 doors each 1-5 m wide and 1.8 m high and has 2 windows each 1-2 m wide and 1-4 m high. Calculate the cost of painting doors and windows at ₹ 260 per square metre.
4. Also calculate the total cost of plastering the walls without doors and windows at ₹ 95 per sq m and cost of painting the walls at ₹ 40 per sq. m.

Solution:

Given

The length, breadth and height of a room of my school are 8 m, 6 m and 5 m respectively.

1. Area of the floor =(8 x 6) sq. m = 48 sq. m
∴ The cost of cementing the floor at ₹ 75 per sq. m is (48 x 75) = 3600

2. Area of ceiling = Area of floor = 48 sq. m
∴ The cost of whitewashing its ceiling at ₹ 52 per sq. m is ₹ 48 x 52 = ₹  2496

3. Area of 2 doors is (2 x 1.5 x 1·8) sq. m = 5.4 sq. m
⇒ Area of 2 windows is = (2 x 12 x 1.4) sq. m = 3.36 sq. m

⇒ Total areas of doors and windows is (5.4 + 3.36) sq. m = 8.76 sq. m

⇒ The cost of painting doors and windows at ₹ 260 per sq. m is ₹ 260 x 8.76 = ₹ 2277.60

4. Area of 4 walls is 2 (8 + 6) x 5 sq. m =

∴ Area of walls without doors and windows is (140 – 8.76) sq. m = 131.24 sq. m

⇒ Cost of plastering the walls without doors and windows at 95 per sq. m is ₹(131-24 × 95) = ₹ 12467-80

⇒ Cost of painting the walls at ₹ 40 per sq.m is ₹ (131-24 x 40) = ₹ 5249-60

∴ Total cost is ₹ (12467-80 + 5249-60) = ₹ 17717-40.

Wbbse Class 7 Maths Solutions

Question 10. If the area of the square is 110.25 sq. cm then find its perimeter.

Solution:

Given

⇒ Area of square = 110.25 sq. cm

⇒ Length of each side = √110.25 cm = 10.5 cm

⇒ Perimeter is (10.5 x 4) cm = 42.0 cm = 42 cm

Question 11.  In the adjacent length and breadth of a rectangular land are 50m and 40m respectively. The two paths with 2m wide and are parallel to length and breadth. Find the total area of the two paths.

 

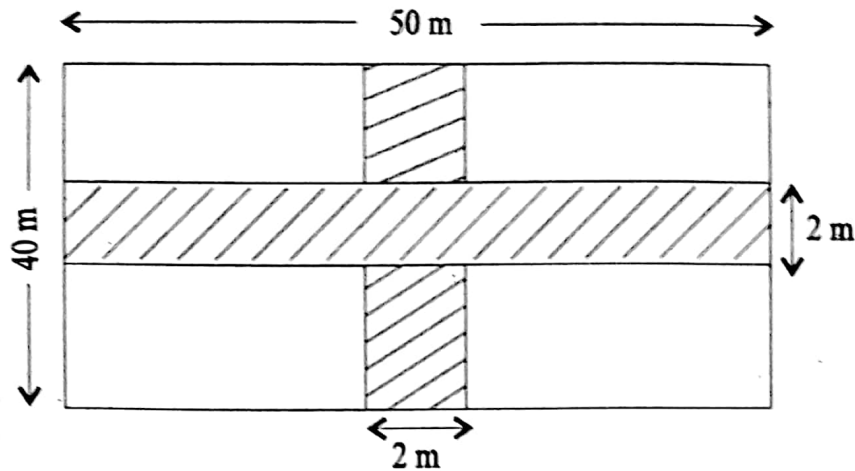
Solution:

Given

⇒ In the adjacent length and breadth of a rectangular land are 50m and 40m respectively. The two paths with 2m wide and are parallel to length and breadth.

⇒ The area of the path parallel to the length is (50 x 2) sq. m = 100 sq. m
⇒ The area of the path parallel to breadth is (40 x 2) sq. m = 80 sq. m

The area of common square region of side 2 m is (2 x 2) sq. m = 4 sq. m
∴ Total area of two paths is (100+ 804) sq. m = 176 sq. m

WBBSE Class 7 Math Solution Areas Of Rectangles And Squares

Areas Of Rectangles And Squares Exercise 7.1

Question 1. 1 sq. km. = (100 × 100) sq.
Solution:

1 sq. km. = (100 × 100) sq.Dm.

= 10000 sq.Dm.

1 sq. km. = 10000 sq.Dm.

Question 2. 1 sq. km. = (10 ×10) sq.Hm. = 1 00 sq.Hm.
Solution:  

1 sq. km. = (10 ×10) sq.Hm.

= 1 00 sq.Hm.

1 sq. km. = 1 00 sq.Hm.

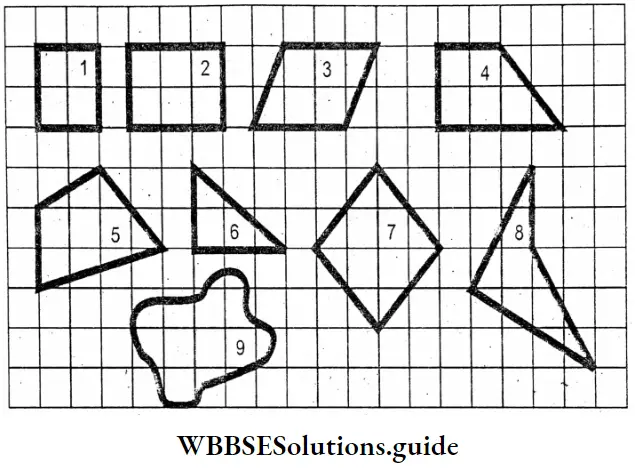
Question 3. In the graph has an area of [3] sq.cm, approximatily sq.m.
Solution:

= \(\frac{3}{100 \times 100}\)sq.m, approximately

= 3 × 10 × 10 = 300 sq. mm, approximately.

Question 4. Area of 6 in the graph = [8] sq. cm.
Solution :

Area of 6 = 8 sq. cm.

= \(\frac{8}{10000 \times 10000}\) = sqHm.

= 0.00000008 sq.Hm.

= 8 × 100 × 100 sq.mm. = 80000 sq.mm.

Question 5. Let us write the areas of Fig No. 7 and 8 in sq.cm. sq.Dm. & sq m.
Solution :

Area of 7 = 4 sq.cm.

= \(\frac{4}{1000 \times 1000}\) sq.Dm.

= 0.000004 sq.Dm.

= \(\frac{4}{100 \times 100}\)

= 0.0004 sq m.

Area of 8 = 6 sq.cm = \(\frac{6}{1000 \times 1000}\) sq.Dm.

= 0.000006 sq.Dm.

= \(\frac{6}{100 \times 100}\)= 0.0006 sq

Question 6. Let’s write the approximate value of areas of no 9 & 10 in ______ sq. cm _________ sq.cm.
Solution :

Area of  9 = 7 sq.cm. (Approx)

Area of 10 = 5 sq. cm. (Approx)

Class VII Math Solution WBBSE Areas Of Rectangles And Squares Exercise 7.2

Question 1. The height of the second new room of the village hospital is 7 m. Let us find the area of its 4,walls including doors and windows.
Solution :

Given

⇒ The height of the second new room of the village hospital is 7 m.

⇒ Length of the 2nd new room = 25 m

⇒ Breadth of the 2nd new room = 20 m

⇒ Height of the 2nd new room = 7m

∴ Area of 4 walls including doors & windows = 2 (L + B) x h

= 2 (25 + 20) × 7 sq m. = 630 sq m.

⇒ Area of 4 walls including doors & windows = 630 sq m.

Question 2. In the second room there are 2 doors of height 2 – 5 m. and 1 . 5 m. wide. Also, there are 2 windows which are 1 5 m. wide and 1 .8 m- high. Let’s calculate the cost of plastering its walls excluding the doors and windows at the rate of Rs. 75 per square meter.
Solution :

Given

⇒ In the second room there are 2 doors of height 2 – 5 m. and 1 . 5 m. wide. Also, there are 2 windows which are 1 5 m. wide and 1 .8 m- high.

⇒ Area of each door of the room

= 2 .5m. x 1.8 m. = 4.5sq m.

∴ Area of 2 doors of the room = 2 × 4. 50 sq m. = 9 sq m.

⇒ Area of each window of the room = 1.5m. × 1. 8 m. = 2.7 sq m.

∴ Area of 2 windows of the room = 2 × 2 . 7 sq m. = 5. 4 sq m.

Total area of 2 door & 2 window of the room

9.0 sqm. + 5.4 sqm. = 14. sqm.

∴ Total area of walls excluding 2 doors & 2 window

= (630 – 1 44) sqm = 6156 sq m.

∴ Cost of plastering wall excluding door & windows at the rate Rs. 75 per sq m.

= Rs. 6156 × 75.

= Rs. 46170.

Question 3. Let’s calculate the cost of painting the doors and windows of the second room at the rate of Rs. 300 per square meter.
Solution :

⇒ Total area of 2 doors & 2 windows = 2 × 45 + 2 × 27

= 9 + 54 = 144 sq m.

The cost of painting the doors & windows at the rate of Rs. 300 per sq m.

= Rs. 300 × 144 = Rs. 4320.

Question 4. Let’s calculate the cost of painting the ceiling with white color at the rate of Rs. 55 per square meter.
Solution:

⇒ Area of ceiling = L x B = 25m × 20m = 500 sq m.

⇒ The cost of painting the ceiling with white color at the rate Of Rs. 55 per sq m.

= Rs. 55 × 500 = Rs. 27,500.

Class VII Math Solution WBBSE Areas Of Rectangles And Squares Exercise 7.3

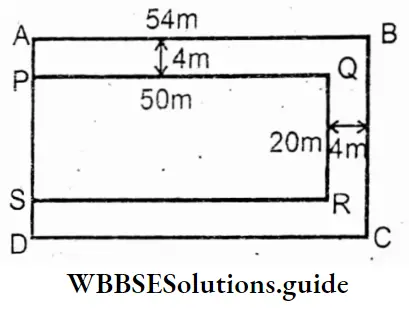
Question 1. ABCD is a rectangular plot of land. Let us find the area of a path 4m wide runs all around inside it, as seen in the figure.

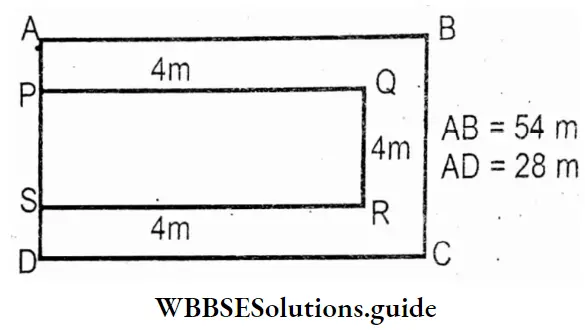
Solution:

Given

⇒ ABCD is a rectangular plot of land.

⇒ AB = 54m A B

⇒ AD = BC = 28m

∴ Area of ABCD = 54m × 28m = 1 51 2 sq m.

⇒ Again, PQ = AB – 4m = (54 – 4) = 50 m

QR = (28 – 4 – 4) = 20m _

∴ Area PQRS = 50 × 20 sq m. = 1000 sq m. D’

∴ Area of the path = Area of ABCD – Area of PQRS.

= 1512 sqm – 1000 sq m.

= 512 sq m.

⇒ Area of the path = 512 sq m.

Question  2. The area of a square park PQRS is 2500 sq m. and a path 6m wide runs all around outside the park. Let us find the area of this path.

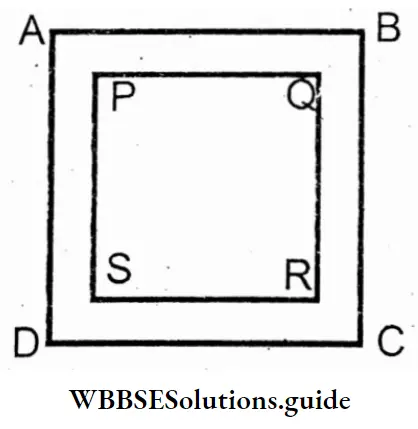
Solution:

Given

The area of a square park PQRS is 2500 sq m. and a path 6m wide runs all around outside the park.

Here the square PQRS = 2500 sq m. A

∴ PQ = V2500 = 50 m

∴  AB = PQ + 6m + 6m = (50 + 6 + 6) = 62m

∴ Area of ABCD = 62m × 62m = 3844 sq m.

∴  Area of PQRS = 2500 sq m.

∴  Area of the path = Area of ABCD – Area of PQRS

= 3844 sq m. – 2500 sq m.

= 1344 sq m.

Area of the path = 1344 sq m.

Areas Of Rectangles And Squares Exercise 7.4

Question 1. Let’s try to find out the area of the figure by counting the number of squares on graph paper

Solution:

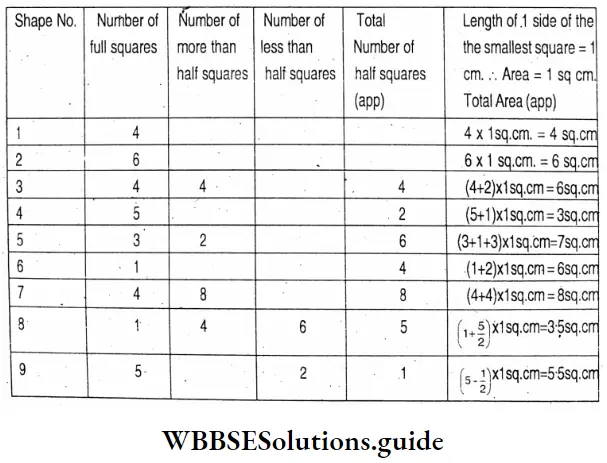
Question 2. Let us calculate mentally and write.

1. Let’s calculate the perimeter of a square of side 4 cm.
Solution:

⇒ Perimeter of a square of side 4 cm.

= 4 × 4cm = 16cm.

⇒ The perimeter of a square of side 4 cm = 16cm.

2. Let’s calculate the area of a square whose perimeter is 20 cm.
Solution :

⇒ The perimeter of a square = 20 cm.

⇒ Length of one side of the square = \(\frac{20}{4}\) = 5 cm

⇒ Area of the square of each side 5 cm = 5cm × 5cm

= 25 sq.cm.

⇒ The area of a square whose perimeter is 20 cm = 25 sq.cm.

3. Let us write the value of the area of a rectangle whose length is 8 cm. and breadth is 5cm.
Solution :

⇒ Length of the rectangle = 8cm

⇒ Breadth of the rectangle = 5cm

∴ Area of the rectangle = 8cm × 5cm

= 40 sq. cm.

Area of the rectangle = 40 sq. cm.

4. 1 sq km. =  ___________ sq Dm.
Solution :

1 sq km. = (100 × 100) sq Dm.

= 10000 sq Dm.

5. 1 sq km. = _____sq Hm. 
Solution:

1 sq km =  \(\left(\frac{1}{100} \times \frac{1}{100}\right)\)sq Hm.

= \(\frac{1}{10000}\)  sq Hm.

= 0.0001 sq Hm.

Class VII Math Solution WBBSE

6. Let us explain, what do 5 sq m. and 5 m. square mean.
Solution:

5 sq m. means an area of a field (any shape) = 5 sq m. but, 5m sq. means an area of a square whose each side = 5m.

∴ Area of that square = 5m × 5m = 25 sq m.

7. If the area of a square is 2 cm. square then the length of its side is [Hints: Area = 2cm. square = 2 cm × 2cm.]

The area of a square is 2cm. square, then the length of each side of the square

= 2cm & its area

= 2cm × 2cm = 4sq cm.

8. Let us draw a rectangle whose area is 30 sq cm. Let us find out what are its. possible lengths and breadths. Again, if the area of a rectangle is 40 sq cm. let us find its possible lengths and breadths.
Solution:

Area of a rectangle = 30 sq cm.

It’s length & breadth will be (10cm & 3cm), (15cm, 2cm), (6cm, 5cm) etc.

Area of a rectangle = 40 sq cm.

Then its possible length & breadth will be (2cm, 20cm); (4cm> 10cm)
(8cm, 5cm), (80cm, 0 5cm) etc.

9. Mihir made a square card of cardboard whose one side is 6 cm. let’s find the area of the card.
Solution:

One side of a square cardboard = 6cm.

Area of the cardboard = 6cm x 6cm = 36 sq cm.

10. The area of a 5m. square is _____________ sqm. [Let’s put the value]
Solution:

Area of a 5m. square = 5m × 5m = 25 sq m.

Question 3. On a rectangular piece of white paper,I draw two pictures as shown in the figure.

1. Let us find how much space of white paper the No. 1 picture is occupying.
Solution:

Area of white paper in No. 1 picture

= 8cm × 8cm = 64 sq.cm.

2. Let us find how much space of white paper picture the No. 2 is occupying.
Solution :

Area of white paperiri No. 2 picture

10cm × 6cm = 60 sq.cm.

Class VII Math Solution WBBSE

3. Let us calculate the area of white space is left in the white paper, after drawing the pictures (1) and (2).
Solution:

⇒ Total area of white paper = 32cm × 20cm = 640 sq.cm.

⇒ The total area of the two pictures = (64 + 60) sq. cm. = 12f sq. cm.

∴ Area of the white space left in the white paper after drawing the picture (1) & (2)

= 640 sq.cm – 124 sq.cm. = 516 sq.cm.

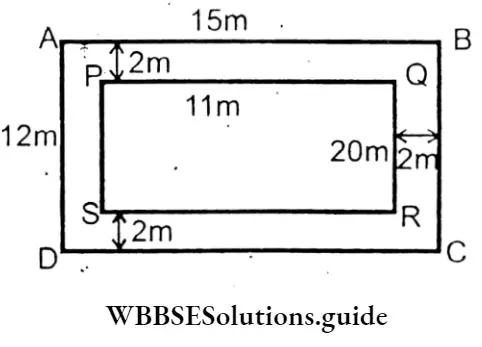
Question 4. The length and breadth of a page of my exercise book is 15 cm. and 12 cm. respectively. A margin of width 2 cm. is drawn on all sides, and wrote inside the margin. Let’s also draw a rough sketch for the problem. Let’s us find the area of the portion on which I wrote. Let’s also find the area of the portion on which I have not written.
Solution :

Given

The length and breadth of a page of my exercise book is 15 cm. and 12 cm. respectively. A margin of width 2 cm. is drawn on all sides, and wrote inside the margin.

Area of the paper ABCD= 15cm × 12 cm = 180 sq.cm.

Area of portion (Excluding margin) where I . will write

= 11cm × 8cm = 88sq.cm.

Area of the portion on which I have not written

= 180 sq.cm – 88 sq.cm.

= 92 sq.cm

Area of the portion on which I have not written = 92 sq.cm

Question 5. Rajesh has a rectangular plot of land of length 36m. and breadth 24m. There is a path 2m. wide running all around the plot outside. Let us draw a rough sketch of the problem and calculate the following 

1. Length and breadth of the plot of land including the path.
Solution :

Given

⇒ Rajesh has a rectangular plot of land of length 36m. and breadth 24m. There is a path 2m. wide running all around the plot outside.

⇒ Length of the field AB = 40m.

⇒ Breadth of Jhe field BC = 28m.

⇒ Area of the field ABCD = 40m × 28m = 1 1 20 sq m. (Ans.)

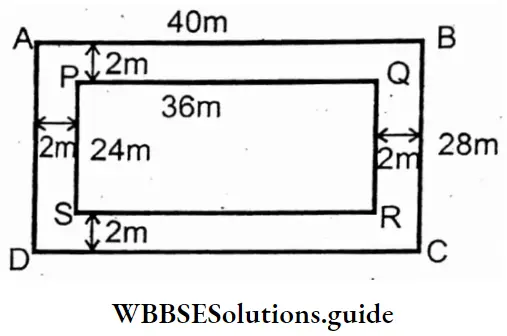
2. The area of the plot of land without the path.
Solution :

⇒ Length of the plot without a path (PQ) = 36m.

⇒ Breadth of the plot without a path (PS) = 24m

⇒ Area of the plot without path (PQRS) = 36m x 24m = 864 sq m.

3. Area of the path.
Solution:

Area of the path = Area of the plot ABCD – Area of the plot PQRS

= 1120 sq m. – 864 sq m.

= 256 sq m.

Area of the path. = 256 sq m.

Question 6. Maria’s family has a square plot of land of side 20m. A path 1m. wide runs ail around it from outside. Let’s find the area of the path.
Solution :

Given

⇒ Maria’s family has a square plot of land of side 20m. A path 1m. wide runs ail around it from outside.

⇒ Area of the square plot = 20m x 20m = 400 sq m.

⇒ Length of the plot with path = (20 + 1 + 1 )m = 22m.

⇒ Breadth of the plot with path = (20 + 1 + 1)m = 22m.

∴ Area of the plot with path = 22m × 22m = 484 sq m.

∴ Area of the path = 484 sq m – 400 sq m. = 84 sq m.

Question 7. The area of a square piece of land is 6400 sq m. Let’s find the cost of fencing all around the land at Rs. 3 50 per meter.
Solution:

Given

⇒ Area of square land – 6400 sq m.

⇒ Length of each side of the square land – 6400 m = 80 m.

⇒ The perimeter of the square land – 4 × 80m – 320m

⇒ The cost of fencing all around the land at Rs. 350/m = Rs. 350 × 320

= Rs. 1120.

Class VII Math Solution WBBSE

Question 8. The length of Karim’s uncle’s plot of land is twice its breadth and its area is 578 sq m. Let us find the length, breadth, and perimeter of Karim’s uncle’s land.
Solution:

Given

The length of Karim’s uncle’s plot of land is twice its breadth and its area is 578 sq m.

In this length of the land = 2 × breadth

∴ Area of the land = Length × breadth = (2 x breadth) x breadth

= 2 × (breadth)²

According to the problem

2 × (breadth)² = 578

(breadth)² = \(\frac{578}{2}\)

= 289

Breadth =  17m.

Length = 2 × 17m = 34m.

And perimeter of the land = 2 × (Length + Breadth)

= 2 × (34 + 17)m

= 2 × 51m = 102m.

perimeter of the land = 102m.

Question 9. The length of the rectangular stage of a theatre is twice its breadth. It costs Rs. 6048 to cover the whole stage with tarpaulin. If one sq m. of tarpanlin costs Rs. 21. Let’s find the length and breadth of the stage.
Solution:

Given

The length of the rectangular stage of a theatre is twice its breadth. It costs Rs. 6048 to cover the whole stage with tarpaulin. If one sq m. of tarpanlin costs Rs. 21.

Total cost to cover the whole stage (Area) with tarpaulin = Rs. 6048

Cost of 1 sq m. tarpanlin = \(\frac{\text { Rs. } 6048}{\text { Rs. } 21}\)

∴ Area of the stage = is 288 sq m.

∴  Length x breadth = 288

or, (2 x breadth) x breadth = 288

or, 2 x breadth² = 288

Area of the tarpaulin = = 288 sq m.

or, (breadth)² = \(\frac{288}{2}\) = 144

∴ Breadth = \(\sqrt{144}\) = 12 m.

∴ Length = 2 × breadth = 2 × 12m

= 24m.

Question 10. Nazreen will put Jari border on her sari of length 5 5m and breadth 1 25m. She decides to put a border of width 2 5 cm., along the breadth of the sari. Let’s find which portion of the sari will have Jari and which area of sari will be without Jari.
Solution :

Given

Nazreen will put Jari border on her sari of length 5 5m and breadth 1 25m. She decides to put a border of width 2 5 cm., along the breadth of the sari.

Area of the sari = 550cm x 125cm. = 68750 sq. cm.

Area of the sari excluding Jari = (550 – 1 0) x (1 25 – 5) = 540cm x 1 20cm

= 64800 sq. cm.

The area of sari will have Jari = (68750 – 64800)sq.cm.

= 3950 sq.cm. = 395 sq m

Now, length of the sari without Jari = (550 – 2 × 5)cm = 540cm.

Breadth of the sari without Jari = (1 .25 – 2 × 2-5)cm = 1 20 cm

Area of Sari without Jari = 540 cm × 120 cm = 64800 sq m.

= 6.48 sq m.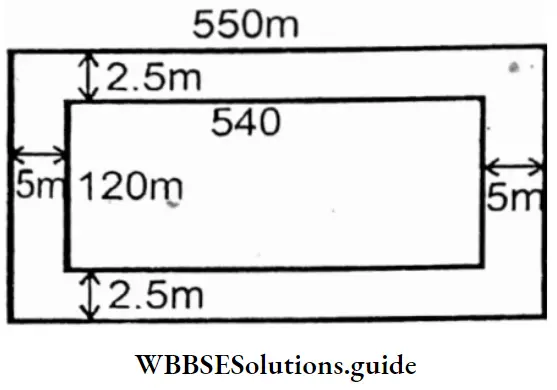

Question 11. As seen in the figure, two 5m. wide paths divide a rectangular garden into four equal parts. The length and breadth of the rectangular garden are 60m and 40m respectively. Let us calculate the cost of paving the path at Rs. 80 per square meter. Let’s also find the area of each part of the land. ‘
Solution :

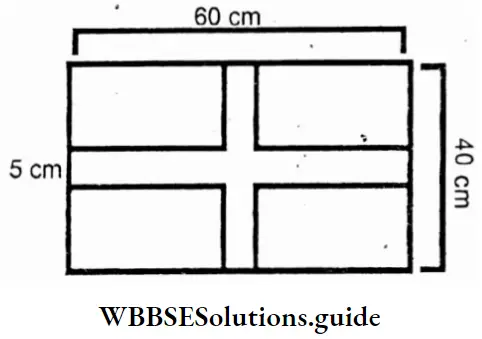
Given

As seen in the figure, two 5m. wide paths divide a rectangular garden into four equal parts. The length and breadth of the rectangular garden are 60m and 40m respectively.

Area of the garden = 60m  × 40m = 2400 sq m.

The area of the path along the length = 60m × 5m = 300 sq m.

Area of the path along the breadth = 40m × 5m = 200 sq m.

∴ The total area of the path = is 300 sq m. + 200 sq m. – (5m × 5m)

= 500 sq m. – 25 sq m.

= 475 sq m.

Cost of paving the path at the rare of Rs. 80/sq m.

= 475 x 80 = Rs. 38000

Area of the garden without path

= 2400 sq m. – 475 sq m. = 1925 sq m.

∴ Area of each part of the land = \(\frac{1925}{4}\) = 481 25sq m.

Question 12. The path that leads to our house is 2m wide. It divides our garden into two equal squares, as shown in the figure. The path is constructed for Rs. 8000 at the rate of Rs. 500 per sq m. Let us calculate the area of each square portion of garden. If the breadth of the whole plot of rectangular land on which the house is built is 4m, let us calculate the area occupied by the house itself.

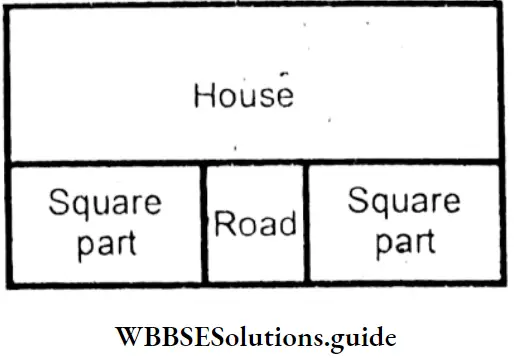
Solution :

Given

The path that leads to our house is 2m wide. It divides our garden into two equal squares, as shown in the figure. The path is constructed for Rs. 8000 at the rate of Rs. 500 per sq m.

Total construction cost = Rs. 8000.

At the rate of Rs. 500 per sq m.

∴ Area of the path = \(\frac{8000}{500}\) = 16 sq m.

Width of the path = 2m

∴ Length of the path = \(\frac{16}{2}\)  = 8m.

The area of each square portion of the garden

= 8m ×  8m = 64 sq m.

Length of the house = (8 + 2 + 8)m = 1 8m

Breadth of the house = 4m (given)

∴ Area of house = 18m × 4m = 72 sq m.

Class VII Math Solution WBBSE

Question 13. The cost of cultivation of a 30 m long piece of land is Rs. 150. If the breadth of the land be 5m less, the cost would have been Rs. 120. Let’s calculate the breadth of the land.
Solution :

Given

The cost of cultivation of a 30 m long piece of land is Rs. 150. If the breadth of the land be 5m less, the cost would have been Rs. 120.

Cost will be decreased by (Rs. 150 – Rs. 120) = Rs. 30

If the breadth decreased by 5m.

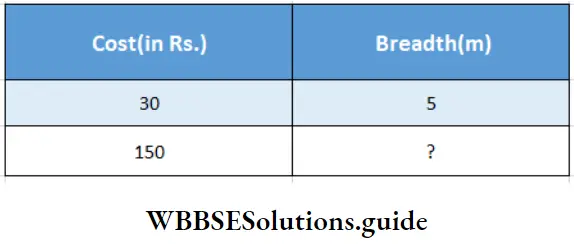
∴ 30 : 150 : 4 :: ?

∴ Breadth = \(\frac{150 \times 5}{30}\)

= 25 cm

The breadth of the land = 25 cm

Question 14. The length and breadth of a rectangular hall is 30m and 18m respectively. Let’s find how many square tiles of side 3 dcm. will be required for flooring the hall.
Solution :

Given

The length and breadth of a rectangular hall is 30m and 18m respectively.

Length of the hall = 30 m.= 300 dcm.

Breadth of the hall = 18 m = 180 dcm.

The area of each square tile = 3 dcm. x 3 dcm.

No. of tiles = \(\frac{300 \mathrm{dcm} \times 180 \mathrm{dcm}}{3 \mathrm{dcm} \times 3 \mathrm{dcm}}\)

= 100 × 60

= 6000

No. of tiles No. of tiles

Question 15. Jakir has a 18m x 14m rectangular plot of land. There is a square portion of garden of sides 3 4m. Let’s draw a rough sketch and calculate the area of the plot of land without the garden. Let’s also find how many square tiles of side 2 dcm. will be required to cover this vacant portion of land.
Solution :

Given

Jakir has a 18m x 14m rectangular plot of land. There is a square portion of garden of sides 3 4m. Let’s draw a rough sketch and calculate the area of the plot of land without the garden.

Area of Jakir’s rectangular plot of land

= 18m × 1 4m = 252 sq m.

Area of square portion of garden of sides 3 4m

= 34m × 34m = 1156 sq m.

Area of the plot of land without a garden

= (252 – 11 -56) sq m, = 24044 sq m.

Area of each square tile = 2 dcm × 2 dcm.

= 4 sq dcm. = 0 01 sq m. I_

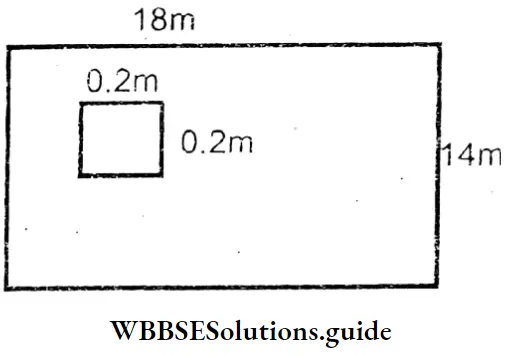
∴ No. of tiles required = \(\frac{240 \cdot 44}{0.04}\)

= 6011

Question 16. In the figures given below, let us find the areas of the colored portions

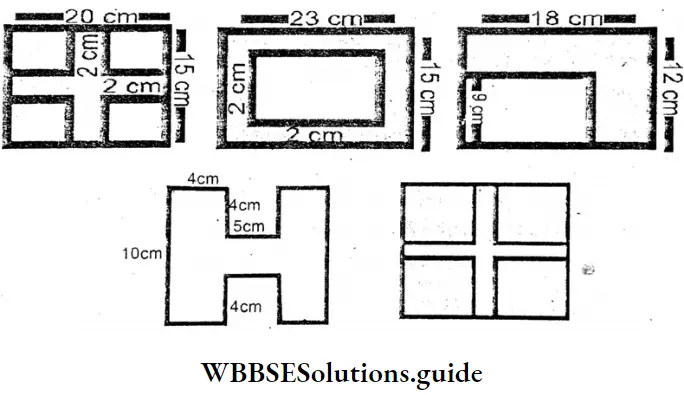
Question 17. Let us take the values of length and breadth on our own and find the area of the colored parts.
Solution:

In 1st figure:

The area of the colored portion

= (20cm × 2cm) + (1 5cm × 2cm) – (2cm × 2cm)

= 40 sq cm. + 30 sq cm. – 4 sq cm. = (70 – 4) sq cm.

= 66 sq. cm.

In 2nd figure:

The area of the colored portion

= (23cm × 15cm) – {(23 – 4) x (15 – 4)} sq cm.

= 345 sq cm. – (19cm × 11 cm)

= 345 sq cm. – 209 sq cm. = 136 sq cm.

In 3rd figure:

⇒ Area of the whole rectangle = 18m × 12m = 216 sq m.

⇒ Are of the write portion = 9m × (18 – 4)m. = 9m  × 14m

= 126 sq m.

⇒ Area of the coloured portion = 216 sq m. – 126 sq m. = 90 sq m.

In 4th figure:

⇒ Area of two vertical coloumn = (10cm × 4cm). ×  2 = 80 sq cm

⇒ Area of middle tile = 5cm × 2cm = 10 sq cm.

⇒ Total area of coloured portion = (80 + 10) sq cm. = 90 sq cm.

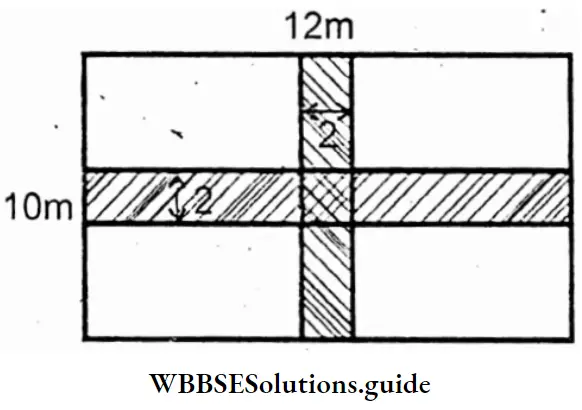
In the 5th figure let the length & breadth of the rectangles be 12m & 10m respectively & the width of the shaded portion = 2m

∴ Area of the shaded portion parallel to length = 12m × 2m = 24 sqm.

Area of the shaded porition parallel to breadth = 10m × 2m = 20 sqm.

∴  Area of the middle portion = 2m × 2m = 4sq m. .

∴  Total area of the shaded portion = 24 sq m + 20 sq m. – 4 sq m.

= 40 sq m.

Total area of the shaded portion = 40 sq m.

Question 18. The length, breadth and height of a room of my school are 8m, 6m and 5m respectively.

1. Find the cost of cementing the floor at Rs. 75 per square metre.
Solution :

Area of the floor = Length × breadth = 8m × 6m = 48 sq m.

Cost of cementing the floor at the rate of Rs. 75 sq m.

= Rs. 75 × 48

= Rs. 3600.

The cost of cementing the floor = Rs. 3600.

2. Let’s find the cost of whitewashing its ceiling at Rs. 52 per Sq m.
Solution :

Area of the ceiling = 8m x 6m = 48 sq m.

⇒ Cost of whitewashing its ceiling at the rate of Rs. 52/sq m.

= Rs. 52 × 48

= Rs. 2496.

⇒ The cost of whitewashing its ceiling = Rs. 2496.

Class VII Math Solution WBBSE

3. The room has 2 doors each 15 m wide and 18m high and has 2 windows each 12 m wide and 14 m high. Let’s calculate the cost of painting doors and windows at Rs. 260 per square metre,
Solution :

Given

⇒ The room has 2 doors each 15 m wide and 18m high and has 2 windows each 12 m wide and 14 m high.

⇒ Area of 2 doors = 2 × (1.8m  ×1.5m) = 2 × 27 sq m.

= 5.4 sq m.

⇒ Area of 2 windows = 2 x (1. 4m ×1.2m) = 2 ×1.68 sq m.

= 3 .36 sq m.

⇒ Total area of 2 doors and 2 windows

= 5.4 sq m + 3 .36 sq m. = 8 .76 sq m.

⇒ Cost of painting doors and windows at the rate of Rs 260/sq m.

= Rs 260 ×  8 .76 = Rs. 227760.

The cost of painting doors and windows = Rs. 227760.

4. Let’s also calculate the total cost ofplastering the walls, without doors and window at Rs. 95 per sq m and cost of painting the walls at Rs. 40 per sq m.
Solution :

⇒ Area of 4 walls of the room = 2 × (L + B) × H

= 2 × (8m + 6m) × 5m = 140 sq m.

⇒ Total area of 2 doors & 2 windows = 8 76 sq m.

⇒ Area of 4 walls without the area of doors & windows

= 140 sq m. – 876 sq m. = 131 -24 sq m.

⇒ Total cost of plastering and painting the walls

= Rs. 95 + Rs. 40 = Rs. 1 .35 per sq m.

⇒ Cost of plastering & painting of 131 24 sq m.

= Rs 1. 35 × 131 .24 = 1771740.

Question 19. Our local club room is square in shape of side 15m long, and 5m high. There are 4 doors in the club room each 15m wide and 2m high. Let’s calculate the cost of oil painting its 4 walls without doors at Rs. 350 per sq m.
Solution:

Given

⇒ Our local club room is square in shape of side 15m long, and 5m high. There are 4 doors in the club room each 15m wide and 2m high.

⇒ The area of 4 walls of the square room

= 2 × (L + L) × H = 2 × (15 + 15)m × 5m

= 300 sq m.

Area of 4 doors of the room

= 4 × 1.5m × 2m = 4 × 3 sq m. = 12 sq m.

Area of 4 walls without 4 doors

= (300 – 12) = 288 sqm.

Cost of oil painting = Rs. 350 per sq m.

∴  Total cost = Rs. 350 × 288 = Rs. 100800.

Question 20. Let’s draw a figure and calculate- within a rectangular plot of land, there is a square-shaped pond. There is a 3m wide paved path along its edge and on three sides of it, and on the other side there is an 18m broad garden. We calculated the area of the pond is ______________ sq m, the area of the path is _____________sq m.
Solution :

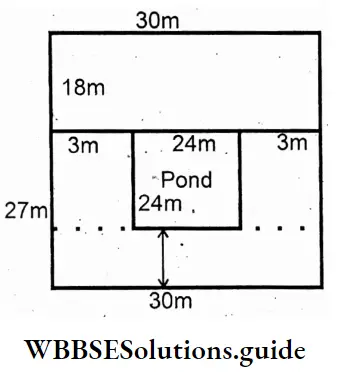
Let the length of the pond =.24m

∴ Area of the pond = 24m x 24m = 576 sq m.

Area of the path

= (30 × 3 + 24 × 3- 24 × 3) sq m.

= (90 + 72 + 72) sq m.

= 234 sq m.

Area of the path = 234 sq m.

Question 21. The length, breadth, and height of my rectangular room is _________ m, -_______ m and _________m. The areas of the 4 walls of my room including the doors and windows is ______________ sq m.
Solution :

⇒ The length of my room = (L) = 10m.

⇒ breadth of my room = (B) = 8m.

& Height of my room = (H) = 9m.

⇒ Area of 4 walls of my room = 2(L + B) × H

= 2(10 + 8) × 9 sq m.

= 324 sq m

Area of 4 walls of my room = 324 sq m