WBBSE Class 7 Math Solution Geometry Chapter 5 Concept Of Congruency Exercise 5 Solved Problems
⇒ If two geometrical figures are of the same shape and size, they are said to be congruent to each other.
⇒ Congruence is the property of two geometrical images if one of them can be made to coincide with the other by means of reflection, transformation, translation, rotation, or by their combination.
Read and Learn More WBBSE Solutions for Class 7 Maths
Congruence of the triangle:
⇒ Two triangles are said to be congruent if their respective sides, and angles are equal and when placed upon one another cover each other completely.
⇒ The congruence may be expressed by the symbol ‘≅’
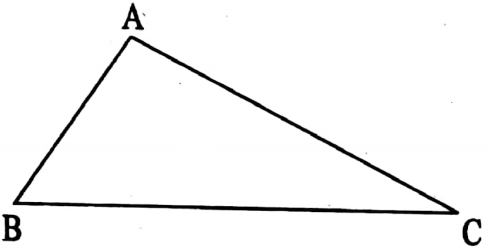
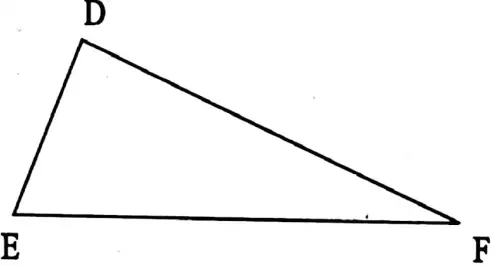
⇒ In two triangles ABC and DEF, if AB = DE, BC = EF, CA = FD and ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
∴ ΔABC≅ ≅DEF
The followings are the conditions for the congruency of triangles
1. SSS (Side-Side – Side)
2. SAS (Side-Angle – Side)
3. AAS (Angle – Angle – Side)
4. RHS (Right Angle – Hypotenuse – Side)
Wbbse Class 7 Maths Solutions
1. SSS: If the lengths of three sides of a triangle are equal to the lengths of three sides of the other triangle then the triangles are congruent.
⇒ In ΔABC and ΔDEF,
⇒ AB = DE, BC= EF and AC = DF
∴ ΔABC=ΔDEF
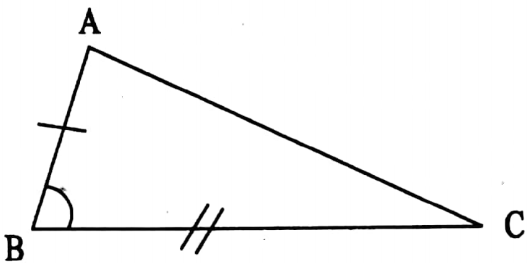
2. SAS: Two triangles are congruent if the length of two sides and the measurement of the included angle of one triangle are equal to the length of two sides and the measurement of the included angle of the other triangle.
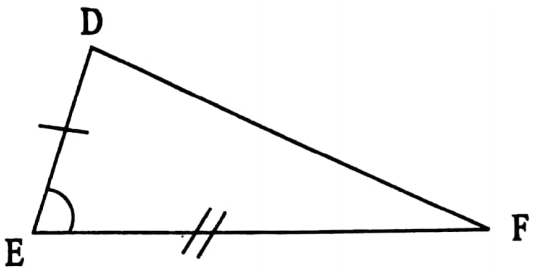
⇒ In ΔABC and ΔDEF,
⇒ AB = DE, ∠ABC = ∠DEF and BC= EF
∴ ΔABC ≅ ΔDEF
Wbbse Class 7 Maths Solutions
3. AAS: Two triangles are congruent if the measurement of any pair of angles and the length of one pair of corresponding sides are equal to the other triangle.
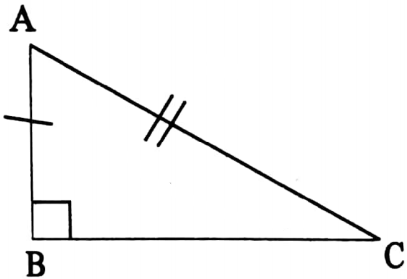
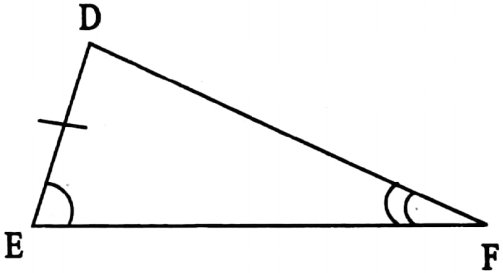
⇒ In ΔABC and ΔDEF,
⇒ ∠B = ∠E, ∠C = ∠F and AB = DE
∴ ΔABC ≅ ΔDEF
4. RHS: If in two right-angled triangles, the length of the hypotenuse and the length of one triangle is equal to the length of the hypotenuse and the length of one side of the other triangle, then the two triangles are congruent.
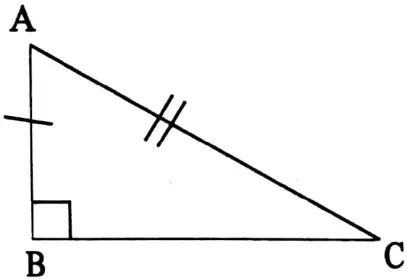
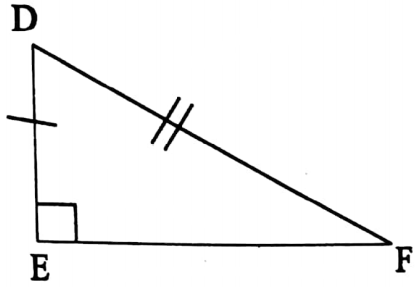
⇒ In ΔABC and ΔDEF,
⇒ ∠ABC = ∠DEF = 90°
⇒ hypotenuse AC = hypotenuse DF and AB = DE
∴ ΔABC ≅ ΔDEF
Wbbse Class 7 Maths Solutions
Similar triangle: If three angles of one triangle are equal to three angles of the other triangle then these two triangles are called similar triangles.
⇒ In ΔABC and ΔDEF,
⇒ ∠A = ∠D, ∠B = ∠E and ∠C = ∠F
⇒ but AB ≠ DE, BC ≠ EF and AC ≠ DF
∴ ΔABC and ΔDEF are similar triangles.
Two congruent triangles are always similar triangles but two similar triangles may not always be congruent.
Class 7 Math Solution WBBSE Concept Of Congruency Exercise 9
1. Let us write does congruency means.
Solution:
Congruency
⇒ Two shapes are said to be congruent if they have the exact same size and shape. One shape may be thought as of being an exact copy of a duplicate of the other.
⇒ Two triangles are congruent if all the angles and the sides in one triangle are exactly the same as the angles & sides of the other triangle.
2. Let’s write down the conditions of congruency of two triangles.
Solution:
There are four conditions of congruency of two triangles.
- If the lengths of three sides of a triangle is equal to the lengths of three
sides of the other triangle then the triangles are said to satisfy side – side – side or S – S – S condition. - If the measure of two sides and included angle of one triangle is equal to the measures of two sides and included angle of the two sides of that two side of the other, then the two triangles are said to satisfy side angle – side or S – A – S condition.
- If the measure of two angles and the side included between them of one triangle are equal to two angles and the corresponding side included between them of the other than the two triangles are said to satisfy angle – side angle or A – S – A condition.
- If the length of the hypotenuse and a side of a right-angled triangle is equal to the hypotenuse and a side of the other right-angled triangle, then the two right-angled triangles are said to satisfy Right angled – -hypotenuse – side ie. R – H – S condition or A – A – S condition.
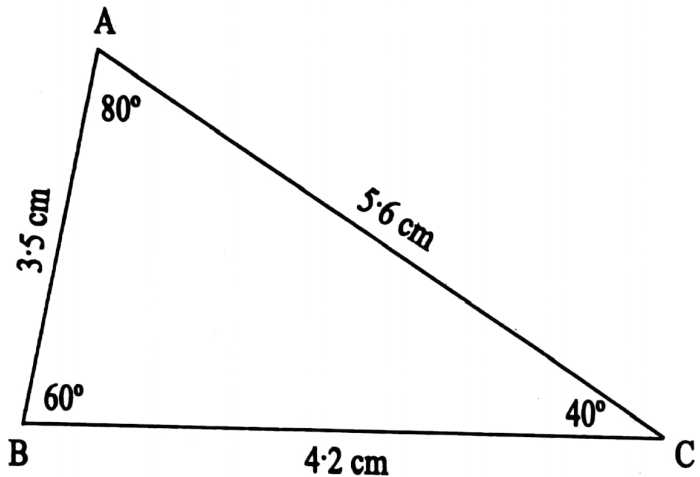
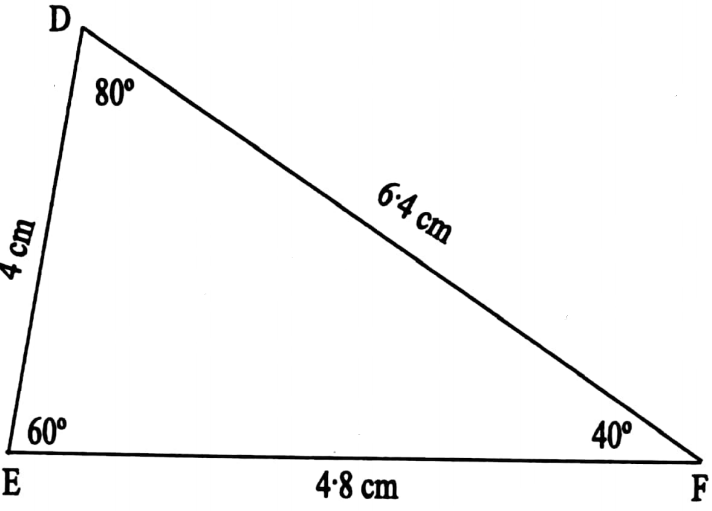
3. Let’s explain with a figure whether angle-angle-angle can be a condition for the congruency of two triangles.
Solution :
⇒ ABC and DEF are two equilateral triangles In Δ ABC, all the angles equal to go’ and each side = 4cm.
⇒ In Δ DEF each angle is equal to 60° but each side = 6cm, But it is clear from the two figures above that if Δ ABC, is cut off and placed or Δ DEF, they will not be coined.
∴ The triangles are not Congruent.
⇒ These types of triangles are called similar triangles.
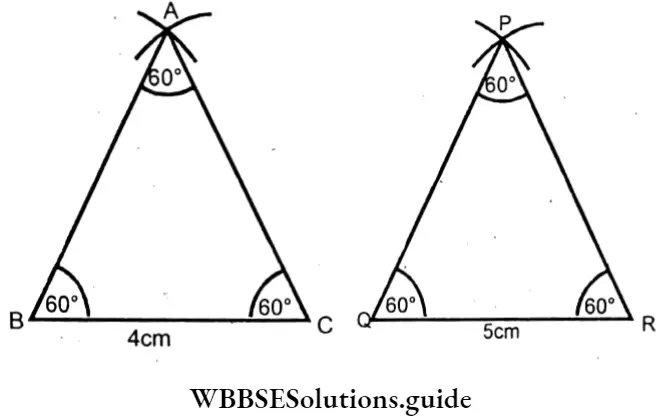
4. Let’s explain with conditions of congruency whether the following pair of triangles in all cases are congruent or not.
Solution :
⇒ Δ ABC & A PQR are two equilateral triangles each angle of both triangles is 60°
⇒ But each side of the 1st triangle is 4cm, whereas each side of the 2nd triangle is 5.5cm.
⇒ It is very clear from the figures above that if Δ ABC is cut off and placed on Δ PQR, they will not concede. That is the triangles are not congruent.
⇒ These triangles are called similar triangles.
5. Let’s explain with the condition of congruency whether the following pair of triangles in all cases are congruent or not.
1. Solution: These two triangles are congruent according to the S – S – S condition.
2. Solution: Δ PQR & Δ GHI are congruent according to the S – A – S condition.
3. Solution: Δ ABC & Δ DEF are congruent according to the S – A – S condition.
4. Solution: Δ ABC & Δ DEF are congruent according to the R – H – S condition.
5. Solution: Δ ABC & Δ DEF are not congruent.
6. Solution: Δ ABC & Δ DER. are congruent according to the A – S – A condition.
7. Solution: Δ ABC & Δ DEF are not congruent.
8. Solution: Δ ABC & Δ DEF are not congruent.