WBBSE Solutions For Class 8 Maths Chapter 16 Verification Of The Relation Between The Angles And The Sides Of A Triangle

Verification Of The Relation Between The Angles And The Sides Of A Triangle

Today Tania, Kuntal, Tulika and I have decided that we will try to make different types of shapes like triangle with different coloured straws and pins.

I formed by three straws-

The shape ABC is like a triangle. It has three sides AB,BC and three angles  and CA and three angles ∠BAC, ∠ABC and ∠ACB

l also formed a shape of a triangle like Tutika –

The exterior angle of ΔUVW is ∠UWX (∠UWX/∠UWV). In ΔUVW the interior opposite angles of the exterior angle ∠UWX are ∠UVW and ∠VUW

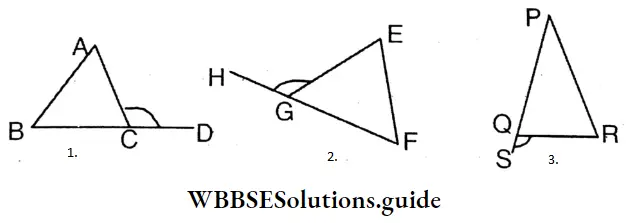
In figure1 the exterior angle is ∠ACD = 140 degree. So interior opposite angle ∠ABC = 50 degree and ∠BAC = 90 degree.

Now I will find the relation between the exterior angle and the interior opposite angle.

Read and Learn More WBBSE Solutions For Class 8 Maths

It is seen by measuring by a protractor, ∠ABC + ∠BAC= 140 degree = ∠ACD (approx).

My brother wrote by measuring three angles of each triangle by a protractor. In ΔABC the exterior angles are 90°, 50° and 40°; ∠ABC=50 degree, ∠BCA=40 degree, and ∠CAB=90 degree.

It is seen that ∠ABC + ∠BCA + ∠CAB =180 degree.

It is seen by measuring with a protractor, the sum of measurement of three angles of each triangle in figure 2 and 3 is 180 degree

4 Let’s cut off two angles ∠A and ∠B from another triangle and paste those two angles on the exterior angles of the first triangle as shown in the figure below :

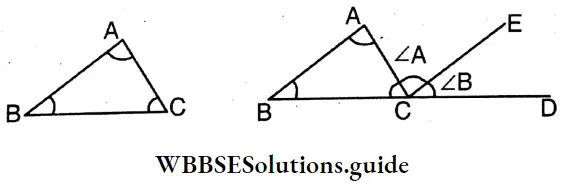
It is seen that the exterior angle ∠ACD = ∠A + ∠B = ∠BAC + ∠ABC

Theorem : We try to identify which postulates are required in the construction of the theorem. We also write which postulates are required for this theorem.

Tania drew triangle PUT and produced the side UT to R for this one exterior angle (∠PTR; and two interior opposite angles ∠PUT and  produced. Let’s prove logically step-by-step that ∠PTR= ∠PUT + ∠UPT.

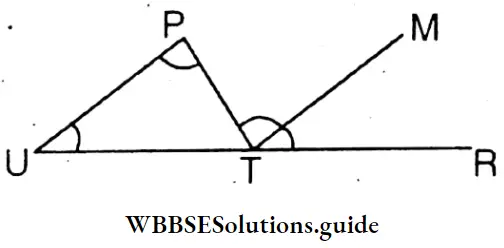
Given : PUT is a triangle whose side UT is extended to R. As a result an exterior angle ∠PTR and two opposite interior angles ∠PUT and ∠UPT are formed.

We have to prove that ∠PTR = ∠PUT + ∠UPT.

Construction : In ΔPUT from T parallel to UP a straight line TM is drawn.

Proof: UP//TM and UR is a transversal.

∴ ∠MTR = Corresponding ∠PUT

Again : UP//TM and PT is a transversal.

∴ ∠PTM = Alternate ∠UPT

∴ ∠MTR + ∠PTM = ∠PUT + ∠UPT

∴ ∠PTR = ∠PUT + ∠UPT Proved

The Sides Of A Triangle Exercise

Question 1. Let’s calculate and write the measurement of each of the exterior angles x° in each of the following triangles –

Solution:

The measurement of each of the exterior angles x° in each of the following triangles are

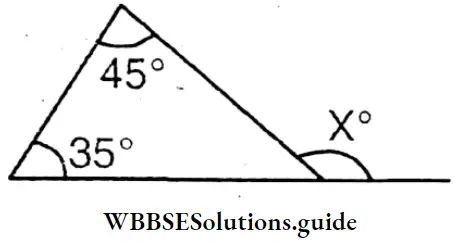
∠X = 35°+45°= 80°

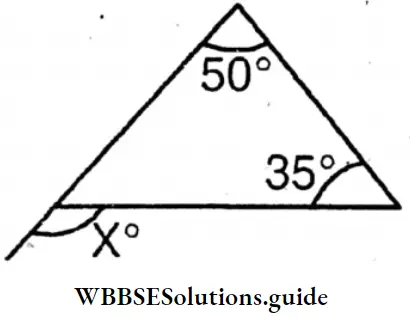
∠X = 50°+35°= 85°

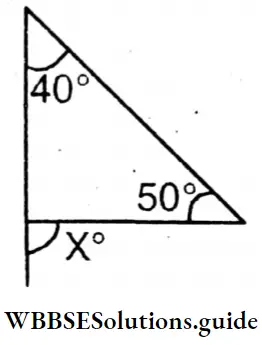
∠X = 50°+40°= 90°

Question 2. Let’s write the relation between the exterior angle ∠PRS and the interior opposite angles –

Solution:

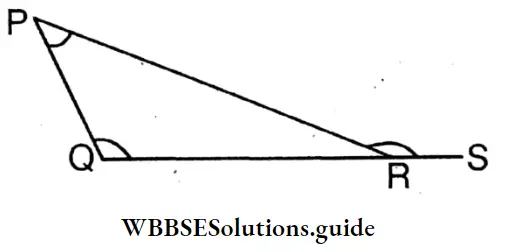
∠PRS = ∠PQR + ∠QPR

Pallabi and Kuntal drew some triangles of different shapes.

In is seen by measuring by a protractor that in ΔABC ∠BAC = 85 degree ∠ABC =60 degree and ∠ACB =35 degree. Again ∠BAC + ∠ABC + ∠ACB =180 degrees.

Kuntal measured with a protractor that in ΔACT ∠CAT = 145 degree ∠ACT = 20 degree and ∠CTA =15 degree. Again ∠ACT + ∠QAT + ∠CTA = 180 degree.

Pallabi measured and saw in ΔAMN that the sum of measurement of the three angles is =180 degrees.

The Sides Of A Triangle Exercise

I will find the value of missing angles from the triangles below.

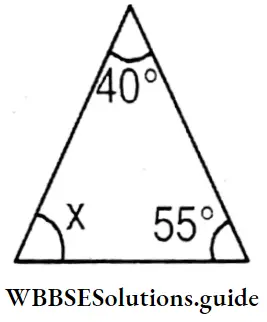
x = 180° – (40° + 55°)

= 180° – 95° = 85°

x = 85°

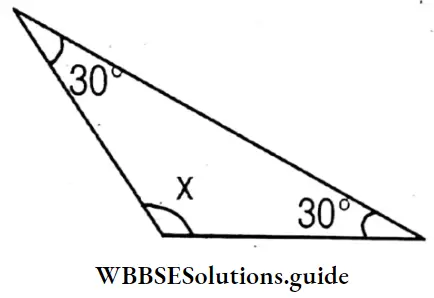
x = 180° – (30°+30°)

= 180° – 60° = 120°

x = 120°

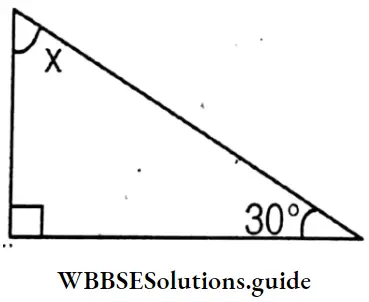
x = 180° – (30°+90°)

= 180° – 120° = 60°

x = 60°

The Sides Of A Triangle Exercise 16.3

Question 1. Find the value of ∠x in each of the following regions :

Solution:

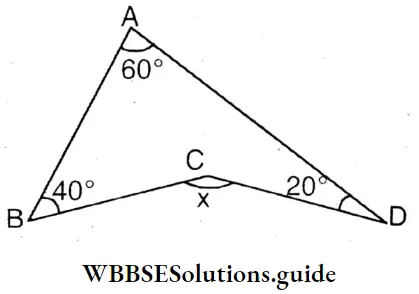
x = 60° + 40° + 20° =120

x =120

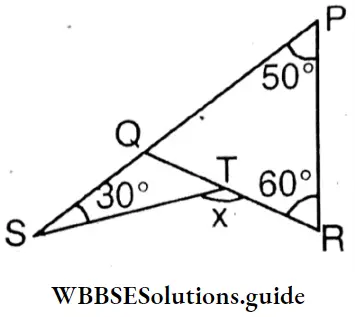
∠PQR = 180° – (50° + 60°) = 180° – 110° = 70

∴ ∠SQT = 180° -70° = 110°

∴ x = ∠SQT+ ∠QST =110° + 30°= 140°

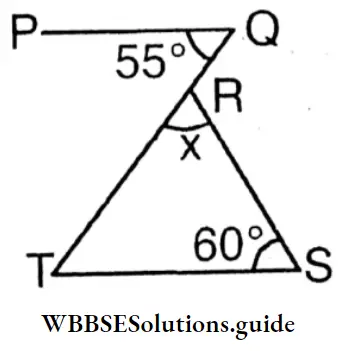
x = 180°-( ∠S+ ∠T) = 180° – (60°+55°) = 180°-115°= 65°

The value of ∠x = 65°

Question 2. From the figure beside find the value of the angles of ΔEHG.

Solution: 

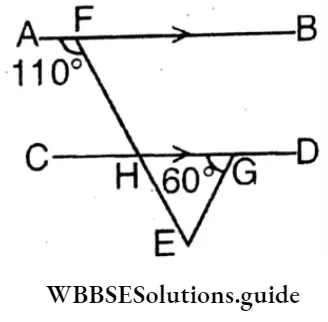
∠AFH = Corresponding ∠CHE = 110° (∵ AB//CD and EF is a transveral).

ΔEHG∠EHG = 180°- 110° = 70°

HGE = 60° (Given) and HEG = 180° – (70°+60°)

= 180° – 130° = 50°

The value of the angles of ΔEHG = 50°

Question 3. From the figure beside find the value of ∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F.

Solution:

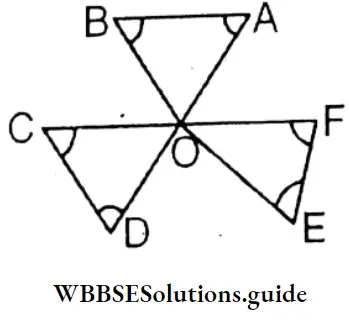
In ΔAOB ∠A+∠B+∠AOB=180° (1)

In ΔCOD ∠C+ ∠D+ ∠COD = 180° (2)

In ΔEOF ∠E + ∠F + ∠EOF-180° (3)

Adding (1), (2) and (3)

∠A + ∠B + ∠C + ∠D +∠E + ∠F + ∠AOB + ∠COD + ∠EOF = 540°

∵ ∠AOB = ∠DOE (∵ Vertically opposite angles)

∠COD = ∠AOF (∵ Vertically opposite angles)

and ∠EOF = ∠BOC (∵Vertically opposite angles)

∵ ∠AOB + ∠DOE + ∠COD + ∠AOF + ∠EOF + ∠BOC = 360°

∵ ∠AOB + ∠COD + ∠EOF = \(\frac{1}{2}\) × 360°= 180°

∵ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 540° – 180° = 360°

The value of ∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F = 360°

Question 4. If AB = AC then find the value of ∠ABC,∠ACB +∠ACD = 180°

Solution:

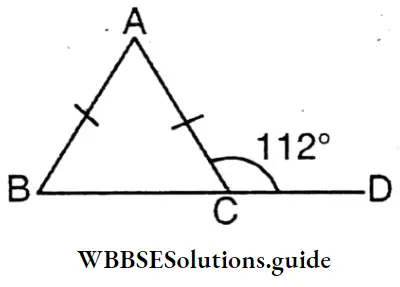
∠ACB +∠ACD = 180°

∴ ∠ACB + 112° = 180°

∴ ∠ACB =180° – 112° = 68°

∵ AB = AC

∴ ∠ACB = ∠ABC = 68°

∠BAC = 180° – (68° + 68°) = 180° – 136° = 44°

∴ ∠ABC = 68°,∠ACB = 68°, ∠BAC = 44°

The value of ∠ABC,∠ACB +∠ACD = 180°

Question 5. If AB = AC then find the value of ∠ABC and ∠ACB.

Solution:

In ΔABC ∠BAC = 80°

∠ABC + ∠ACB = 180° – 80° = 100°

∵ AB = AC

∴ ∠ABC = ∠ACB =\(\frac{100^{\circ}}{2}\) 50°

∴ ∠ABC = 50°, ∠ACB = 50°

Question 6. If AB = AC then find the value of ∠ACB and ∠BAC.

Solution:

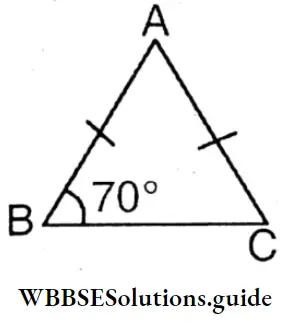
In ΔABC ∠ABC = 70c

∵ AB = AC

∠ABC = ∠ACB = 70°

∠BAC = 180° – (70° + 70°) = 180° – 140° = 40°

∴ ∠ACB = 70° and ∠BAC = 40°

Question 7. If AB = BC and ∠BAC + ∠ACB =50°; then find the value of the angles of ΔABC.

Solution:

∵ ∠BAC + ∠ACB = 50°

∵ AB = BC

∠BAC = ∠ACB = \(\frac{50^{\circ}}{2}\) = 25°

∴ ∠ABC = 180°-50°= 130°

If ΔABC ∠ABC = 130°, ∠BAC = 25°, ∠ACB = 25°

Question 9. If we produce the side BC on both sides, the two exterior angles are fomed. Let’s prove that the sum of the measurement of these two exterior angles is more than 2 right angles.

Solution:

Given: In ΔABC side BC is extended on both sides.

We have to prove that the sum of the exterior angles is more than 2 right angles, i.e., ∠ABD + ∠ACE > two right angles.

Proof : According to the relation between the exterior angle and the interior opposite angles, ∠ABD = ∠BAC + ∠ACB and ∠ACE = ∠BAC + ∠ABC

∴ ∠ABD + ∠ACE = ∠BAC + ∠ACB + ∠BAC + ∠ABC

∠ABD + ∠ACE = ∠BAC + ∠ACB + ∠ABC + ∠BAC

∠ABD + ∠ACE = 2 right angles + ∠BAC

(∵ The sum of all three angles of a triangle is equal to two right angles.)

∴ ∠ABD + ∠ACE > two right angles.

Question 9. Two straight lines parallel to sides BC and BA respectively through two vertices A and C of A ABC meet at D. Let’s prove that ∠ABC = ∠ADC.

Solution:

Given: Two straight lines parallel to sides BC and BA respectively through two vertices A and C of A ABC are drawn, which meet at D.

We have to prove that ∠ABC = ∠ADC.

Proof: In ΔABC and ΔADC

∠BAC = Alternate ∠ACD (∴ BA//CD and AC is a transversal)

∠ACB = Alternate. ZCAD (∴ BC//AD and AC is a transversal)

and AC is a common side.

∴ ΔABC = ΔADC(A-A-S)

∴ ∠ABC = ∠ADC Proved.

Question 10 .In ΔABC the internal bisectors of ∠ACB and ∠ACB angles meet at O. Let’s prove that ∠BOC = 90°-\(\frac{1}{2}\) ∠BAC.

Solution:

Given: In A ABC the internal bisectors of angles ∠ABC and ∠ACB meet at O.

Let’s prove that ∠BOC = ∠90° +\(-\frac{1}{2}\) ∠BAC.

Proof: In A ABC

∠A + ∠B + ∠C = 180°

∴ \(\frac{1}{2}\) ∠A + \(\frac{1}{2}\) ∠B + \(\frac{1}{2}\) ∠C × 180° = 90°

∴ \(\frac{1}{2}\) ∠B + \(\frac{1}{2}\) ∠C = 90° – \(\frac{1}{2}\) ∠A

Now, in ΔBOC

= \(\frac{1}{2}\) ∠B+ \(\frac{1}{2}\) ∠C + ∠BOC = 180°

∴  ∠BOC = 180° – (\(\frac{1}{2}\) ∠B+ \(\frac{1}{2}\) ∠C)

∴ ∠BOC=180°-(90°-\(\frac{1}{2}\) ∠A)

∴ ∠BOC = 180° – 90° + \(\frac{1}{2}\) ∠A = 90° + \(\frac{1}{2}\) ∠A Proved

Question 11. In A ABC the external bisectors of ∠ABC and ∠ABC meet at O. Let’s prove that ∠BOC = 90° \(-\frac{1}{2}\) ∠BAC.

Solution:

Given

In ΔABC the external bisectors of ∠ABC and ∠ACB meet at O.

We have to prove that ∠BOC = 90° – \(\frac{1}{2}\)∠BAC.

Proof: ∵ ∠ABC + ∠OBC + ∠OBP = 180°

or, ∠ABC + ∠OBC + ∠OBC = 180° (∵ ∠OBC = ∠OBP)

or, ∠ABC + 2 ∠OBC = 180°

or, 2 ∠OBC = 180°- ∠ABC

or, ∠OBC = 90° –\(\frac{1}{2}\) ∠ABC

Similarly, ∠OCB = 90°-\(\frac{1}{2}\) ∠ACB

Now, in ΔBOC,

∠OBC + ∠OCB + ∠BOC = 180°

or, 90° – \(\frac{1}{2}\) ∠ABC + 90° – \(\frac{1}{2}\) ∠ACB + ∠BOC = 180°

or, 180° – \(\frac{1}{2}\) (∠ABC + ∠ACB) + ∠BOC = 180°

or, ∠BOC = \(\frac{1}{2}\) (∠ABC + ∠ACB)

or, ∠BOC = \(\frac{1}{2}\)(180°- ∠BAC) (∵ ∠A+ ∠B + ∠C = 180°)

∴ ∠B + ∠C = 180° -∠A

or, ∠BOC = 90°\(\frac{1}{2}\) ∠BAC Proved.

Question 12. One base angle of the isosceles triangle ABC is twice of the vertical angle. Let’s write the measurement of the three angles of the triangle.

Solution:

Given

One base angle of the isosceles triangle ABC is twice of the vertical angle.

Let ABC is a triangle where AB = AC and ∠B = 2 ∠A

∵ In ΔABC, AB = AC

∴ ∠B= ∠C

Let ∠A = X

∴ ∠B= ∠C = 2X

Proof: In ΔABC,

∠A + ∠B + ∠C = 180°

or, X + 2X + 2X = 180°

or, 5X = 180°

or X = \(\frac{180^{\circ}}{5}\)

or, X = 36°

∴ ∠A = X = 36°

∴ ∠B = ∠C = 2 x 36° = 72°

∴ The angles of the triangle are 36°, 72°, 72°

Question 13. In ΔABC, ∠BAC = 90° and ∠BCA = 30°. Let’s prove that AB: \(\frac{1}{2}\) BC.

Solution:

Given

In ΔABC, ∠BAC = 90° and ∠BCA = 30

Let’s prove that AB = \(\frac{1}{2}\) BC.

Proof: In A ABC

∠ABC = 180° – (90° + 30°) = 180° – 120° = 60°

∵ ∠C= 30° and ∠B= 60° ,

∴ ∠B = 2∠C

∵ The opposite side is proportional to the angles of a triangle. The opposite side of ZC is AB and the opposite side of ∠B is AC.

∵ The opposite side of the largest angle is the largest and that of the smallest angle is the smallest. Here the value of ∠B is double than that of ∠C.

∴ AB = \(\frac{1}{2}\) AC Proved.

Question 14. In ΔXYZ, ∠XYZ = 90° and XY=XZ. Let’s prove that ∠YXZ = 60°

Solution:

Given : ∠XYZ = 90° and XY = XZ

Here ∠Y is the largest.

∴ XZ is the largest side

∴ XY≠XZ The question is fallacious.

Question 15. Let’s prove that the measurement of-each angle of an equilateral triangle is 60°.

Solution:

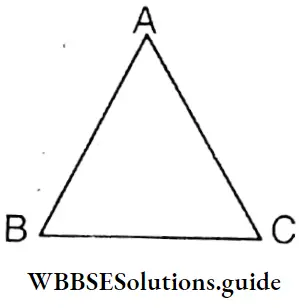
Let ABC is a triangle where AB = BC = AC.

Let’s prove that ∠A = ∠B = ∠C = 60°.

Proof : The sides of a triangle are proportional to the angles.

∵ AB = BC = AC

∴ ∠A = ∠B = ∠C

∵ The sum of the three angles of a triangle is 180°.

∴ ∠A + ∠B + ∠C = 180°

or, ∠A + ∠A + ∠A = 180°

or, 3∠A = 180°

or, ∠A =\(\frac{180^{\circ}}{3}\) = 60°

∴ ∠A = ∠B = ∠C = 60° Proved.

Question 16. The bisector of ∠BAC of ΔABC and the straight line through the mid point D of the side AC and parallel to the side AB meet at a point E, outside BC. Let’s prove that ∠AEC = 1 right angle.

Solution:

Given

The bisector of ∠BAC of ΔABC and the straight line through the mid point D of the side AC and parallel to the side AB meet at a point E, outside BC.

Diptarka and Puja have made different triangles of different shapes and colours. Any two sides of these triangles are unequal. They formed-

I measure the length of each side of each triangle and let’s compare which side is smaller and which one is greater.

Measuring we see, in ΔABC, the length of AC > the length of AB.

In ΔPQR, the length of PR > the length of QR.

In ΔXYZ, the length of XZ > the length of XY

Now, let’s measure each angle triangle with a protractor and compare.

Measuring we see, in ΔABC ∠ACB [>] ∠ACB [ Put</> ]

In ΔPQR, ∠PQR [>] ∠QPR [ Put</> ]

In ΔXYZ, ∠XYZ > ∠YZX ∠YXZ /∠YZX Put ]

But it is seen that in ΔABC, AC is opposite to the side ∠ABC and AB is opposite to the side ∠ACB.

Again, in ΔPQR, opposite angle to the side PR is ∠PQR and the opposite angle to the side QR is ∠QPR

And, in ΔXYZ, opposite angle to the side XZ is ∠XYZ and the opposite angle to the side XY is ∠XYZ

Measuring with a protractor I got the measurement of the angle opposite to the greater side of each triangle than the angle opposite to the smaller side is greater [greater/smaller]. Pallabi and Sirap drew some triangles whose any two sides are unequal.

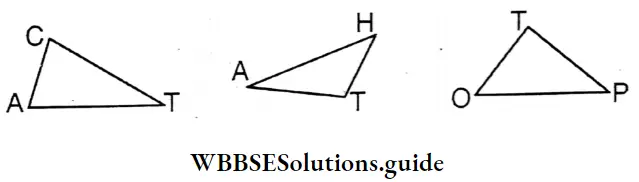
Measuring the sides of the triangle with a scale and the angles of the triangle with a protractor we see that the measurement of the angle opposite to the greater side is greater (smaller/greater) than the measurement of the angle opposite to the smaller side .

The Sides Of A Triangle Exercise

Question 1. Let’s measure the length of the sides of the following triangles and let’s compare the angles :

Solution:

1. ∠P>∠R(∠R/∠Q)
2. ∠X>∠Z(∠Y/∠Z)
3. ∠C>∠B(∠A/∠B)

Pallabi and Siraj drew some triangles, each of whose two angles are unequal.

Now I measure the angles with a protractor and let’s compare the angles of each triangles.

Measuring I see, in ΔMAN, ∠AMN > ∠MAN [</>Put]

In ΔPAN, ∠PAN > ∠PNA [∠PNA / ∠APN Put ]

In ΔFAN, ZFNA < FAN [ ∠FAN / ZAFN Put ]

Let’s measure each side of each triangle with a scale and let’s compare the length of the sides.

Measuring I see, in ΔMAN, MN < AN [ >/< Put ]

In ΔPAN, PN > PA [ PA / AN Put ]

In ΔFAN, AN < FN [ FA / FN Put ]

But it is seen that in ΔMAN the opposite side of ∠AMN is AN

and the opposite side of ∠MAN is MN

In ΔPAN the opposite side of ∠PAN is PN

and the opposite side of ∠PNA is AP

In ΔFAN the opposite side of ∠FNA is FA

and the opposite side of ∠FAN is FN

I got by measuring with a scale and a protractor that in each triangle the length of the side opposite is to greater side than the length of the side opposite |greater| (greater/smaller).

The Sides Of A Triangle Exercise

Question 1. Let’s observe the angles of the following triangles and let’s compare the length of the sides which one is smaller and which one is greater:

Solution:

Side BC > side AB [Put >/<]

Side YZ > side XY [Put XZ/XY]

Side PR > side PQ [Put up side]

The Sides Of A Triangle Exercise 16.6

Question 1. In figure ∠QPR > ∠PQR. Let’s write the relation between PR and QR.

Solution:

Given ∠QPP > ∠PQR

The opposite side of ∠QPR is QR and the opposite side of ∠PQR is PR.

∵  The side of the largest angle of a triangle is greater than that of the smallest angle.

∴ QR>PR

Question 2. In ΔABC, AC>AB. D is any point on the side AC such that ∠AOB = ∠ABD. Prove that ∠ABC > ∠ACB.

Solution:

Given

In ΔABC, AC > AB; D is any point on the side AC such that ∠ADB = ∠ABD.

Prove that ∠ABC > ∠ACB.

Proof : ∠ADB = ∠DBC + ∠BCD (∵ The exterior angle of A BCD is ZADB)

or, ∠ABD = ∠DBC + ∠BCD (∵ ∠ADB = ∠ABD)

or, ∠ABD = ∠DBC + ∠ACB (∵ ∠BCD and ∠ACB are the same angle)

Again, ∠ABC = ∠ABD + ∠ACB

Question 3. In triangle ABC, AD is perpendicular to BC and AD, BC, AC > AB. Let’s prove that :

Solution:

1. ZCAD > ZBAD
2. DC > BD.

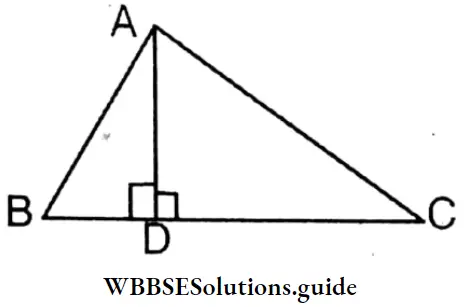
Given

In ΔABC, AD is perpendicular to BC and AC > AB.

Prove that: 1. ∠CAD > ∠BAD; 2.  DC > BD.

Proof: In Δ ∠ABC ∠BAC + ∠ABC + ∠ACB = 180°

In ΔADC ∠DAC + ∠ADC +∠ACD = 180°

or, ∠DAC + 90° + ∠ACD = 180° [∵ AD⊥C]

or, ∠DAC + ∠ACD = 180° – 90° = 90°

In ΔABD ∠BAD + ∠ABD + ∠ADB = 180°

or, ∠BAD + ∠ABD + 90° = 180° [∵ AD⊥C]

or, ∠BAD + ∠ABD = 180° – 90° = 90°

∴  ∠BAD +∠ABD = ∠DAC + ∠ACD = 90°

∵ AC > AB

∴  ∠B > ∠C

∴ ∠CAD > ∠BAD

(1) (Proved)

∴ In ΔABD ∠D= 90° and ∠A + ∠B = 90°, ∠B> ∠A

∴ AD > BD

Similarly in ΔADC, DC > AD

∴ DC > AD > BD

∴ BD > BD (ii) (Proved)

Question 4. In figure AB < OB and CD > OD. Let’s prove that ∠BAO > ∠OCD.

Solution:

Given

AB < OB and CD > OD

Prove that ∠BAO > ∠OCD

Proof : ∵ CD > OD

∴  ∠COD >∠OCD

and ∠COD = ∠BOA (Vertically opposite angles)

Again, AB < ∠OB

∠BOA < ∠BAO

or, ∠COD < ∠BAO (∵ ∠BOA = ∠COD)

In triangle OCD, ∠COD > ∠OCD (∵ CD > OD)

and ∠BAO > ∠COD –

∴ ∠BAO > ∠OCD (Proved)