WBBSE Class IX Maths Solutions WBBSE Chapter 1 Real Numbers
Definitions :
- Natural Numbers: The numbers from which objects are counted, are called natural numbers. Eg: 1, 2, 3, 4….., etc.
- Whole Numbers: In the group of natural nos. by adding 0 (zero), the new group of numbers so formed, is called a group of whole nos. Eg. 0, 1, 2, 3, etc.
- Integers: The group of negative numbers, zero, and natural numbers is called Integers. Eg: -4, -3, -2, -1, 0, 1, 2, 3, 4……….., etc. the numbers on the left side of zero are called negative integers and the numbers on the right side of zero are called positive integers.
- Even Numbers: Those whole numbers which are completely divisible by 2 are called even numbers. Eg. 2, 4, 6, 8, etc. The digit on the units place of these numbers is any of 0, 2, 4, 6, and 8. Eg: 482, 940, etc.
- Odd Numbers: Those whole numbers which are completely divisible by 2, are called Odd Numbers. Eg: 1,3, 5, 7, 9, etc.
- Prime Numbers: Those natural nos. which are divisibly only by 1 (one) and themselves, and are not divisible by any other numbers, are called prime numbers. Eg: 2, 3, 5, 7, 11., etc.
- Composite Numbers: Those natural numbers which are divisible except 1 and themselves by at least one number, are called composite Numbers. Eg: 4, 6, 8, 9, 10…, etc.
- Rational Numbers: If any number can be divided in the ratio of two whole numbers, i.e., in the form of \(\frac{p}{q}\) where p and q are whole numbers and q≠0 then that number is called (Rational number) Eg. \(\frac{3}{8}, \frac{2}{3}, 10, \frac{-3}{5}\) are rational numbers.
- Irrational number: Those numbers which cannot be expressed as the ratio of two whole numbers, are called Irrational numbers. Eg. \(\sqrt{5}, \sqrt[3]{7}, \sqrt[4]{21}\) etc.
Class 9 Math Chapter 3 WBBSE
Read and Learn More WBBSE Solutions For Class 9 Maths
Class 9 Mathematics West Bengal Board Chapter 1 Real Numbers Excercise 1.1
Question 1. Let us write the definition of rational numbers and also write 4 rational numbers.
Solution: Any number of the form \(\frac{p}{q}\) where p and q are in integers and q≠0, is called a rational number. All integers and fractions are rational numbers.
4 rational numbers are \(\frac{2}{3}, \frac{17}{5}, \frac{-1}{2}, \frac{-5}{1}\) (i.e., -5).
Question 2. Is 0 a rational number? Let us express 0 in the form of \(\frac{p}{q}\) [Where p & q are integers and q ≠0 and p & q have no common factor other than 1].
Solution: Yes, as \(0=\frac{0}{1}\)
Question 3. Let me place the following rational numbers on the Number Line:
Solution:
1. 7
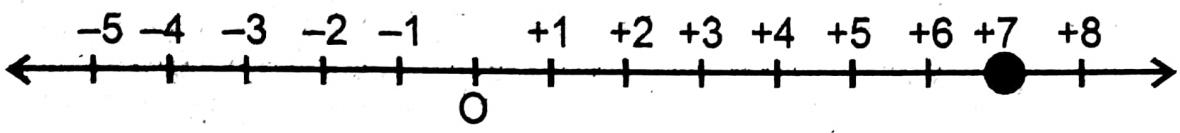
2. -4
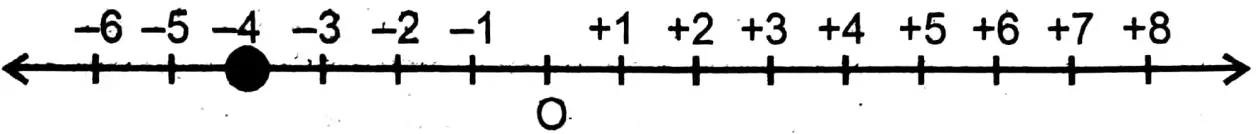
3. \(\frac{3}{5}\)
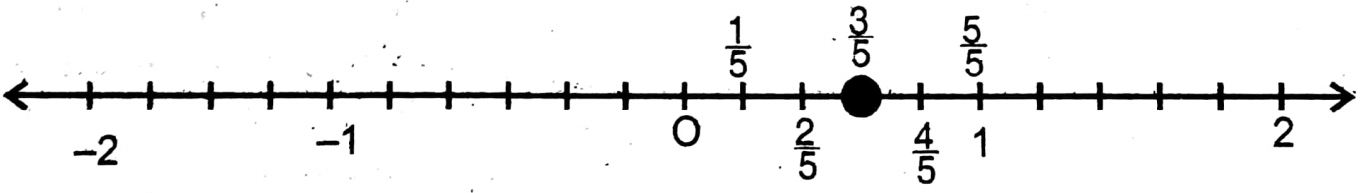
4. \(\frac{9}{2}\)

5. \(\frac{2}{9}\)

Wbbse class 9 maths chapter 1 real numbers solutions
6. \(\frac{11}{5}\)

7. \(-\frac{13}{4}\)
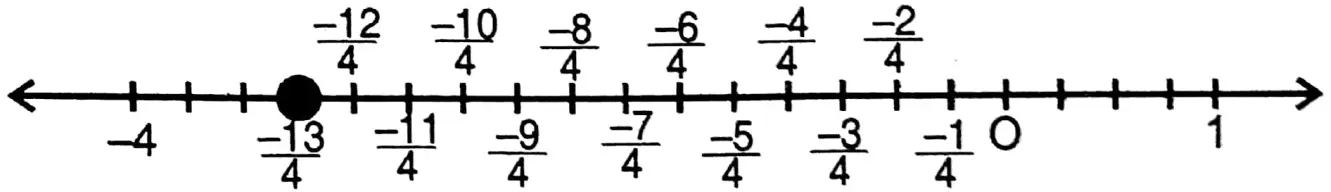

wbbse class 9 maths real numbers chapter 1 exercise solutions
Question 4. Let me write one rational number lying between two numbers given below and place them on the Number Line:
1. 4 and 5
Solution: \(\frac{4+5}{2}=\frac{9}{2}\)

2. 1 and 2
Solution: \(\frac{2+1}{2}=\frac{3}{2}\)

3. \(\frac{1}{4} \text { and } \frac{1}{2}\)
Solution: \(\frac{\frac{1}{2}+\frac{1}{4}}{2}=\frac{3}{8}\)

WBBSE Class 9 Math Chapter 3.2
4. \(-1 \text { and } \frac{1}{2}\)
Solution: \(\frac{(-1)+\frac{1}{2}}{2}=-\frac{1}{4}\)
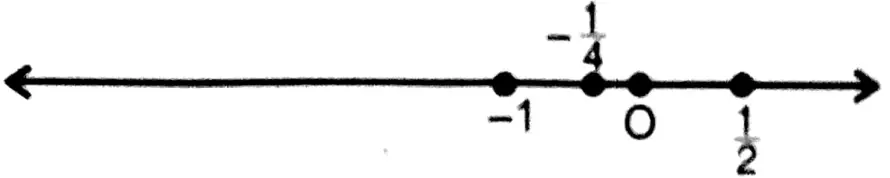
class 9 wbbse maths chapter 1 real numbers solved questions
5. \(\frac{1}{4} \text { and } \frac{1}{3}\)
Solution: \(\frac{\frac{1}{4}+\frac{1}{3}}{2}=\frac{7}{24}\)
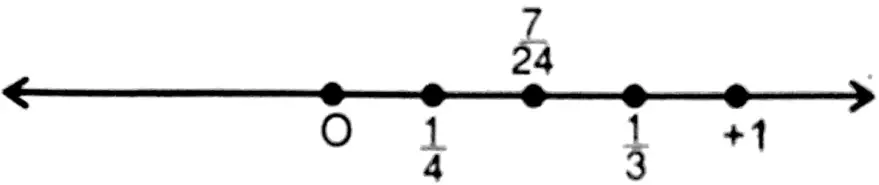
6. -2 and -1
Solution: \(\frac{(-2)+(-1)}{2}=\frac{-3}{2}\)

Question 5. Let me write 3 rational numbers lying between 4 and 5 and place them on the Number Line.
Solution:\(\frac{1}{2}(4+5)=\frac{9}{2}, \frac{1}{2}\left(4+\frac{9}{2}\right)=\frac{17}{4}, \frac{1}{2}\left(5+\frac{9}{2}\right)=\frac{19}{4}\)
∴ 4 and 5 in between 3 rational numbers: \(\frac{17}{4}, \frac{9}{2}, \frac{19}{4}\)

Question 6. Let me write 6 rational numbers lying between 1 & 2 and place them on the Number Line.
Solution: Here x = 1, y = 2 and n = 6.
∴ \(\mathrm{d}=\frac{2-1}{6+1}=\frac{1}{7}\left(therefore \mathrm{d}=\frac{\mathrm{y}-\mathrm{x}}{\mathrm{n}+1}\right)\)
∴ 6 rational numbers are (x + d), (x + 2d), (x + 3d), (x + 4d), (x + 5d) and (x + 6d),
i.e., \(\left(1+\frac{1}{7}\right),\left(1+\frac{2}{7}\right),\left(1+\frac{3}{7}\right),\left(1+\frac{4}{7}\right),\left(1+\frac{5}{7}\right),\left(1+\frac{6}{7}\right)\)
WBBSE Class 9 Math Chapter 3.2
∴ \(\frac{8}{7}, \frac{9}{7}, \frac{10}{7}, \frac{11}{7}, \frac{12}{7}, \frac{13}{7}\) rational numbers lie between 1 and 2.

wbbse 9th class maths chapter 1 real numbers step by step guide
Question 7. Let me write 3 rational numbers lying between \(\frac{1}{5} \text { and } \frac{1}{4}\).
Solution: Here x = \(\frac{1}{5}\), y = \(\frac{1}{4}\) and n = 3.
∴ d=\(\frac{\frac{1}{4}-\frac{1}{5}}{3+1}=\frac{\frac{1}{20}}{4}=\frac{1}{20} \times \frac{1}{4}=\frac{1}{80}\)
∴ 3 rational numbers = (x + d), (x + 2d), (x + 3d)
\(\begin{aligned}& =\left(\frac{1}{5}+\frac{1}{80}\right),\left(\frac{1}{5}+\frac{2}{80}\right),\left(\frac{1}{5}+\frac{3}{80}\right) \\
& =\frac{17}{80}, \frac{18}{80}, \frac{19}{80} \\
& =\frac{17}{80}, \frac{9}{40}, \frac{19}{80}
\end{aligned}\)
Class IX Maths Solutions WBBSE

Question 8. Let me put (T) if the statement is true and write (F) if the statement is wrong.
- By adding, subtracting, and multiplying two integers, we get integers.
Solution: True - By dividing two integers, we get an integer.
Answer: False
Question 9. Let me see and write what I will get by adding, subtracting, multiplying, and dividing (divisor is non-zero) two rational numbers.
Answer: Rational number:
Let two rational numbers be \(\frac{7}{10} \& \frac{19}{30}\)
By adding, \(\frac{7}{10}+\frac{19}{30}=\frac{21+19}{30}=\frac{40}{30}=\frac{4}{3}\)
By subtracting, \(\frac{7}{10}-\frac{19}{30}=\frac{21-19}{30}=\frac{2}{30}=\frac{1}{15}\)
By multiplying, \(\frac{7}{10} \times \frac{19}{30}=\frac{133}{300}\)
By dividing, \(\frac{7}{10} \div \frac{19}{30}=\frac{7}{10} \times \frac{30}{19}=\frac{7 \times 3}{1 \times 19}=\frac{21}{19}\)
∴ By adding, subtracting, multiplying, and dividing two rational numbers we will get the rational numbers.
Class IX Maths Solutions WBBSE
Class 9 Maths WB Board Chapter 1 Real Numbers Exercise 1.2
Question 1. Let us write the right or false statement from the following:
- The sum of two rational numbers will always be rational.
Solution:(True) - The sum of two irrational numbers will always be irrational.
Solution:(False) - The product of two rational numbers will always be rational.
Solution:(True) - The product of two irrational numbers will always be rational.
Solution:(False) - Each rational number must be real.
Solution:(True) - Each real number must be irrational.
Solution:(False)
wbbse class 9 real numbers chapter 1 important questions
Question 2. What is meant by irrational numbers? – Let me understand. Let me write 4 irrational numbers.
Solution:
Irrational Number: Irrational Numbers are numbers which can not be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q ≠ 0, i.e., a number √a (square root of a) is an irrational number if a is positive and a is not the square of a rational number.
Examples: √2: √3: √5: \(\sqrt{7 / 3}\)(all positive irrational numbers)
\(-\sqrt{3} ;-\frac{\sqrt{3}}{4}\) (Negative irrational numbers)
Class 9 Maths Chapter 1 WBBSE
Question 3. Let us write rational and irrational numbers from the following:
- √9
- √225
- √7
- √50
- 100
- -√81
- √42
- √29
- -√1000
Solution:
Rational Numbers:
1. √9
2. √225
4. √100
6. -√81
Irrational Numbers:
3. √7
4. √50
6. √42
7. √29
8. -√1000
Question 4. Let me place √5 on the Number Line.
Solution:
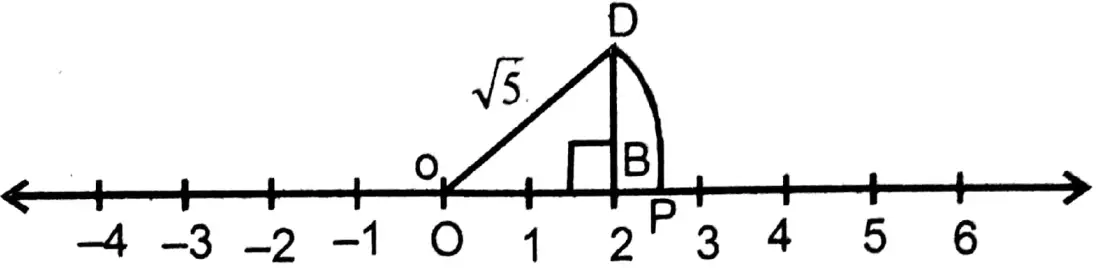
On the number line, take OB = 2 unit & DB (on OB) = 1 unit.
∴ OD= \(\sqrt{2^2+1^2}\)=√5. With center O & radius OD an arc is drawn, which intersects the number line at P.
∴ OP = √5 unit.
Question 5. Let me place √3 on the Number Line.
Solution:
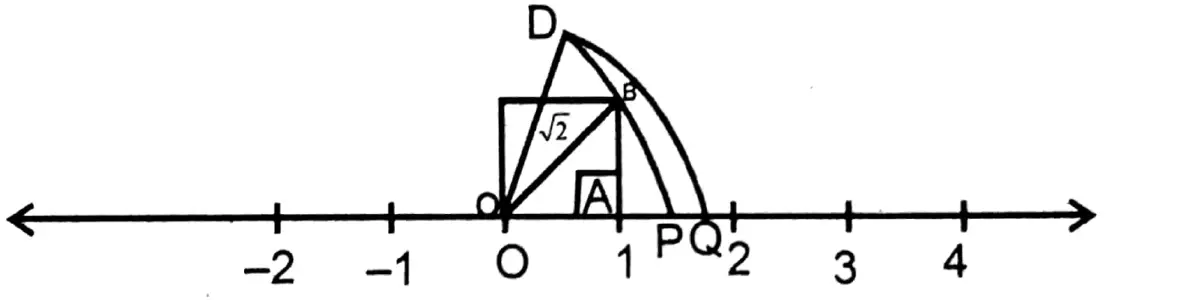
\(\begin{aligned}
& O D=\sqrt{(O B)^2+(B D)^2} \\
& =\sqrt{(\sqrt{2})^2+(1)^2} \\
& =\sqrt{2+1}=\sqrt{3}
\end{aligned}\)
Class 9 Maths Chapter 1 WBBSE
With center O & radius OD an arc is drawn which intersects the number line at Q. OQ=√3 unit.
Question 6. Let me place √5, √6, √7,-√6,-√8,-√11 on the Number Line.
Solution:
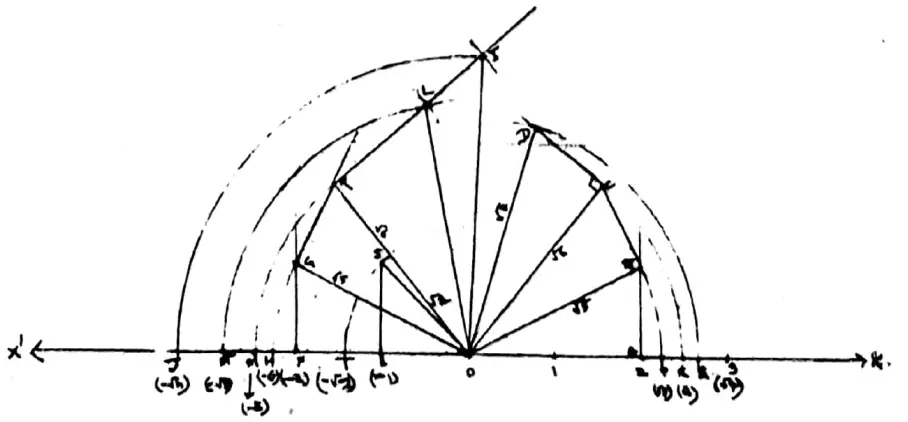
Let. 3, 2, 1, 0, 1, 2, 3 are on the number line ‘I’.
(1)Let OA = 2 unit, draw ABOA, Take AB = 1 unit.
OB & =\sqrt{O A^2+A B^2} \text { unit. } \\
& =\sqrt{4+1} \\
& =\sqrt{5} \text { unit. }
\end{aligned}\)
Taking O as the center & OB as the radius, an arc is drawn that intersects the number line at P.
∴ OP = √5 units.
By placing √5 on the number line, we get the point P.
west bengal board class 9 maths real numbers chapter solutions
(2)Now draw BC OB and take BC = 1 unit.
\(O C^2=O B^2+B C^2=(\sqrt{5})^2+1^2\) =5+1=√6 sq. unit
∴ OC = √6 units.
By placing √6 on the number line we get the point Q.
∴ OQ = √6 units.
(3)Now draw CD ⊥ OC and CD = 1 unit.
\(O D^2=O C^2+C D^2=(\sqrt{6})^2+1^2\)= 6 + 1 = 7 sq. unit
∴OD = √7 units.
By placing √7 on the number line, we get the point R.
∴OR= √7 units.
(4) Again take OE = 1 unit on the left of O, draw ES ⊥ OE, and take ES = 1 unit.
Taking O as the center & OS as the radius an arc is drawn, which intersects the number line at I.
∴ OT= – √2 unit
Now, OF = -2 unit, draw GF ⊥ OF, and take GF = 1 unit.
\(\mathrm{OG}^2=\mathrm{OF}^2+\mathrm{GF}^2=2^2+1^2\) =4+1 = 5 sq. unit
∴ OG √5 unit. Taking O as the center & OG as radius, an arc is drawn that intersects the number line at H.
∴ OH √5 units.
Now draw GK ⊥OG and take GK = 1 unit.
\mathrm{OK} & =\sqrt{O G^2+\mathrm{GK}^2} \\
& =\sqrt{(\sqrt{5})^2+1^2} \\
& =\sqrt{5+1} \\
& =\sqrt{6} \text { unit. }
\end{aligned}\)
Class 9 Maths Chapter 1 WBBSE
Taking O as a center and OK as the radius, an arc is drawn that intersects the number line at M.
∴ OM = √6 units.
(5)Again draw KL ⊥ OK, take KL = OT (= √2)
\(\begin{aligned}\mathrm{L} & =\sqrt{O K^2+\mathrm{KL}^2} \\
& =\sqrt{(\sqrt{6})^2+(\sqrt{2})^2} \\
& =\sqrt{6+2} \\
& =\sqrt{8} \text { unit. }
\end{aligned}\)
Taking O as the center and OL as the radius an arc is drawn that intersects the number line at N.
∴ON=-√8 units.
(6)From the perpendicular line on OK, cut KI = OG (√5)
∴\(\mathrm{OI}^2=\mathrm{OK}^2+\mathrm{KI}^2=(\sqrt{6})^2+(\sqrt{5})^2\) = 6 + 5 = 11
∴ OI = √11.
Taking O as centre and Ol as radius an arc is drawn which intersects the number line at J.
∴ OJ = √11 unit.
Class 9 Maths Chapter 1 WBBSE Chapter 1 Real Numbers Exercise 1.3
Question 1. Without division let’s find from the following which numbers have terminating decimals and write them.
- \(\frac{17}{80}\)
- \(\frac{13}{24}\)
- \(\frac{17}{12}\)
- \(\frac{16}{125}\)
- \(\frac{4}{35}\)
Solution:
- \(\frac{17}{80}=\frac{17}{2^4 \times 5}\)= Here denominator, 80 = 24 x 5
∴ It is a terminating decimal number (Finite).
∴ \(\frac{17}{80}\) = 0.2125 - \(\frac{13}{24}=\frac{13}{2^3 \times 3}\) = Here denominator 24 = 23 x 3
∴ It is not a terminating decimal. It will be recurring decimal number (Infinite).
∴ \(\frac{13}{24}\)= 0.541666…….. - \(\frac{17}{12}=\frac{17}{2^2 \times 3}\) = Here denominator 12 = 22 x 3
∴ It is not a terminating decimal. It will be a recurring decimal number. (Infinite)
∴ \(\frac{17}{12}\) = 1.41666……. - \(\frac{16}{125}=\frac{16}{5^3}\)= Here denominator 125 = 53
∴It is a terminating decimal number (Finite).
∴\(\frac{16}{125}\)= 0.128 - \(\frac{4}{35}=\frac{4}{5 \times 7}\) Here denominator 35 = 5 x 7
∴ It is a terminating decimal number (Infinite).
∴\(\frac{4}{35}\)=0.114285714…………
Class 9 Maths Chapter 1 WBBSE
Question 2. Let us expand each of the numbers given below into decimals and write the type of decimal expansions:
- \(\frac{1}{11}\)
- \(\frac{5}{8}\)
- \(\frac{3}{13}\)
- \(3 \frac{1}{8}\)
- \(\frac{2}{11}\)
- \(\frac{7}{25}\)
Solution:
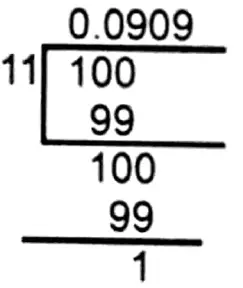
1. \(\frac{1}{11}\)
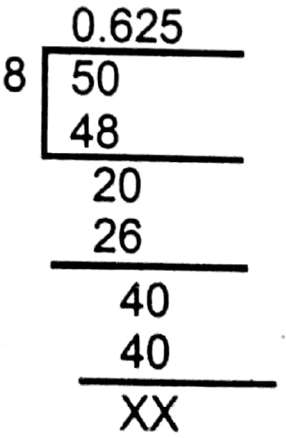
2. \(\frac{5}{8}\)
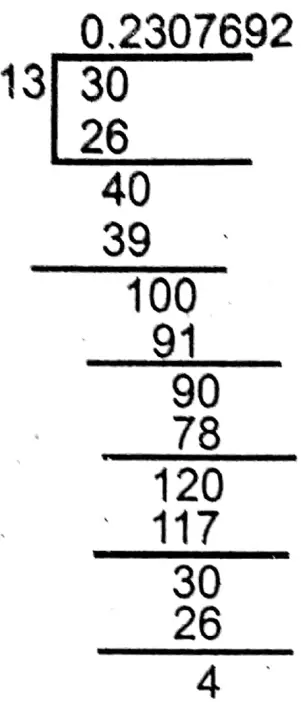
3. \(\frac{3}{13}\)
4. \(3 \frac{1}{8}\)
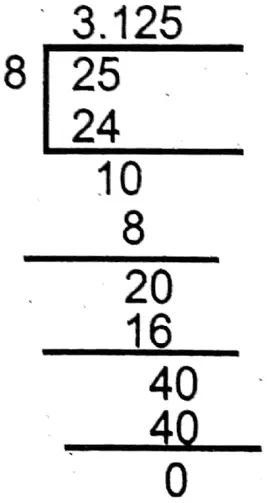
Class 9 Maths Solution West Bengal Board
5. \(\frac{2}{11}\)
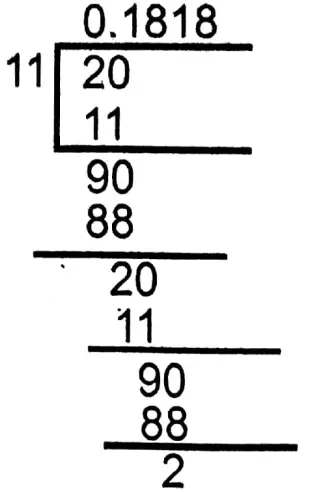
Class 9 Maths Solution West Bengal Board
6. \(\frac{7}{25}\)
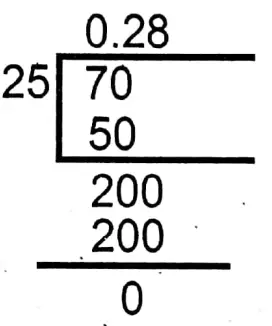
Question 3. Let us express each of the following numbers in the form of \(\frac{p}{q}\)where p & q are integers &q≠0;
- 0.3
- 1.3
- 0.54
- 0.34
- 3.14
- 0.17
- 0.47
- 0.54
- 0.001
- 0.163
Solution:
- 0.3 \(=\frac{3}{9}=\frac{1}{3}\)
- 1.3 \(1 \frac{3}{9}=1 \frac{1}{3}=\frac{4}{3}\)
- 0.54\(=\frac{54-5}{90}=\frac{49}{90}\)
- 0.34\(=\frac{34}{99}\)
- 3.14\(=\frac{314-3}{99}=\frac{311}{99}\)
- 0.17\(=\frac{17-1}{90}=\frac{16}{90}=\frac{8}{45}\)
- 0.47\(=\frac{47-4}{90}=\frac{43}{90}\)
- 0.54\(=\frac{54}{99}=\frac{6}{11}\)
- 0.001\(=\frac{001}{999}\)
- 0.163\(=\frac{163}{999}\)
wbbse class 9 maths chapter 1 real numbers notes
Question 4. Let’s write 4 numbers whose decimal expansions are non-terminating and non-recurring.
Solution:√2,√3,√5 and √7
Question 5. Let us write 3 different irrational numbers lying between \(\frac{5}{7} \& \frac{9}{7}\)
Solution:0.808008000800008, 0.858558555855558… 0.919119111911119………………
Class 9 Maths Solution West Bengal Board
Question 6. Let us write 2 different irrational numbers lying between \(\frac{3}{7} \& \frac{1}{11}\)
Solution:
- 0.121221222122221…….
- 0.373773777377779……
Question 7. Let us write the rational and irrational numbers from the following:
(1)√47
(2)√625
(3)_6.5757…
(4)1.1010010001…
Solution:
- √47 = Irrational
- √62525 = Rational
- 6.5757… = Rational
- 1.1010010001… = Irrational
Question 8. Let us place the following numbers on the number line:
1. 5.762
2. 2.321
3. 1.052
4. 4.178
Solution:
1. 5.762
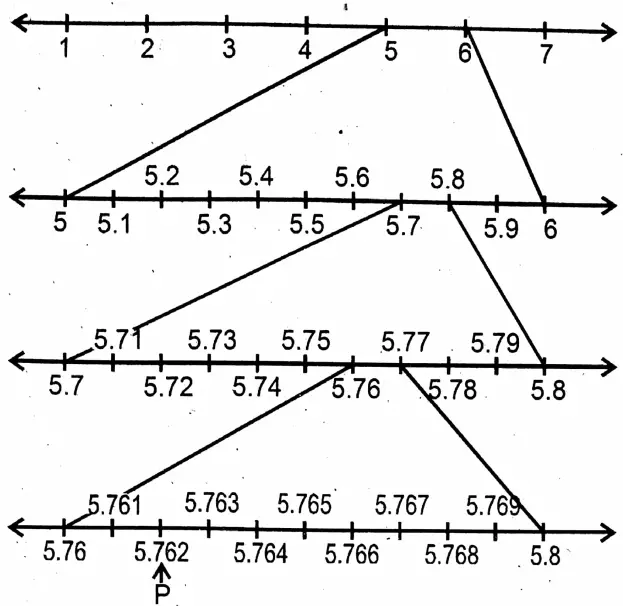
Class 9 Maths Solution West Bengal Board
∴ By placing real number 5.762 on the number line we got point P.
2. 2.321
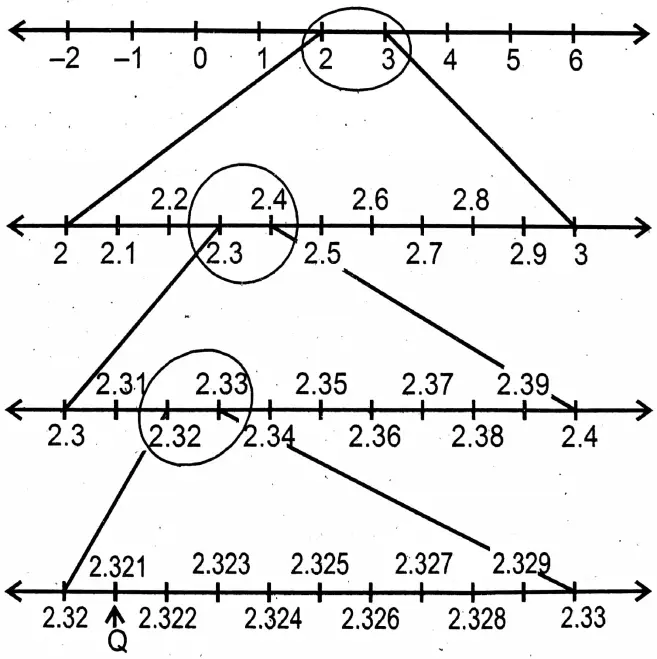
∴ By placing real number 2.321 on the number line we got point
3. 1.052
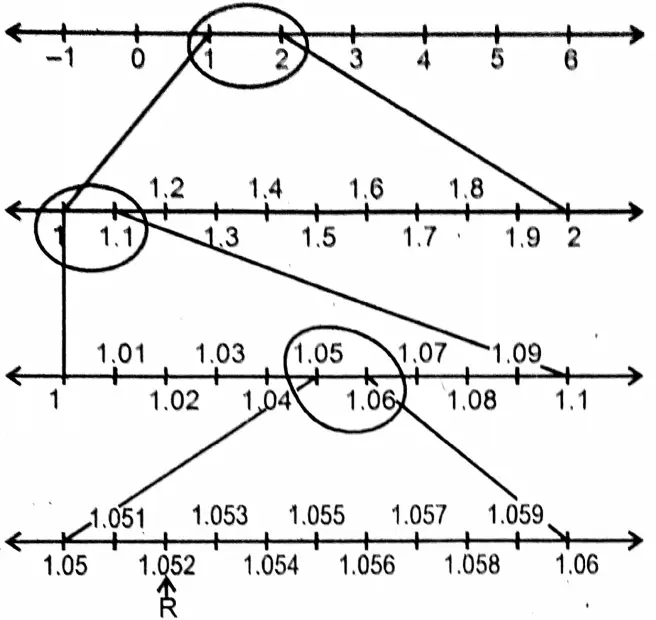
∴By placing real number 1.052 on the number line we got point R.
4. 4.178
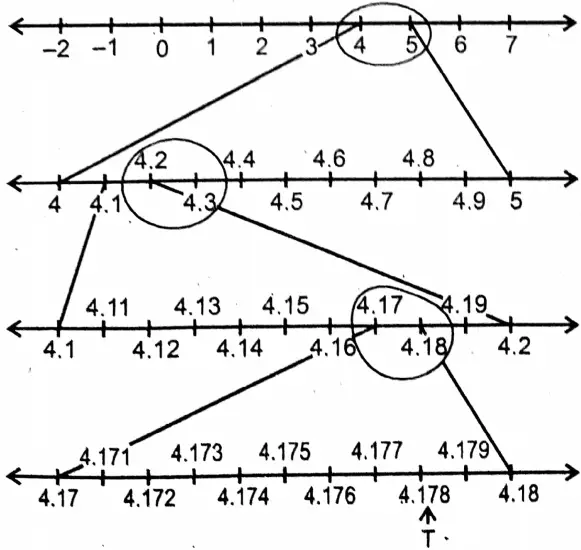
∴ By placing real number 4.178 on the number line we got point T.
Class 9 Maths Solution West Bengal Board
Question 9. Let us place the two numbers 2.23 and 5.54 upto 4 decimal places on the number line.
Solution: 2.26 = 2.2626(upto 4 decimal points)
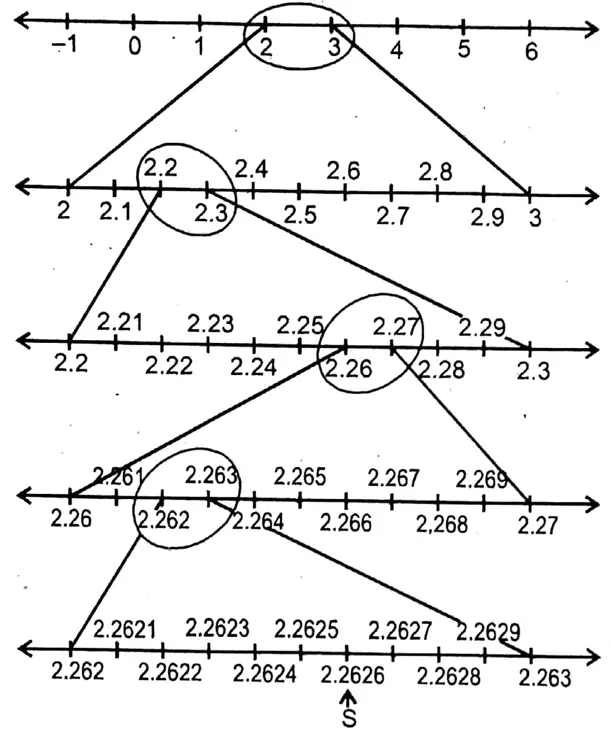
∴ By placing real number 2.2626 on the number line we got point S.
∴ 5.54 = 5.54444(Upto 4 decimal points)
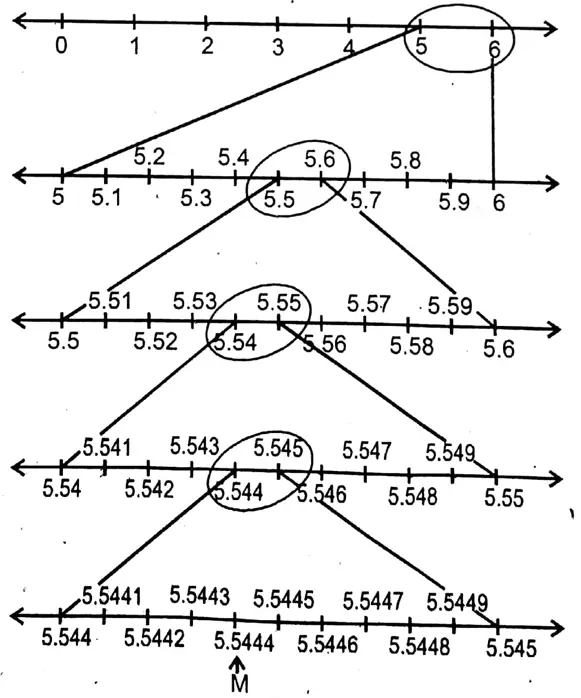
Class 9 Maths Chapter 1 WBBSE
Question 10. Let us write two rational numbers lying between 0.2323323 and 0.212112111211112…
Solution: The required two rational numbers are 0.22 and 0.023.
Question 11. Let us write two rational numbers lying between 0.2101 & 0.2222…. or 0.2.
Solution: 0.2 and 0.221
Question 12. Write ten true and ten false statements relating to real numbers, whole numbers, rational numbers and irrational numbers.
Solution: Ten true statements:
- The smallest real number is 1.
- Real numbers are infinite.
- \(\frac{2}{3}\) is a rational number. 3
- π is a irrational number.
- 100 is a whole number.
- There are infinite number of rational numbers between 2 < x < 5.
- 0 is a whole number.
- The product of two irrational numbers is always, an irrational number.
- All whole numbers are real numbers.
- The product of two rational numbers is always a rational number.
Ten false statements:
- The product of two irrational numbers is a rational number.
- 100 is the largest real number.
- 0 is not a whole number.
- \(\frac{2}{7}\) is an irrational number.
- Real numbers are infinite.
- \(\frac{1}{5}\) is a recurring rational number. 5
- 0.219 is an irrational number.
- There is only one rational number between 1 < x < 2.
- 0 is a natural number.
- 0.9 is an irrational number.
wbbse class 9 maths chapter 1 real numbers solved exercises
Question 13. Let us find how many rupees will be required to determine the values of the following expressions if Rs. 2 for one multipication and Rs. 1 for one addition is required and let us also see which law can be applied to find out the value of the expression with the least amount of money.
1. 3x2+2x+1, when x=5
2. 2x3+3x2+2x+3, when x=7 (Hints: 3×52+2×5+1=3x5x5+2×5+1, here numbers of multipications and additions are 3 & 2 respectively. So Rs. 8 is required.∴ But if we write 3x2 + 2x + 1 = x(3x+2)+ 1, by applying distributive law, then for two multipications and two additions Rs. 6 is required.).
Solution:
1. 3x2 + 2x + 1 = 3 x 52+2 x 5+1 =3x5x5+2×5+1 total cost for 3 multiplications and 2 additions = 3 Χ 2+2 x 1 = Rs. 8
Again: 3×2 + 2x + 1 = x(3x+2)+ 1 total cost for 2 multiplications and 2 additions = 2 x 2 + 2 × 1 = Rs. 6
The second law can be applied with least amount of money.
2. 2x3 + 3x2 + 2x + 3 =2x( x2+ 1) + 3(x2 + 1) = (2x+3) (x2 + 1)
∴ Total cost for 4 mulltiplications and 2 additions will be = 4×2+2×1 = Rs. 10.
Class 9 Mathematics West Bengal Board
Question 14.
1. The decimal expansion of √5 is
(1) A terminating decimal
(2) A terminating or recurring decimal
(3) Non-terminating and non-recurring decimal
(4) None of them
Solution: (3) a non-terminating and non-recurring decimal
2. The product of two irrational numbers is
(1) Always irrational number
(2) Always Rational Number
(3) Always an integer
(4) Rational or irrational number
Solution: (4) rational or irrational number
3. π and 22/7 are
(1) Always rational number
(2) Always Irrational number
(3) π is rational and is irrational
(4) π is irrational and 22/7 is rational
Solution: (4) π is irrational and 22/7 is rational
4. Between two rational numbers, there exists
(1)No rational number
(2)Only one rational number
(3)Infinite numbers of rational numbers
(4)No irrational number
Solution: (3)Infinite numbers of rational numbers
5. Between two irrational numbers, there exists
(1)No rational number
(2)Only one rational number
(3)Infinite numbers of irrational numbers
(4)No irrational number
Solution: (3) infinite numbers of irrational numbers
6. The number 0 is
(1)Whole number but not integer
(2)Integer but not rational
(3)Rational but not real number
(4)Whole number, integer, rational and real number but not irrational
Solution: (4)Whole number, integer, rational and real number but not irrational
Class 9 Mathematics West Bengal Board
Question 15. Short-answer type questions :
- Let us write a number where the sum of two irrationals is rational.
Solution: Two irrational numbers are √5 and -√5.
Sum of √5 and√5 = √5+(-√5) = √5-√5 = 0 = Rational number
∴ Number = 0 - Let us write a number where the difference of two irrationals is a rational number.
Solution: Two irrational numbers are = (√7+2) and (√7-2)
Difference of (√7+2) and (7-2)- (√7+2)-(√7-2) = 4 = Rational number
∴ Number = 4 - Let us write a rational number lying between 1/7 and 2/7.
Solution: \(=\frac{1}{2}\left(\frac{1}{7}+\frac{2}{7}\right)=\frac{3}{14}\) - Let us write an irrational number lying between \(\frac{1}{7} \text { and } \frac{2}{7}\)
Solution:\(\frac{1}{7}\)= 0.142857
\(\frac{2}{7}\)= 0285714
∴ \(\frac{1}{7} \text { and } \frac{2}{7}\) = 0.1515515551 - Let us write the common fraction of the recurring decimal 0.0123
Solution: 0.0123 \(=\frac{123-12}{10000-1000}=\frac{111}{9000}=\frac{37}{3000}\)
