Chapter 12 Theorems On Area Exercise 12
Question 1. P and Q are the midpoints of sides AB and DC of parallelogram ABCD, let’s prove that the area of quadrilateral field = \(\frac{1}{2}\) x area of parallelogram field.
Solution:
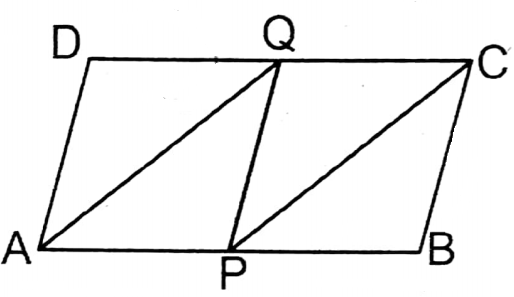
Join: P, Q.
Proof: ∵ P is the midpoint of AB
∴ AP = \(\frac{1}{2}\) AB
= \(\frac{1}{2}\) DC [∵ opposite sides of parallelogram]
= QC (∵ Q is the midpoint of CD)
Read and Learn More WBBSE Solutions For Class 9 Maths
In □PCQ, AP = QC & AP II QC (∵ AB II DC)
∴ APCQ is a parallelogram.
In □PQD, AP II DQ & AP = DC
∴ APQD is a parallelogram.
In □PBCQ, PB = QC & PB II QC
∴ PBCQ is a parallelogram.
∴ Area of quadrilateral APCQ = ΔAPQ+ΔPCQ
= \(\frac{1}{2}\) parallelogram □APQD + \(\frac{1}{2}\) parallelogram □PBCQ
= \(\frac{1}{2}\) (parallelogram □APQD+ parallelogram □PBCQ)
= \(\frac{1}{2}\) Area of parallelogram ABCD Proved
Question 2. The distance between two sides AB and DC of a rhombus ABCD is PQ and the distance between sides AD and BC is RS; let’s prove that PQ = RS.
Solution:
To prove PQ = RS.
Proof: ∵ Area of rhombus = base x height
∴ Area of rhombus ABCD = AB.PQ
Again, the area of rhombus ABCD = BC.RS
∴ AB.PQ=BC.RS
∴ As AB = BC (Side of the rhombus)
∴ PQ = RS Proved
Question 3. P and Q are the mid-points of sides AB and DC of parallelogram ABCD respectively. Let’s prove that PBQD is a parallelogram and ΔPBC= \(\frac{1}{2}\) parallelogram PBQD.
Solution:
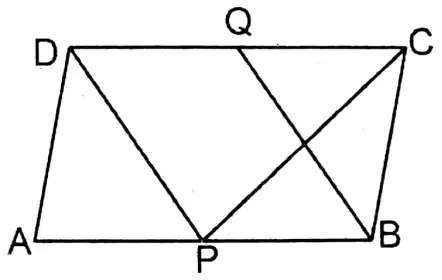
To prove
1. PBQD is a parallelogram
2. ΔPBC = \(\frac{1}{2}\) Parallelogam PBQD
Join: P & C.
Proof: ∵ ABCD is a parallelogram.
∴ AB = DC
or, \(\frac{1}{2}\) AB= \(\frac{1}{2}\) DC
or, PB = DQ (∵ P & Q are the mid-points of the sides AB & DC respectively)
In parallelogram □PBQD, PB = DQ & PB II DQ (∵ AB II DC)
∴ PBQD is a parallelogram …… (1)
∴ ΔPBC & parallelogram PBQD are on the same base PB & between the same parallel straight lines PB & DC.
∴ ΔPBC = \(\frac{1}{2}\) parallelogram □PBQD ….(2) Proved
Question 4. In an isosceles triangle, ABC, AB = AC, and P is any point on produced side BC. PQ and PR are perpendicular on sides AB and AC from the point P respectively. BS is perpendicular on side AC from point B; let’s prove that PQ-PR = BS.
Solution:
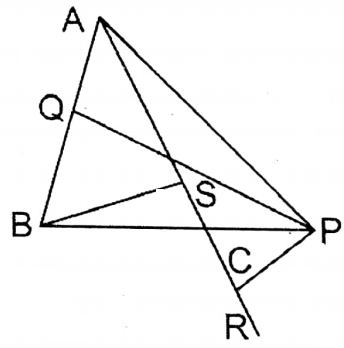
To prove, PQ-PR = BS
Join: P, Q.
Proof: Area ΔABP = area of ΔABC+ area of ΔAPC
or, \(\frac{1}{2}\) . AB.CQ = \(\frac{1}{2}\) AC.BS+ \(\frac{1}{2}\) .AC.PR
,or, AB.PQ = AC(BS +PR)
or, AC. PQ AC (BS+ PR) (∵ AB = AC)
or, PQ=BS + PR
or, PQ-PR = BS Proved
Question 5. O is any point outside the equilateral triangle ABC and within the angular region on ABC; OP, OQ and OR are the perpendicular distances of AB, BC, and CA respectively from the point O. Let us prove that the altitude of the triangle = OP + OQ – OR.
Solution:
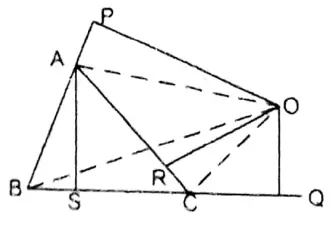
To prove the Height of the triangle = OP + OQ – OR.
Join: O, A; O, B and O, C & AS is the perpendicular from A on BC.
Proof : ΔABC = ΔAOB + ΔBOC – ΔAOC
or, \(\frac{1}{2}\).BC.AS = \(\frac{1}{2}\).AB.OP+\(\frac{1}{2}\).BC.OQ – \(\frac{1}{2}\) AC.OR
or, BC.AS = BC. OP+ BC. OQ – BC. OR [∵ AB = BC = AC]
or, AS OP + OQ – OR
or, Height of the triangle = OP+OQ-OR Proved
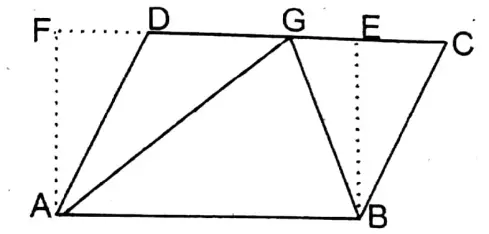
Question 6. A straight line parallel to AB of parallelogram ABCD intersects sides AB, AC, and BC or their produced parts at the points E, F, and G respectively. Let’s prove that ΔAEG = ΔAFD.
Solution:
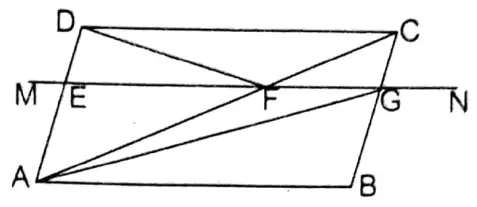
To prove ΔAEG = ΔAFD
Join: A, G & D, F.
Proof: ΔACG & parallelogram CDEG are on the same base CG & in between two parallelogram lines CG & AD.
∴ ΔACG = \(\frac{1}{2}\) parallelogram □CDEG
Again, ΔCDF & parallelogram □CDEG are on the same base & in between two parallel lines CD & EG.
∴ ΔCDF = \(\frac{1}{2}\) parallelogram □CDEG
∴ ΔACG = ΔCDF …..(1)
∵ AC is the diagonal of parallelogram ABCD.
∴ ΔABC = ΔADC ……(2)
Subtracting (1) from (2), ΔABC – ΔACG = ΔADC – ΔCDF
or, ΔABG = ΔAFD
or, ΔAEG = ΔAFD ( ∵ AG is the diagonal of the parallelogam ABGE)
∴ ΔABG = ΔAEG Proved
Question 7. E is any point on side DC of parallelogram ABCD, produced AE meets produced BC at the point F. D, F are joined. Let’s prove that (1) ΔADF= ΔABE; (2)ΔDEF = ΔBEC.
Solution:
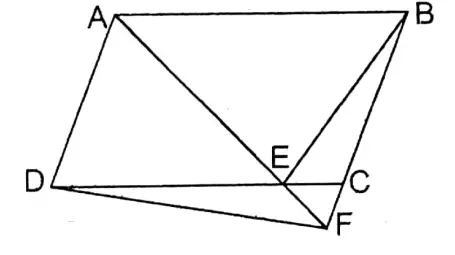
Join: D, F. To prove (1) ΔADF = ΔABE (2) ΔDEF = ΔBEC.
Proof: ΔADF & parallelogram ABCD are on the same base AD & in between two parallelograms AD & BF
∴ ΔADF = \(\frac{1}{2}\) parallelogram □ABCD
Again, ΔABE & parallelogram □ABCD are on the same base AB & between two parallel straight lines AB & DC.
∴ ΔABE = \(\frac{1}{2}\) parallelogram □ABCD
∴ ΔADF = ΔABE
∴ ΔADE+ ΔBEC = \(\frac{1}{2}\) □ABCD
or, ΔADE+ ΔBEC = ΔADF
or, ΔADE + ΔBEC = ΔADE + ΔDEF
or, ΔBEC = ΔDEF
or, ΔDEF = ΔBEC
Question 8. Two triangles ABC and ABD with equal area stand on the opposite side of AB. Let’s prove that AB bisects CD.
Solution:
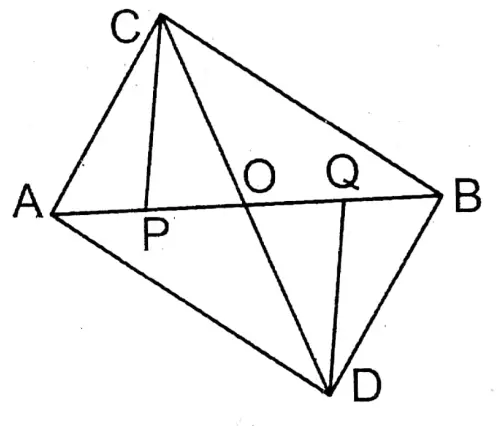
To prove AB bisects CD.
CP & DQ are two perpendiculars drawn on AB from points C & D respectively. CD cuts AB at O.
Proof: ∵ΔABC= ΔABD (given)
∴ \(\frac{1}{2}\).AB.OP = \(\frac{1}{2}\).AB.DQ
or, CP = DQ
In ΔCOP & ΔDOQ,
CP = DQ (proved)
∠CPO = ∠DQO (= 90°)
∠COP = vertically opposite ∠DOQ
∴ ΔCPO = ΔDOQ (A-A-S condition)
∴ CO = OD
∴ AB bisects CD. Proved
Question 9. D is midpoint of side BC of triangle ABC. Parallelogram CDEF stands between side BC and parallels to BC through point A. Let’s prove that ΔABC = parallelogram □CDEF.
Solve: To prove AABC = parallelogram CDEF.
Solution:
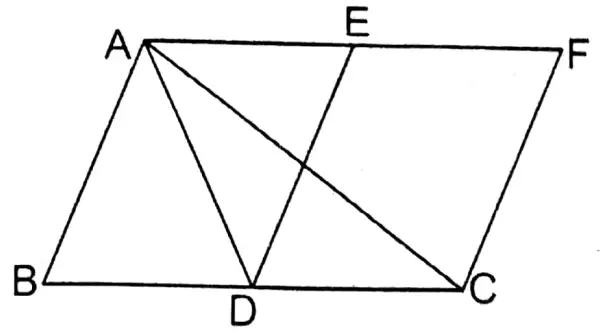
Join: A, D.
Proof: ΔADC & parallelogram CDEF are on the same base CD & in between two parallel straight lines CD & AF.
∴ ΔADC = \(\frac{1}{2}\) parallelogram □CDEF
∵ AD is the median of ΔABC
∴ ΔADC = \(\frac{1}{2}\) ΔABC
∴ \(\frac{1}{2}\) ABC = parallelogram □CDEF
or, ΔABC = parallelogram □CDEF Proved
Question 10. P is any a point on diagonal BD of parallelogram ABCD. Let’s prove that ΔAPD = ΔCPD.
Solution:
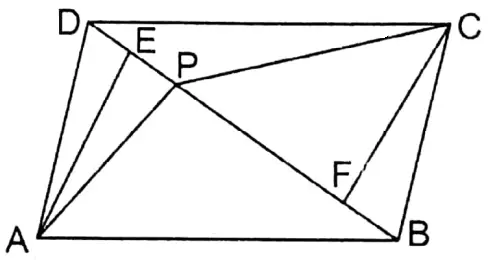
To prove ΔAPD = ΔCPD
AE & CF are two perpendiculars on BD from points A & C respectively.
Proof: In ΔADE ΔBCF
∠ADE = alternate ∠CBF
∠AED = ∠CFB
& AD = BC
∴ ΔADE ≅ ΔBCF
∴ AE = CF
(∵ AD II BC & BD is the transversal)
[each angle is 90°]
(∵ opposite side of parallelogram)
(A-A-S condition)
As ΔAPD & ΔCPD are on the same base DP
∴ Their heights are equal.
∴ AE = CF
∴ ΔAPD = ΔCPD Proved
Question 11. AD and BE are the medians of triangle ABC. Let’s prove that ΔACD = ΔBCE
Solution:
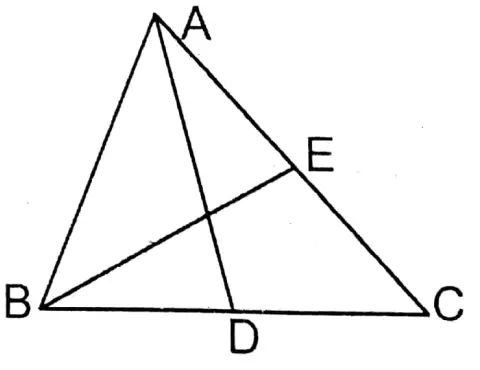
In ΔABC, AD & BE are the medians.
To prove: ΔACD = ΔBCE
Proof: In ΔABC is the median.
∴ ΔACD = ΔABD = \(\frac{1}{2}\) ΔABC
Again, In ΔABC, BE is the median.
∴ ΔBCE = \(\frac{1}{2}\) ΔABC
∴ ΔACD = ΔBCE Proved
Question 12. A line parallel to BC of triangle ABC intersects sides AB and AC at the points P and Q respectively. CQ and BQ intersect each other at the point X. Let’s prove that:
1. ΔBPQ= ΔCPQ
2. ΔBCP = ΔBCQ
3. ΔACP= ΔABQ
4. ΔBXP = ΔCXQ
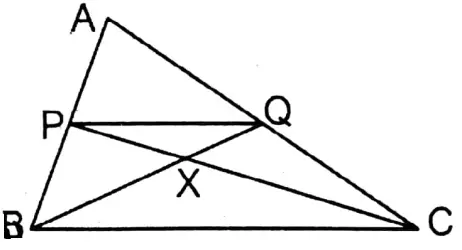
Solution: To prove
1. ΔBPQ= ΔCPQ
2. ΔBCP = ΔBCQ
3. ΔACP= ΔABQ
4. ΔBXP = ΔCXQ
Proof: ΔBPQ & ΔCPQ are on the same base PQ & in between two parallel lines PQ & BC.
∴ ΔBPQ = ΔCPQ ….(1)
ΔBCP & ΔBCQ are on the same base BC & in between two parallel lines PQ & BC.
∴ ΔBCP = ΔBCQ …(2)
∵ ΔBPQ = ΔCPQ (Proved)
∴ ΔBPQ+ΔAPQ = ΔCPQ + ΔAPQ
∴ ΔABQ = ΔACP
∴ ΔACP = ΔABQ
∵ ΔBPQ = ΔCPQ
∴ ΔBPQ – ΔPQX = ΔCPQ = ΔPQX
∴ ΔBXP = ΔCXQ …..(4) Proved
Question 13. D is the mid-point of BC of triangle ABC and P is any point on BC. Join P,A. Through the point D a straight line parallel to line segment PA meets AB at point Q. Let’s prove that:
1. ΔADQ= ΔPDQ
2. ΔBPQ= \(\frac{1}{2}\) ΔABC.
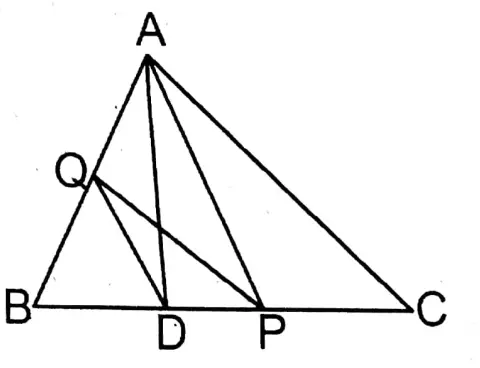
Solution: D is the mid-point of BC of triangle ABC and P is any point on BC. P and A are joined. Through the point D a straight line parallel to line segment PA meets AB at point Q.
To prove :
1. ΔADQ= ΔPDQ
2. ΔBPQ= \(\frac{1}{2}\) ΔABC.
Proof: ΔADQ and ΔPDQ lie on the same base DQ and between the same parallel straight lines DQ and AP.
∴ ΔADQ ΔPDQ
∴ ΔADQ = ΔPDQ ….(1)
∴ ΔADQ+ΔBDQ = ΔPDQ + ΔBDQ
∴ ΔABD = ΔBPQ
∵ AD is the median of ΔABC.
∴ ΔΑΒD = \(\frac{1}{2}\) ΔΑΒC
∴ ΔBPQ = \(\frac{1}{2}\) ΔABC ….(2)
Question 14. In triangle ABC of which AB = AC; perpendiculars through the points B and Con sides AC and AB intersect sides AC and AB at the points E and F. Let’s prove that FE II BC.
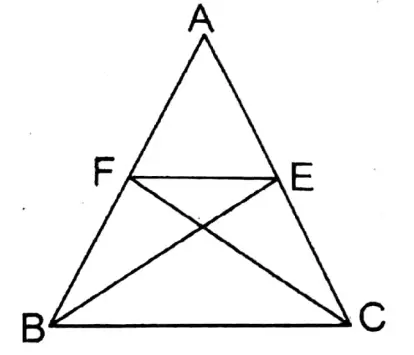
Solution: To prove FE II BC
Join E, F.
Proof: In ΔABC, AB = AC
∴ ∠ABC = ∠ACB
∴ ∠FBC= ∠ECB
In ΔBCF & ΔBCE
∠FBC=∠ECB Proved
∠BFC = ∠BEC (= 90°)& BC is the common base
∴ ΔBCF ≅ ΔBCE (A-A-S condition)
∴ Area of ΔBCF = Area of ΔBCE
∴ ΔBCF & ΔBCE are on the same base BC & their areas are equal.
∴ The triangles are in between two parallel lines.
∴ FE II BC Proved
Question 15. In triangle ABC, ∠ABC= ∠ACB; bisectors of an angle ∠ABC and ∠ACB intersect the sides AC and AB at the points E and F respectively. Let’s prove that FE II BC.
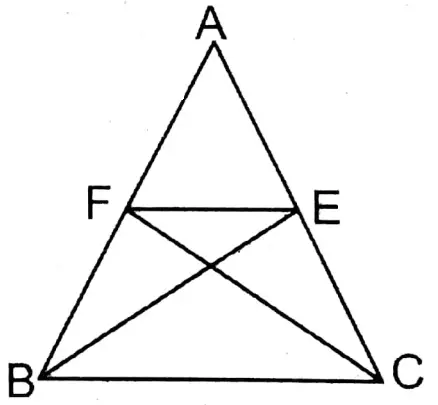
Solution: To prove FE II BC
Join: E, F
Proof: In ΔABC, ΔABC ΔACB
∴ \(\frac{1}{2}\) ∠ABC = \(\frac{1}{2}\) ∠ACB
∴ ∠EBC = ∠FCB
In ΔBCF & ΔBCE
∠FBC =∠ECB (∵∠ABC = ∠ACB)
∠FCB = ∠EBC (Proved) & BC is the common side.
∴ ΔBCF ≅ ΔBCE (A-A-S Condition)
∴ Area of ΔBCF = Area ΔBCE
∴ ΔBCF & ΔBCE on the same BC & their areas are equal.
∴ The triangles are in between two parallel lines.
∴ FE II BC
Question 16. The shape of two parallelograms ABCD and AEFG, of which ∠A is common, are equal in area and E lies on AB. Let’s prove that DE II FC.
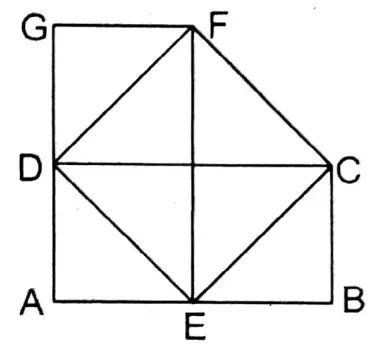
Solution: To prove DE II FC.
Join: D, E; E, C & C, F.
Proof: ΔDEC and parallelogram ABCD are on the same base & in between two parallel lines AB & CD.
∴ ΔDEC = \(\frac{1}{2}\) parallelogram □ABCD
Again, ΔDEF & parallelogram AEFG are on the same base & in between two parallel lines EF & AG.
∴ ΔDEF = \(\frac{1}{2}\) parallelogram □AEFG
∵ parallelogram □ABCD = parallelogram □AEFG (given)
∴ \(\frac{1}{2}\) parallelogram □ABCD = \(\frac{1}{2}\) parallelogram □AEFG
∴ ΔDEC = ΔDEF
ΔDEC & ΔDEF are on the same base DE & their areas are equal.
∴ DE II FC Proved
Question 17. ABCD is a parallelogram and ABCE is a quadrilateral. Diagonal AC divides the quadrilateral field ABCE into two equal parts. Let’s prove that AC II DE.
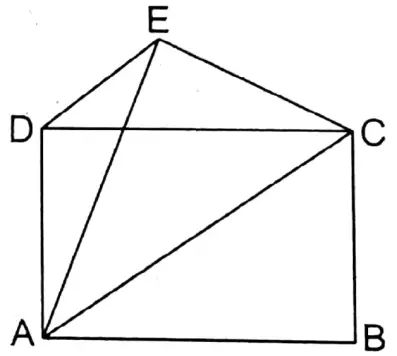
Solution: To prove AC II DE.
Join D, E.
Proof: Diagonal AC bisects quadrilateral ABCD in two equal parts.
∴ Area of AABC = Area of AACE
Again, in the triangle ABC,
∴ Area of ΔABC = Area of ΔADC
∴ Area of ΔADC = Area of ΔACE
∴ ΔADC & ΔACE are of equal area & on the same base.
∴ Triangles are in between two parallel lines.
∴ AC II DC Proved
Question 18. D is the mid-point of side BC of triangle ABC; P and Q lie on sides BC and BA in such a way that ΔBPQ = \(\frac{1}{2}\) ΔABC. Let’s prove that, DQ II PA.
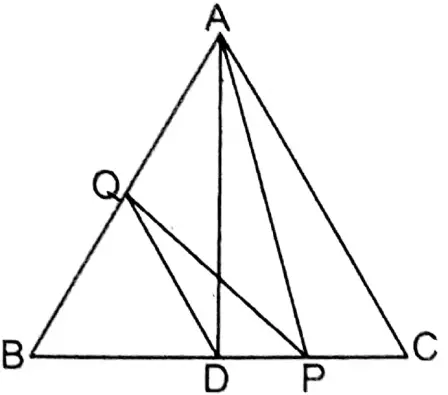
Solution: To prove DQ II PA.
Join A, D.
Proof: In ΔABC, D is the mid-point of BC.
∴ AD is the median.
∴ ΔABD = \(\frac{1}{2}\) ΔABC
But ΔBPQ = \(\frac{1}{2}\) ΔABC (given)
∴ ΔABD = ΔBPQ
∴ ΔABD-ΔBDQ= ΔBPQ-ΔBDQ
∴ ΔADQ = ΔDPQ
∴ ΔADQ & ΔDPQ are of equal area and on the same base DQ.
∴ DQ II PA Proved
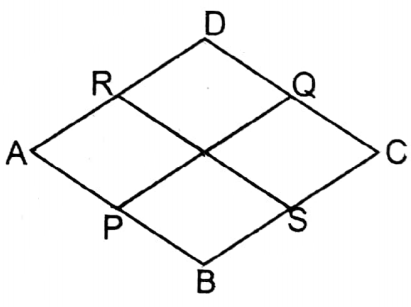
Question 19. Parallelogram ABCD, of which mid-points of sides AB, BC, CD are E, F, G and H, and DA respectively. Let’s prove that:
1. EFGH is a parallelogram.
2. Area of the shape of parallelogram EFGH is half of the area of the shape of parallelogram ABCD.
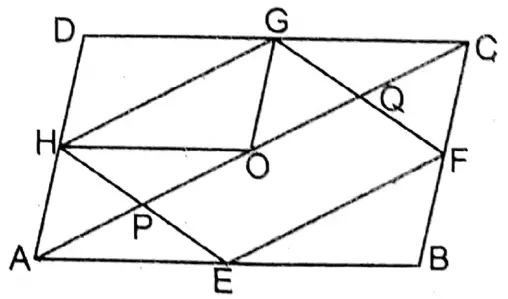
Solution: To prove EFGH is a parallelogram.
Join: A, C
Proof:
1. In ΔABC, E & F are the mid-points of AB & AC.
∴ EF II AC & EF = \(\frac{1}{2}\) AC …….(1)
Again, in ΔADC, the mid-points of AD & CD are H & G.
∴ HG II AC & HG=\(\frac{1}{2}\) AC …….(2)
From (1) & (2), EF II HG & EF = HG
∴ EFGH is a parallelogram.
2. O is the midpoint of AC. Join H, O & G, O. HE & GF cut AC at P & Q. In ΔDAC joining the mid-points of the sides AD, AC & CD, AHOG is formed.
∴ ΔHOG = \(\frac{1}{4}\) ΔABC
∵ HG II PQ
∴ ΔHOG = \(\frac{1}{2}\) parallelogram □HPQG
[ ∵ ΔHOG & parallelogram □HPQG are on the same base HG and in between two parallel lines HG & PQ]
∴ parallelogram □HPQG = 2ΔHOG = 2 x \(\frac{1}{4}\) ΔACD = \(\frac{1}{2}\) ΔACD
Similarly, parallelogram □EPQF = \(\frac{1}{2}\) ΔABC
∴ parallelogram □HPQG + parallelogram □EPQF = \(\frac{1}{2}\) ΔACD + \(\frac{1}{2}\) ΔABC
∴ parallelogram □EFGH = \(\frac{1}{2}\) ( ΔACD+ ΔABC) = \(\frac{1}{2}\) parallelogram □ABCD ….(2) Proved
Question 20. In of a trapezium ABCD, AB II DC and E is mid-point of BC. Let’s prove that area of triangular field AED = \(\frac{1}{2}\) Χ area of the shape of the trapezium field ABCD.
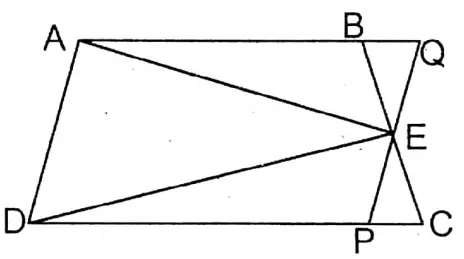
Solution: In trapezium ABCD, AB II CD and E is the mid-point of BC.
Let’s prove that in the triangular field = area \(\frac{1}{2}\) x ABCD of the trapezium field.
Construction: From point E parallel to AD a straight line is drawn which cuts DC at P and extended AB at Q. A, and E are joined.
Proof: ΔAED & parallelogram □ADPQ are on the same base AD & in between two parallel lines AD and PQ.
∴ Area of ΔAED = \(\frac{1}{2}\) parallelogram □ADPQ
In ΔPEC & ΔBEQ,
∠PCE = alternate ∠EBQ
∠PEC (vertically opposite angle) ∠BEQ & CE = BE (∵ E is the midpoint of BC)
∴ ΔPEC ≅ ΔBEQ (A-A-S Condition)
∴ Area of ΔPEC = Area ΔBEQ
Area of ABCD trapezium = Area ADPEB + Area ΔPEC
= Area of ADPEB + Area of ABEQ
= Area □ADPQ
= Area 2x ΔAED
∴ 2 x area ΔAED = Area of ABCD trapezium
∴ Area ΔAED = \(\frac{1}{2}\) Χ Area of ABCD trapezium
Question 21. Multiple choice questions
1. D, E, and F are mid-points of sides BC, CA, and AB respectively of a triangle ABC. If AABC= 16 sq. cm, then the area of the shape of trapezium FBCE is
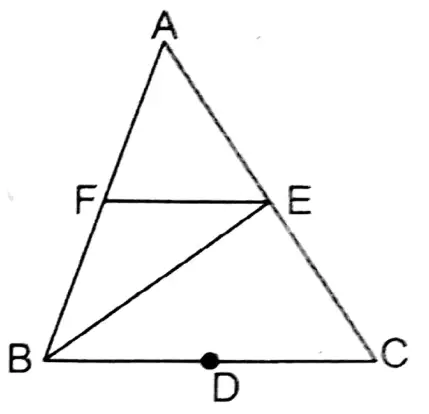
1. 40 sq. cm
2. 8 sq. cm
3. 12 sq. cm
4. 100 sq. cm
Solution: Join B, E.
∵ BE is the median of ΔABC.
∴ Area ΔABE = Area ΔBEC = Area \(\frac{1}{2}\) ΔABC
= \(\frac{1}{2}\) x 16 sq cm= 8 sq cm
∵ EF is the median of ΔABE
∴ Area ΔBEF= Area \(\frac{1}{2}\) ΔABE
= \(\frac{1}{2}\) x 8 sq cm = 4 sq cm
Area FBCE = Area ΔBEF + Area ΔBCE = (4+8) sq. cm = 12 sq. cm
Solution: 3.12 sq. cm
2. A, B, C, and D are the mid points of sides PQ, QR, RS, and SP respectively of parallelogram PQRS. If the area of the shape of the parallelogram PQRS = 36 sq. cm then the area of the ABCD field is
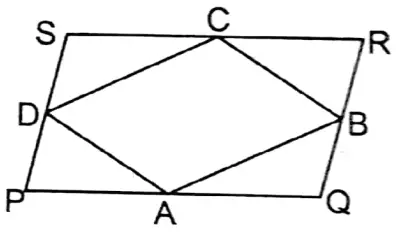
1. 24 sq. cm
2. 18 sq. cm
3. 30 sq. cm
4. 36 sq. cm
Solution: We know the area of the parallelogram formed by joining the midpoints of a parallelogram is half of that parallelogram.
∴ Area of ABCD = \(\frac{1}{2}\) Χ Area of parallelogram □PQRS
= \(\frac{1}{2}\) x 36 sq. cm = 18 sq. cm
Solution: 2. 18 sq. cm
3. O is any point inside parallelogram ABCD. If AAOB +ACOD = 16 sq. cm, then area of the shape of parallelogram ABCD is
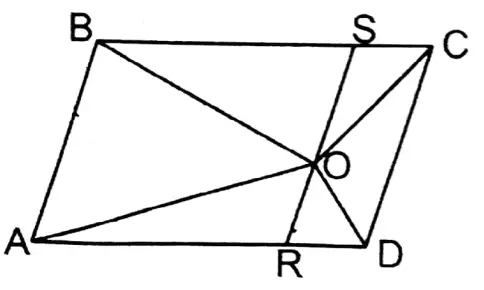
1. 8 sq. cm
2. 4 sq. cm
3. 32 sq. cm
4. 64 sq. cm
Solution: The straight line through O & parallel to AB intersects AD & BC at R & S points respectively.
∴ ΔΑΟΒ = \(\frac{1}{2}\) parallelogram □ARSB
∴ ΔCOD = \(\frac{1}{2}\) parallelogram □CSRD
∴ ΔAOB + ΔCOD = \(\frac{1}{2}\) (parallelogram □ARSB+ parallelogram □CSRD)
∴ ΔAOB+ ΔCOD = \(\frac{1}{2}\) Χ parallelogram □ABCD
or, 16 sq. cm = \(\frac{1}{2}\) parallelogram □ABCD
∴ Area of parallelogram ABCD = 2 x 16 sqcm = 32 sqcm
Solution: 3. 32 sq. cm
4. D is the mid-point of side BC of triangle ABC. E is the mid-point of side BD and O is the mid-point of AE; the area of triangular field BOE is
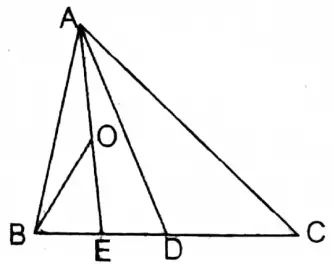
1. \(\frac{1}{3}\) Χ Area of ΔABC
2. \(\frac{1}{4}\) Χ Area of ΔABC
3. \(\frac{1}{6}\) Χ Area of ΔABC
4. \(\frac{1}{8}\) Χ Area of ΔABC
Solution:
Area of the triangular area BOE = \(\frac{1}{2}\) x area ΔABE [ ∵BO is the median of ΔABE]
\(\frac{1}{2}\) x \(\frac{1}{2}\) x area ABC (∵ In ΔABE, BO is the median)
\(\frac{1}{2}\) x \(\frac{1}{2}\) x area ABD (∵ In ΔABD, AE is the median)
=\(\frac{1}{2}\) X \(\frac{1}{2}\) X \(\frac{1}{2}\) x area ABC (∵ In ΔABC, AD is the median)
= \(\frac{1}{8}\) X ABC
Solution: 4. \(\frac{1}{8}\) X Area of ΔABC
5. A parallelogram, a rectangle, and a triangle stand on the same base and between the same parallel, and if their areas are P, Q, and T respectively then
1. P=R=2T
2. P=R= \(\frac{T}{2}{/latex]
3. 2P = 2R = T
4. P=R=T
Solve: Let parallelogram ABCD, rectangle ABEF and AABG are situated on same base AB and in between parallel straight lines AB and FC.
Area of parallelogram □ABCD = Area of rectangle ABEF =2 x area ΔAGB
∴ P = R = 2T
Solution: 1. P=R=2T
Question 22. Short answer type questions :
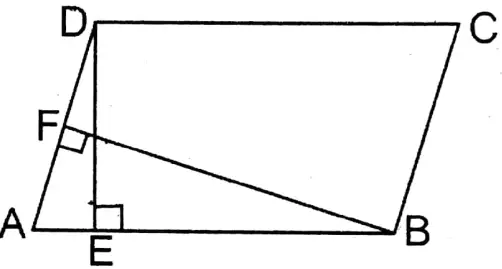
1. DE is perpendicular on side AB from point D of parallelogram ABCD and BF is perpendicular on side AD from the point B; if AB = 10 cm, AD = 8 cm, and DE = 6 cm, let us write how much is length of BF.
Solution:
Given
DE is perpendicular on side AB from point D of parallelogram ABCD and BF is perpendicular on side AD from the point B; if AB = 10 cm, AD = 8 cm, and DE = 6 cm
Area of parallelogram ABCD = Base x height = 10 x 6 sq. cm
= 60 sq. cm
∴ BF is the height of parallelogram □ABCD
∴ ADX BF = Area of parallelogram □ABCD
or, 8 x BF 60 cm
or, BF = [latex]\frac{60}{8}\) sq. cm
or, BF = 7.5 cm
∴ Length of BF = 7.5 cm
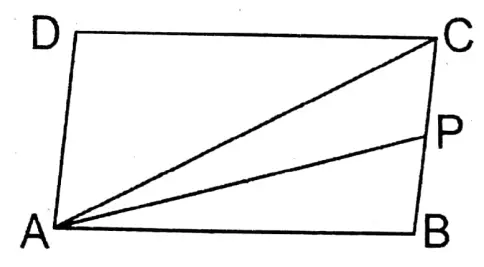
2. The area of the shape of parallelogram ABCD is 100 sq units. P is the mid-point of side BC; let us write how much is the area of the triangular field ABP.
Solution:
Given
The area of the shape of parallelogram ABCD is 100 sq units. P is the mid-point of side BC
Join, A, P, and A, C.
Area of ΔABP = Area of \(\frac{1}{2}\)× ΔABC (: AP is the median of ΔABC)
\(\frac{1}{2}\) x \(\frac{1}{2}\) Χ ABCD Area of parallelogram
= \(\frac{1}{4}\) x 100 sq.cm = 25 sq.cm
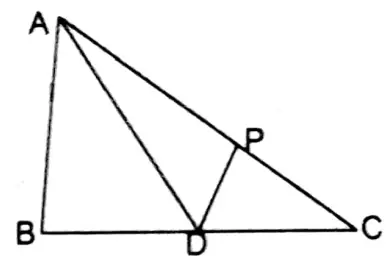
3. AD is the median of triangle ABC and P is any point on side AC in such a way that area of ΔADP area of ΔABD = 2: 3. Let us write the ratio, area of ΔPDC area of ΔABC.
Solution:
Given
AD is the median of triangle ABC and P is any point on side AC in such a way that area of ΔADP area of ΔABD = 2: 3.
Let the area of ΔADP & ΔABD be 2x sq. unit & 3x sq. unit respectively.
∵ AD is the median.
∴ Area of ΔACD = Area of ΔABD = 3x sq. cm
∴ Area of ΔPDC = Area of ΔACD = Area of ΔADP
=(3x-2x) sq.cm = x sq. cm
Area of ΔABC = Area of ΔABD + Area of ΔACD =(3x + 3x) sq.cm = 6x sq. cm
∴ Area of ΔPDC: Area of ΔABC =x:6x = 1:6
4. ABDE is a parallelogram. F is the midpoint of side ED. If the area of the triangular field ABD is 20 sq. unit, then let us write how much is an area of the triangular field AEF.
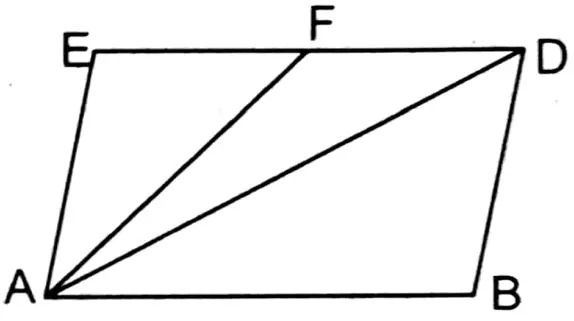
Solution:
Given
ABDE is a parallelogram. F is the midpoint of side ED. If the area of the triangular field ABD is 20 sq. unit,
∵ AD is the diagonal of the parallelogram ABDE.
∴ Area of ΔAED = Area of ΔABD = 20 cm
∴ In ΔAED, is the median AF,
∴ Area of ΔAEF = Area of \(\frac{1}{2}\) ΔAED
= \(\frac{1}{2}\) x 20 sq.cm = 10 sq.cm.
5. PQRS is parallelogram. X and Y are the mid-points of sides PQ and SR respectively. Construct diagonal SQ. Let us write the area of the shape of parallelogram field XQRY: area of triangular field QSR.
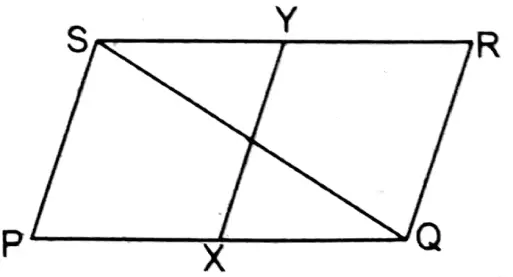
Solution:
Given
PQRS is parallelogram. X and Y are the mid-points of sides PQ and SR respectively.
X & Y are the mid-points of PQ & SR respectively.
∴ Area of parallelogram □XQRY = \(\frac{1}{2}\) of Area of parallelogram PQRS
∵ SQ is the diagonal of the parallelogram PQRS.
∴ Area of ΔQSR = \(\frac{1}{2}\) x Area of the parallelogram PQRS
∴ Area of parallelogram □XQRY = Area of ΔQSR
∴ Area of the parallelogram XQRY: Area of ΔQRS = 1:1
