Chapter 13 Construction Exercise 13
Question 1. We draw a line segment PQ of length 5 cm. We take an external point A on the line segment. Let us draw a parallel line through point A to line segment PQ. [Let us draw three alternative processes].
Solution:
First method:
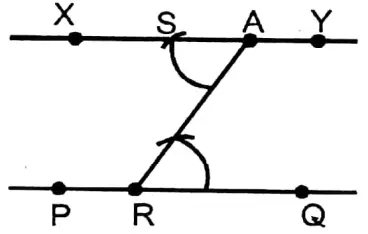
1. First draw a 5 cm long straight line PQ with the help of scale and outside PQ take any point.
2. On PQ straight line take any point R. A and R joined by scale, consequently is formed ∠ARQ. Now on point A on the opposite side of ∠ARQ ∠RAS joining is formed S and A by the scale and extending on both sides, got straight line XY
∴ ∠SAR = ∠ARQ, Alternate angles. XY II PQ
∴ XY is the required line through A and parallel to PQ.
Read and Learn More WBBSE Solutions For Class 9 Maths
Second Method:
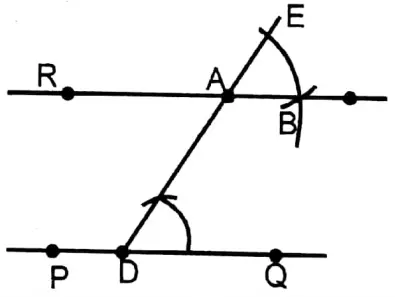
1. First draw a 5 cm long straight line PQ with help of scale and outside PQ take any point.
2. On PQ straight line takes any point D.
3. D and A are joined by scale.
DA is extended to point E, consequently, ∠ADQ is formed.
4. On the same side of AD, equal to ∠ADQ on straight line EA at point A, ∠EAB is formed.
5. BA straight line is extended to point R.
∴ ∠EAB = ∠ADQ (corresponding angles). ∵RB II PQ
RB is the required straight line through A and parallel to PQ.
Third Method:
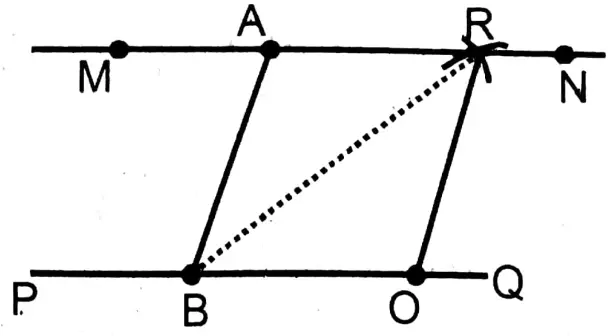
1. First draw a 5 cm long straight line PQ with the help of scale and outside PQ take any point
2. On PQ straight line take any point B. B and A are joined.
3. From BQ a segment BO is cut off.
4. Taking O as the centre, and taking a radius equal to BA, an arc is drawn.
5. Now taking A as a centre and taking a radius equal to BO another arc is drawn which cuts the former at point R. Joining A and R by the scale and extending on both sides we get MN straight line.
∴MN is the required straight line through A and parallel to PQ.
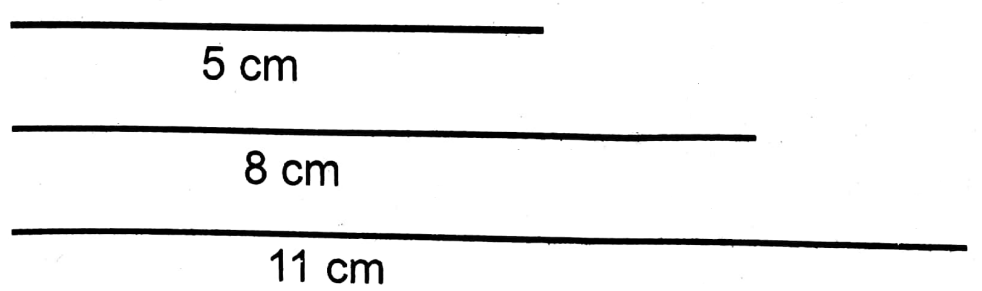
Question 2. We draw a triangle with lengths of sides 5 cm, 8 cm and 11 cm and draw a parallelogram equal in area to that triangle and having an angle of 60°. [Let us write instruction process and proof].
Solution:
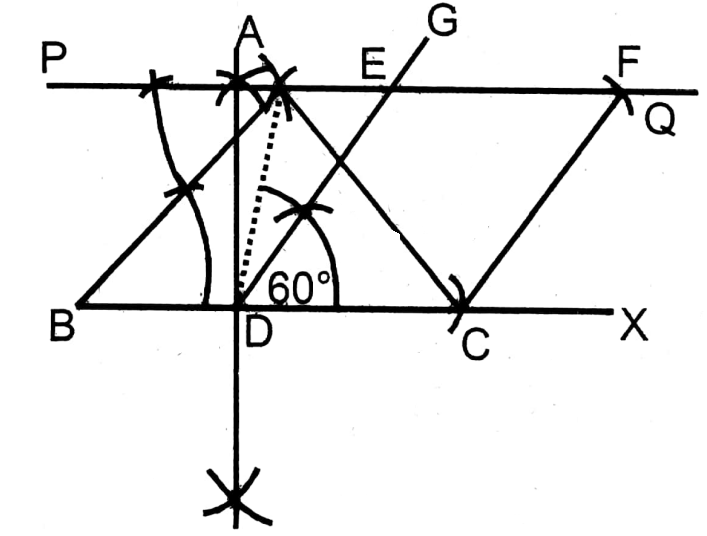
1. By scale, an 11 cm straight line BC is drawn. Taking B and C as centres, and taking radii equal to 8 cm and 5 cm respectively, two arcs are drawn which cut each other at point A. A B and AC are joined. ABC is a triangle whose sides AB = 8 cm, AC 5 cm and BC= 11 cm.
2. In the ΔABC side BC is bisected at point D.
3. In ΔABC from A to BC a parallel straight line PQ is drawn.
4. In ΔABC on side BC at point D an angle of 60°, ∠GDC is drawn which cuts PQ at E.
5. From EQ, DC equal to EF is cut and a joining C, F, and CDEF parallelogram is formed.
6. Proof: A, and D are joined.
In □EDCF, DC II EF (By construction) and DC EF (By construction)
∴ EDCF is a parattelogram.
ΔADC and parallelogram □EDCF are on the same base DC and between parallel lines DC and EF.
∴ ΔADC = \(\frac{1}{2}\) parallelogram □EDCF …..(1)
Again, in □ABC, AD is the median
∴ ΔADC = \(\frac{1}{2}\) ΔABC
From (1) and (2), ΔABC = parallelogram □EDCF
∴ Equal to ΔAABC in the area a parallelogram EDCF is formed whose one angle is 60°.
Question 3. We draw a triangle in which AB = 6cm, BC =9 cm, ∠ABC= 55°, let us draw a parallelogram equal in area to that triangle having an angle of 60° and length of one side is \(\frac{1}{2}\) of AC.
Solution:
1. A straight line AP is drawn in which segment AB equal to 6 cm is cut off. On point angle, ∠ABQ= 55° is drawn. From segment BQ, BC equal to 9 cm is cut off. A and C are joined; consequently ∠ABC is formed whose side AB = 6 cm, BC = 9 cm and <ABC = 55°
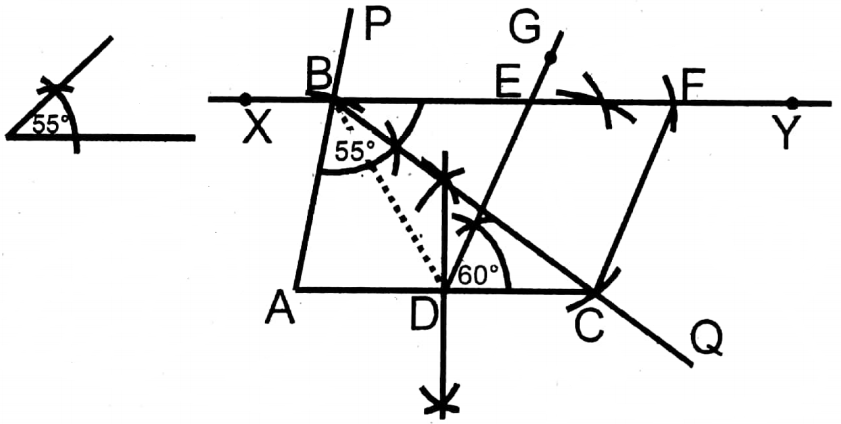
2. In ΔABC side AC is bisected at point D.
3. In ΔABC from point B parallel to AC an st. line XY is drawn.
4. In ΔABC on side AC at point D equal to 60° angle GDC is drawn which cuts XY at point E.
5. DC equal to EF is cut off from EY and joining C and F a parallelogram CDEF is formed.
Proof: B and D are joined.
In □CDEF, DC II EF (By construction) and DC = EF (By construction)
∴ CDEF is a parallelogram.
ΔBDC and parallelogram CDEF lie on same base DC and in between parallel lines DC and XY.
∴ ΔBDC = \(\frac{1}{2}\) parallelogram □CDEF
Again, in ΔABC, BD is the median
∴ ΔBDC = \(\frac{1}{2}\) ΔABC
∴ \(\frac{1}{2}\) ΔΑΒC = \(\frac{1}{2}\) parallelogram □CDEF
∴ ΔABC = parallelogram □ CDEF
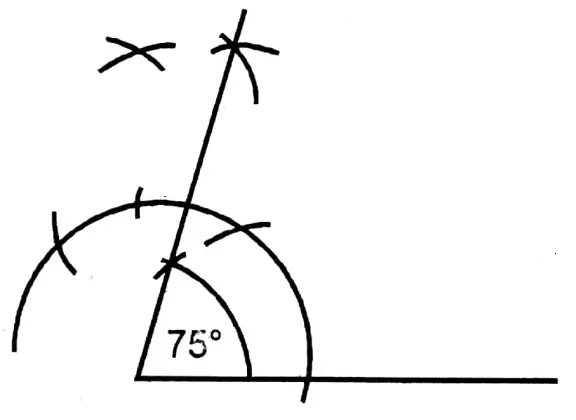
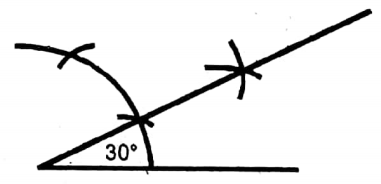
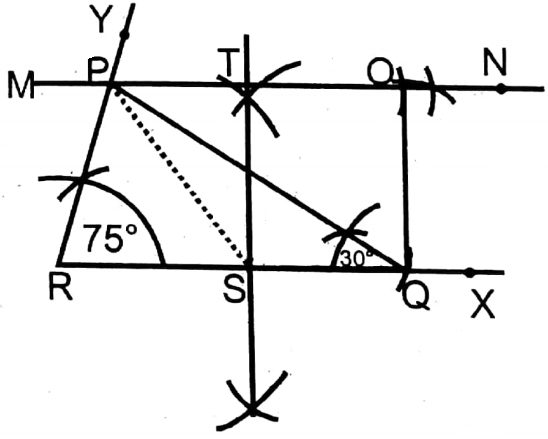
Question 4. In ΔPQR, ∠PQR = 30°, ∠PRQ = 75° and QR = 8 cm. Let us draw a rectangle equal in area to that triangle.
Solution:
1. PQR is a triangle whose ∠PQR = 30°, ∠PRQ = 75° and QR = 8 cm.
2. In ΔPQR from point P parallel to RQ a straight line MN is drawn.
3. RQ is bisected at S which cuts MN at T.
4. From TN equal to SQ segment TO is cut and O, and Q are joined. TSQO is the required rectangle.
Proof: P and S are joined.
In □TSQO, SQ II TO (By construction)
and SQ = TO (By construction)
and ∠TSQ = 90°
∴TSQO is a rectangle.
ΔPSQ and rectangle TSQO lie on the same base SQ and in between parallel lines SQ and PO.
∴ ΔPSQ= \(\frac{1}{2}\) rectangle TSQO
Again, in ΔPRQ, PS is the median
∴ ΔPSQ =\(\frac{1}{2}\) ΔPRQ
∴ \(\frac{1}{2}\) ΔPRQ= \(\frac{1}{2}\) rectangle TSQO
∴ PRQ rectangle TSQO Proved
Question 5. Draw an equilateral triangle with a length of each side of 6.5 cm and let us draw a parallelogram equal in area to that triangle and having an angle of 45°.
Solution:
Construction process:
1. An equilateral triangle AABC having a side 6 cm is drawn.
2. In ΔABC side BC is bisected at point D and from point A parallel to BC a straight line PQ is drawn.
3. In ΔABC at point D on side BC angle ∠EDC equal to 45° is drawn which cuts side PQ at point E.
4. Equal to DC EF is cut from the EQ segment. Joining C and F, the parallelogram CDEF is formed.
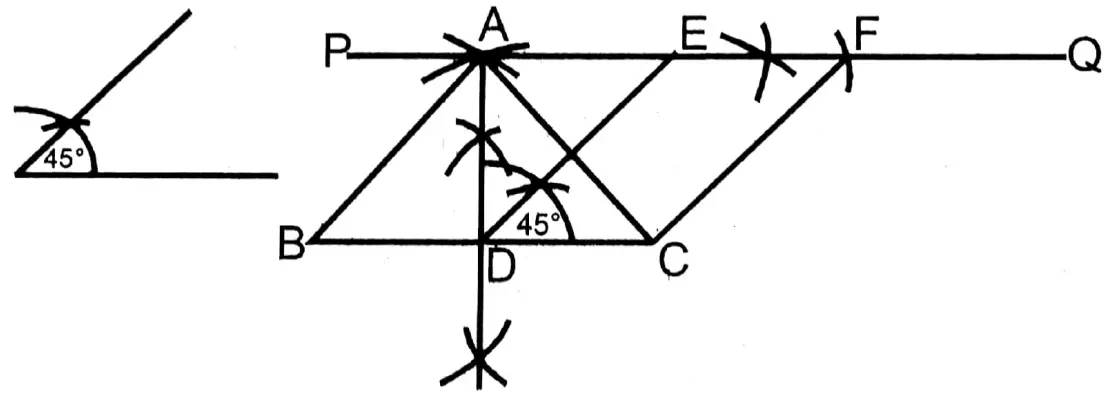
Proof: In □CDEF, DC II EF (By construction) and CD = EF (By construction)
∴ CDEF is a parallelogram.
ΔADC and parallelogram CDEF lie on the same base CD and in between parallel lines CD and AF.
∴ ΔADC = \(\frac{1}{2}\) parallelogram □CDEF
Again, in ΔABC, AD is the median
∴ΔADC = \(\frac{1}{2}\) ΔABC
∴ \(\frac{1}{2}\) ΔABC= \(\frac{1}{2}\) parallelogram □CDEF
∴ ΔABC = parallelogram □CDEF Proved
Question 6. The length of each equal side of an isosceles triangle is 8 cm and the length of the base is 5 cm. Let us draw a parallelogram equal in area to that circle and having one angle of a parallelogram is equal to one of the equal angles of an isosceles triangle and one side is \(\frac{1}{2}\) of equal side.
Solution: ABC, an isosceles triangle is formed whose base BC = 5 cm and equal sides AB = AC = 8 cm.
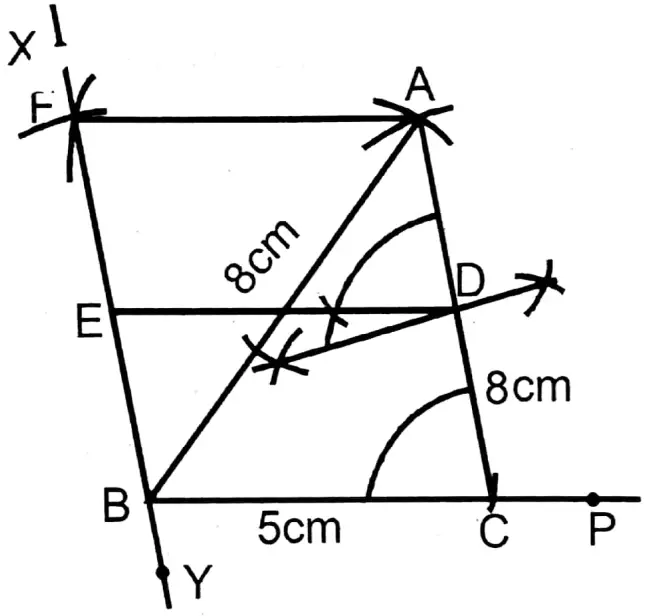
Equal to this triangle in area, a parallelogram ADEF is formed whose ∠D is equal to ∠C of the isosceles triangle.
Question 7. Construct an isosceles triangle whose equal sides are each equal to 8 cm and the vertical angle is 30°. Construct a parallelogram equal in area to this triangle.
Solution: ΔABC, an isosceles triangle is formed whose sides AB = AC = 8 cm and ΔBAC = 30°.
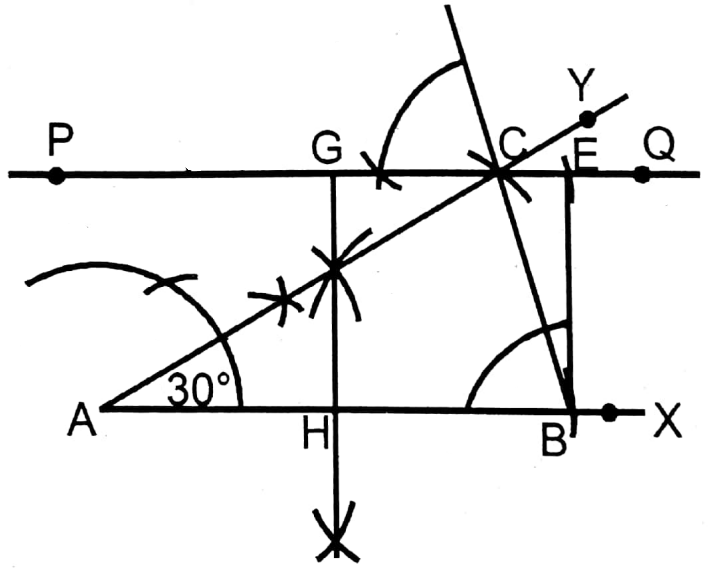
Equal to this triangle in the area is the parallelogram BEGH is formed.
