Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.1
Question 1. I see the house of Kamal and let us find the answer :
1. Let us write by calculating the area of Kamal’s garden.
2. Let us write by calculating how much cost is required to repair the floor of Kamal’s verandah.
3. Kamal wants to cover the floors of his reading room with tiles. Let us write by calculating how many tiles will be required to cover his floor of reading room with size of tiles 25 cm. x 25 cm.
Solution:
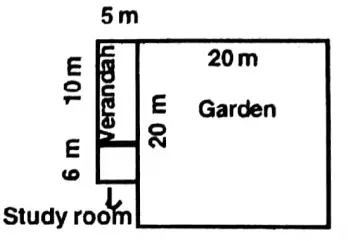
1. Area of Kamal’s garden = 20 x 20 sq.m = 400 sq.m
2. Area of verandah = 10 x 5 sq.m = 50 sq.m
Cost for repairing the floor of verandah = Rs. 50 x 30= Rs. 1500
3. Length of the reading room = 6 m = 600 cm
Breadth of the reading room = 5 m = 500 cm
Area of the reading room = 600 x 500 sq.cm
Area of each tile = 25 x 25 sq.cm
Read and Learn More WBBSE Solutions For Class 9 Maths
∴ No. of tiles = \(\frac{600 \times 500}{25 \times 25}=480\)
Question 2. Let us see the following pictures and calculate the area of its colored part.
Solution:
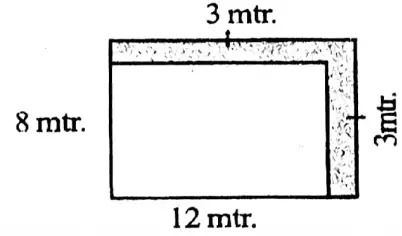
1. Length = 12 m
Breadth = 8 m
∴ Area = 12 x 8 sq.m = 96 sq.m
Length of the square except the colored part = (12 – 3) m = 9 m
Width of the square except the colored part = (8 – 3) m = 5 m
∴ Area of the square except coloured part = 9 x 5 sq.m = 45 sq.m
∴ Area of the colored part = (96-45) sq.m = 51 sq.m
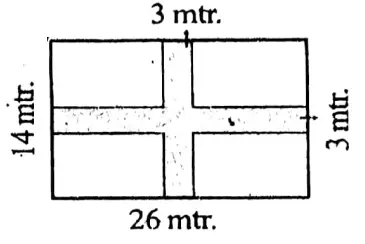
Wbbse Class 9 Maths Chapter 15.1 Area And Perimeter Solutions
2. Area of the coloured part = (26 x 3 + 14 x 3-3 x 3) sq.m = (78+ 429) sq.m
= (1209) sq.m = 111 sq.m
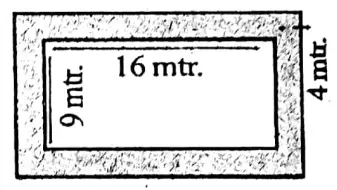
3. Length of the coloured part = (16+2 x 4) m = 24 m
Width of the coloured part = (9+ 2 × 4) m = 17 m
∴ Area of the rectangle including the colored part = (24 x 17) sq.m = 408 sq.m

Wbbse Class 9 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.1 Solutions
Length of the rectangle excluding the colored part = 16 mWidth of the rectangle excluding the colored part = 9 m
Area of the rectangle excluding the colored part 16 x 9 m = 144 sq.m
∴ Area of the coloured part = (408-144) sq.m = 264 sq.m
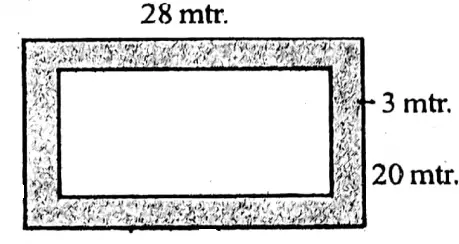
4. Area of the rectangle including the colored part = 28 x 20 sq.m = 560 sq.m
Area of the rectangle excluding the colored part = (28-2x 3) (20-2x 3) sq.m = 22 x 14 sq.m = 308 sq.m
∴ Area of the colored part of the rectangle = (560-308) sq.m = 252 sq.m
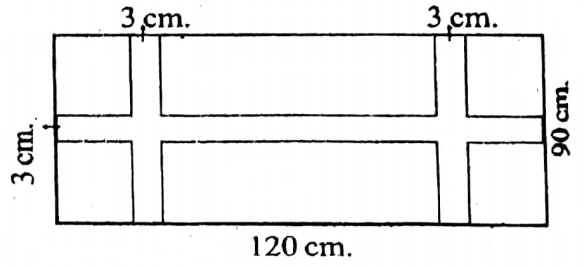
5. Area of the colored part of the rectangle = {120×3+90×3+90×3-(3×3)-(3×3)} sq.m
= (360+270 +270-9-9) sq.m
= (900-18) sq.m = 882 sq.m
Class 9 Wbbse Maths Area And Perimeter Exercise 15.1 Solved Problems
Question 3. The length and breadth of the rectangular field of Birati Mahajati Sangha are in the ratio 4: 3. The path of 336 meters is covered by walking once round the field. Let us write by calculating the area of the field.
Solution:
Given
The length and breadth of the rectangular field of Birati Mahajati Sangha are in the ratio 4: 3. The path of 336 meters is covered by walking once round the field.
Let the length & the breadth of the rectangular are 4x m & 3x m respectively.
∴ Perimeter of the rectangular field = 2x(Length + Breadth)
= 2(4x+3x) m = 14x m
According to the problem, 14x = 336
or, \(x=\frac{336}{14}\) = 24
∴ Length of the field = 4 x 24 m = 96 m
∴Breadth of the field= 3 x 24 m = 72 m
∴ Area of the field = Length x Breadth
= 96 × 72 sq.m
= 6912 sq.m
Question 4. The cost of farming a square land of Samar at the rate of Rs. 3.50 per sq. meter is Rs. 1,400. Let us calculate how much cost will be for fencing Samar’s land around its four sides with same height at the rate of Rs. 8.50 per meter.
Solution:
Given
The cost of farming a square land of Samar at the rate of Rs. 3.50 per sq. meter is Rs. 1,400.
Cost of farming a square at the rate of Rs. 3.50 per sq.m is Rs. 1400.
∴ Area of the square = \(\frac{1400}{3.50} \text { sq.m }\)
= \(\frac{1400 \times 100}{350} \text { sq.m }=400 \mathrm{sq} \cdot \mathrm{m}\)
∴ Length of each side of the square = √400 m = 20 m
Perimeter of the square = 4 x 20 m = 80 m.
∴ The cost for fencing the four sides of the square at the rate of Rs. 8.50 per meter 80 x Rs. 8.50 = Rs. 680.
Wbbse Class 9 Maths Chapter 15.1 Area And Perimeter Notes
Question 5. The area of the rectangular land of Suhas is 500 sq. meters. If the length of the land is decreased by 3 meters and the breadth is increased by 2 meters, then the land formed is a square. Let us write by calculating the length and breadth of the land of Suhas.
Solution:
Given
The area of the rectangular land of Suhas is 500 sq. meters. If the length of the land is decreased by 3 meters and the breadth is increased by 2 meters, then the land formed is a square.
Let the length of rectangular land = x m
∴ Breadth of the rectangular fland = \(\frac{500}{x} \mathrm{~m}\)
New length of the land = (x-3) m
& the new breadth of the land = \(\left(\frac{500}{x}+2\right) m\)
∵ Then the length will be equal to breadth.
∴ \(x-3=\frac{500}{x}+2\)
or, \(x-\frac{500}{x}=2+3\)
or, \(\frac{x^2-500}{x}=5\)
or, x2-500 = 5x
or, x2 -5x-500 = 0
or, x2 – (25-20)x-500 = 0
or, x2 -25x+20x-500 = 0
or, x(x-25)+20(x-25) = 0
or, (x-25)(x+20)=0
or, x+20=0
∴ X=-20
Length will never be negative.
∴ Length of the land is 25 m.
Breadth of the land = \(\frac{500}{25}\) m = 20 m.
Question 6. Each side of a square land of our village is 300 meters. We shall fence that square land by 3 dcm wide wall with the same height around its four sides. Let us see how much will it cost for the wall at the rate of Rs. 5,000 per 100 sq. nicer.
Solution:
Given
Each side of a square land of our village is 300 meters. We shall fence that square land by 3 dcm wide wall with the same height around its four sides.
Each side of the square = 300 m
Width of the wall = 3 dcm = \(\frac{3}{10}\) m = 0.3 m
Area of the land with wall = (300)2 sq.m
Area of the land without wall = (300-2x.3)2 sq.m (299.4)2 sq.m
Area of the wall = {(300)2– (299.4)2)} sq.m
= (300+299.4) (300-299.4) sq.m = 599.4 x 0.6 sq.m = 359.64 sq.m
∴ Cost of making 100 sq.m wall = Rs. 5000
∴ Cost of making 1 sq.m wall = \(\frac{5000}{100}\)
∴ Cost of making 359.64 sq.m wall = Rs. \(\frac{5000}{100}\) x 359.64 = Rs. 17982. 100
West Bengal Board Class 9 Area And Perimeter Exercise 15.1 Solutions
Question 7. The length and breadth of the rectangular garden of Rehana are 14 meters and 12 mars. If the cost of constructing an equally wide path inside the garden is Rs. 1,380 at the rate of Rs. 20 per sq. meter, then let us write by calculating how wide is the path.
Solution:
Given
The length and breadth of the rectangular garden of Rehana are 14 meters and 12 mars. If the cost of constructing an equally wide path inside the garden is Rs. 1,380 at the rate of Rs. 20 per sq. meter,
Length of the rectangle = 14m
The breadth of the rectangle = 12 m
Area of the garden including the path = 14 x 12 sq.m = 168 sq.m
Let the width of the path = x m
∴ Length of the garden without path = (14-2x)
Breadth of the garden without path = (12 -2x) m
Area of the garden without the path = (14-2x) (12-2x) sq.m
∵ Cost of constructing the path at the rate of Rs. 20 per sq.m = Rs. 138
∵ Area of the path = \(\frac{1380}{20}\) sq.m = 69 sq.m
According to the problem, 168- (14-2x) (12-2x) = 69
or, 168 (168-28x-24x+4x2) = 69
or, 168 (168-52x + 4x2) = 69
or, 168-168+52x-4x2-69=0.
or, – 4x2+52x-69 = 0
or, 4x2-52x + 69 = 0
or, 4x2-46x-6x+69 = 0
or, 2x(2×23)-3(2x-23) = 0
or, (2x-23) (2x-3)= 0
∴ Either (2x-23) or (2x-3) will be zero.
If 2x-23=0
∴ \(x=\frac{23}{2}\)
If 2x-3=0
∴ = \(\frac{3}{2}\)
Breadth of the path = 11.5 m
Length of garden without path = (14-2×11.5) m
= (14-23) m = -9m
∵ Length cannot be negative
∴ Breadth of the path = 1.5 m.
Wbbse Class 9 Area And Perimeter Of Triangle And Quadrilateral Important Questions Exercise 15.1
Question 8. If the length of a rectangular garden with area 1200 sq. cm is 40 cm. then let us write by calculating the area of square field which is drawn on its diagonal.
Solution: Area of the rectangular garden = 1200 sq.cm
Length of rectangular garden = 40 cm
∴ Width of the rectangular garden = Area/Length
= \(\frac{1200}{40} \mathrm{~cm}=30 \mathrm{~cm}\)
Diagonal of the rectangular garden = \(\sqrt{(\text { length })^2+(\text { width })^2}\)
\(\begin{aligned}& =\sqrt{(40)^2+(30)^2} \mathrm{~cm} \\
& =\sqrt{1600+900} \mathrm{~cm} \\
& =\sqrt{2500} \mathrm{~cm} \\
& =50 \mathrm{~cm}
\end{aligned}\)
Each side of the square drawn on the diagonal of the rectangular garden = 50 cm.
∴ Area of the square =(50)2 sq.cm = 2500 sq.cm.
Question 9. The length, breadth, and height of a hall are 4 meters, 6 meters, and 4 meters. There are three doors and four windows in the room. The measurement of each door is 1.5 meters x 1 meter and each window is 1.2 meters x 1 meter. How much will it cost for covering four walls by colored paper at the rate of Rs. 70 per square meter?
Solution:
Given
The length, breadth, and height of a hall are 4 meters, 6 meters, and 4 meters. There are three doors and four windows in the room. The measurement of each door is 1.5 meters x 1 meter and each window is 1.2 meters x 1 meter.
Area of the 4 walls of a room = 2x( L + B) xh
= 2(4+6) x 4 sq.m = 80 sq.m
Area of 3 doors and 4 windows
=(3x 1.5 x 14 x 1.2 x 1) sq.m
= (4.5+ 4.8) sq.m
= 9.3 sq.m
Area of the walls excluding the areas
= (80-9.3) sq.m
= 70.7 sq.m
Cost of covering colored papers on the walls at the rate of Rs. 70 per sq.m Rs. 70 x 70.7 = Rs. 4949.
Question 10. The area of four walls of a room is 42 sq. meters and area of the floor is 12 sq. meters. Let us write by calculating the height of the room if the length of the room is 4 meter.
Solution:
Given
The area of four walls of a room is 42 sq. meters and area of the floor is 12 sq. meters.
Area of floor of the room = 12 sq.m
Length of the room = 4 m
∴ Breadth of the room = \(\frac{12}{4}\) m = 3m
Let the height of the room = x m.
∴ Area of 4 walls of the room
= 2(4+3) x x sq.m = 14x sq.m
According to the problem, 14x = 42
or, x = \(\frac{42}{14}\)
∴ Height of the room = 3 m
Question 11. Sujata will draw a rectangular picture on paper with area of 84 sq. cm. The difference between the length and breadth of the paper is 5 cm. Let us calculate the perimeter of paper of Sujata.
Solution:
Given
Sujata will draw a rectangular picture on paper with area of 84 sq. cm. The difference between the length and breadth of the paper is 5 cm.
Length of the paper = x cm
∴ Breadth of the paper = (x-5) cm
∴Area of the paper = LXB
= x(x-5) sq.cm
= x2 – 5x sq.cm
According to the problem,
x2 – 5x = 84
or, x2 -5x-84 = 0
or, x2 – 12x+7x-84 = 0
or, x(x-12)+7(x-12)=0
or, (x-12) (x+7)=0
Either (x-12) or (x+7) will be equal to zero.
If x-12=0
∴ x = 12
or, If x+7=0
∴ X=-7
∵ Length of paper will not be zero.
∴ Length of the room = 12 cm
Breadth of the room = (12-5) cm = 7 cm
Perimeter of the paper = 2(L+B)
= 2(12+7) cm
= 2 x 19 cm
= 38 cm.
Wbbse Class 9 Maths Area And Perimeter Exercise 15.1
Question 12. There is a 2.5-meter wide path around the square garden of Shiraj’s. The area of path is 165 sq meters. Let us calculate the area of the garden and the length of diagonal. (√2-1.414)
Solution:
Given
There is a 2.5-meter wide path around the square garden of Shiraj’s. The area of path is 165 sq meters.
Let each side of the square garden = x m.
∴ Area of the garden = x2 sq.m
Length of side with the path = (x + 2 x 2.5) m = (x+5) m
Area of the garden with the path = (x+5)2 sq.m
∴ Area of the path = {(x+5)2-x2} sq.m
According to the problem, (x+5)2 – x2 = 165
or, x2+10x + 25-x2 = 165
or, 10x 165-25
or, 10x = 140
or, x = \(\frac{140}{10}\) = 14
∴ Length of each side of the square = 14 m
∴ Area of the garden = (14)2 sq.m 196 sq.m
Length of the diagonal = √2×14 m
= 1.414 x 14 m
= 19.796 m.
Question 13. Let us write by calculating how much length of wall in meter is required for walling outside round the square field, whereas the length of diagonal of the square land is 20√2 meter. Let us write by calculating how much cost will be incurred for planting grass at the rate of Rs. 20 per sq. meter.
Solution: Length of the diagonal of the square field = 20√2 m
Length of one side of the square field = \(\frac{\text { Diagnal }}{\sqrt{2}}=\frac{20 \sqrt{2}}{\sqrt{2}} \mathrm{~m}=20 \mathrm{~m}\)
Perimeter of the field = 4 x 20 m= 80m
Area of the field = (20)2 sq.m
=400sq.m
= Rs.400x 20 = Rs. 8000
Wbbse 9th Class Maths Area And Perimeter Exercise 15.1 Step By Step Solutions
Question 14. We shall fence our rectangular garden diagonally. The length and breadth of the rectangular garden are 12 meters and 7 meters. Let us calculate the length of the fence.
Solution:
Given
We shall fence our rectangular garden diagonally. The length and breadth of the rectangular garden are 12 meters and 7 meters.
Length of the diagonal of the garden
\(\begin{aligned}& =\sqrt{(\text { length })^2+(\text { breadth })^2} \\
& =\sqrt{(12)^2+(7)^2} \mathrm{~m} \\
& =\sqrt{144+49} \mathrm{~m} \\
& =\sqrt{193} \mathrm{~m}
\end{aligned}\)
∴ Length of fence = √193 m
or, Perimeter of the triangle formed by the diagonal of the rectangle
=(12+7+√193) m = (19+ √193) m
Question 15. The big hall of house of Mousumi is in the form of a rectangle, of which length and breadth are in the ratio 9: 5 and the perimeter is 140 meters. Mousmi wants to cover the floor of her hall with rectangular tiles of dimensions 25 cm x 20 cm. The rate of each 100 tiles is Rs. 500. Let us calculate the cost for covering the floor with tiles.
Solution:
Given
The big hall of house of Mousumi is in the form of a rectangle, of which length and breadth are in the ratio 9: 5 and the perimeter is 140 meters. Mousmi wants to cover the floor of her hall with rectangular tiles of dimensions 25 cm x 20 cm. The rate of each 100 tiles is Rs. 500.
Let the length & breadth of the floor are 9x m and 5x m respectively.
∴ Perimeter = 2(L+B)
= 2(9x+5x) m
= 2 x 14x m = 28x m
According to the problem, 28x=140
or, x = \(x=\frac{140}{28}\)
∴ Length of the hall = 9x 5 m = 45 m
= 45 x 100 cm = 4500 cm
Breadth of the hall = 5 x 5 m = 25 m
= 25 x 100 cm 2500 cm
Area of the hall = 4500 x 2500 sq.cm
Area of each tile = 25 cm x 20 cm
∴ Number of tiles = 4500 x 2500 25×20 = 22500
∴ Cost of 100 tiles = Rs. 500
∴ Cost of 1 tile = Rs. \(\frac{500}{100}\) = Rs. 5
∴ Cost of 22500 tiles = Rs. 22500 x 5 = Rs. 112500
∴ Cost for covering the floor with tiles = Rs. 112500.
Wbbse Class 9 Maths Area And Perimeter Formulas With Examples Exercise 15.1
Question 16. The cost of carpeting a big hall of length 18 meters is Rs. 2160. If the breadth of the floor would be 4 meters less, then the cost would have been Rs. 1,620. Let us calculate the perimeter and area of the hall.
Solution:
Given
The cost of carpeting a big hall of length 18 meters is Rs. 2160. If the breadth of the floor would be 4 meters less, then the cost would have been Rs. 1,620.
If the breadth is 4 m less, cost will decrease = Rs. (2160-1620) = Rs. 540
∴ If the breadth is 1 m less, cost will decrease = Rs. \(\frac{540}{4}\) = Rs. 135
∵ Cost of 1 m carpet is Rs. 135, i.e., Rs. 135 is the cost of 1 m carpet.
∴ Re. 1 is cost of \(\frac{1}{135}\) m carpet.
∴ Rs. 2160 is the cost of \(\frac{1}{135} \times 2160\) m carpet.
∴ Rs. 2160 is the cost of 6 m carpet.
∵ The breadth of the room = 16 m
∵ Length of the room = 18 m
∴ Area of the hall = 18 x 16 sq.m = 288 sq.m.
Question 17. The length of the diagonal of a rectangular land is 15 meter and the difference of length and breadth is 3 meters. Let us calculate the perimeter and area.
Solution:
Given
The length of the diagonal of a rectangular land is 15 meter and the difference of length and breadth is 3 meters.
Let the breadth of the rectangular land = xm
∴ Length of the land = (x + 3) m
∴ Length of the diagonal of the land = \(\sqrt{(x+3)^2+(x)^2} m\)
\(\begin{aligned}& =\sqrt{x^2+6 x+9+x^2} m \\
& =\sqrt{2 x^2+6 x+9} \mathrm{~m}
\end{aligned}\)
According to the problem,
\(\begin{aligned}& \sqrt{2 x^2+6 x+9}=15 \\
& \text { or, }\left(\sqrt{2 x^2+6 x+9}\right)^2=(15)^2
\end{aligned}\)
or, 2x2+6x+9=225
or, 2x2+6x+9-225 = 0
or, 2x2+6x-216=0
or, 2(x2+3x-108) = 0
or,x2+3x-108 = 0
or,x2 + 12x-9x-108=0
or, x(x+12)-9(x+12)=0.
or, (x+12) (x-9)=0
Either, x+12= 0 or x-9=0
If x + 12 = 0
∴ X=-12
or, If x-9=0
∴ X=9
As the breadth will not be negative,
∴ Breadth of the rectangular land = 9m
∴ Length of the rectangular land = (9+3) m = 12 m
Perimeter of the land = 2(L + B)
= 2(12+9) m = 42 m
Area of the land = L x B
= 12 x 9 sq.m = 108 sq.m.
Class 9 Wbbse Area And Perimeter Of Triangle And Quadrilateral Exercise 15.1 Solved Exercises
Question 18. Let us calculate what is the longest size of the square tile that can be used for paving the rectangular courtyard with measurement of 385 meter x 60 meter and also find the number of tiles.
Solution: As the tiles are square shaped
∴ Length of the side of the square tiles is the H.C.F of 385 m & 60m = 5 m.
∴ For paving the rectangular courtyard with square tiles whose maximum size is 5 m. sq. Area of each tiles =(5)2 sq.m = 25 sq.m
∴ Number of tiles = \(\frac{385 \times 60}{25}\) = 924
Question 19. Multiple choice questions
1. The length of diagonal of square is 12√2 cm. The area of the square is
1. 288 sq. cm.
2. 144 m2
3. 72 m2
4. 18 m2
Solution: Diagonal of the square= 12√2 cm
∴ Area of the square = \(=\frac{1}{2} \times(12 \sqrt{2})^2 \text { sq.cm }\)
= \(\frac{1}{2} \times 144 \times 2 \text { sq.cm }\)
= 144 sq. cm
∴ 2. 144 sq. cm
2. If the area of square is A1 sq. units and the area of the square drawn on the diagonal of the square is A2 sq. unit, then the ratio of A1 : A2 is
1. 1:2
2. 2:1
3.1:4
4. 4:1
Solution: Let the length of one side of the square = x unit
∴ Area of the square = (A1) = x2 sq.unit
Length of the diagonal = √2x unit
∴Area of the square drawn on the diagonal of the square = ( A2) = (√2x)2 sq.unit = 2 x2sq.unit
∴ A1: A2 = x2: 2×2
∴ 1. 1:2
3. If a rectangular place of which length and breadth are 6 meter and 4 meter, is desired to pave it with 2 cm square tiles, then the number of tiles is required are
1. 1200
2. 2400
3. 600
4. 1800
Solution: Length of rectangular land = 6 m x 10 d.cm = 60 d.cm
Breadth of the rectangular land = 4 m x 10 d.cm = 40 d.cm
∴ Area of the rectangular land = 60 × 40 sq d.cm
Area of one tile =(2)2 sq d.cm = 4 sq d.cm
∴ Number of tiles \(=\frac{\text { Area of the rectangular land }}{\text { Area of each tile }}\)
= \(\frac{60 \times 40}{4}=600\)
∴ 3. 600
4. If a square and a rectangle have the same perimeter and their areas are S and R respectively then
1. S = R
2. S>R
3. S<R
4. None of these
Solution: Between the square & a rectangle of same perimeter, area of the square is greater than the area of the rectangle.
∴ 2. S> R
5. If the length of the diagonal of a rectangle is 10 cm and area is 62.5 sq. cm, then the sum of their length and breadth is
1. 12 cm.
2. 15 cm
3. 20 cm
4. 25 cm
Solution:
Given
If the length of the diagonal of a rectangle is 10 cm and area is 62.5 sq. cm
Let the length and breadth of a rectangle are x cm & y cm respectively.
∴ Length of the diagonal of the rectangle = \(\sqrt{x^2+y^2} \mathrm{~cm}\) cm
∴ Area of the rectangle = xy sq. cm
According to 1st condition, \(\sqrt{x^2+y^2}=10\)
or, \(\left(\sqrt{x^2+y^2}\right)^2=(10)^2\) (Squaring both sides)
or, x2 + y2= 100 …(1)
According to 2nd condition,
xy = 62.5
∴ 2xy=2x 62.5 (multiplying both sides by 2)
or, 2xy = 125 …(2)
Adding (1) & (2),
x2 + y2+ 2xy = 100 + 125
or, (x + y)2 = 225
or, x+y= √√225
or, x + y = 15
∴ Sum of the length and breadth of the rectangle = 15 cm.
∴ 2. 15 cm.
Question 20. Short answer type questions
1. If the length of square is increased by 10%, then what percent of area of the square will be increased?
Solution:
Given
If the length of square is increased by 10%,
Let each side of the square = x unit
∴ Area of the square = x2 sq.unit.
Increasing 10% of each side of the square = x 10% = \(\frac{x \times 10}{100} \text { unit }=\frac{x}{10} \text { unit }\)
∴ New length of each side of the square = \(\left(x+\frac{x}{10}\right) \text { unit }=\frac{11 x}{10} \text { unit }\)
Area of new square= \(\left(\frac{11 x}{10}\right)^2 \text { sq.unit }=\frac{121 x^2}{100} \text { sq.unit }\)
Increase in area = \(\left(\frac{121 x^2}{100}-x^2\right) \text { sq.unit }\)
\(\begin{aligned}
& =\frac{121 x^2-100 x^2}{100} \text { sq.unit } \\
& =\frac{21 x^2}{100} \text { sq.unit }
\end{aligned}\)
Percentage increase in area = \(\frac{21 x^2}{100} \times \frac{100}{x^2}=21 \%\)
2. If the length is increased by 10% and the breadth is decreased by 10% of a rectangle, then what percent of area will be increased or decreased?
Solution:
Given
If the length is increased by 10% and the breadth is decreased by 10% of a rectangle
Let the length & breadth of a rectangle are x unit & y unit respectively.
∴ Area of the rectangle = xy sq.unit
Length is increased by 10% = x + 10% of x.
= \(\left(x+\frac{10 x}{100}\right) \text { unit }=\frac{11 x}{10} \text { unit }\)
Breadth is decreased by 10% = \(\left(y-\frac{10 y}{100}\right) \text { unit }=\frac{9 y}{10} \text { unit }\)
∴ New area of this rectangle = \(\frac{11 x}{10} \times \frac{9 x}{10} \text { sq.unit }\)
∴ Decrease in area = \(\left(x y-\frac{99 x y}{100}\right) \text { sq.unit }\)
= \(\frac{x y}{100} \text { sq.unit }\)
∴ Percentage decrease in area = \(\frac{x y}{100} \times \frac{100}{x y}=1 \%\)
3. The length of a rectangle is 5 cm. The length of the perpendicular on the breadth of the rectangle from an intersecting point between two diagonals is 2 cm. What are the length and breadth?
Solution:
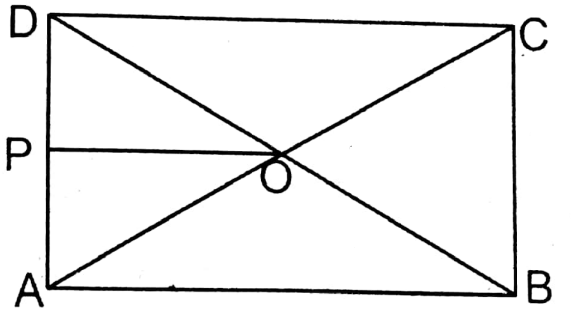
Given
The length of a rectangle is 5 cm. The length of the perpendicular on the breadth of the rectangle from an intersecting point between two diagonals is 2 cm.
Let diagonals AC & BD of the rectangle ABCD intersect at O. OP is the perpendicular drawn from O on AD; OP = 2 cm.
∴ Length of the rectangle = (AB) = 2 × OP = 2x 2 cm 4 cm
ΔABC is a right-angled triangle whose ∠B is a right angle ( ABCD is a rectangle) From the Pythagoras theorem,
AC2 = AB2 + BC2
or, (5)2 = (4)2 + BC2
or, 25 -16 BC2
or, 9 = BC2
or, BC2 = 9
or, BC = +3
As the breadth is not negative,
∴BC = 3 cm
∴ Breadth of the rectangle = 3 cm.
4. If the length of the perpendicular from the intersecting point between two diagonals on any side of square is 2√2 cm, then what is the length of each diagonal or square?
Solution:
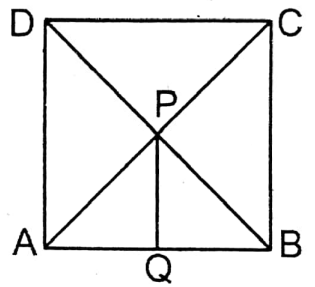
Given
If the length of the perpendicular from the intersecting point between two diagonals on any side of square is 2√2 cm,
Let the diagonals AC & BD of the square ABCD intersect at P. PQ is the perpendicular from P on AB.
∴ PQ = 2√2 cm
∴ Length of each side of square = 2×2√2 cm = 4√2 cm
∴ Length of each diagonal of square = √2 × side = √2×4√2 cm = 8 cm.
5. The perimeter of a rectangle is 34 cm and its area is 60 sq. cm. What is the length of each diagonal?
Solution: Let the length and breadth of a rectangular are x cm & y cm respectively.
∴ Perimeter of the rectangle = 2(x + y) cm
& Area of the rectangle = xy sq.cm
According to 1st,condition, 2(x+y)=34
or, x + y = \(\frac{34}{2}\)
or, x + y = 17.
According to 2nd condition, xy = 60
From equation (1), x + y = 17 …(2)
or, (x + y)2=(17)2 (Squaring both sides)
or, (x-y)2 + 4xy = 289
or, (x-y)2+4 x 60 = 289
or, (x-y)2+240 = 289
or, (x-y)2 = 289-240
or, (x-y)2 = 49
or, x – y = √49
or, x – y = 7 …(2)
Adding (1) & (2),
2x = 24
or, \(x=\frac{24}{2}=12\)
Putting the value of x in equation (1),
12+y=17
or, y = 17-12=5
Length of the rectangle 12 cm & breadth = 5 cm
Length of the diagonal of the rectangle = \(\sqrt{(12)^2+(5)^2} \mathrm{~cm}\)
\(\begin{aligned}
& =\sqrt{144+25} \mathrm{~cm} \\
& =\sqrt{169} \mathrm{~cm} \\
& =13 \mathrm{~cm}
\end{aligned}\)
