Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.2
Question 1. Let us write by calculating the area of the following regions:
Solution:
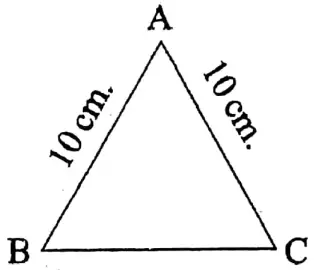
1. In the Image it is an equilateral triangle whose each side = 10 cm.
∴ Area of ΔABC = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)
\(\begin{aligned}& =\frac{\sqrt{3}}{4} \times(10)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{1} \times 100 \text { sq.cm }=25 \sqrt{3} \text { sq.cm }
\end{aligned}\)
Read and Learn More WBBSE Solutions For Class 9 Maths
Wbbse Class 9 Maths Chapter 15.2 Area And Perimeter Solutions
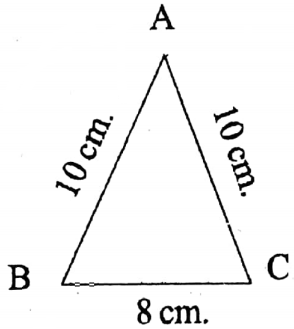
2. In the 2nd image it is an isosceles triangle whose equal sides are 10 cm each and the base = 8 cm.
∴ Area of ΔABC = \(=\frac{1}{2} \cdot 8 \sqrt{(10)^2-\frac{(8)^2}{4}} \text { sq.cm }\)
\(\begin{aligned}& =4 \sqrt{100-16} \text { sq.cm } \\
& =4 \sqrt{84} \text { sq.cm } \\
& =4 \sqrt{2 \times 2 \times 21} \text { sq.cm } \\
& =4.2 \sqrt{21} \text { sq.cm } \\
& =8 \sqrt{21} \text { sq.cm. }
\end{aligned}\)
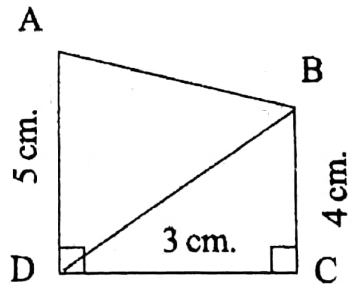
3. In the 3rd image in ABCD, ∠ADC= ∠BCD = 90°
∴ AD II BC
∴ ABCD is a trapezium.

Wbbse Class 9 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.2 Solutions
∴ Area of ABCD = \(\frac{1}{2}\) (4+5)x3 sq.cm
=\( \frac{1}{2}\) x27 sq.cm
= 13.5 sq.cm.
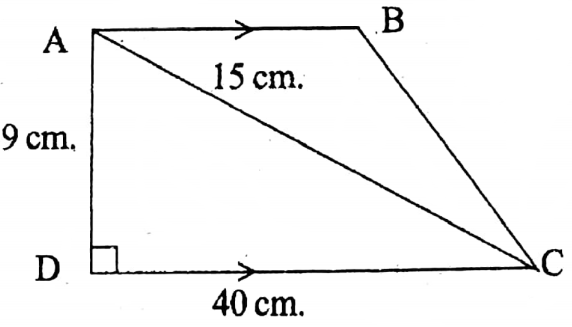
4. In the 4th image ABCD is a trapezium.
∴ Area of ABCD = \(\frac{1}{2}\)(40+15)×9 sq.cm
= \(\frac{1}{2}\) x55x9 sq.cm
= \(\frac{495}{2}\)
= 247.5 sq. cm.
Class 9 Wbbse Maths Area And Perimeter Exercise 15.2 Solved Problems
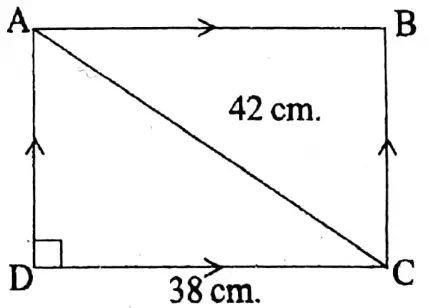
5. In 5th image ABCD is a rectangle whose length = 38 cm & diagonal (AC)= 42 cm.
In ΔADC, AD = \(\sqrt{A C^2-C D^2}\)
\(\begin{aligned}& =\sqrt{(42)^2-(38)^2} \mathrm{~cm} \\
& =\sqrt{(42+38)(42-38)} \mathrm{cm} \\
& =\sqrt{80 \times 4} \mathrm{~cm} \\
& =8 \sqrt{5} \mathrm{~cm} .
\end{aligned}\)
∴ Area of ABCD = ABX AD
= 38×8√5 sq.cm
=304√5 sq.cm.
Question 2. The perimeter of any equilateral triangle is 48 cm. Let us write by calculating its area.
Solution:
Given
The perimeter of any equilateral triangle is 48 cm.
Length of each side of the equilateral triangle = \(\frac{48}{3} \cdot \mathrm{cm}=16 \mathrm{~cm}\)
Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)
\(\begin{aligned}& =\frac{\sqrt{3}}{4} \times(16)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 256 \text { sq.cm } \\
& =64 \sqrt{3} \text { sq.cm }
\end{aligned}\)
Question 3. If the height of an equilateral triangle ABC is 5√3 cm, let us write by calculating the area of this triangle.
Solution:
Given
If the height of an equilateral triangle ABC is 5√3 cm
Height of an equilateral triangle = \(\frac{\sqrt{3}}{2} \times \text { side }\)
∴ Each side of an equilateral triangle = \(\frac{2}{\sqrt{3}} \times \text { height }\)
= \(\frac{2}{\sqrt{3}} \times 5 \sqrt{3} \mathrm{~cm}=10 \mathrm{~cm}\)
∴ Perimeter of the equilateral triangle = 3 x 10 cm 30 cm
Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { angle })^2\)
\(\begin{aligned}& =\frac{\sqrt{3}}{4} \times(10)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 100 \text { sq.cm } \\
& =25 \sqrt{3} \text { sq.cm. }
\end{aligned}\)
Wbbse Class 9 Maths Chapter 15.2 Area And Perimeter Notes
Question 4. If each equal side of an isosceles triangle ABC is 10 cm and length of base is 4 cm, let us write by calculating the area of ΔABC.
Solution:
Given
If each equal side of an isosceles triangle ABC is 10 cm and length of base is 4 cm
Area ΔABC = \(\frac{1}{2} \cdot 4 \cdot \sqrt{(10)^2-\frac{(4)^2}{4}} \text { sq.cm }\)
\(\begin{aligned}& =2 \sqrt{100-4} \text { sq.cm } \\
& =2 \sqrt{96} \text { sq.cm } \\
& =2 \sqrt{4 \times 4 \times 6} \text { sq.cm } \\
& =8 \sqrt{6} \text { sq.cm. }
\end{aligned}\)
Question 5. If length of base of any isosceles triangle is 12 cm and length of each equal side is 10 cm, let us write by calculating the area of that isosceles triangle.
Solution:
Given
If length of base of any isosceles triangle is 12 cm and length of each equal side is 10 cm
Area of the isosceles triangle = \(\frac{1}{2} \cdot 12 \sqrt{(10)^2-\frac{(12)^2}{4}} \text { sq. cm }\)
\(\begin{aligned}& =6 \cdot \sqrt{100-36} \text { sq. } \mathrm{cm} \\
& =6 \cdot \sqrt{64} \text { sq. } \mathrm{cm} \\
& =6 \times 8 \text { sq. } \mathrm{cm}=48 \mathrm{sq} . \mathrm{cm}
\end{aligned}\)
Question 6. The perimeter of any isosceles triangle is 544 cm and the length of each equal side is \(\frac{5}{6}\) th of length of base. Let us write by calculating the area of this triangle.
Solution:
Given
The perimeter of any isosceles triangle is 544 cm and the length of each equal side is \(\frac{5}{6}\) th of length of base.
Let the base of an isosceles triangle = x cm.
∴ Length of each equal side of the isosceles triangle = \(\frac{5 x}{6}\) cm
∴ Perimeter of the triangle = \(\left(x+\frac{5 x}{6}+\frac{5 x}{6}\right) \mathrm{cm}\)
\(\begin{aligned}& =\frac{6 x+5 x+5 x}{6} \mathrm{~cm} \\
& =\frac{16 x}{6} \mathrm{~cm}=\frac{8 x}{3} \mathrm{~cm}
\end{aligned}\)
According to the problem, \(\frac{8 x}{3}=544\)
or, \(x=\frac{544 \times 3}{8}=204\)
∴ Length of the base of the isosceles triangle = 204 cm.
Length of each equal side of the triangle= \(\frac{5}{6}\) x 204 cm = 170 cm.
∴ Area of the isosceles triangle = \(\frac{1}{2} \times 204 \sqrt{(170)^2-\frac{(204)^2}{4}} \text { sq.cm }\)
\(\begin{aligned}& =102 \sqrt{(170)^2-(102)^2} \text { sq. cm } \\
& =102 \sqrt{(170+102)(170-102)} \text { sq. cm } \\
& =102 \sqrt{272 \times 68} \text { sq. cm } \\
& =102 \sqrt{4 \times 68 \times 38} \text { sq. cm }
\end{aligned}\)
= 102 x 2 x 68 sq. cm
= 13872 sq. cm.
Question 7. If the length of hypotenuse of an isosceles right-angled triangle is 12√2 cm, let us write by calculating the area of this triangle.
Solution:
Given
If the length of hypotenuse of an isosceles right-angled triangle is 12√2 cm,
Let each equal side of the right angled isosecles triangle = x cm.
Length of the hypotenuse of the triangle = \(\begin{aligned}
& \sqrt{x^2+x^2} \mathrm{~cm} \\
& \sqrt{2 x^2} \mathrm{~cm} \\
& x \sqrt{2} \mathrm{~cm}
\end{aligned}\)
According to the problem,
\(x \sqrt{2}=12 \sqrt{2}
or, x=\frac{12 \sqrt{2}}{\sqrt{2}}
or, x=12 \)
∴Length of each equal side of the right-angled isosecles triangle = 12 cm.
∴ Area of the triangle = \(\frac{1}{2}\) x 12×12 sq. cm = 72 sq. cm.
West Bengal Board Class 9 Area And Perimeter Exercise 15.2 Solutions
Question 8. Pritha drew a parallelogram of which lengths of two diagonals are 6 cm and 8 cm and each angle between two diagonals is 90°. Let us write the length of sides of the parallelogram and what type of parallelogram it is.
Solution:
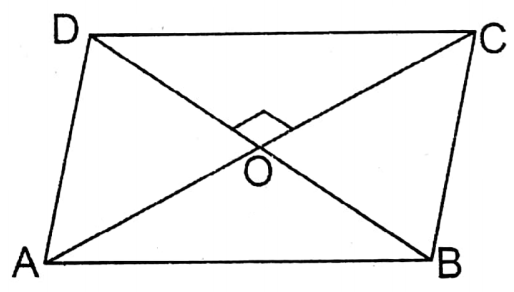
Given
Pritha drew a parallelogram of which lengths of two diagonals are 6 cm and 8 cm and each angle between two diagonals is 90°.
Let the diagonals AC & BD of the parallelogram ABCD intersect each other at O.
And AC = 8 cm; BD = 6 cm
According to the problem,
∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
We know if the diagonals of a parallelogram bisect each other at right angles, it will be a rhombus.
∴ ABCD is a rhombus.
\(\begin{aligned}& therefore O C=\frac{1}{2} A C=\frac{1}{2} \times 8 \mathrm{~cm}=4 \mathrm{~cm} \\
& \& O D=\frac{1}{2} B D=\frac{1}{2} \times 6 \mathrm{~cm}=3 \mathrm{~cm}
\end{aligned}\)
In right angled ΔCOD,
CD2 = OC2+ OD2
or, CD2=(4)2+ (3)2
or, CD2= 16+9
or, CD2 = 25
or, CD = √25=5
Each side of the rhombus is equal.
∴ AB = BC = CD = DA = 5 cm
∴ Parallelogram ABCD is a rhombus.
Question 9. The ratio of the lengths of sides of a triangular park of our village is 2:3: 4; perimeter of park is 216 meters.
1. Let us write by calculating the area of the park.
2. Let us write by calculating how long is to be walked from oppositevertex of the longest side to that side straightly.
Solution:
Given
The ratio of the lengths of sides of a triangular park of our village is 2:3: 4
Let the sides of a triangular park are = 2x m 3x m, & 4x m
∴ Perimeter of the park = (2x + 3x + 4x) m = 9x m
According to the problem,
9x = 216
or, x = \(\frac{216}{9}\) = 24
∴ One side of the park = 2 x 24 m = 48 m
∴ 2nd side of the park = 3 x 24 m = 72 m
∴ 3rd side ut the park = 4 x 24 m = 96 m
Semi-perimeter of the park = \(\frac{216}{2} \mathrm{~m}\) = 108 m
1. Area of the park = \(\sqrt{108(108-48)(108-72)(108-96)} \text { sq.m }\)
\(\begin{aligned}& =\sqrt{108 \times 60 \times 36 \times 12} \text { sq.m } \\
& =\sqrt{3 \times 36 \times 3 \times 4 \times 5 \times 36 \times 3 \times 4} \text { sq.m } \\
& =3 \times 36 \times 4 \sqrt{3 \times 5} \text { sq.m } \\
& =432 \sqrt{15} \text { sq.m }
\end{aligned}\)
2. Perpendicular distance from the opposite vertex to the biggest side
\(\begin{aligned}& =\frac{2 \times \text { Area of the park }}{\text { Length of the longest side }} \\
& =\frac{2 \times 432 \sqrt{15}}{96} \mathrm{~m} \\
& =9 \sqrt{15} \mathrm{~m}
\end{aligned}\)
∴ Distance to be walked from the opposite vertex to the longest side straightly
= 9√15 m.
Wbbse Class 9 Area And Perimeter Of Triangle And Quadrilateral Important Questions Exercise 15.2
Question 10. The length of three sides of a triangular field of village of Paholampur are 26 meter, 25 meter and 30 meter.
1. Let us write by calculating what will be the cost of planting grass in the triangular field at the rate of Rs. 5 per sq. meter.
2. Let us write by calculating how much cost will be incurred for fencing around three sides at the rate of Rs. 18 per meter leaving a space 5 meter for constructing entrance gate of that triangular field.
Solution: Semi-perimeter of the triangular field = \(\frac{26+28+30}{2} m\)
=\(\frac{84}{2} m\)
= 42 m
Area of the field =
\(\begin{aligned}& =\sqrt{42(42-26)(42-28)(42-30)} \text { sq.m } \\
& \sqrt{42 \times 16 \times 14 \times 12} \text { sq.m } \\
& \sqrt{3 \times 14 \times 16 \times 14 \times 4 \times 3} \text { sq.m } \\
& 3 \times 14 \times 4 \times 2 \text { sq.m }=336 \text { sq.m }
\end{aligned}\)
1. Cost of planting grass in the field at the rate of Rs. 5 per sq.m Rs. 336 x 5 = Rs. 1680.
2. Perimeter of the field (26+28+30) m = 84 m
∴ Length of the fence = (84-5) m = 79 m
∴ Cost of fencing the garden, leaving 5 m for entrance gate at the rate of Rs. 18 per m. = Rs. 79 x 18 = Rs. 1422.
Question 11. Shakil draws an equilateral triangle PQR. I draw three perpendiculars from a point inside of that equilateral triangle on three sides, lengths of which are 10 cm, 12 cm and 8 cm. Let us write by calculating the area of the triangle.
Solution:
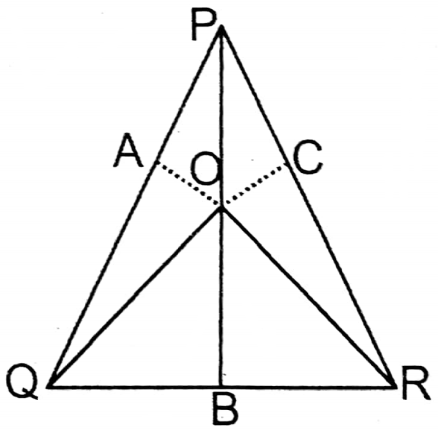
Given
Shakil draws an equilateral triangle PQR. I draw three perpendiculars from a point inside of that equilateral triangle on three sides, lengths of which are 10 cm, 12 cm and 8 cm.
Let each side of the equilateral triangle = a cm. OA, OB & OC are the perpendiculars drawn from O to the sides PQ, QR & RD respectively.
∴ OA = 10 m, OB = 12 m OC = 8 m
ΔPQR= ΔPOQ+ΔQOR+ΔPOR
\(or, \frac{\sqrt{3}}{4} a^2=\frac{1}{2} \times a \times 10+\frac{1}{2} \times a \times 12+\frac{1}{2} \times a \times 8\)or, \(\frac{\sqrt{3}}{4} a^2=5 a+6 a+4 a\)
or, \(\frac{\sqrt{3}}{4} a^2=15 a\)
or, \(\frac{\sqrt{3}}{4} a=15\)
\(or, a=\frac{60}{\sqrt{3}}or, a=\frac{60 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}=\frac{60 \sqrt{3}}{3}=20 \sqrt{3}\)
∴ Length of each side of the equilateral triangle = 20√3 m
∴ Area of equilateral triangle ΔPOR = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)
\(\begin{aligned}& =\frac{\sqrt{3}}{4} \times(20 \sqrt{3})^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 20 \sqrt{3} \times 20 \sqrt{3} \text { sq.cm } \\
& =300 \sqrt{3} \text { sq.cm. }
\end{aligned}\)
Question 12. The length of each equal side of an isosceles triangle is 20 m and the angle included between them is 45°. Let us write by calculating the area of the triangle.
Solution:
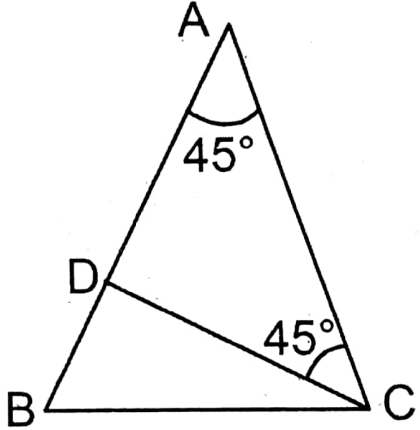
Given
The length of each equal side of an isosceles triangle is 20 m and the angle included between them is 45°.
Let ABC is an equilateral triangle whose AB = AC = 20 cm & ∠A = 45°.
Draw the perpendicular CD on AB.
In ΔABC, AB is the base & CD is perpendicular.
∠ACD = 45°
∴ AD = CD
In the right-angled triangle ΔADC,
AD2+CD2 =AC2
or, CD2+ CD2 = (20)2
or, 2CD2 =400
or, \(C D^2=\frac{400}{2}=200\)
or, \(C D=\sqrt{200}=10 \sqrt{2} \mathrm{~cm}\)
∴ Area of the triangle = \(\frac{1}{2} \times A B \times C D\)
\(\begin{aligned}& =\frac{1}{2} \times 20 \times 10 \sqrt{2} \text { sq.cm } \\
& =100 \sqrt{2} \text { sq.cm. }
\end{aligned}\)
Wbbse Class 9 Maths Area And Perimeter Exercise 15.2
Question 13. The length of each equal side of an isosceles triangle is 20 cm, and the angle included between them is 30°. Let us write by calculating the area of the triangle.
Solution:
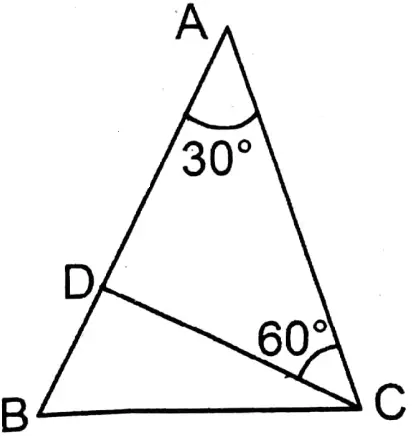
Given
The length of each equal side of an isosceles triangle is 20 cm, and the angle included between them is 30°.
Let ABC is an isosceles triangle whose AB = AC = 20 cm and ∠BAC = 30°. CD is the perpendicular on AB.
∴∠ACD = 60°
In right-angled ΔACD,
∠ACD = 2∠DAC
∴ \(C D=\frac{1}{2} A C=\frac{1}{2} \times 20 \mathrm{~cm}=10 \mathrm{~cm}\)
∴ Area of ΔABC = \(\frac{1}{2} \times A B \times C D\)
= \(\frac{1}{2} \times 20 \times 10 \text { sq.cm }\)
= 100sq.cm
Question 14. If the perimeter of an isosceles right-angled triangle is (√2+1)cm. Let us write by calculating the length of the hypotenuse and area of the triangle.
Solution: Let the length of the isosceles right angled triangle, length of equal side = a cm.
∴ Length of the hypotenuse = \(\sqrt{\mathrm{a}^2+\mathrm{a}^2} \mathrm{~cm}\)
\(\begin{aligned}& =\sqrt{2 \mathrm{a}^2} \mathrm{~cm} \\
& =\sqrt{2} \mathrm{a} \mathrm{cm}
\end{aligned}\)
∴ Perimeter of the triangle = (a+a+ √2 a) cm
= (2a + √2 a) cm
According to the problem, 2a+√2a = √2+1
or, \(a=\frac{\sqrt{2}+1}{2+\sqrt{2}}=\frac{(\sqrt{2}+1)}{\sqrt{2}(\sqrt{2}+1)}=\frac{1}{\sqrt{2}}\)
∴ Length of the hypotenuse = √2 a cm
= \(\sqrt{2} \times \frac{1}{\sqrt{2}} \mathrm{~cm}\)
= 1 cm
Area of the triangle = \(\frac{1}{2} \times a \times a\)
\(\begin{aligned}& =\frac{1}{2} \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}} \text { sq.cm } \\
& =\frac{1}{4} \text { sq.cm }
\end{aligned}\)
= 0.25 sq.cm.
Wbbse 9th Class Maths Area And Perimeter Exercise 15.2 Step By Step Solutions
Question 15. Maria cycling at a speed of 18 km per hour covers the perimeter of an equilateral triangular field in 10 minutes. Let us write by calculating the time required for Maria to go directly to the mid-point of the side of the field starting from its opposite vertex. (√3≈ 1.732)
Solution:
Given
Maria cycling at a speed of 18 km per hour covers the perimeter of an equilateral triangular field in 10 minutes.
Speed = 18 km/hr
Time 10 minutes = \(\frac{10}{60} \mathrm{hr}=\frac{1}{6} \mathrm{hr}\)
∴ Distance = speed x time = \(\)
= \(18 \times \frac{1}{6} \mathrm{~km}\) = 3 km
∴ Perimeter of triangular field = 3 km
∴ Length of each side of the field = \(\frac{3}{3} \mathrm{~km}\) = 1km
Height of the triangular field = \(\frac{\sqrt{3}}{2} \times(\text { side })\)
\(\begin{aligned}& =\frac{\sqrt{3}}{2} \times 1 \mathrm{~km} \\
& =\frac{\sqrt{3}}{2} \mathrm{~km}
\end{aligned}\)
∴ Time required to go from the vertex to the mid-point of the opposite side
\(\begin{aligned}& =\frac{\sqrt{3}}{2} \div 18 \mathrm{hr} \\
& =\frac{\sqrt{3}}{2} \times \frac{1}{18} \times 60 \text { minutes } \\
& =\frac{5 \sqrt{3}}{3} \text { minutes } \\
& =\frac{5 \times 1.732}{3} \text { minutes } \\
& =\frac{8.66}{3} \text { minutes }
\end{aligned}\)
= 2.89 minutes (approx)
Question 16. If the length of each side of an equilateral triangle is increased by 1 meter, then its area will be increased by √3 sq. meter. Let us write by calculating the length of a side of the equilateral triangle.
Solution:
Given
If the length of each side of an equilateral triangle is increased by 1 meter, then its area will be increased by √3 sq. meter.
Let each side of an equilateral side = a m.
∴ Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} a^2 \text { sq.m. }\)
It the length is increased by 1 m then new length = (a + 1) m.
∴ New area of the triangle = \(\frac{\sqrt{3}}{4}(a+1)^2 \text { sq.m }\)
According to the problem,
\(\frac{\sqrt{3}}{4}(a+1)^2=\frac{\sqrt{3}}{4} a^2+\sqrt{3}
or, \frac{\sqrt{3}}{4}(a+1)^2-\frac{\sqrt{3}}{4} a^2=\sqrt{3}\)
\(or, \frac{\sqrt{3}}{4}\left\{(a+1)^2-a^2\right\}=\sqrt{3}
or, \frac{\sqrt{3}}{4}\left(a^2+2 a+1-a^2\right)=\sqrt{3}\)
\(or, \frac{\sqrt{3}}{4}(2 a+1)=\sqrt{3}
or, 2 a+1=\sqrt{3} \times \frac{4}{\sqrt{3}}\)
or, 2a+1=4
or, 2a =4-1
or, 2a = 3
or, \(a=\frac{3}{2}\)
or, a = 1.5
∴ Each side of the equilateral triangle = 1.5 m.
Question 17. The area of an isosceles triangle and area of the square are in the ratio √3:2. If the length of the diagonal of the square is 60 cm, let us write by calculating the perimeter of the isosceles triangle.
Solution:
Given
The area of an isosceles triangle and area of the square are in the ratio √3:2. If the length of the diagonal of the square is 60 cm
Let each side of an equilateral triangle is a cm & each side of a square = x cm.
Length of the diagonal = \(\sqrt{\mathrm{x}^2+\mathrm{x}^2} \mathrm{~cm}\)
= \(=\sqrt{2 x^2} \mathrm{~cm}=x \sqrt{2} \mathrm{~cm}\)
According to the problem, x√2 = 60
or, x = \(\frac{60}{\sqrt{2}}=\frac{60 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}=\frac{60 \sqrt{2}}{2}\)
or, x = 30√√2
Again, according to the problem,
\(=\frac{\text { Area of the equilateral triangular }}{\text { Area of the square }}=\frac{\sqrt{3}}{2}\)\(or, \frac{\frac{\sqrt{3}}{4} a^2}{x^2}=\frac{\sqrt{3}}{2}\)
\(or, \frac{\sqrt{3} a^2}{4 x^2}=\frac{\sqrt{3}}{2}\)
or, a = √2.30√2 = 60
Length of each side of the equilateral triangle = 60 cm.
∴ And the perimeter of the triangle = 3 x 60 cm = 180 cm.
Wbbse Class 9 Maths Area And Perimeter Formulas With Examples Exercise 15.2
Question 18. Length of the hypotenuse and perimeter of a right-angled triangle is 13 cm and 30 cm. Let us write by calculating the area of a triangle.
Solution: Let the length of the sides containing the right angle of a right-angled triangle are a cm & b cm respectively.
∴ Length of the diagonal = \(\sqrt{a^2+b^2}\) and perimeter of the triangle
= \(a+b+\sqrt{a^2+b^2} \cdot c m\)
According to the 1st condition,
\(\begin{aligned}& \sqrt{a^2+b^2}=13 \\
& \text { or, }\left(\sqrt{a^2+b^2}\right)^2=(13)^2
\end{aligned}\)
(squaring both sides)
or, a2+b2 = 169 ….(1)
According to the 2nd condition,
a+b+ \(\sqrt{a^2+b^2}\) = 30
or, a+b+13=30
or, a+b=30-13
or, a + b = 17
(squaring both sides)
or, (a + b)2= (17)2
or, a2+ b2+2ab = 289
or, 169 +2ab = 289 (a2+ b2 = 169)
or, 2ab 289-169
or, 2ab = 120
or, \(a b=\frac{120}{2}\)
or, ab = 60
∴ Area of the right-angled triagle = \(\frac{1}{2} a b\)
= \(\frac{1}{2}\).60 sq.cm
= 30 sq. cm.
Question 19. The lengths of the sides containing the right angle are 12 cm and 5 cm. Let us write by calculating the length of the perpendicular drawn from the vertex of right angle on the hypotenuse.
Solution: Length of the hypotenuse of the right-angled triangle = \(\sqrt{(12)^2+(5)^2} \mathrm{~cm}\)
& =\sqrt{144+25} \mathrm{~cm} \\
& =\sqrt{169} \mathrm{~cm} \\
& =13 \mathrm{~cm}
\end{aligned}\)
Area of the right-angled triangle = \(\frac{1}{2}\)x12×5 = 30 sq.cm
∴ Length of the perpendicular drawn from the vertex of the right angle on the Hypotenuse
= \(\frac{2 x \text { Area of the triangular }}{\text { Length of the hypotenuse }}\)
\(\begin{aligned}& =\frac{2 \times 30}{13} \mathrm{~cm} \\
& =\frac{60}{13} \mathrm{~cm}
\end{aligned}\)
= 4.615 cm (Approx).
Question 20. The largest square is cut out from a right-angled triangular region with lengths of 3 cm, 4cm, and 5 cm respectively in such a way that one vertex of the square lies on the hypotenuse of the triangle. Let us write by calculating the length of a side of the square.
Solution:
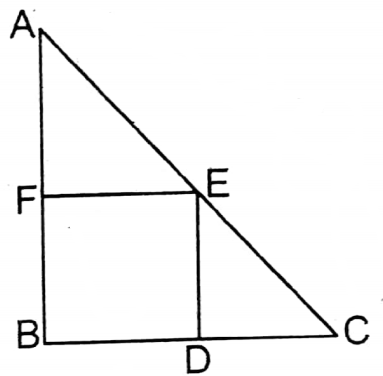
Let ABC is a right-angled triangle whose AB = 3 cm, BC= 4 cm, and length of the hypotenuse AC = 5 cm, and length of each side of the largest square which is cut from the triangle = a cm.
∴ AF (3-a) cm, CD = (4-a) cm
Area of ΔABC = \(\frac{1}{2}\) x ABxBC
= \(\frac{1}{2}\) x 3x 4 sq.cm
= 6 sq.cm
Area of ΔAFE= \(\frac{1}{2}\) × AF XFE
= \(\frac{1}{2}\) × (3 -a) xa sq.cm
Area of ΔCDE = \(\frac{1}{2}\)x CDx DE
= \(\frac{1}{2}\) x (4-a) x a sq.cm
Area of the square BDEF = ΔABC – (ΔAFE + ΔCDE)
or, \(a^2=6-\left\{\frac{1}{2}(3-a) \times a+\frac{1}{2}(4-a) \times a\right\}\)
or, \(a^2=6-\left(\frac{3 a-a^2+4 a-a^2}{2}\right)\)
or, \(a^2=6-\left(\frac{7 a-2 a^2}{2}\right)\)
or, 2a2 = 12-7a+2a2
or, 2a2-2a2+7a= 12
or, 7a = 12
or, a=1 \frac{5}{7}\)
Length of each side of the square= \(1 \frac{5}{7}\)
Question 21. Multiple choice questions
1. If each side of an equilateral triangle is 4 cm, the measure of height is
1. 4√3 cm
2. 16√3 cm
3. 8√3 cm
4. 2√3 cm
Solution: Height of equilateral triangle = \(\frac{\sqrt{3}}{2} \times(\text { side })\)
= \(\frac{\sqrt{3}}{2} \times 4 \mathrm{~cm}\)
= 2√3 cm
∴ 4. 2√3 cm
2. An isosceles right-angled triangle of which the length of each side of equal two sides is a unit. The perimeter of the triangle is
1. (1+ √2)a unit
2. (2+ √2)a unit
3. 3a unit
4.(3+2√2)a unit
Solution: Length of the hypotenuse of the right-angled isosceles triangle
\(\begin{aligned}& =\sqrt{a^2+a^2} \text { unit } \\
& =\sqrt{2 a^2} \text { unit }=\sqrt{2} \text { a unit }
\end{aligned}\)
= √2 a unit
∴ Perimeter of the triangle = a+a+√2 a unit
= 2a+√2 a unit
= (2+ √2)a unit
∴ 2. (2+√√2)a unit
3. If the area, perimeter, and height of an isosceles triangle are a, s, and h, then the value of \(\frac{2 a}{s h}\) is
1. 1
2. \(\frac{1}{2}\)
3. \(\frac{1}{3}\)
4. \(\frac{1}{4}\)
Solution: Let each side of an equilateral triangle = x unit.
Area of the equilateral triangle = (a) = \(\frac{\sqrt{3}}{4} x^2 \text { unit. }\)
The perimeter of the equilateral triangle (s) = 3x unit.
Height of the equilateral triangle =(h) = \(\frac{\sqrt{3}}{4} \times \text { unit. }\)
∴ \(\frac{2 a}{s h}=\frac{2 \cdot \frac{\sqrt{3}}{4} x^2}{3 x \cdot \frac{\sqrt{3}}{2} x}\)
or, \(\frac{2 a}{s h}=\frac{2 \sqrt{3}}{4} \times \frac{2}{3 \sqrt{3}}=\frac{1}{3}\)
∴ 3. \(\frac{1}{3}\)
4. The length of each equal side of an isosceles triangle is 5 cm and the length of base is 6 cm. The area of the triangle is
1. 18 sq. cm
2. 12 sq. cm.
3. 15 sq. cm
4. 30 sq. cm.
Solution: Area of the isosceles = \(\frac{1}{2} \times 6 \times \sqrt{(5)^2-\frac{(6)^2}{4}} \text { sq. cm. }\)
\(\begin{aligned}& =3 \sqrt{25-\frac{36}{4}} \text { sq. } \mathrm{cm} . \\
& =3 \sqrt{25-9} \text { sq. } \mathrm{cm} . \\
& =3 \times \sqrt{16} \text { sq. } \mathrm{cm} . \\
& =3 \times 4 \text { sq. } \mathrm{cm} . \\
& =12 \text { sq. } \mathrm{cm} .
\end{aligned}\)
∴ 2. 12 sq. cm
Class 9 Wbbse Area And Perimeter Of Triangle And Quadrilateral Exercise 15.2 Solved Exercises
5. D is such a point on AC of triangle ABC so the AD; DC = 3 : 2. If the area of triangle ABC is 40 sq. cm, the area of triangle BDC is
1. 16 sq. cm.
2. 24 sq. cm
3. 30 sq. cm.
4. 36 sq. cm
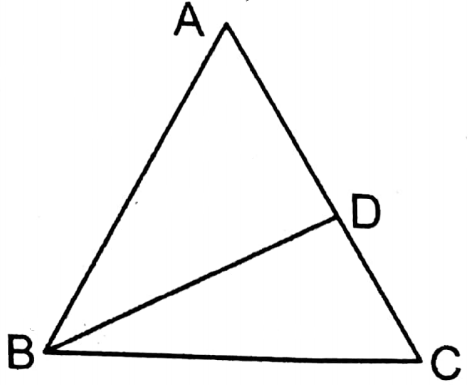
Solution: AD : DC = 3 : 2
or, \(\frac{A D}{D C}=\frac{3}{2}\)
or, \(\frac{\mathrm{AD}}{\mathrm{DC}}+1=\frac{3}{2}+1\)
or, \(\frac{A D+D C}{D C}=\frac{3+2}{2}\)
or, \(\frac{A C}{D C}=\frac{5}{2}\)
or, \(\frac{\triangle \mathrm{ABC}}{\triangle \mathrm{BDC}}=\frac{5}{2}\)
or, \(\frac{40 \text { sq. cm }}{\Delta \mathrm{BDC}}=\frac{5}{2}\)
or, area of = ΔBDC = \(\frac{80 \text { sq. cm }}{5}\)
∴ 1. 16 sq.cm
6. The difference of length of each side of a triangle from its semi- perimeter are 8 cm, 7 cm, and 5 cm respectively. The area of the triangle is
1. 20√7 sq. cm.
2. 10√14 sq. cm.
3. 20√14 sq. cm.
4. 140 sq. cm.
Solution: Let the length of 3 sides of the triangle be a cm, b cm & c cm.
∴ Perimeter of the triangle (2s) = a+b+c
According of the problem, sa 8, s-b7, s-c=5
∴ s-a+s-b+s-c=8+7+5
or, 3s (a+b+c) 20
or, 3s 2s 20
or, s = 20
∴ Area of the triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
\(\begin{aligned}& =\sqrt{20 \times 8 \times 7 \times 5} \text { sq.cm. } \\
& =\sqrt{4 \times 5 \times 4 \times 2 \times 7 \times 5} \text { sq. cm. } \\
& =4 \times 5 \sqrt{2 \times 7} \text { sq. cm. } \\
& =20 \sqrt{14} \text { sq. cm. }
\end{aligned}\)
∴ 3. 20√14 sq. cm.
Question 22. Short answer type questions
1. The numerical values of area and height of an equilateral triangle are equal. What is the length of a side of the triangle ?
Solution: Let each side of an equilateral triangle = a unit.
∴ Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} a^2 \text { sq. cm. }\)
∴ Height of the equilateral triangle \(\frac{\sqrt{3}}{2} a \text { sq. cm. }\)
According of the problem,
\(\frac{\sqrt{3}}{4} a^2=\frac{\sqrt{3}}{2} a
or, \frac{a}{2}=1
or, a=2\)
∴ Length of each side of the equilateral triangle = 2 unit.
2. If length of each side of an equilateral triangle is doubled, what percent of area will be increased of this triangle?
Solution: Let the 3 sides of a triangle are a unit, b unit, and c unit.
∴ Semi-perimeter of the triangle (s) = \(\frac{a+b+c}{2}\)
∴Area of the triangle (Δ) = \(\sqrt{s(s-a)(s-b)(s-c)}\)
If each side of the triangle be doubled,
Perimeter = 2a + 2b + 2c
= 2(a + b + c)
2(a+b+c)
∴ Semi-perimeter = \(\frac{2(a+b+c)}{2}\)
= a+b+c
= 2s
∴ Area of the new triangle = \(\sqrt{2 s(2 s-2 a)(2 s-2 b)(2 s-2 c)} \text { sq. cm }\)
\(\begin{aligned}& \sqrt{2 s \cdot 2(s-a) \cdot 2(s-b) \cdot 2(s-c)} \text { sq. } \mathrm{cm} \\
& 4 \sqrt{s(s-a)(s-b)(s-c)} \text { sq. cm }
\end{aligned}\)
= 4Δ
∴ Percentage of increased area = \(\frac{4 \Delta-\Delta}{\Delta} \times 100 \%=300 \%\)
3. If the length of each side of an equilateral triangle is trippled, what percent of area will be increased of this triangle ?
Solution: Let the 3 sides of a triangle are a unit, b unit & c unit.
∴ Area of triangle = (Δ) = \(\sqrt{s(s-a)(s-b)(s-c)} \text { sq. } \mathrm{cm}\)
If each side of the triangle be trippled = \(\sqrt{3 s .3(s-a) 3(s-b) 3(s-c)} \text { sq. } \mathrm{cm}\)
New area = 9Δ
∴ Percentage of increased area = \(\frac{9 \Delta-\Delta}{\Delta} \times 100 \%=800 \%\)
4. The lengths of sides of a right-angled triangle are (x-2) cm, x cm and (x+2) cm. How much is the length of hypotenuse ?
Solution: As the hypotenuse of an right angle triangle is the biggest side,
∴ Length of the hypotenuse = (x+2) cm
According to Pythagoras’ theorem,
(x + 2)2= (x)2 +(x-2)2
or, x2 + 4x + 4 = x2 + x2 – 4x + 4
or, x2-8x=0
or, x(x-8)=0
or, x = 0 and x-8=0
If x-8=0 or x = 8 , x = 0, 8
but x ≠ 0
X = 8
∴ Length of the hypotenuse = (8 + 2) cm = 10 cm.
5. A square is drawn on the height of a equilateral triangle. What is the ratio of areas of triangle and square?
Solution: Let the each side of an equilateral triangle = a unit.
∴ Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} a^2\)
Height of the equilateral triangle = \(\frac{\sqrt{3}}{2} \text { a unit. }\)
∴ Area of the square drawn on the height of the triangle = \(\left(\frac{\sqrt{3}}{2} a\right)^2 \text { sq.unit }\)
= \(\frac{3 a^2}{4} \text { sq.unit }\)
∴ Ratio of area of the triangle & the area of square= \(\frac{\sqrt{3}}{4} a^2: \frac{3 a^2}{4}\)= √3:3
= √3:√3.√3 =1:√3
