WBBSE Solutions For Class 9 Maths Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.3

Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.3

Question 1. Ratul draws a parallelogram with a length of base 5 cm and a height 4 cm. Let us calculate the area of the parallelogram drawn by Ratul.

Solution:

Given

Ratul draws a parallelogram with a length of base 5 cm and a height 4 cm.

Area of parallelogram = base x height
= 5 x 4 sq. cm
= 20 sq. cm

Question 2. The base of a parallelogram is twice its height. If the area of shape of a parallelogram is 98 sq. cm, then let us calculate the length and height of the parallelogram.

Solution:

Given

The base of a parallelogram is twice its height. If the area of shape of a parallelogram is 98 sq. cm

Let the height of a parallelogram = x cm.
∴ Base of the parallelogram = 2x cm.

∴ Area of parallelogram = base x height
= 2x.x sq. cm
= 2x² sq. cm

Read and Learn More WBBSE Solutions For Class 9 Maths

According to the problem, 2x² = 98

or, x² = 98
or, x² = 49
or, x = √49
or, x = 7

∴ Height of the parallelogram = 7 cm.
∴ Base of the parallelogram = 2 x 7 cm = 14 cm.

Question 3. There is a shape of parallelogram land beside our house, with lengths of adjacent sides of which are 15 meters and 13 meters. If the length of one diagonal is 14 meters, then let us calculate the area of shape of parallelogram land.

Solution:

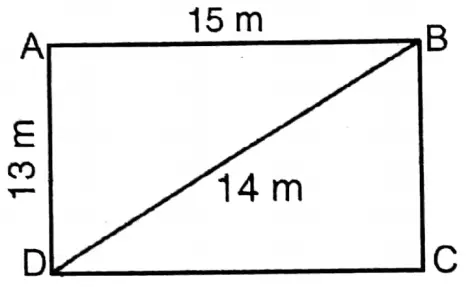
Given

There is a shape of parallelogram land beside our house, with lengths of adjacent sides of which are 15 meters and 13 meters. If the length of one diagonal is 14 meters,

Let ABCD is a parallelogram whose = AB = DC = 15 m
AD = BC = 13 m
Diagonal BD = 14 meter

Semi-perimeter ΔABD (s) = \(\frac{13+14+15}{2} m\)

= \(\frac{42}{2}\) m = 21 m

Area of ΔABD = \(\sqrt{21(21-13)(21-14)(21-15)} \text { sq. cm }\)

= \(\sqrt{21 \times 8 \times 7 \times 6} \text { sq. cm }\)

= \(\sqrt{3 \times 7 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3} \text { sq. cm }\)

= 2 × 2 × 3 × 7 sq. cm
= 84 sq. cm

∴ The diagonal divides the parallelogram in two equal triangles.

∴ Area of parallelogram □ABCD = 2xΔABD
= 2 × 84 sq. m
= 168 sq. m

Question 4. Pritha drew a parallelogram, adjacent sides of which are 25 cm and 15 cm, and length of one diagonal is 20 cm. Let us write by calculating the height of the parallelogram which is drawn on the side of 25 cm.

Solution:

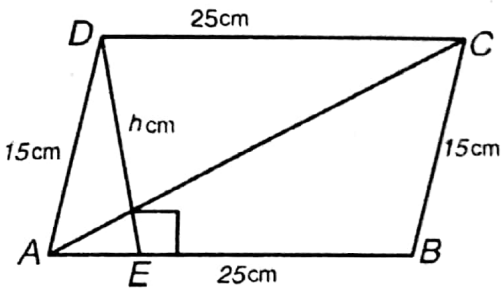
Given

Pritha drew a parallelogram, adjacent sides of which are 25 cm and 15 cm, and length of one diagonal is 20 cm.

Let ABCD is a parallelogram whose = AB = DC = 25 cm
AD = BC= 15 cm

and diagonal = AC = 20 cm

Semi-perimeter of ΔABC (s) = \(\frac{25+15+20}{2} \mathrm{~cm}\)

= \(\frac{60}{2} \mathrm{~cm}=30 \mathrm{~cm}\)

∴ Area of ΔABC = \(\sqrt{30(30-25)(30-15)(30-20)} \text { sq.cm }\)

= \(\sqrt{30 \times 5 \times 15 \times 10} \text { sq.cm }\)

= \(\sqrt{2 \times 3 \times 5 \times 5 \times 3 \times 5 \times 2 \times 5} \text { sq.cm }\)

=2x 3 x 5 x 5 sq.cm =150 sq.cm

∴ Area of □ABCD = 2x ΔABC
= 2 × 150 sq.cm
= 300 sq.cm

Length of the perpendicular drawn from D on AB = H cm

∴ Area of parallelogram □ABCD = base x height = 25 x h sq.cm

According to the problem, 25h=300

or, h = \(\frac{300}{25}\)

or, h = 12

∴ Height of the parallelogram drawn on the side of length 25 cm from the opposite vertex = 12 cm.

Question 5. The lengths of two adjacent sides are 15 cm and 12 cm of a parallelogram; the distance between two smaller sides is 7.5 cm. Let us calculate the distance between the two sides.

Solution:

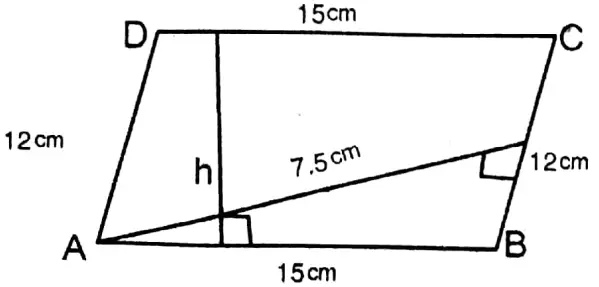
Given

The lengths of two adjacent sides are 15 cm and 12 cm of a parallelogram; the distance between two smaller sides is 7.5 cm.

Let ABCD is a parallelogram whose larger side AB = DC = 15 cm and smaller side BC = AD = 12 cm.

Distance between two smaller sides = 7.5 cm and let the distance between two bigger sides = h cm.

Area of parallelogram □ABCD base x height
= 12 x 7.5 sq. cm
= 90 sq.cm

Again, area of the parallelogram ABCD base x height
= AB × h
= 15 x h sq. cm
= 15h sq. cm

According to the problem,15h = 90

or, h= \(\frac{90}{15}\) = 6

∴ Distance between two longer sides = 6 cm.

Question 6. If the measure of two diagonals of a rhombus are 15 meters and 20 meters, then let us write by calculating its perimeter, area, and height.

Solution:

 

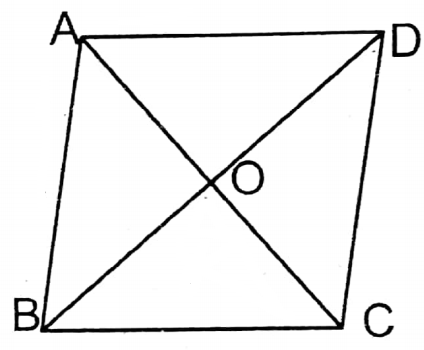
Let ABCD is a rhombus whose diagonals AC & BD intersect at O & AC = 15 m and BD = 20 m.

∴ We know the diagonals of a rhombus bisect each other perpendicularly.

∴ AO = OC = \(\frac{15}{2}\)

and BO = OD= \(\frac{20}{2}\) m = 10 m

In right angled ΔBOC,

BC = \(\sqrt{O B^2+O C^2}\)

= \(\sqrt{\left(\frac{15}{2}\right)^2+(10)^2}\)

= \(\sqrt{\frac{225}{4}+100}\)

= \(\sqrt{\frac{225+400}{4}}\)

= \(\sqrt{\frac{625}{4}}\)

= \(\frac{25}{2} \mathrm{~m}\)

∴ Perimeter of the Rhombus = 4 x side

= \(4 \times \frac{25}{2}\)m

= 50 m

Area of rhombus = \(\frac{1}{2}\) x product of the diagonals

= \(\frac{1}{2}\) x 15 × 20 sq.m = 150 sq.m

Base x height = Area of the rhombus

∴ \(\frac{25}{2}\)x height = 150

or, height = \(\frac{150 \times 2}{25}\) m = 12 m.

Question 7. If the perimeter of a rhombus is 440 meters and the distance between two parallel sides is 22 meters, let us write by calculating the area of the rhombus.

Solution: Perimeter of rhombus = 440 m

∴ Length of each side of the rhombus = \(\frac{440}{4}\) m = 110m

Area of rhombus = base x height
= 110 x 22 sq.m
= 2420 sq.m

Question 8. If perimeter of the rhombus is 20 cm and the length of its diagonal is 6 cm, then let us write by calculating the area of the rhombus.

Solution: Perimeter of rhombus = 20 cm.

∴ Length of one side of the rhombus = \(\frac{440}{4}\) cm = 5 cm.

Length of the diagonal = 6 cm & diagonals AC & BD intersect each other at O.

∴ OA = \(\frac{6}{2}\) cm = 3 cm and AB = 5 cm

In right-angled ΔAOB

OA²+ OB² = AB²
or, (3)²+ OB²= (5)²
or, OB² = 25-9
or, OB²= 16
or, OB = √16 =4

∴ 2nd diagonal of the rhombus = BD = 2 x OB = 2 x 4 cm = 8 cm.

∴ Area of the rhombus = \(\frac{1}{2}\) x product of the diagonals

= \(\frac{1}{2}\) x 6 x 8 sq.cm = 24 sq.cm.

Question 9. The area of field shaped in trapezium is 1400 sq. dcm. If the perpendicular distance between two parallel sides are 20 dcm and the length of two parallel sides is in the ratio 3: 4, then let us write by calculating the lengths of two sides.

Solution:

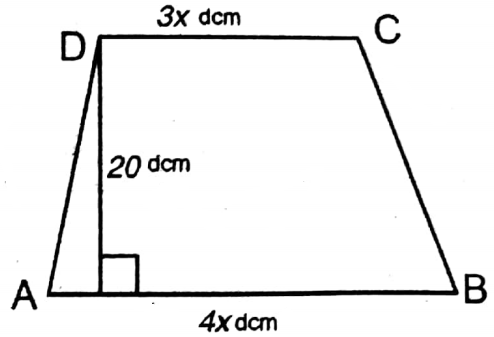
Given

The area of field shaped in trapezium is 1400 sq. dcm. If the perpendicular distance between two parallel sides are 20 dcm and the length of two parallel sides is in the ratio 3: 4

Let the lengths of the parallel sides of the trapezium be 3x dm & 4x dm.

Area of the trapezium = \(\frac{1}{2}\) x (3x+4x) x 20 sq.dcm = 70x sq.dcm

According to the problem, 70x = 1400

or, x = \(\frac{1400}{70}\) = 20

∴ Length of 1st side = 3 x 20 dm = 60 dm
& length of 2nd side = 4 x 20 dm = 80 dm.

Question 10. Let us write by calculating the area of a regular hexagon field whose length of sides is 8 cm.

[Hints: If we draw diagonals, we get equal six equilateral triangles]

Solution:

 

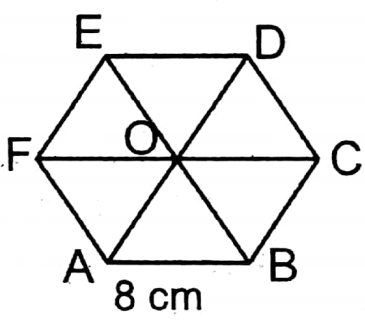
By joining the diagonals of a regular hexagon six equilateral triangles are formed.

∴ Area of the regular hexagon = 6 x Area of six equilateral triangles

= 6 x \(\frac{\sqrt{3}}{4}\) x (8)² sq. cm

=6 x \(\frac{\sqrt{3}}{4}\) x 64 sq. cm

= 96√3 sq. cm

Question 11. In a quadrilateral ABCD, AB = 5 meters, BC = 12 meters, CD = 14 meters, DA = 15 meters, and ∠ABC = 90°, let us write by calculating the area of the quadrilateral shape of the field.

Solution:

 

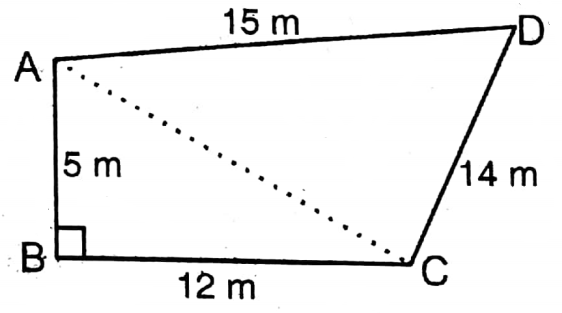
In quadrilateral ABCD, AB = 5 m, BC = 1 m, CD = 14 m, DA = 15 m and ∠ABC = 90°
AC is the diagonal.

In a right-angled triangle ΔABC,

AC²= AB² + BC²
or, AC² = (5)² + (12)²
or, AC² = 25+144

or, AC²= 169
or, AC = √169
or, AC = 13

Area of right-angled triangle ΔABC = \(\frac{1}{2}\) X AB X BC

= \(\frac{1}{2}\)  x 5×12 sq.cm = 30 sq. cms

Semi-perimeter of ΔACD (s) = \(\frac{13+14+15}{2}\)

= \(\frac{42}{2}\) m = 21 m

Area of ΔACD = \(\sqrt{s(s-a)(s-b)(s-c)}\)

= \(\sqrt{21(21-13)(21-14)(21-15)} \text { sq.m }\)

= \(\sqrt{21 \times 8 \times 7 \times 6} \text { sq.m }\)

= \(\sqrt{3 \times 7 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3} \text { sq.m }\)

= 2 x 2 x 3 x 7 sq.m
= 84 sq.m

Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= 30 sq.m +84 sq.m
= 114 sq.m

Question 12. Sahin draws a trapezium ABCD whose length of diagonal BD is 11 cm and draws two perpendiculars whose lengths are 5 cm and 11 cm respectively from points A and C on the diagonal BD. Let us write by calculating the area of ABCD of the trapezium.

Solution:

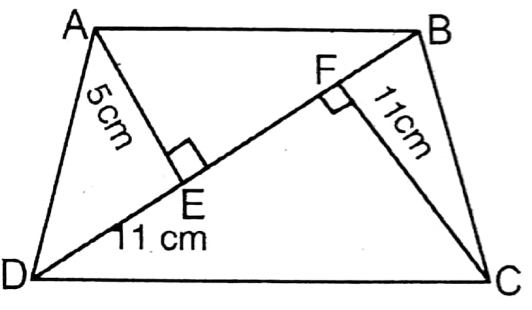
Given

Sahin draws a trapezium ABCD whose length of diagonal BD is 11 cm and draws two perpendiculars whose lengths are 5 cm and 11 cm respectively from points A and C on the diagonal BD.

ABCD is a trapezium on the diagonal BD, AE & CF are the perpendiculars drawn from A & C respectively, AE = 5 cm & CF = 11 cm.

Area of trapezium ABCD = area of ΔABD + area of ΔBCD

= \(\frac{1}{2}\) x BD X AE+ \(\frac{1}{2}\) x BD X CF

= \(\frac{1}{2}\) x BD(AE+CF)

= \(\frac{1}{2}\) x 11(5+11) sq.cm

= \(\frac{1}{2}\)x11x16 sq.cm = 88 sq.cm.

Question 13. ABCDE is a pentagon whose side BC is parallel to diagonal AD, EP is perpendicular on BC, and EP intersects AD at the point Q. BC= 7 cm, AD = 13 cm, PE = 9 cm, and if PQ=\(\frac{4}{9}\) PE, let us write by calculating the area of ABCD: pentagon.

Solution:

 

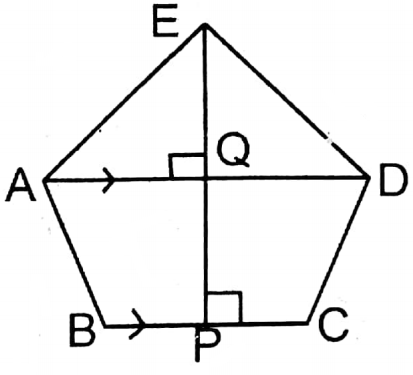
In pentagon ABCDE, BC II AD & EP ⊥ BC and EP cuts AD at Q. BC= 7 cm, AD 13 cm, PE = 9 cm

PQ = \(\frac{4}{9}\) PE = \(\frac{4}{9}\) X 9 cm = 4 cm

EQ=PE-PQ (9-4) cm = 5 cm

Area of ΔAED = \(\frac{1}{2}\) x ADXEQ

= \(\frac{1}{2}\)x13x5 sq.cm

= \(\frac{65}{2}\)sq.cm = 32.5 sq.cm

Area of trapezium ABCD = \(\frac{1}{2}\) (AD+BC) x PQ

= \(\frac{1}{2}\) (13+7)x4 sq.cm = 40 sq.cm

Area of pentagon ABCDE = Area ΔAED + Area of trapezium ΔBCD
=(32.5+40) sq.cm
= 72.5 sq.cm.

Question 14. The length of a rhombus is equal to the length of a square and the length of a diagonal of the square is 40√2 cm. If the lengths of diagonals of a rhombus are in the ratio 3: 4, then let us write by calculating the area of a field in the shape of the rhombus.

Solution:

 

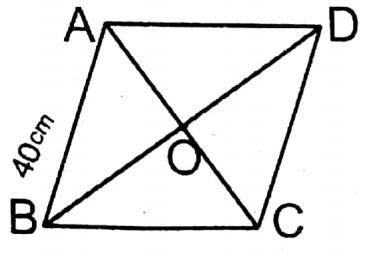
Length of the diagonal of square = 40√2 cm.

∴ Length of one side of the square = \(\frac{40 \sqrt{2}}{\sqrt{2}}\) cm = 40 cm.

∴ Length of one side of the rhombus = 40 cm.

Diagonals AC & BD of the rhombus ABCD bisect each other at O; and AC = 3x cm and BD = 4x cm & AB = 40 cm.

∴ AO = OC= \(\frac{3 x}{2}\)cm

BO = OD = \(\frac{4x}{2}\) cm = 2x cm

In the right-angled triangle ΔAOB, AO²+ BO² = AB²

or, \(\left(\frac{3 x}{2}\right)^2\) + (2x)² = (40)²

or,\(\frac{9 x^2}{4}+4 x^2=1600\)

or, \(\frac{9 x^2+16 x^2}{4}=1600\)

or, 25x²= 6400

or, \(x^2=\frac{6400}{25}\)

or, x² = 256
or, x= √256 = 16

∴ Length of one diagonal of the rhombus = 3 x 16 cm = 48 cm
& the length of the 2nd diagonal = 4 x 16 cm = 64 cm.

∴ Area of the rhombus = \(\frac{1}{2}\) x product of the diagonals

= \(\frac{1}{2}\) x 48 x 64 sq.cm
= 1536 sq.cm.

Question 15. In a trapezium, the length of each slant side is 10 cm and the length of the parallel sides are 5 cm and 7 cm respectively. Let us write by calculating the area of the field in the shape of the trapezium and its diagonal.

Solution:

 

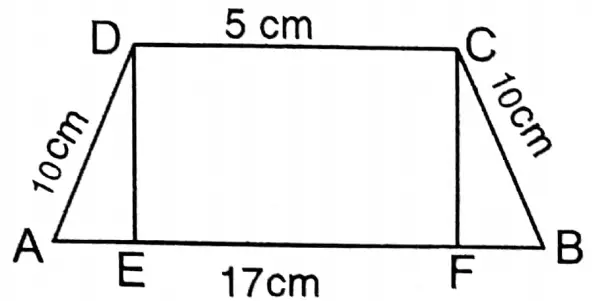
Let ABCD is an isosceles trapezium whose each slant side: AD = BC = 10 cm, CD = 5 cm, and AB = 17 cm. DF and CF are the perpendiculars drawn on AB from D and C.

∴ DC EF = 5 cm

ΔAED and ΔCFB are congruent triangles.
∴ AE = FB = 6 cm

In right-angled ΔAED,
DE²= AD² – AE²
or, DE²= 100-36
or, DE² = 64
or, DE = √64 = 8

∴ Area of trapezium ABCD = \(\frac{1}{2}\)(5+17)x8 sq.cm

= \(\frac{1}{2}\) x 22 x 8 sq.cm = 88 sq.cm

Join A, C

In right-angled ΔAFC,
AC²= AF²+ CF²
or, AC²= (11)² + (8)²
or, AC² =121 +64
or, AC²= 185
or, AC = √185

The diagonal of the trapezium is √185 cm & its area is 88 sq. cm.

Question 16. The lengths of the parallel sides of a trapezium are 19 cm and 9 cm and the length of the slant sides are 8 cm and 6 cm. Let us calculate the area of the field in the shape of a trapezium.

Solution:

 

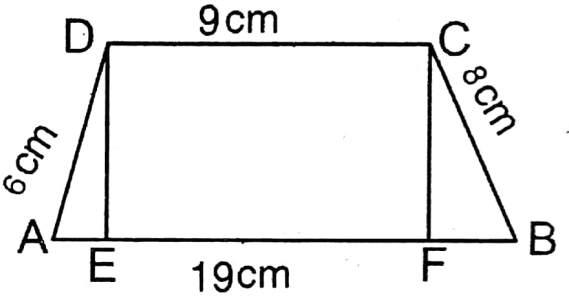
Let the length of the slant sides AD & BC of the trapezium are 6 cm & 8 cm respectively and the lengths of AB & CD be 19 cm & 9 cm respectively.
DE and CF are the perpendiculars on AB from D & C respectively.

Let DE = CF = h cm

In right-angled ΔAED, \(A E=\sqrt{A D^2-D E^2}\)

\(\begin{aligned}
& \sqrt{(6)^2-h^2} \\
& \sqrt{36-h^2}
\end{aligned}\)

In right-angled ΕCFB, FB = \(\sqrt{B C^2-C F^2}\)

\(\begin{aligned}
& \sqrt{(8)^2-h^2} \\
& \sqrt{64-h^2}
\end{aligned}\)

∴ AE+ EF + FB = 19

∴ \(\sqrt{36-h^2}\) +9+\(\sqrt{64-h^2}\)= 19

or, \(\sqrt{36-h^2}\)=19-9-\(\sqrt{64-h^2}\)

or, \(\sqrt{36-h^2}\)=10-\(\sqrt{64-h^2}\)]

or, \(\left(\sqrt{36-h^2}\right)^2=\left(10-\sqrt{64-h^2}\right)^2\) (squaring both sides)

or, 36-h² = 100+ 64-h²-20\(\sqrt{64-h^2}\)

or, 20\(\sqrt{64-h^2}\) = 164-36+ h² – h²

or, 20\(\sqrt{64-h^2}\) = 128

or, \(\sqrt{64-h^2}=\frac{128}{20}\)

or, \(\sqrt{64-h^2}\) = 6.4

or, \(\left(\sqrt{64-h^2}\right)^2=(6.4)^2\)

(squaring both sides)

or, 64 – h² = 40.96
or, -h² = 40.96-64
or, -h² = -23.04
or, h²=23.04

or, h= \(\sqrt{23.04}\) = 4.8

∴ Height of the trapezium = 4.8 cm

∴ Area of the trapezium = \(\frac{1}{2}\) (19+9) x 4.8 sq.cm

= \(\frac{1}{2}\) x 28 x 4.8 sq.cm
= 67.2 sq.cm.

Question 17. Multiple choice question

1. The height of a parallelogram is \(\frac{1}{3}\)th of its base. If the area of the field is 192 sq. cm in the shape of a parallelogram, the height is

1. 4 cm
2. 8 cm
3. 16 cm.
4. 24 cm

Solution: Let the base of a parallelogram = x cm

∴ Height of the parallelogram = \(\frac{x}{3}\) cm

∴ Area of the parallelogram = base x height

= X. \(\frac{x}{3}\)  sq.cm

= \(\frac{x^2}{3}\) sq. cm

According to the problem, \(\frac{x^2}{3}\)= 192

or, x² = 576
or, x= √576 = 24

∴ Height of the parallelogram = \(\frac{24}{3}\) = 8cm

∴ 2. 8 cm

2.  If the length of one side of a rhombus is 6 cm and one angle is 60°, then the area of field in the shape of a rhombus is

1. 9√3 sq. cm
2. 18/3 sq. cm
3. 36√3 sq. cm
4. 6√3 sq. cm

 

 

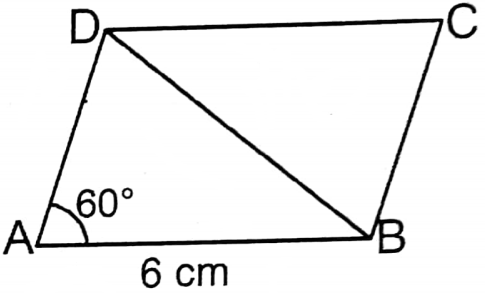
Solution: Let ABCD is a rhombus whose side AB = 6 cm and ∠BAD = 60°.

In ΔABD,
AB = AD (all the sides of the rhombus are equal)

∴ ∠ADB = ∠ABD = 60°
∴ ΔABD is an equilateral triangle whose each side = 6 cm.

∴ Area of ΔABD= \(\frac{\sqrt{3}}{4} \times(6)^2\) sq.cm

= \(\frac{\sqrt{3}}{4}\) x 36 sq.cm = 9√3 sq. cm

Similarly, area of ΔBCD = 9√3 sq.cm

∴ Area of rhombus = Area ΔABD + Area ΕBCD

= (9/3+9√3) sq.cm
=18√3 sq.cm

∴ 2. 18√3 sq. cm

3. The length of one diagonal of a rhombus is thrice of its the other diagonal. If the area of the field in the shape of a rhombus is 96 sq. cm, then the length of the longer diagonal is

1. 4 cm
2. 12 cm
3. 16 cm
4. 24 cm

Solution: Let one diagonal of rhombus = x cm
∴ Length of 2nd diagonal = 3x cm.

∴ Area of rhombus = \(\frac{1}{2}\).x.3x sq.cm

= \(\frac{3 x^2}{2}\) cm

According to the problem,

\(\frac{3 x^2}{2}\) = 96

or, \(x^2=\frac{96 \times 2}{3}\)

or, x² = 64
or, x = √64 = 8

∴ Length of the longer diagonal = 3 x 8 cm = 24 cm.

∴ 4. 24 cm

4. A rhombus and a square are on the same base. If the area of the square is x2 sq. unit and the area of the field in the shape of a rhombus is y sq. unit. then

1.  y > x
2. y < x²
3. y = x²
4. y = 2x²

 

 

Solution: The lengths of the base of a rhombus and a square are the same.

∴ Area of the square is greater than the area of the rhombus as the height of the square is greater than the height of the rhombus.

∴ x² > y

∴ 2.  y < x

5. Area of a field in the shape of the trapezium is 162 sq. cm and the height is 6 cm. If the length of one side is 23 cm, then the length of the other side is

1. 29 cm
2. 31 cm
3. 32 cm
4. 33 cm

Solution: Let the other side of the parallelogram = x cm

∴ Area of trapezium = \(\frac{1}{2}\) (23+x) x6 sq.cm
= 3(23+x) sq.cm

According to the problem, 3(23+x) = 162

or, 23 + x = \(\frac{162}{3}\)

or, 23+ x = 54
or, x = 54-23
or, x = 31

∴ Length of 2nd side of the trapezium = 31 cm.

∴ 2. 31 cm

Question 18. Short answer type questions

1. Area of the field in the shape of parallelogram ABCD is 96 sq. cm, length of diagonal BD is 12 cm. What is the perpendicular length drawn on diagonal BD from point A?

Solution:

 

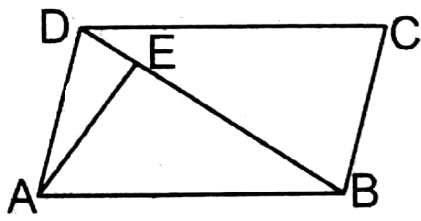
Let AE is the perpendicular from A on the diagonal BD of the parallelogram ABCD.

∴ Diagonal bisects the parallelogram in two equal triangles.

∴ Area of ΔABD= \(\frac{1}{2}\) x Area of the parallelogram ABCD

or, \(\frac{1}{2}\) x BDX AE = \(\frac{1}{2}\) x 96 sq.cm

or, \(\frac{1}{2}\) x 12 x AE= 48 sq.cm

or, AE = \(\frac{48}{6}\) = 8cm

∴ Perpendicular length from A on the diagonal BD = 8 cm.

2. Length of the height of the rhombus is 14 cm and the length of the side is 5 cm. What is the area of the field in the shape of a rhombus?

Solution:

 

Let ABCD is a parallelogram whose AB = DC = 5 cm and BC = AD = 3 cm. Distance between two greater sides AB & DC= 2 cm.

∴ Area of parallelogram □ =base x height
= 5 x 2 sq. cm
= 10.sq.cm

Let the distance between AD & BC of the parallelogram = h cm.

∴ Area of parallelogram □ABCD base x height
= BC x h
= 3 × h sq. cm

According to the problem,
3h = 10

or, h= \(\frac{10}{3:}=3 \frac{1}{3}\)

The distance between two smaller sides = \(3 \frac{1}{3}\)

3. Length of the height of the rhombus is 14 cm and the length of each side is 5 cm. What is the area of the field in the shape of a rhombus?

Solution: Area of Rhombus = base x height
= 5 x 14 sq. cm
= 70 sq. cm

4. Any adjacent parallel sides of a trapezium make an angle 45° and the length of its slant side is 62 cm, what is the distance between its two parallel sides?

Solve: Let ABCD is an isoceles trapezium whose : AD = BC= 62 cm and ∠DAB = 45°.
DE is the perpendicular from D on AB.

∴ ∠AED = 90°
∴ ∠ADE 180°-(90°+45°) = 45°

In ΔADE ∠DAE = ∠ADE
∴ AE = DE = h (let)

In right-angled ΔAED
AE²+ DE² = AD²
or, h² + h² = (62)²
or, 2h² = 62 × 62

or, \(h^2=\frac{62 \times 62}{2}\)\

or, h²= 31 x 62
or, h= √31×62
or, h = √31x31x2
or, h= 31√2

∴ Distance between the parallel sides = 31√2 cm.

5. In parallelogram ABCD, AB = 4 cm, BC = 6 cm, and ∠ABC = 30°, find the area of the field in the shape of parallelogram ABCD.

Solution:

 

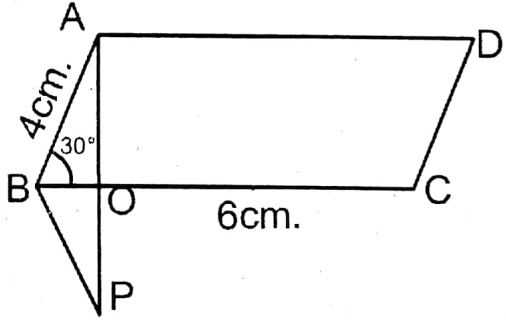
In parallelogram, ABCD, AB = 4 cm, BC = 6 cm and ∠ABC = 30°.

AO is the perpendicular from A on BC, AO produced such that AO = OP.

In ΔAOB and ABOP, AO = OP (By construction)
and BO is common and ∠AOB = ∠POB ( each = 90°)

∴ ΔAOB≅ΔBOP (S-A-S condition)

∴ AB = BP & ZABO ZPBO = 30°
In ΔABP ∠ABP = ∠BAP = ∠BPA = 60°

∴ΔABP is an equilateral triangle.
∴AP AB = 4 cm

∴ \(A O=\frac{1}{2} A P=\frac{1}{2} A B=\frac{1}{2} \times 4 \mathrm{~cm}=2 \mathrm{~cm}\)

Area of ABCD parallelogram = Base x Height
= BC × AO
= 6 x 2 sq.cm
= 12 sq.cm